常见的C/C++开源QP问题求解器
1. qpSWIFT
qpSWIFT 是面向嵌入式和机器人应用的轻量级稀疏二次规划求解器。它采用带有 Mehrotra Predictor 校正步骤和 Nesterov Todd 缩放的 Primal-Dual Interioir Point 方法。
- 开发语言:C
- 文档:传送门
- 项目:传送门
2. OSQP
OSQP(算子分裂二次规划)求解器是一个数值优化包,用于求解以下形式的凸二次规划:
m i n i m i z e 1 2 x T P x + q T x s u b j e c t t o l ≤ A x ≤ u \begin{aligned}&\mathrm{minimize}\quad\frac12x^TPx+q^Tx\\&\mathrm{subject~to}\quad l\leq Ax\leq u\end{aligned} minimize21xTPx+qTxsubject tol≤Ax≤u
- 开发语言:C
- 文档:传送门
- 项目:传送门,另一个简单Eigen-C++封装项目
3. qpOASES
Open-source C++ implementation of the recently proposed online active set strategy
- 开发语言:C++
- 文档:传送门
- 项目:传送门
参考链接:
- https://zhuanlan.zhihu.com/p/464676135
相关文章:

常见的C/C++开源QP问题求解器
1. qpSWIFT qpSWIFT 是面向嵌入式和机器人应用的轻量级稀疏二次规划求解器。它采用带有 Mehrotra Predictor 校正步骤和 Nesterov Todd 缩放的 Primal-Dual Interioir Point 方法。 开发语言:C文档:传送门项目:传送门 2. OSQP OSQP&#…...

前端axios发送请求,在请求头添加参数
1.在封装接口传参时,定义形参,params是正常传参,name则是我想要在请求头传参 export function getCurlList (params, name) {return request({url: ********,method: get,params,name}) } 2.接口调用 const res await getCurlList(params,…...

CTF Misc(3)流量分析基础以及原理
前言 流量分析在ctf比赛中也是常见的题目,参赛者通常会收到一个网络数据包的数据集,这些数据包记录了网络通信的内容和细节。参赛者的任务是通过分析这些数据包,识别出有用的信息,例如登录凭据、加密算法、漏洞利用等等 工具安装…...

Telink泰凌微TLSR8258蓝牙开发笔记(二)
在开发过程中遇到了以下问题,记录一下 1.在与ios手机连接后,手机app使能notify,设备与手机通过write和notify进行数据交换,但是在连接传输数据一端时间后,设备收到write命令后不能发出notify命令,打印错误…...
vue3+elementPlus:el-tree复制粘贴数据功能,并且有弹窗组件
在tree控件里添加contextmenu属性表示右键点击事件。 因右键自定义菜单事件需要获取当前点击的位置,所以此处绑定动态样式来控制菜单实时跟踪鼠标右键点击位置。 //html <div class"box-list"><el-tree ref"treeRef" node-key"id…...

JTS:10 Crosses
这里写目录标题 版本点与线点与面线与面线与线 版本 org.locationtech.jts:jts-core:1.19.0 链接: github public class GeometryCrosses {private final GeometryFactory geometryFactory new GeometryFactory();private static final Logger LOGGER LoggerFactory.getLog…...

MySQL中的SHOW FULL PROCESSLIST命令
在MySQL数据库管理中,理解和监控当前正在执行的进程是至关重要的一环。MySQL提供了一系列强大的工具和命令,使得这项任务变得相对容易。其中,SHOW FULL PROCESSLIST命令就是一个非常有用的工具,它可以帮助我们查看MySQL服务器中的…...

VsCode 常见的配置、常用好用插件
1、自动保存:不用装插件,在VsCode中设置一下就行 2、设置ctr滚轮改变字体大小 3、设置选项卡多行展示 这样打开了很多个文件,就不会导致有的打开的文件被隐藏 4、实时刷新网页的插件:LiveServer 5、open in browser 支持快捷键…...

深度学习问答题(更新中)
1. 各个激活函数的优缺点? 2. 为什么ReLU常用于神经网络的激活函数? 在前向传播和反向传播过程中,ReLU相比于Sigmoid等激活函数计算量小;避免梯度消失问题。对于深层网络,Sigmoid函数反向传播时,很容易就…...

JavaScript 笔记: 函数
1 函数声明 2 函数表达式 2.1 函数表达式作为property的value 3 箭头函数 4 构造函数创建函数(不推荐) 5 function 与object 5.1 typeof 5.2 object的操作也适用于function 5.3 区别于⼀般object的⼀个核⼼特征 6 回调函数 callback 7 利用function的pr…...

2023NOIP A层联测9-天竺葵
天竺葵/无法阻挡的子序列/很有味道的题目 我们称一个长度为 k k k 的序列 c c c 是好的,当且仅当对任意正整数 i i i 在 [ 1 , k − 1 ] [1,k-1] [1,k−1] 中,满足 c i 1 > b i c i c_{i1}>b_i \times c_i ci1>bici, …...
react antd table表格点击一行选中数据的方法
一、前言 antd的table,默认是点击左边的单选/复选按钮,才能选中一行数据; 现在想实现点击右边的部分,也可以触发操作选中这行数据。 可以使用onRow实现,样例如下。 二、代码 1.表格样式部分 //表格table样式部分{…...
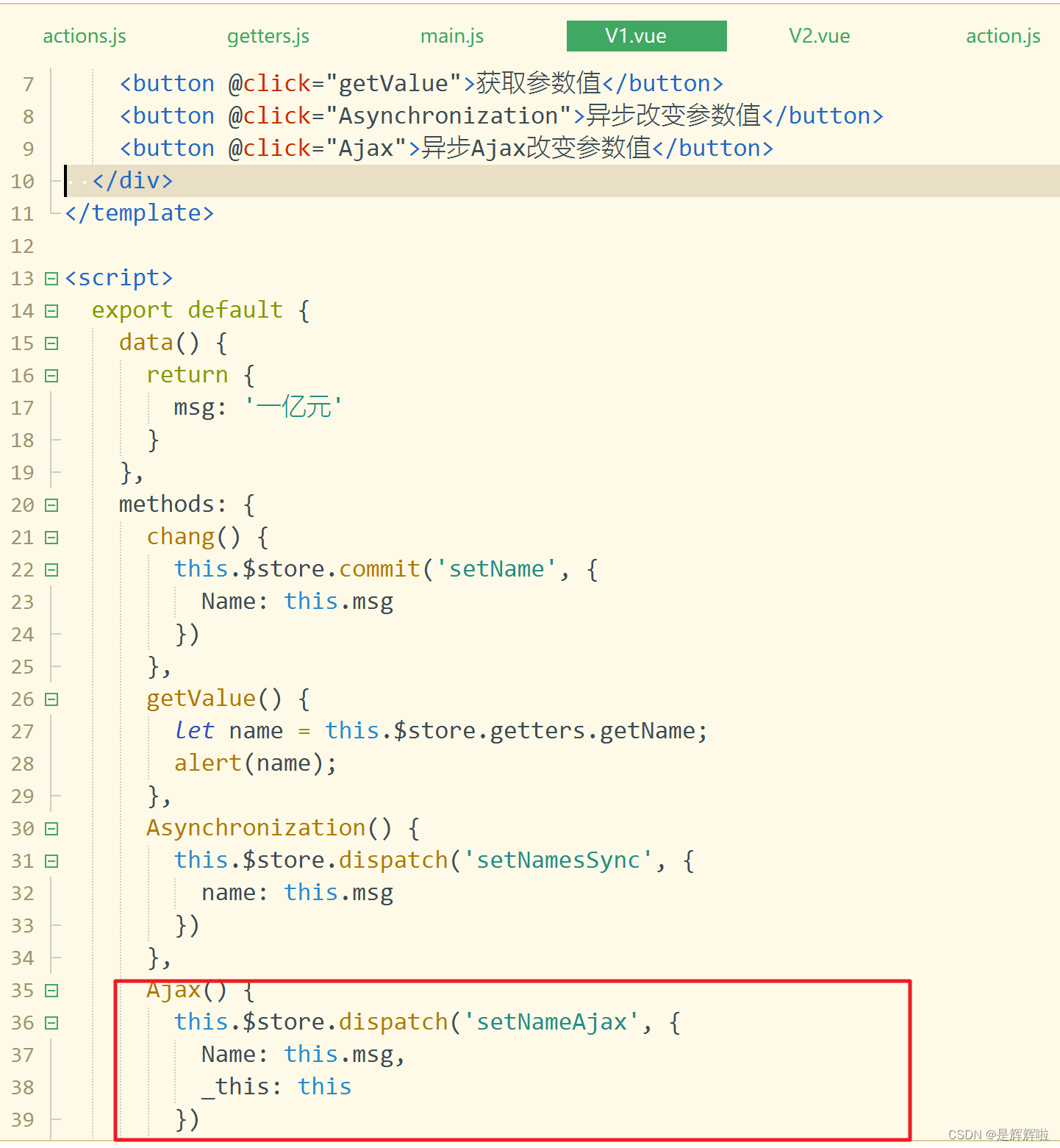
【VUEX】最好用的传参方式--Vuex的详解
🥳🥳Welcome Huihuis Code World ! !🥳🥳 接下来看看由辉辉所写的关于VuexElementUI的相关操作吧 目录 🥳🥳Welcome Huihuis Code World ! !🥳🥳 一.Vuex是什么 1.定义 2…...
)
【.net core】yisha框架 SQL SERVER数据库 反向递归查询部门(子查父)
业务service.cs中ListFilter方法中内容 //反向递归查询部门列表List<DepartmentEntity> departmentList await departmentService.GetReverseRecurrenceList(new DepartmentListParam() { Ids operatorInfo.DepartmentId.ToString() });if (departmentList ! null &am…...
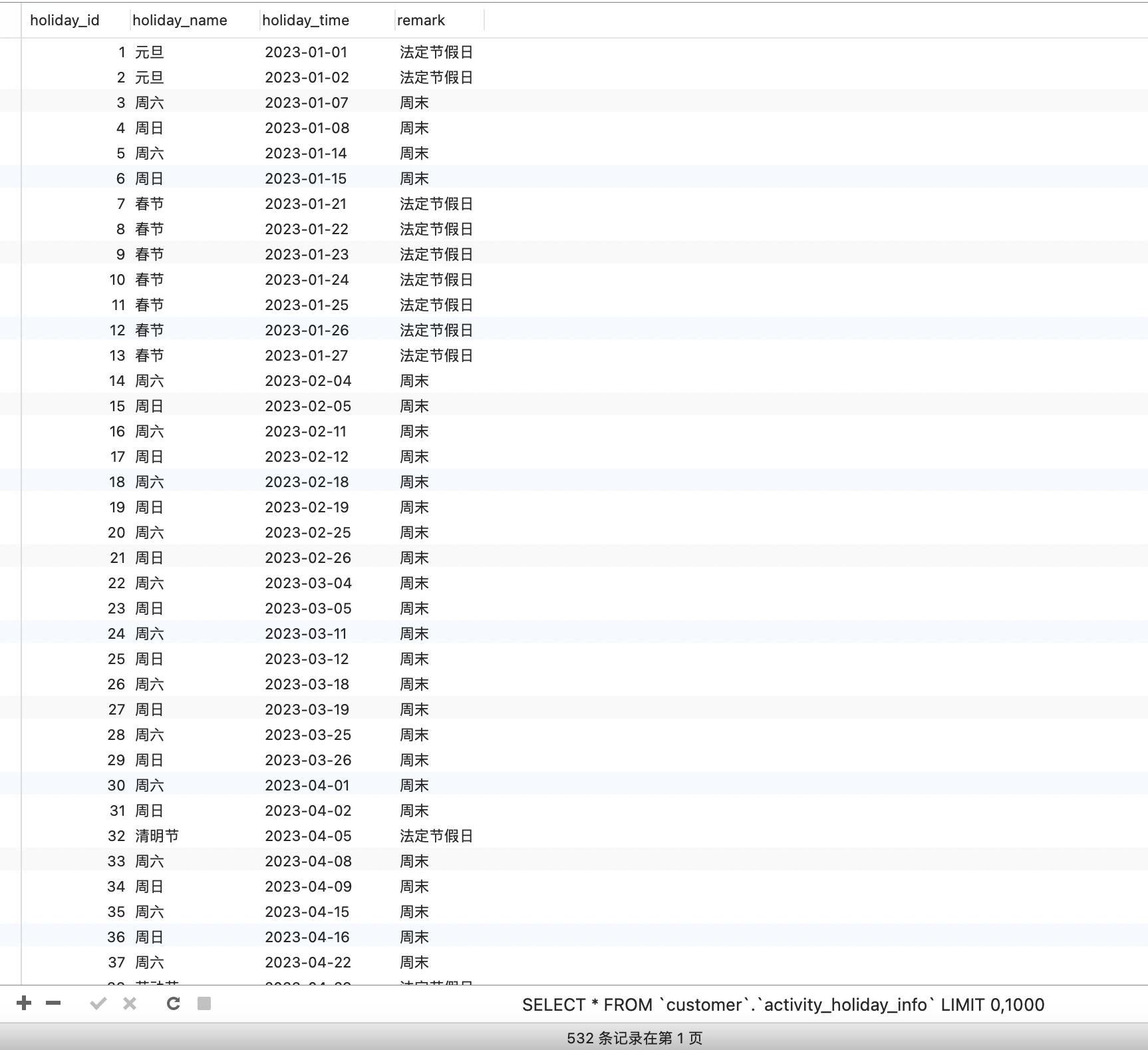
java处理时间-去除节假日以及双休日
文章目录 一、建表:activity_holiday_info二、java代码1、ActivitityHolidayController.java2、ActivityHolidayInfoService.java3、ActivityHolidayInfoServiceImpl.java 三、测试效果 有些场景需要计算数据非工作日的情况,eg:统计每个人每月工作日签到…...

快讯|Tubi 有 Rabbit AI 啦
在每月一期的 Tubi 快讯中,你将全面及时地获取 Tubi 最新发展动态,欢迎星标关注【比图科技】微信公众号,一起成长变强! Tubi 推出 Rabbit AI 帮助用户找到喜欢的视频内容 Tubi 于今年九月底推出了 Rabbit AI,这是一项…...

Zookeeper从入门到精通
Zookeeper 是一个开源的分布式协调服务,目前由 Apache 进行维护。Zookeeper 可以用于实现分布式系统中常见的发布/订阅、负载均衡、命令服务、分布式协调/通知、集群管理、Master 选举、分布式锁和分布式队列等功能。 目录 01-Zookeeper特性与节点数据类型详解02-Z…...
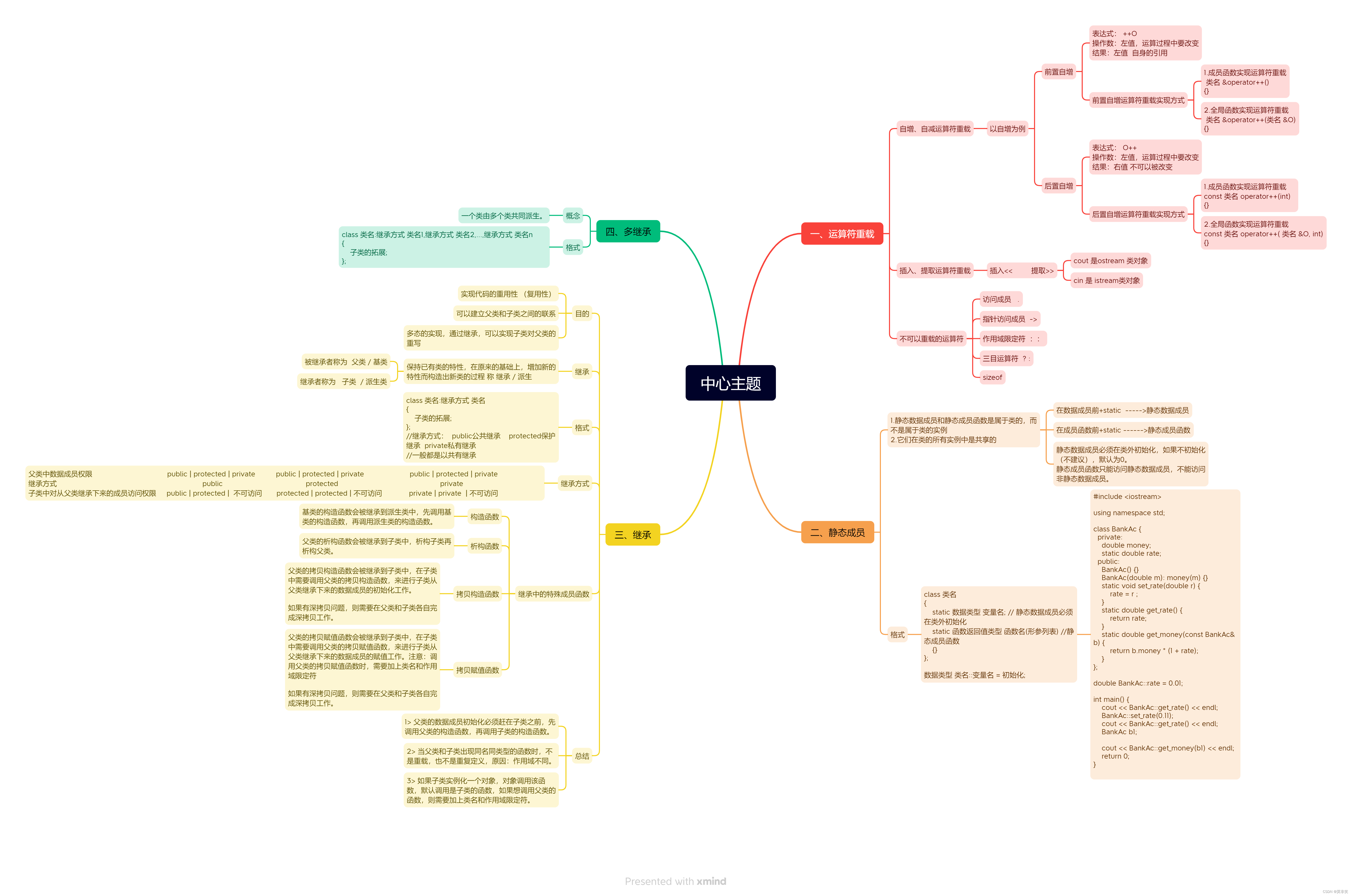
10.11作业
多继承代码实现沙发床 #include <iostream>using namespace std;class Sofa {private:int h;public:Sofa() {cout << "Sofa无参构造" << endl;}Sofa(int h): h(h) {cout << "Sofa有参构造" << endl;}Sofa(const Sofa& …...
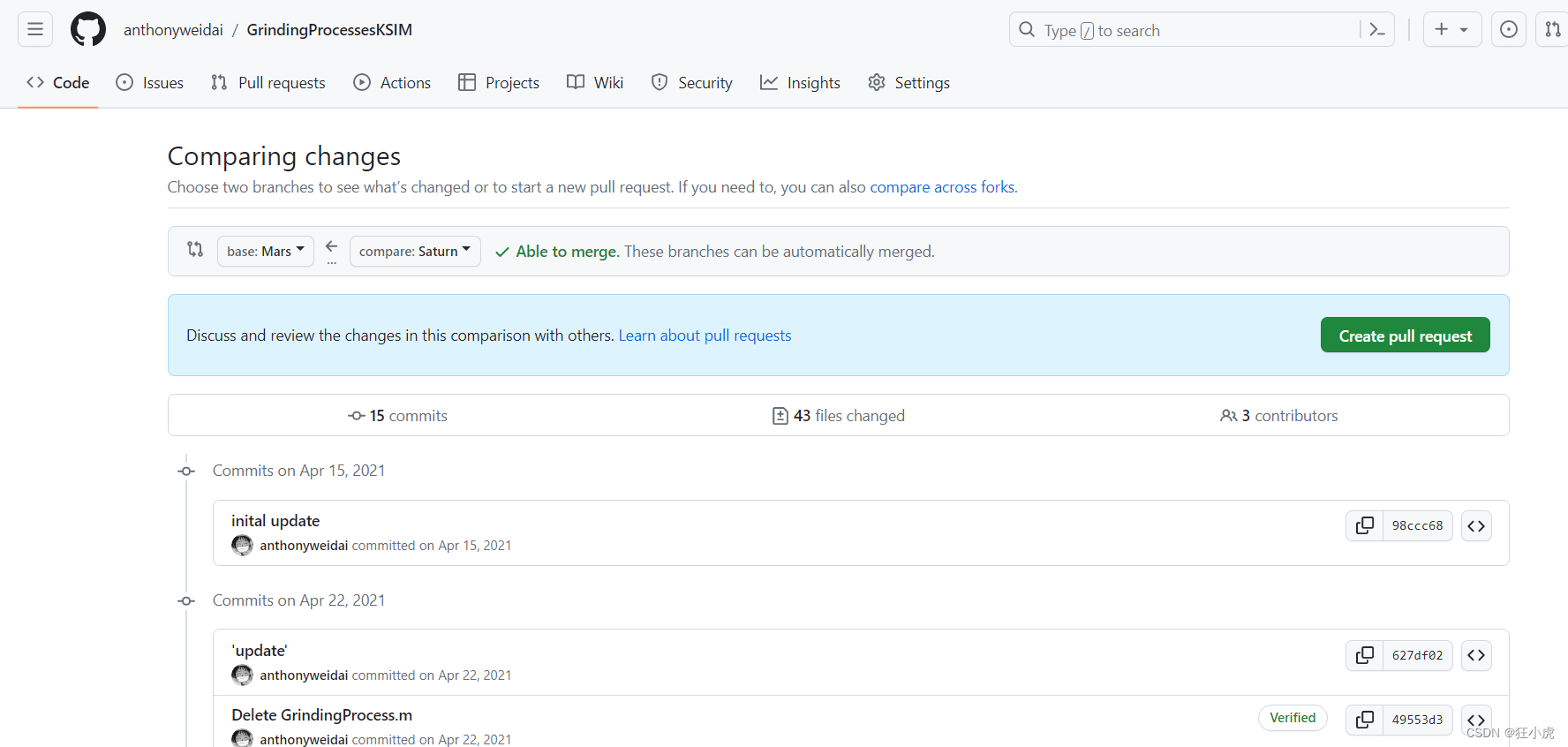
如何对比github中不同commits的区别
有时候想要对比跨度几十个commits之前的代码区别,想直接使用github的用户界面。可以直接在官网操作。 示例 首先要创建一个旧commit的branch。进入该旧的commit,然后输入branch名字即可。 然后在项目网址后面加上compare即可对比旧的branch和新的bran…...

串的基本操作(数据结构)
串的基本操作 #include <stdlib.h> #include <iostream> #include <stdio.h> #define MaxSize 255typedef struct{char ch[MaxSize];int length; }SString;//初始化 SString InitStr(SString &S){S.length0;return S; } //为了方便计算,串的…...

label-studio的使用教程(导入本地路径)
文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...

AGain DB和倍数增益的关系
我在设置一款索尼CMOS芯片时,Again增益0db变化为6DB,画面的变化只有2倍DN的增益,比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析: 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...

Linux 中如何提取压缩文件 ?
Linux 是一种流行的开源操作系统,它提供了许多工具来管理、压缩和解压缩文件。压缩文件有助于节省存储空间,使数据传输更快。本指南将向您展示如何在 Linux 中提取不同类型的压缩文件。 1. Unpacking ZIP Files ZIP 文件是非常常见的,要在 …...

Git常用命令完全指南:从入门到精通
Git常用命令完全指南:从入门到精通 一、基础配置命令 1. 用户信息配置 # 设置全局用户名 git config --global user.name "你的名字"# 设置全局邮箱 git config --global user.email "你的邮箱example.com"# 查看所有配置 git config --list…...
