银行家算法
银行家算法
银行家算法是一种用来避免操作系统死锁出现的有效算法,所以在引入银行家算法的解释之前,有必要简单介绍一下死锁的概念。
一、死锁
死锁:是指两个或两个以上的进程在执行过程中,由于竞争资源或者由于彼此通信而造成的一种阻塞的现象,若无外力的作用,它们都将无法推进下去。此时称系统处于死锁状态或系统产生了死锁,这些永远在互相等待的进程称为死锁进程。
死锁的发生必须具备以下四个必要条件:
1.互斥条件:指进程对所分配到的资源进行排他性使用,即在一段时间内某资源只由一个进程占用。如果此时还有其它进程请求资源,则请求者只能等待,直至占有资源的进程释放。
2.请求和保持条件:指进程已经保持至少一个资源,但又提出了新的资源请求,而该资源已被其它进程占有,此时请求进程阻塞,但又对自己获得的其它资源保持不放。
3.不抢占条件:指进程已获得的资源,在未使用完之前,不能被剥夺,只能在使用完后由自己释放。
4.循环等待条件:指在发生死锁时,必然存在一个进程—资源的环形链。
避免死锁算法中最有代表性的算法就是Dijkstra E.W 于1968年提出的银行家算法,银行家算法是避免死锁的一种重要方法,防止死锁的机构只能确保上述四个条件之一不出现,则系统就不会发生死锁。
二、银行家算法
安全序列: 是指一个进程序列是安全的,即对于每一个进程,它以后尚需要的资源量不超过系统当前剩余资源量与所有进程当前占有的资源量之和。
安全状态: 如果存在一个由系统中所有进程构成的安全序列,则系统处于安全状态。安全状态一定是没有死锁发生。
不安全状态: 不存在一个安全序列。不安全状态不一定导致死锁。
数据结构:
1)可利用资源向量Available
是个含有m个元素的数组,其中的每一个元素代表一类可利用的资源数目。如果Available[j]=K,则表示系统中现有Rj类资源K个。
2)最大需求矩阵Max
这是一个n×m的矩阵,它定义了系统中n个进程中的每一个进程对m类资源的最大需求。如果Max[i,j]=K,则表示进程i需要Rj类资源的最大数目为K。
3)分配矩阵Allocation
这也是一个n×m的矩阵,它定义了系统中每一类资源当前已分配给每一进程的资源数。如果Allocation[i,j]=K,则表示进程i当前已分得Rj类资源的 数目为K。
4)需求矩阵Need
这也是一个n×m的矩阵,用以表示每一个进程尚需的各类资源数。如果Need[i,j]=K,则表示进程i还需要Rj类资源K个,方能完成其任务。
存在的关系:Need[i,j]=Max[i,j]-Allocation[i,j]
Need[i,j]=Max[i,j]-Allocation[i,j]
银行家算法步骤
设Request(i)是进程Pi的请求向量,如果Request(i)[j]=k,表示进程Pi需要K个R(j)类型的资源。当Pi发现资源请求后系统将进行下列步骤
(1)如果Request(i)[j] <= Need[i,j],边转向步骤2),否则认为出错,因为它所请求的资源数已超过它所宣布的最大值。
(2)如果Request(i)[j] <= Available[i,j],便转向步骤3),否则,表示尚无足够资源,Pi需等待。
(3)系统试探着把资源分配给进程Pi,并需要修改下面数据结构中的数值;
Available[j] = Available[j] - Request(i)[j];
Allocation[i,j] = Allocation[i,j] + Request(i)[j];
Need[i,j] = Need[i,j] - Request(i)[j];
说了这么多基本的概念,下面就让我们通过实际案例来体会银行算法吧。
三、实战

从图中数据我们可以利用银行家算法的四个数据结构,来描述当前的系统状态
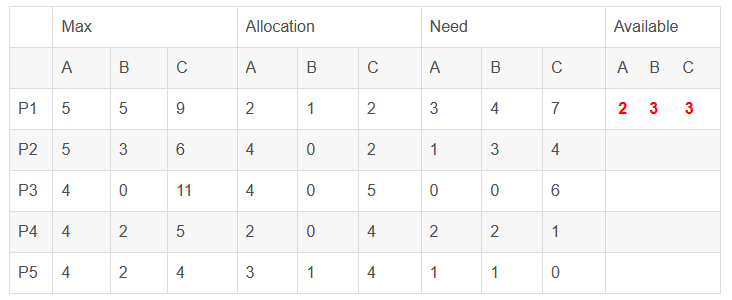
因为系统资源R =(17,5,20)而系统分配给这几个线程的资源为Allocation=(15,2,17) 则可以求出Available=(2,3,3)
(1)在T0时刻,由于Available大于等于Need中 P5 所在行的向量,因此Availabel能满足 P5 的运行,在 P5 运行后,系统的状态变更为如下图所示:
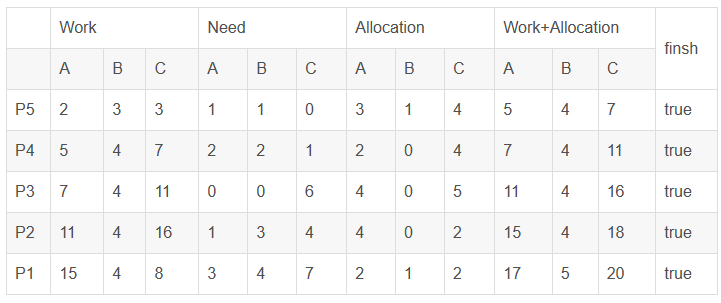
因此,在T0时刻,存在安全序列:P5,P4,P3,P2,P1(并不唯一)
(2)P2请求资源,P2发出请求向量Request(i)(0,3,4),系统根据银行家算法进行检查;
① P2 申请资源Reuqest(i)(0,3,4)<=Need中 P2 所在行向量Need(i)(1,3,4)
② P2 申请资源Reuqest(i)(0,3,4)>=可以利用资源向量Availabel(2,3,3),所以,该申请不给于分配
(3)P4请求资源,P4发出请求向量Request(i)(2,0,1),系统根据银行家算法进行检查;
①Reuqest(i)(2,0,1)<= Need(i)(2,2,1)
② Reuqest(i)(2,0,1 <= Availabel(2,3,3)
③对 P4 的申请(2,0,1)进行预分配后,系统的状态为:

可利用资源向量Availabel=(0,3,2),大于Need中 P4 所在行的向量(0,2,0),因此可以满足 P4 的运行。P4 运行结束后,系统的状态变为:
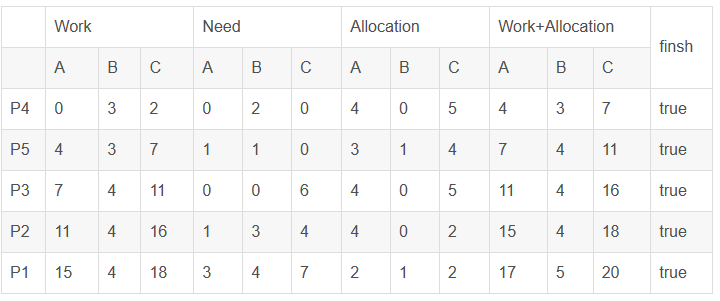
同理依次推导,可计算出存在安全序列P4,P5,P3,P2,P1(并不唯一)
(4)P1请求资源,P1发出请求向量Request(i)(0,2,0),系统根据银行家算法进行检查;
①Request(i)(0,2,0)<= Need(i)(3,4,7)
② Request(i)(0,2,0)<= Availabel(2,3,3)
③对 P1 的申请(0,2,0)进行预分配后,系统的状态为:
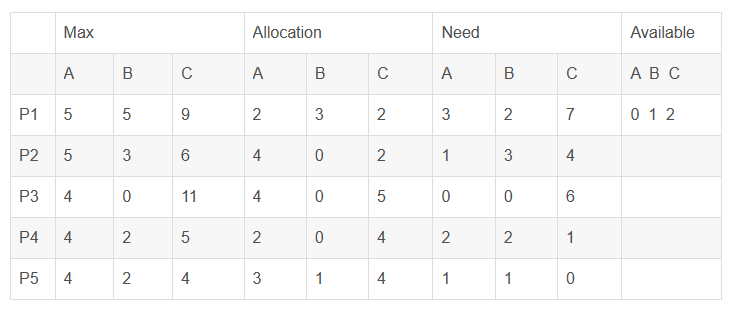
由于Available不大于等于 P1 到 P5 任一进程在Need中的需求向量,因此系统进行预分配后
处于不安全状态,所以对于 P1 申请资源(0,2,0)不给予分配。
注意:因为(4)是建立在第(3)问的基础上的所以Available=(0,3,2)-(0,2,0)=(0,1,2)
向量,因此系统进行预分配后
处于不安全状态,所以对于 P1 申请资源(0,2,0)不给予分配。
注意:因为(4)是建立在第(3)问的基础上的所以Available=(0,3,2)-(0,2,0)=(0,1,2)
相关文章:

银行家算法
银行家算法 银行家算法是一种用来避免操作系统死锁出现的有效算法,所以在引入银行家算法的解释之前,有必要简单介绍一下死锁的概念。 一、死锁 死锁:是指两个或两个以上的进程在执行过程中,由于竞争资源或者由于彼此通信而造成…...
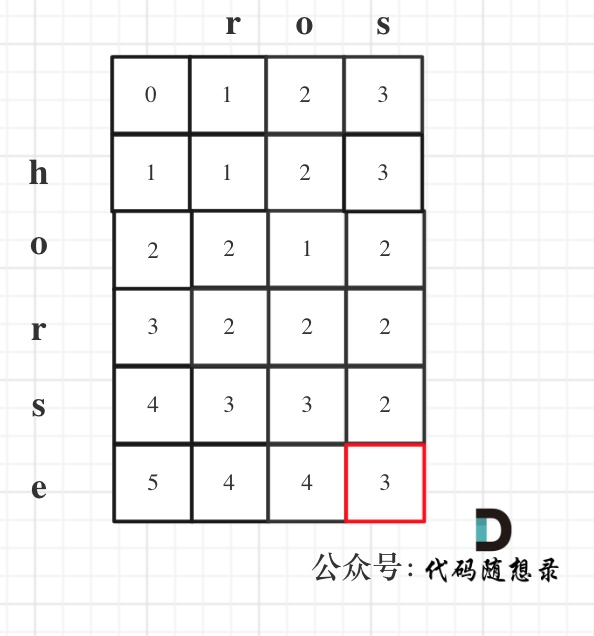
181、【动态规划】leetcode ——72. 编辑距离(C++版本)
题目描述 原题链接:72. 编辑距离 解题思路 动态规划五步曲: (1)dp[i][j]含义: 以word1[i - 1]和word2[j - 1]结尾子串,经过最少次增删改后,可让word1变为word2的步数。dp中的i对应word1中的i…...

mysql 中关于慢查询日志
慢查询日志 慢查询日志主要用来记录执行时间超过设置的某个时长的SQL语句,能够帮助数据库维护人员找出执行时间比较长、执行效率比较低的SQL语句,并对这些SQL语句进行针对性优化。 开启慢查询 可以在 my.cnf 文件或者 my.ini 文件中配置开启慢查询日志…...

程序员必备的软技能-金字塔原理拆解(上)
原书 290千字,本文预计 14千字,拆解比 20:1,预计阅读时长 15分钟序言日常工作中,常常因为思维、表达方式不对产生不想要的结果:写了一个小时的周报,领导却不满意?跟团队讲了半天自己…...

关于我利用python开发的PC端标注软件及目标检测软件
如何利用python快速开发PC端目标检测及数据标注软件概述开发软件背景开发第一步:功能需求分析开发第二步: 前端分区设计开发第三步:功能开发开发第四步:程序功能的打包与检查开发第五步:程序的反馈与改善一个例子的展示…...
Git导出增量包的操作步骤
前言在项目开发部署中,通常是将一个Git项目全量打包发布,但有的场景只需要导出有变更的那部分文件,增量发布,此时就需要使用Git导出增量包了。一、查看提交记录拿到提交ID码①例如使用的gitlab使用方法参考下图(一目了然) 【推荐】…...
JavaWeb--JavaScript
JavaScript1 JavaScript简介2 JavaScript引入方式2.1 内部脚本2.2 外部脚本3 JavaScript基础语法3.1 书写语法3.2 输出语句3.3 变量3.4 数据类型3.5 运算符3.5.1 \\ 和 区别3.5.2 类型转换3.6 流程控制语句3.6.1 if 语句3.6.2 switch 语句3.6.3 for 循环语句3.6.4 while 循环语…...
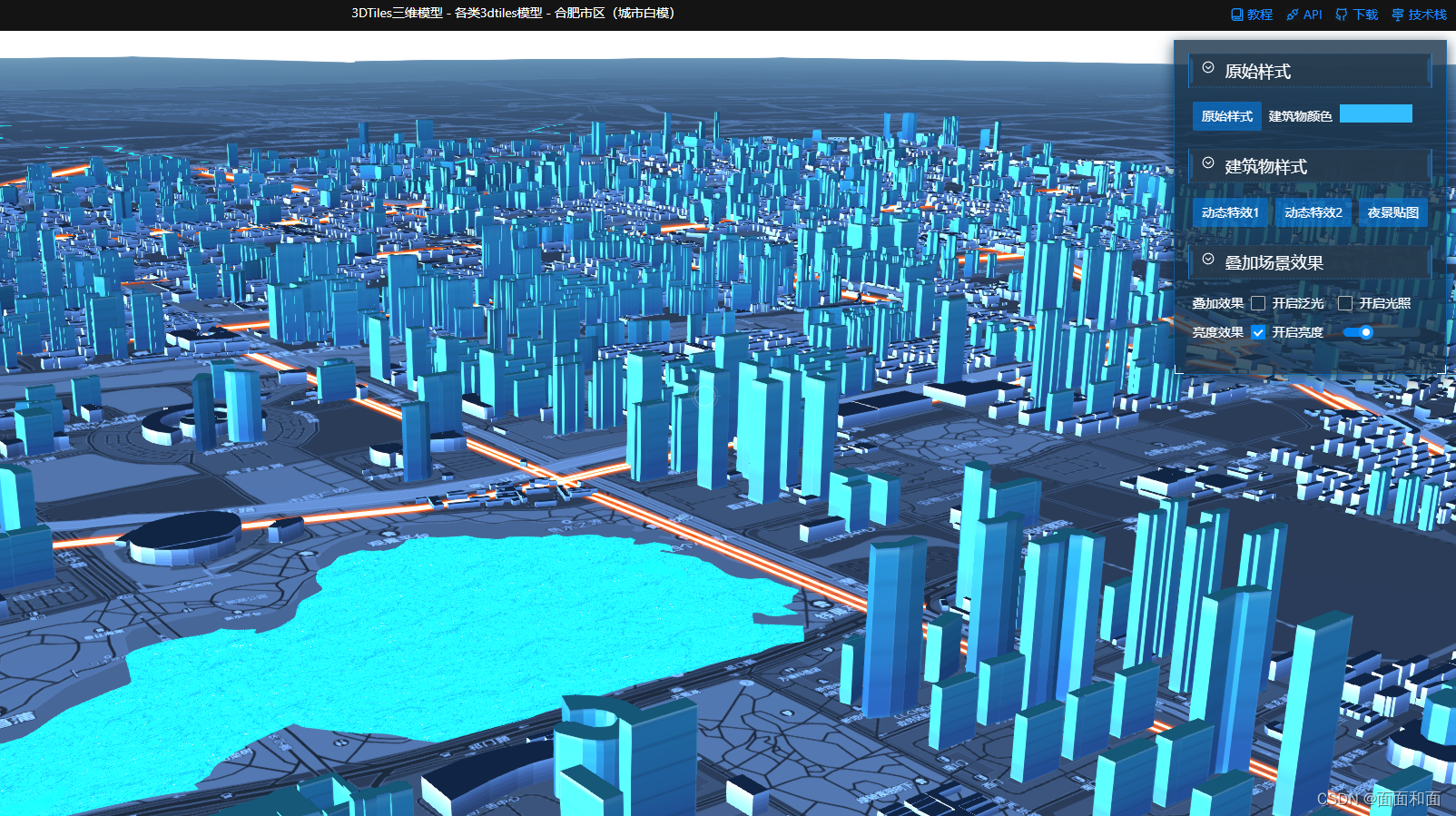
mars3d加载建筑物白膜及简单建筑物样式
首先需要拥有shp格式的数据。可以通过水经微图下载,注意此软件是付费的将shp格式的数据处理为切片数据,可以使用cesiumlab处理完成得到json数据就可以在mars3d中加载了 function init() { // 判断webgl支持 if (!mars3d.Util.webglreport()) { …...
数据结构之顺序表
本章重点: 1.线性表 2.顺序表 3.链表 4.顺序表和链表的区别和联系 目录 1.线性表 2.顺序表 2.1概念及结构 2.2接口实现 2.2.1 SeqList.h 2.2.2 SeqList.c 2.3数组相关面试题 2.3.1移除元素 2.3.2删除有序数组中的重复项 编辑 2.3.3合并两个有序数组…...

【数据挖掘实战】——家用电器用户行为分析及事件识别
项目地址:Datamining_project: 数据挖掘实战项目代码 目录 一、背景和挖掘目标 1、问题背景 2、原始数据 3、挖掘目标 二、分析方法与过程 1、初步分析 2、总体流程 第一步:数据抽取 第二步:探索分析 第三步:数据的预处…...

肠道核心菌属——双歧杆菌属,了解并拥有它
双歧杆菌 双歧杆菌属(Bifidobacterium)是放线菌门严格厌氧的革兰氏阳性多形性杆状细菌。末端常常分叉,故名双歧杆菌。是人和动物肠道的重要核心菌群和有益生理菌群,也是母乳喂养婴儿中发现的第二大菌。 肥胖、糖尿病和过敏等各种疾…...
 和时间序列 - 重采样 resample)
Python 之 Pandas 生成时间戳范围、Pandas 的时期函数 Period() 和时间序列 - 重采样 resample
文章目录一、生成时间戳范围1. 指定值2. 指定开始日期并设置期间数3. 频率 freq4. closed二、Pandas 的时期函数 Period()三、时间序列 - 重采样 resample在开始之前,我们先导入 numpy 和 pandas 库,同时导入 python 内置的模块。 import pandas as pd…...
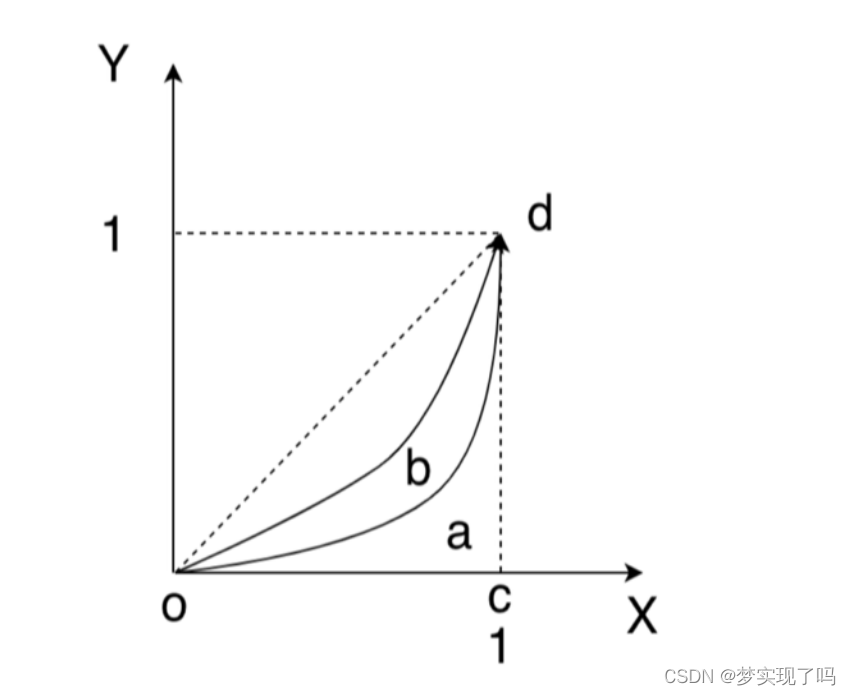
利用Python和Sprak求曲线与X轴上方的面积
有n组标本(1, 2, 3, 4), 每组由m个( , , ...)元素( , )组成(m值不定), . 各组样本的分布 曲线如下图所示. 通过程序近似实现各曲线与oc, cd直线围成的⾯积. 思路 可以将图像分成若干个梯形,每个梯形的底边长为(Xn1 - Xn-1),面积为矩形的一半,…...

利用机器学习(mediapipe),进行人手的21个3D手关节坐标检测
感知手的形状和动作的能力可能是在各种技术领域和平台上改善用户体验的重要组成部分。例如,它可以构成手语理解和手势控制的基础,并且还可以在增强现实中将数字内容和信息覆盖在物理世界之上。虽然自然而然地出现在人们手中,但是强大的实时手感知力无疑是一项具有挑战性的计…...
【添砖java】谁说编程第一步是hello world
编程第一步明明是下载编译器和配置环境(小声逼逼)。 Windows下的java环境安装: java的安装包分为两类,一类是JRE(Java Runtime Environmental),是一个独立的java运行环境;一类是JDK…...
el-table大数据量渲染卡顿问题
1、场景描述 在项目开发中,遇到在表格中一次性加载完的需求,且加载数量不少,有几百几千条,并且每条都可能有自己的下拉框,输入框来做编辑功能,此时普通的el-table肯定会导致浏览器卡死,那么怎么…...

MyBatis-Plus 实现分页的几种写法
简介MyBatis-Plus (opens new window)(简称 MP)是一个 MyBatis (opens new window)的增强工具,在 MyBatis 的基础上只做增强不做改变,为简化开发、提高效率而生。快速开始添加依赖全新的 MyBatis-Plus 3.0 版本基于 JDK8ÿ…...

记一次Binder内存不足导致的应用被杀
每个进程的可用Binder内存大小是 1M-8KB 也就是900多KB 事情的起因的QA压测过程发生进程号变更,怀疑APP被杀掉过,于是开始看日志(实际后来模拟的时候可以发现app确实被杀掉了) APP的压测平台会上报进程号变更时间点,发…...

Zabbix4.0架构理解-zabbix的工作方式
目录 1.1、zabbix4.0架构图 1.2、zabbix的进程 1、 zabbix server 2、zabbix agent 3、 zabbix proxy 4、 java gateway 5、zabbix get 1.3、zabbix的几种工作方式 1、通过zabbix agent 2、通过zabbix proxy 3、通过 zabbix java gateway 4、其他 1.3、zabbix 数据走…...
MySQL中的一些非常实用的函数、语法
前言我最近几年用MYSQL数据库挺多的,发现了一些非常有用的小玩意,今天拿出来分享到大家,希望对你会有所帮助。1.group_concat在我们平常的工作中,使用group by进行分组的场景,是非常多的。比如想统计出用户表中&#x…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

Cesium1.95中高性能加载1500个点
一、基本方式: 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...

算法岗面试经验分享-大模型篇
文章目录 A 基础语言模型A.1 TransformerA.2 Bert B 大语言模型结构B.1 GPTB.2 LLamaB.3 ChatGLMB.4 Qwen C 大语言模型微调C.1 Fine-tuningC.2 Adapter-tuningC.3 Prefix-tuningC.4 P-tuningC.5 LoRA A 基础语言模型 A.1 Transformer (1)资源 论文&a…...

深度学习水论文:mamba+图像增强
🧀当前视觉领域对高效长序列建模需求激增,对Mamba图像增强这方向的研究自然也逐渐火热。原因在于其高效长程建模,以及动态计算优势,在图像质量提升和细节恢复方面有难以替代的作用。 🧀因此短时间内,就有不…...

Xela矩阵三轴触觉传感器的工作原理解析与应用场景
Xela矩阵三轴触觉传感器通过先进技术模拟人类触觉感知,帮助设备实现精确的力测量与位移监测。其核心功能基于磁性三维力测量与空间位移测量,能够捕捉多维触觉信息。该传感器的设计不仅提升了触觉感知的精度,还为机器人、医疗设备和制造业的智…...

[USACO23FEB] Bakery S
题目描述 Bessie 开了一家面包店! 在她的面包店里,Bessie 有一个烤箱,可以在 t C t_C tC 的时间内生产一块饼干或在 t M t_M tM 单位时间内生产一块松糕。 ( 1 ≤ t C , t M ≤ 10 9 ) (1 \le t_C,t_M \le 10^9) (1≤tC,tM≤109)。由于空间…...

Python的__call__ 方法
在 Python 中,__call__ 是一个特殊的魔术方法(magic method),它允许一个类的实例像函数一样被调用。当你在一个对象后面加上 () 并执行时(例如 obj()),Python 会自动调用该对象的 __call__ 方法…...

安全领域新突破:可视化让隐患无处遁形
在安全领域,隐患就像暗处的 “幽灵”,随时可能引发严重事故。传统安全排查手段,常常难以将它们一网打尽。你是否好奇,究竟是什么神奇力量,能让这些潜藏的隐患无所遁形?没错,就是可视化技术。它如…...
