代码随想录Day14 LeetCodeT110平衡二叉树 T257二叉树的所有路径 T404 左叶子之和
以下思路来自于: 代码随想录 (programmercarl.com)
LeetCode T110 平衡二叉树
题目链接:110. 平衡二叉树 - 力扣(LeetCode)
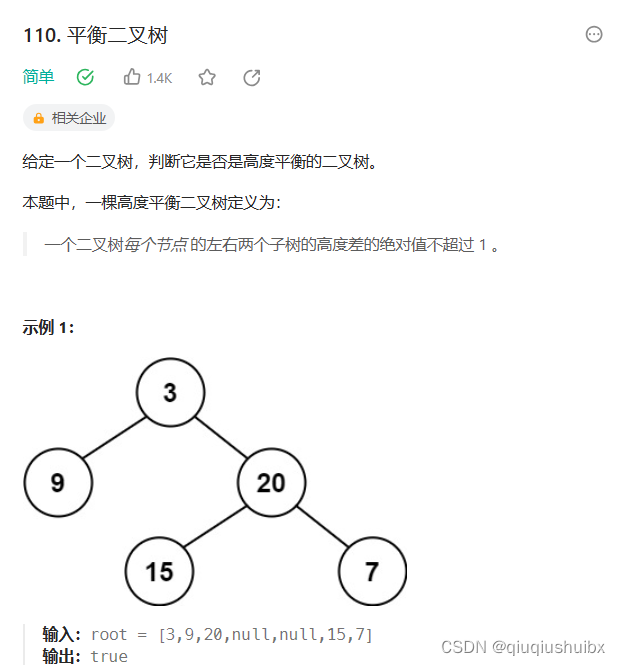
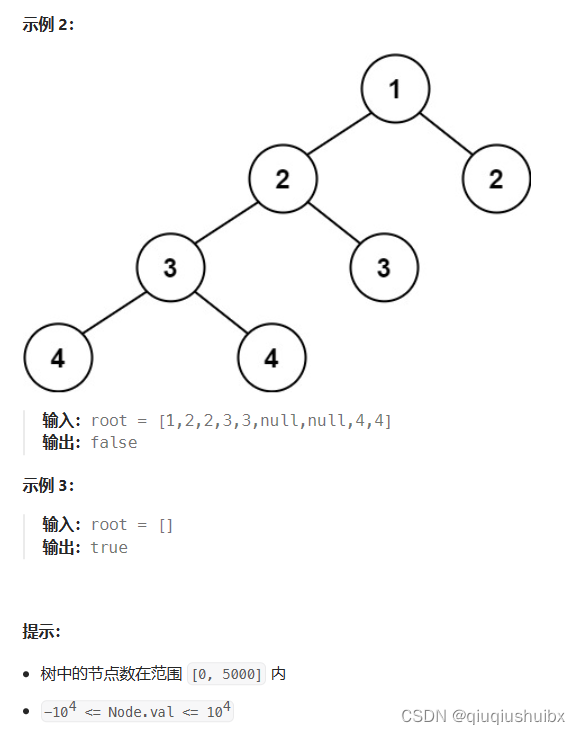
题目思路
前面我们说过了,求二叉树的深度我们应该使用前序遍历,求二叉树的高度我们应该使用后序遍历,因为后序遍历可以将子树的高度返回给父节点,这样层层递归就能得到答案,而深度是从根节点下去一直到空节点为止,这里清楚了这个逻辑,我们就可以来做这道题了,我们知道一个平衡二叉树的高度差是小于等于1的,而不是平衡二叉树的话只需任意子树的高度大于即可,这里我们仍然使用递归完成
1.确定参数和返回值
求高度,返回值是int 只需传入一个节点即可
int getHeight(TreeNode node)2.确定终止条件
这里我们遇到空节点处即可返回
if(node == null){return 0;}3.确定一次递归逻辑
我们默认如果不是平衡二叉树就返回-1即可,我们按照左右根进行遍历
注:每次获取完左右子树记得判断一次
int leftHeight = getHeight(node.left);if(leftHeight == -1){return -1;}int rightHeight = getHeight(node.right);if(rightHeight == -1){return -1;}if(Math.abs(rightHeight-leftHeight)>1){return -1;}else{return 1+Math.max(leftHeight,rightHeight);}
题目代码
class Solution {public boolean isBalanced(TreeNode root) {return getHeight(root) != -1;}int getHeight(TreeNode node){if(node == null){return 0;}int leftHeight = getHeight(node.left);if(leftHeight == -1){return -1;}int rightHeight = getHeight(node.right);if(rightHeight == -1){return -1;}if(Math.abs(rightHeight-leftHeight)>1){return -1;}else{return 1+Math.max(leftHeight,rightHeight);}}
}LeetCode T257 二叉树的所有路径
题目链接:257. 二叉树的所有路径 - 力扣(LeetCode)
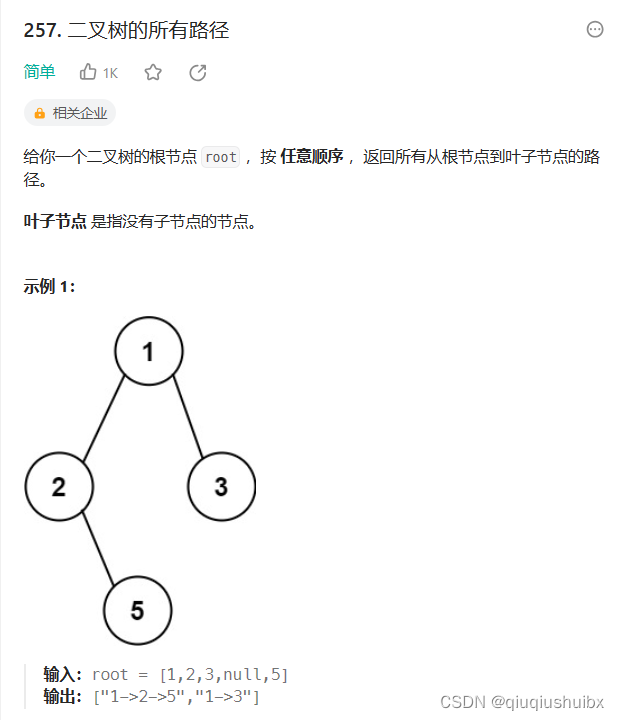

题目思路
这里我们注意,使用到了回溯算法,其实递归和回溯是相辅相成的,就以上题的示例1为例,我们再记录了125这一条路线的时候还得回去记录13这一条路径,这就用到了回溯.这里千万不要把递归和回溯拆开,因为有一个递归就有一个回溯.
题目代码
class Solution {public List<String> binaryTreePaths(TreeNode root) {List<String> res = new ArrayList<>();if(root == null){return null;}List<Integer> path = new ArrayList<>();travsal(root,path,res);return res;}void travsal(TreeNode node,List<Integer> path,List<String> res){//前序path.add(node.val);if(node.left == null && node.right == null){StringBuilder sb = new StringBuilder();for(int i = 0;i<path.size()-1;i++){sb.append(path.get(i)).append("->");}sb.append(path.get(path.size()-1));res.add(sb.toString());}if(node.left != null){//一次递归一次回溯travsal(node.left,path,res);path.remove(path.size()-1);}if(node.right != null){travsal(node.right,path,res);path.remove(path.size()-1);}}
}LeetCode T404 左叶子之和
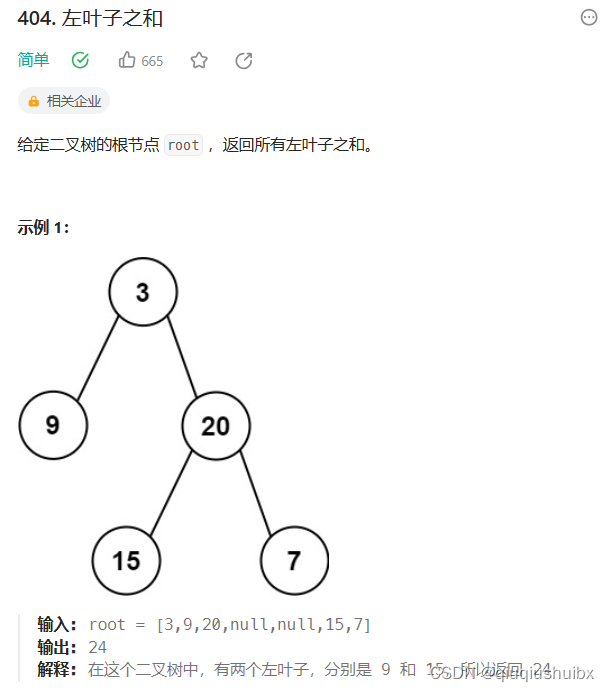

题目链接:力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台
题目思路
这里我们注意之前我们只能判断叶子结点,而不能知道左叶子节点,这里我们就可以用过叶子结点的上一个节点知道是否为左叶子节点,这里我们仍然使用递归实现,这里就不需要额外创建新函数(仍然使用后序遍历)
1.函数返回值和参数
public int sumOfLeftLeaves(TreeNode root)
2.终止条件无论是遇到空节点或者叶子节点都返回0,因为我们不知道该叶子结点是否为我们需要收集的节点
if(root == null){return 0;}if(root.left == null && root.right == null){return 0;}3.单层递归
//后序int leftNum = sumOfLeftLeaves(root.left);int rightNum = sumOfLeftLeaves(root.right);int sum = 0;//中间处理过程if(root.left != null && root.left.left == null && root.left.right == null){sum = root.left.val;}sum = sum + leftNum + rightNum;return sum;
题目代码
class Solution {public int sumOfLeftLeaves(TreeNode root) {if(root == null){return 0;}if(root.left == null && root.right == null){return 0;}//后序int leftNum = sumOfLeftLeaves(root.left);int rightNum = sumOfLeftLeaves(root.right);int sum = 0;if(root.left != null && root.left.left == null && root.left.right == null){sum = root.left.val;}sum = sum+leftNum+rightNum;return sum;}}相关文章:

代码随想录Day14 LeetCodeT110平衡二叉树 T257二叉树的所有路径 T404 左叶子之和
以下思路来自于: 代码随想录 (programmercarl.com) LeetCode T110 平衡二叉树 题目链接:110. 平衡二叉树 - 力扣(LeetCode) 题目思路 前面我们说过了,求二叉树的深度我们应该使用前序遍历,求二叉树的高度我们应该使用后序遍历,因为后序遍历可以将子树的…...
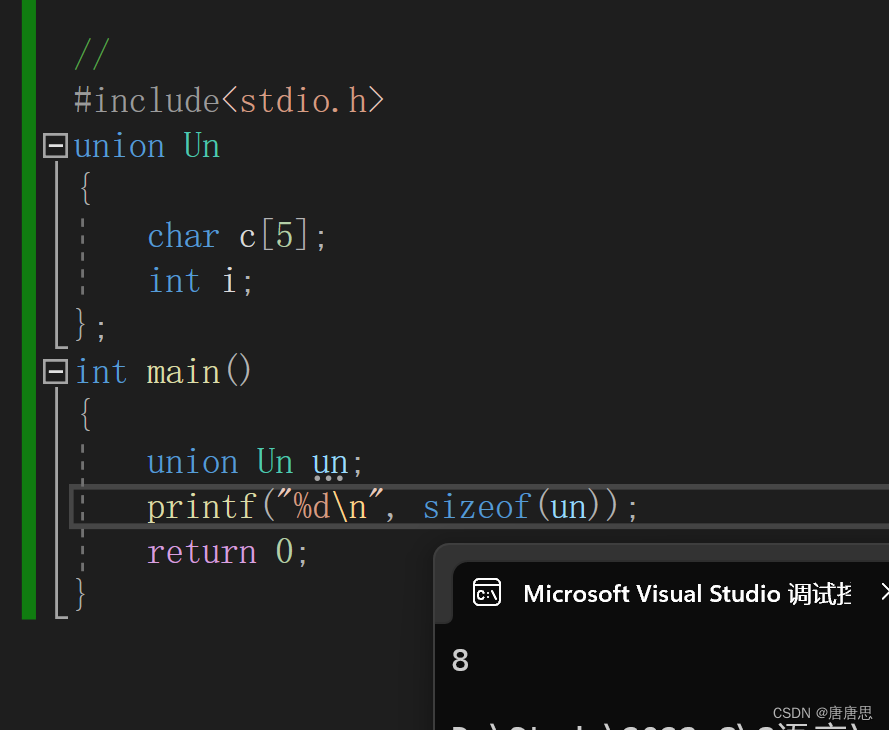
C语言自定义类型_枚举联合(3)
目录 枚举 什么是枚举类型? 枚举的声明 枚举的定义 枚举的优点 枚举的使用 联合(共用体) 什么是联合呢? 联合类型的定义 联合的特点 联合使用 联合大小的计算 联合的应用 今天接着我们来结束自定义类型。Ἑ…...
asp.net网上销售系统VS开发mysql数据库web结构c#编程Microsoft Visual Studio计算机毕业设计
一、源码特点 asp.net 网上销售系统 是一套完善的web设计管理系统,系统具有完整的源代码和数据库,系统主要采用B/S模式开发。开发环境为vs2010,数据库为mysql,使用c#语言开发 aspnet 网上销售系统1 二、功能介绍 前台功能…...
【Windows】RPC调用过程实例详解
概述:windows 创建 RPC调用过程实例详解 参考文章:Remote procedure call (RPC)(远程过程调用 (RPC)) - Win32 apps | Microsoft Learn 文章目录 0x01、生成 UUID 和模版(IDL)文件0x02、添加 acf 文件0x03、编译 idl 文件0x04、客…...
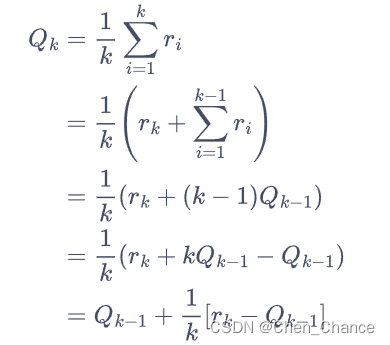
动手学强化学习第2章多臂老虎机
2.1简介 多臂老虎机问题可以被看作简化版的强化学习问题。但是其只有动作和奖励没有状态信息,算是简化版的强化学习问题。 2.2问题介绍 2.2.1问题定义 在多臂老虎机(MAB)问题中,有一个有K根拉杆的老虎机,拉动每一根拉杆都对应一个关于奖励…...

钡铼BL124EC实现EtherCAT转Ethernet/IP的优势
钡铼技术的BL124EC是一款用于将EtherCAT从站转换为Ethernet/IP从站的网关设备。它是钡铼技术开发的高性能、可靠的工业自动化通信解决方案之一。 添加图片注释,不超过 140 字(可选) BL124EC网关可以应用于多种工业自动化场景,以下…...

使用IntelliJ Idea必备的插件!
趁手的工具让开发事半功倍,好用的IDEA插件让效率加倍。 今天给大家分享几个优秀的IDEA插件。 插件安装 首先得知道在IDEA哪安装插件? 点击File---->Settings---->找到Plugins标签,即可搜索想要的插件进行安装了。 现在来看下有哪些值…...

代码随想录算法训练营第23期day19| 654.最大二叉树、617.合并二叉树、700.二叉搜索树中的搜索、98.验证二叉搜索树
目录 一、(leetcode 654)最大二叉树 二、(leetcode 617)合并二叉树 三、(leetcode 700)二叉搜索树中的搜索 四、(leetcode 98)验证二叉搜索树 一、(leetcode 654&…...
 459. 重复的子字符串)
第四章 字符串part02 28. 实现strStr() 459. 重复的子字符串
第四章 字符串part02 28. 实现strStr() 459. 重复的子字符串 一、28. 实现strStr() 题目链接:https://leetcode.cn/problems/repeated-substring-pattern/ 题目介绍: 给定一个非空的字符串 s ,检查是否可以通过由它的一个子串重复多次构成。…...
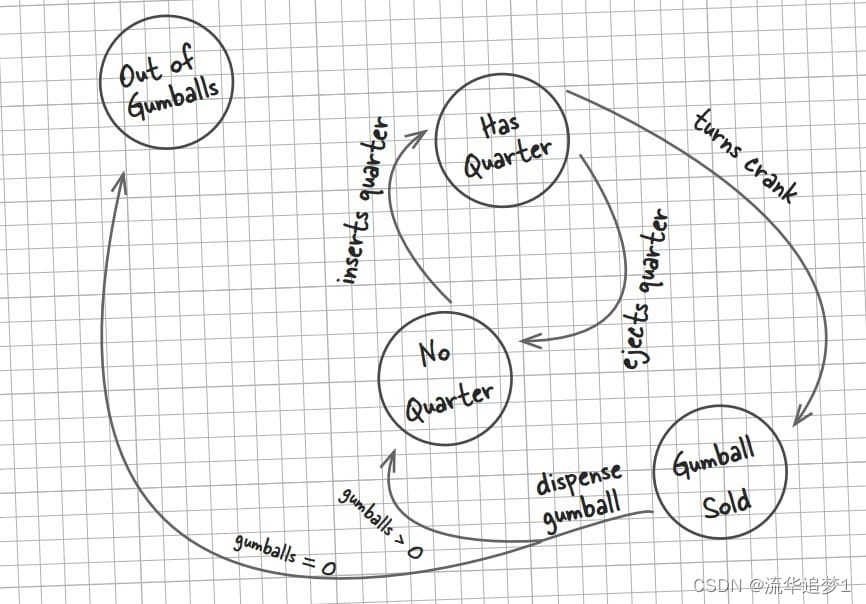
设计模式 - 状态模式
目录 一. 前言 二. 实现 一. 前言 状态模式(State Pattern):它主要用来解决对象在多种状态转换时,需要对外输出不同的行为的问题。状态和行为是一一对应的,状态之间可以相互转换。当一个对象的内在状态改变时&#x…...

【vim 学习系列文章 9 -- .vim 脚本文件开发学习】
文章目录 .vimrc 介绍.vim 脚本文件开发 .vimrc 介绍 在Vim中,你可以将一系列的Vim命令和设置写入一个脚本文件中,并使用:source命令来运行它。这种脚本文件通常被称为vimrc文件,因为它的默认名称是.vimrc。通常,我们将这个文件放…...

NAT模式和桥接模式的区别
NAT模式和桥接模式的区别 NAT模式和桥接模式都是虚拟机网络配置的两种方式,主要区别在于虚拟机与外部网络交互的方式不同。 NAT(Network Address Translation,网络地址转换)模式:在这种模式下,虚拟机和宿主…...

应对出海安全合规挑战,兆珑科技为什么选择了亚马逊云科技?
在中国企业出海进程中,安全合规是企业面临的首要挑战。尤其是当企业业务涉及金融相关领域时,面临着最为严苛的安全合规要求。 深圳兆珑科技有限公司是一家全球化的物联网生态企业,其业务覆盖100多个国家和地区,在欧洲、南美、亚太…...
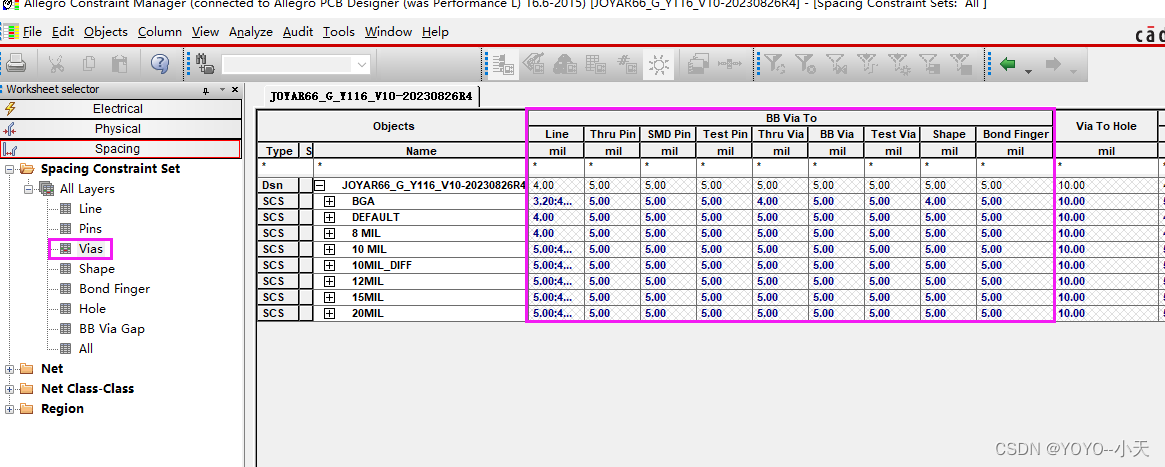
Allegro基本规则设置指导书之Spacing规则设置
进入规则设置界面 1.设置Line 到其他的之间规则: 2.设置Pins 到其他的之间规则: 3.设置Vias 到其他的之间规则:...
使用【Blob、Base64】两种方式显示【文本、图片、视频】 使用 video 组件播放视频
Blob 显示 Blob 对象的类型是由 MIME 类型(Multipurpose Internet Mail Extensions)来确定的。MIME 类型是一种标准,用于表示文档、图像、音频、视频等多媒体文件的类型。以下是一些常见的 Blob 对象类型: text/plain࿱…...

深度学习_1_基本语法
数据结构 代码: import torchx torch.arange(12)##产生长度为12的一维张量print(x)##X x.resize(3, 4)##被弃用##print(X)y torch.reshape(x, (3, 4))##修改向量为矩阵,一维变二维print(y)print(y.size())xx torch.zeros((2, 3, 4))##三维矩阵&…...
c#设计模式-行为型模式 之 中介者模式
🚀简介 又叫调停模式,定义一个中介角色来封装一系列对象之间的交互,使原有对象之间的耦合松散,且可以独立地改变它们之间的交互。 从下右图中可以看到,任何一个类的变 动,只会影响的类本身,以及…...
小程序uView2.X框架upload组件上传方法总结+避坑
呈现效果: 1.1单图片上传 1.2多图片上传 前言:相信很多人写小程序会用到uView框架,总体感觉还算OK吧,只能这么说,肯定也会遇到图片视频上传,如果用到这个upload组件相信你,肯定遇到各种各样的问题,这是我个人总结的单图片和多图片上传方法. uView2.X框架:uView 2.0 - 全面兼容…...

人脸检测及追踪回顾
轻量级人脸检测 代码地址 人脸追踪 代码地址 MNN框架部署文档 文档地址...

虚拟环境和包
目录 12. 虚拟环境和包 12.1. 简介 12.2. 创建虚拟环境 12.3. 使用 pip 管理包 12. 虚拟环境和包 12.1. 简介 Python 应用程序经常会使用一些不属于标准库的包和模块。应用程序有时候需要某个特定版本的库,因为它需要一个特定的 bug 已得到修复的库或者它是使用…...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

LLM基础1_语言模型如何处理文本
基于GitHub项目:https://github.com/datawhalechina/llms-from-scratch-cn 工具介绍 tiktoken:OpenAI开发的专业"分词器" torch:Facebook开发的强力计算引擎,相当于超级计算器 理解词嵌入:给词语画"…...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...

【Java学习笔记】BigInteger 和 BigDecimal 类
BigInteger 和 BigDecimal 类 二者共有的常见方法 方法功能add加subtract减multiply乘divide除 注意点:传参类型必须是类对象 一、BigInteger 1. 作用:适合保存比较大的整型数 2. 使用说明 创建BigInteger对象 传入字符串 3. 代码示例 import j…...

【生成模型】视频生成论文调研
工作清单 上游应用方向:控制、速度、时长、高动态、多主体驱动 类型工作基础模型WAN / WAN-VACE / HunyuanVideo控制条件轨迹控制ATI~镜头控制ReCamMaster~多主体驱动Phantom~音频驱动Let Them Talk: Audio-Driven Multi-Person Conversational Video Generation速…...
