什么是API网关?——驱动数字化转型的“隐形冠军”
什么是API网关
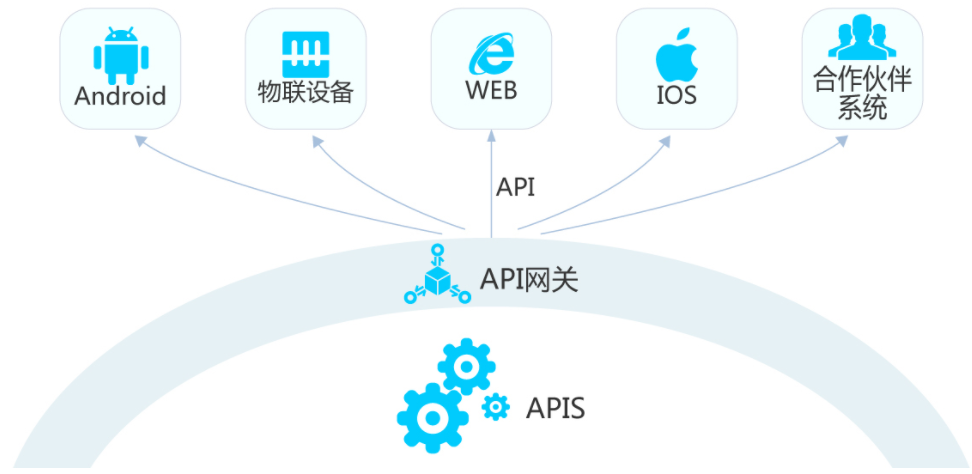
API网关(API Gateway)是一个服务器,位于应用程序和后端服务之间,提供了一种集中式的方式来管理API的访问。它是系统的入口点,负责接收并处理来自客户端的请求,然后将请求路由到相应的后端服务,并将结果返回给客户端。
在生活中我们使用的手机、物联设备和网页,都通过API实现设备与后端服务之间的连接与数据传输。而API网关除了负责处理请求和响应外,同时也具备了认证、限流、负载均衡等重要功能,依此来保障整个过程的安全、可靠和低延迟等。
API网关的出现背景
API网关的出现与微服务架构的发展密切相关。微服务架构是将一个大型的单个应用程序和服务拆分为数个甚至数十个支持微服务,每个微服务都是一个独立的个体,具有单独的数据库和部署环境,通过网络进行通信和协调,可以独立地进行开发、管理和迭代。这种架构方式使得API的数量大幅增加,同时带来以下这些问题:
-
客户端会多次请求不同的微服务,增加了客户端的复杂性;
-
认证和权限管控复杂,每个服务都需要独立认证和授权机制;
-
效率低,在跨越请求处理复杂业务时,无法保证请求的效率;
-
重构困难,随着业务需求的变更,可能会涉及到重新划分微服务。
API网关作为微服务架构中的一部分,负责处理这些挑战。它作为外部请求和内部服务之间的桥梁,对请求进行统一的路由、协议转换、安全控制和监控等操作。API网关的出现,会使得微服务架构更加灵活、可扩展,同时也简化了应用程序的开发和管理。
API网关能为企业做什么?
当今数字化时代,应用程序的构建和部署逐步复杂,微服务架构也逐步流行。在面对不同平台、客户端和服务的差异性需求时,API网关成为了现代应用程序的关键枢纽,也是企业数字化转型的不二之选,那API网关到底能为企业做些什么呢?
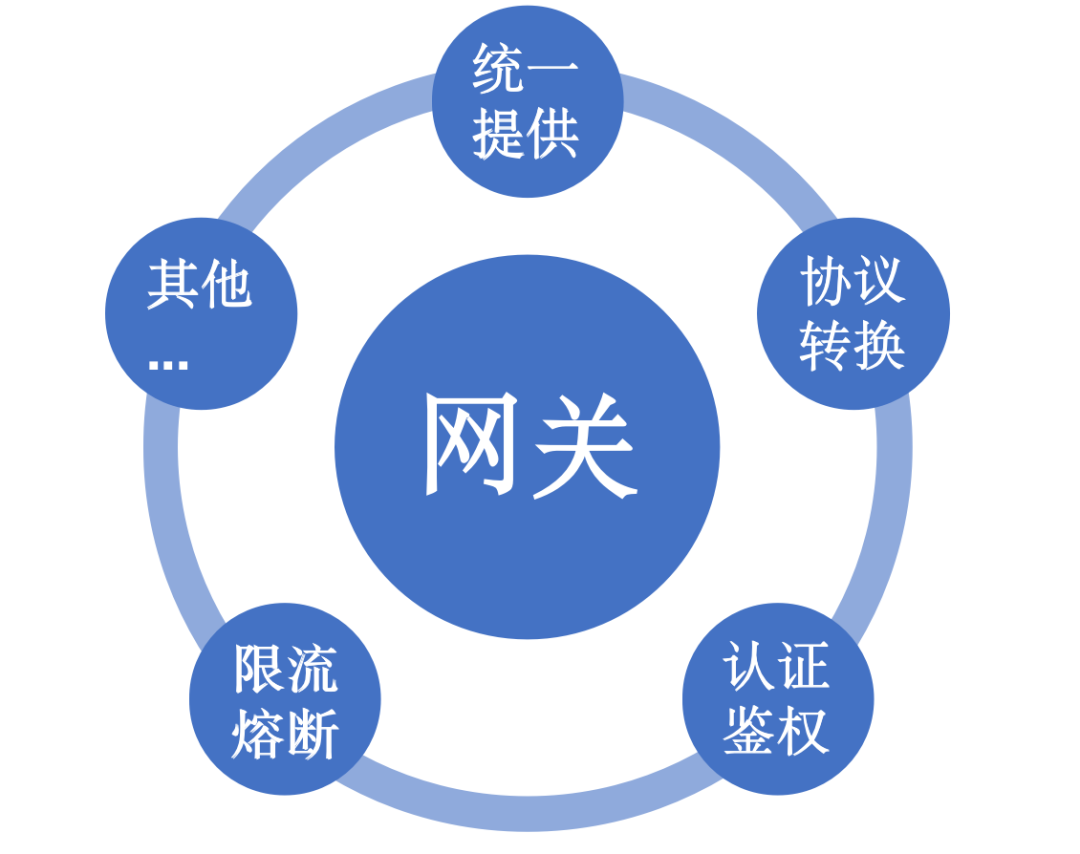
(1)统一对外接口
企业内部不同系统拥有不同的服务,接口由不同成员开发,在风格上会存在一定的差异,API网关可以统一服务差异并对外提供。当服务发生修改,可以通过API网关适配,不需要调用方进行调整,减少对外暴露服务数量,增加系统安全性。
(2)负载均衡
API网关可以依据服务的负载情况将请求分发到不同的服务实例,实现负载均衡。
(3)协议转换
API网关可以将不同协议的请求转换为后端服务可以处理的协议。例如,将HTTP请求转换为SOAP请求,以便后端服务可以处理。
(4)认证鉴权
API网关可以提供安全防护功能,例如身份验证、授权、防止恶意攻击等。通过在API网关设置安全策略,可以保护系统的安全性,防止未经授权的访问和数据泄露。
(5)限流熔断
API网关支持通过限制请求的速率或请求次数来实现流量控制。当后端服务出现故障时,API网关支持熔断机制,通过断开与服务之间的连接,避免请求堆积和系统崩溃。
相关文章:

什么是API网关?——驱动数字化转型的“隐形冠军”
什么是API网关 API网关(API Gateway)是一个服务器,位于应用程序和后端服务之间,提供了一种集中式的方式来管理API的访问。它是系统的入口点,负责接收并处理来自客户端的请求,然后将请求路由到相应的后端服…...
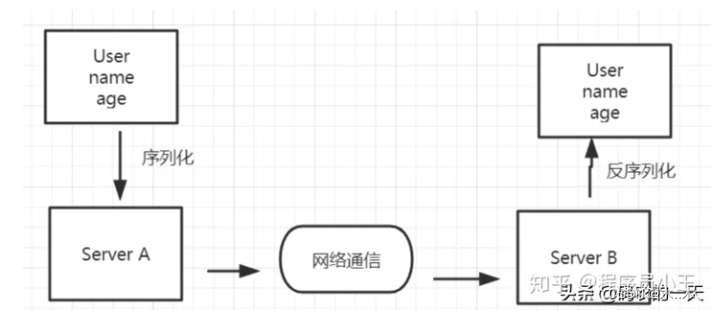
Java 序列化和反序列化为什么要实现 Serializable 接口?
序列化和反序列化 序列化:把对象转换为字节序列的过程称为对象的序列化. 反序列化:把字节序列恢复为对象的过程称为对象的反序列化. 什么时候需要用到序列化和反序列化呢或者对象序列化的两种用途… : (1) 对象持久化:把对象的…...

【【萌新的SOC学习之GPIO学习 水】】
萌新的SOC学习之GPIO学习 General Purpose I/O 通用I/O zynq-7000 SOC PS 分为四大部分 APU application Processor UintMemoryIO外设Interconnect 内部互联 PL : IO外设 GPIO可以连接通用的设备(比如按键) 也可以用GPIO模拟其他的协议 GP…...

10-Node.js入门
01.什么是 Node.js 目标 什么是 Node.js,有什么用,为何能独立执行 JS 代码,演示安装和执行 JS 文件内代码 讲解 Node.js 是一个独立的 JavaScript 运行环境,能独立执行 JS 代码,因为这个特点,它可以用来…...
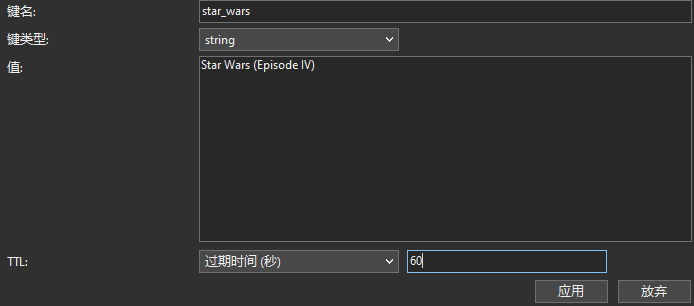
Redis 的过期键 | Navicat 技术干货
Redis 是一种高性能的内存数据存储,以其速度和多功能性而闻名。其中一个有用的特性是为键设置过期时间的功能。在 Redis 中,为键设置过期时间对于管理数据和确保过时或临时数据自动从数据库中删除是至关重要的。在本文中,我们将探讨在 redis-…...

IDC服务器商是如何保护服务器的数据安全
服务器是作为一个公司存储数据和管理服务的设备,随着网络的不断发展大数据的普遍性,所以数据安全问题也越来越受到企业和个体的重视,那么IDC服务器商家是如何对服务器的数据进行安全保护的呢? 配置防火墙。防火墙是服务器的必备工…...
c++中什么时候用double?
c中什么时候用double? 在C中,通常使用double数据类型来表示浮点数,特别是当需要更高的精度时。以下是一些情况下可以考虑使用double的示例: 1. **需要高精度的计算**:当您需要进行精确的浮点数计算时,double通常比flo…...

TCP/IP(四)TCP的连接管理(一)三次握手
一 tcp连接回顾 部分内容来自小林coding TCP篇 记录的目的: 亲身参与进来,加深记忆 ① 引入 前面我们知道: TCP 是面向连接 [点对点的单播]的、可靠的、基于字节流的传输层通信协议面向连接意味着:在使用TCP之前,通信双方必须先建立一…...
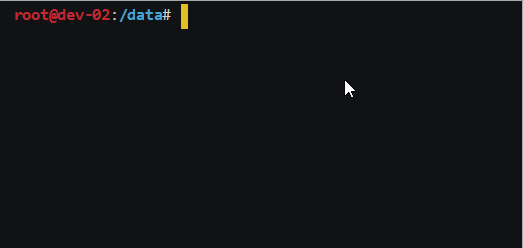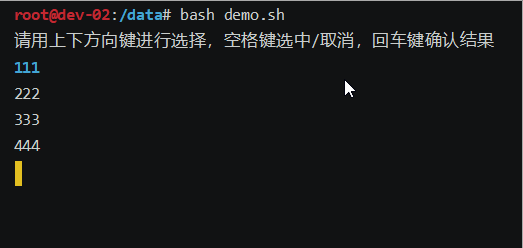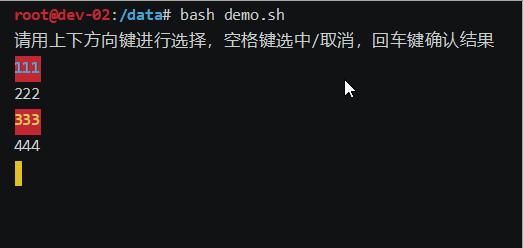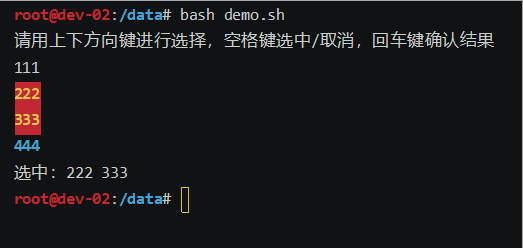
bash上下键选择选项demo脚本
效果如下: 废话不多说,上代码: #!/bin/bashoptions("111" "222" "333" "444") # 选项列表 options_index0 # 默认选中第一个选项 options_len${#options[]}echo "请用上下方向键进行选择&am…...

cf 1886A
题目是输入一个数字,分解成三个数字的和,这三个数字都不相同,并且都不可以被三整除,如果存在输出YES并且输出任意一组可能的三个数字,否则输出NO 代码 #include<bits/stdc.h> using namespace std;int main() …...

Spring5应用之事务属性
作者简介:☕️大家好,我是Aomsir,一个爱折腾的开发者! 个人主页:Aomsir_Spring5应用专栏,Netty应用专栏,RPC应用专栏-CSDN博客 当前专栏:Spring5应用专栏_Aomsir的博客-CSDN博客 文章目录 参考文献前言事务…...

C# 搭建一个简单的WebApi项目23.10.10
一、创建Web API 1、创建一个新的web API项目 启动VS 2019,并在“开始页”选择“创建新项目”。或从“文件”菜单选择“新建”,然后选择“项目”。 选择ASP.NET Web应用程序(.NET Framework) 2.点击下一步,到这个页面时选择Web API。 3.选中…...
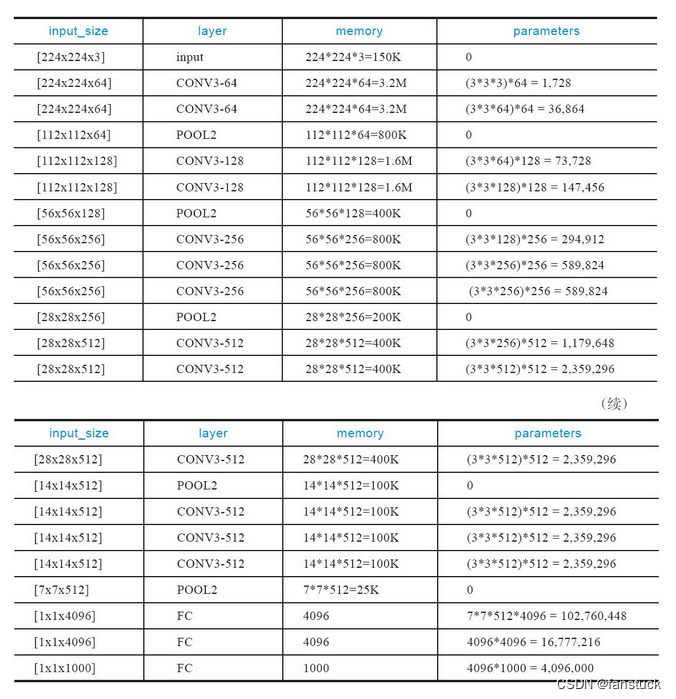
VGG卷积神经网络实现Cifar10图片分类-Pytorch实战
前言 当涉足深度学习,选择合适的框架是至关重要的一步。PyTorch作为三大主流框架之一,以其简单易用的特点,成为初学者们的首选。相比其他框架,PyTorch更像是一门易学的编程语言,让我们专注于实现项目的功能࿰…...

CentOS 7文件系统中的软链接和硬链接
软链接(Symbolic Link) 软链接,也称为符号链接,是一个指向另一个文件或目录的特殊类型的文件。它是一个指向目标文件的符号,就像快捷方式一样。软链接的创建和使用非常灵活,适用于各种情况。 创建软链接 …...
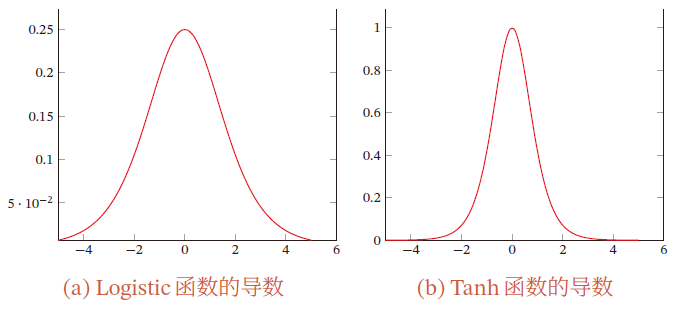
【AI】深度学习——前馈神经网络——全连接前馈神经网络
文章目录 1.1 全连接前馈神经网络1.1.1 符号说明超参数参数活性值 1.1.2 信息传播公式通用近似定理 1.1.3 神经网络与机器学习结合二分类问题多分类问题 1.1.4 参数学习矩阵求导链式法则更为高效的参数学习反向传播算法目标计算 ∂ z ( l ) ∂ w i j ( l ) \frac{\partial z^{…...
超简单的视频截取方法,迅速提取所需片段!
“视频可以截取吗?用相机拍摄了一段视频,但是中途相机发生了故障,录进去了很多不需要的片段,现在想截取一部分视频出来,但是不知道方法,想问问广大的网友,知不知道视频截取的方法。” 无论是工…...
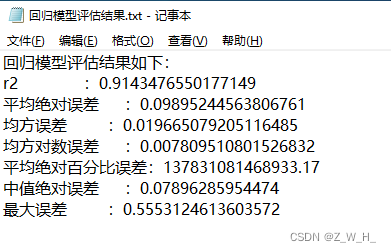
ArcGIS/GeoScene脚本:基于粒子群优化的支持向量机回归模型
参数输入 1.样本数据必须包含需要回归的字段 2.回归字段是数值类型 3.影响因子是栅格数据,可添加多个 4.随机种子可以确保每次运行的训练集和测试集一致 5.训练集占比为0-1之间的小数 6.迭代次数:迭代次数越高精度越高,但是运行时间越长…...

vue3组件的通信方式
一、vue3组件通信方式 通信仓库地址:vue3_communication: 当前仓库为贾成豪老师使用组件通信案例 不管是vue2还是vue3,组件通信方式很重要,不管是项目还是面试都是经常用到的知识点。 比如:vue2组件通信方式 props:可以实现父子组件、子父组件、甚至兄弟组件通信 自定义事件:可…...

Qt QPair
QPair 文章目录 QPair 摘要QPairQPair 特点代码示例QPair 与 QMap 区别 关键字: Qt、 QPair、 QMap、 键值、 容器 摘要 今天在观摩小伙伴撸代码的时候,突然听到了QPair自己使用Qt开发这么就,竟然都不知道,所以趁没有被人发…...
K8S云计算系列-(3)
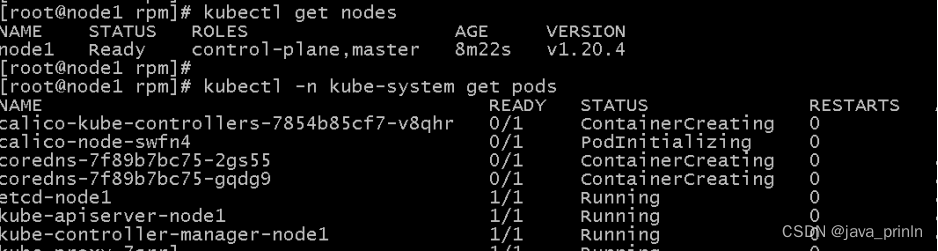
K8S Kubeadm案例实战 Kubeadm 是一个K8S部署工具,它提供了kubeadm init 以及 kubeadm join 这两个命令来快速创建kubernetes集群。 Kubeadm 通过执行必要的操作来启动和运行一个最小可用的集群。它故意被设计为只关心启动集群,而不是之前的节点准备工作…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...
。】2022-5-15)
【根据当天日期输出明天的日期(需对闰年做判定)。】2022-5-15
缘由根据当天日期输出明天的日期(需对闰年做判定)。日期类型结构体如下: struct data{ int year; int month; int day;};-编程语言-CSDN问答 struct mdata{ int year; int month; int day; }mdata; int 天数(int year, int month) {switch (month){case 1: case 3:…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...

【Redis技术进阶之路】「原理分析系列开篇」分析客户端和服务端网络诵信交互实现(服务端执行命令请求的过程 - 初始化服务器)
服务端执行命令请求的过程 【专栏简介】【技术大纲】【专栏目标】【目标人群】1. Redis爱好者与社区成员2. 后端开发和系统架构师3. 计算机专业的本科生及研究生 初始化服务器1. 初始化服务器状态结构初始化RedisServer变量 2. 加载相关系统配置和用户配置参数定制化配置参数案…...

pam_env.so模块配置解析
在PAM(Pluggable Authentication Modules)配置中, /etc/pam.d/su 文件相关配置含义如下: 配置解析 auth required pam_env.so1. 字段分解 字段值说明模块类型auth认证类模块,负责验证用户身份&am…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

《基于Apache Flink的流处理》笔记
思维导图 1-3 章 4-7章 8-11 章 参考资料 源码: https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...

分布式增量爬虫实现方案
之前我们在讨论的是分布式爬虫如何实现增量爬取。增量爬虫的目标是只爬取新产生或发生变化的页面,避免重复抓取,以节省资源和时间。 在分布式环境下,增量爬虫的实现需要考虑多个爬虫节点之间的协调和去重。 另一种思路:将增量判…...
