机器学习 - 似然函数:概念、应用与代码实例
目录
- 一、概要
- 二、什么是似然函数
- 数学定义
- 似然与概率的区别
- 重要性
- 举例
- 三、似然函数与概率密度函数
- 似然函数(Likelihood Function)
- 定义
- 例子
- 概率密度函数(Probability Density Function, PDF)
- 定义
- 区别与联系
- 四、最大似然估计(Maximum Likelihood Estimation, MLE)
- 定义与基本思想
- 例子与代码:估计正态分布的参数
- Python代码实现
- 输入与输出
- 处理过程
- 五、似然函数在机器学习中的应用
- 监督学习:逻辑回归
- 定义
- 例子与代码:逻辑回归模型
- 输入与输出
- 处理过程
- 六、总结
本文深入探讨了似然函数的基础概念、与概率密度函数的关系、在最大似然估计以及机器学习中的应用。通过详尽的定义、举例和Python/PyTorch代码示例,文章旨在提供一个全面而深入的理解。
关注TechLead,分享AI全维度知识。作者拥有10+年互联网服务架构、AI产品研发经验、团队管理经验,同济本复旦硕,复旦机器人智能实验室成员,阿里云认证的资深架构师,项目管理专业人士,上亿营收AI产品研发负责人。

一、概要
在机器学习和统计学领域中,似然函数(Likelihood Function)是一个至关重要的概念。它不仅是参数估计的基础,而且在模型选择、模型评估以及众多先进的算法和技术中都有着广泛的应用。本文旨在全面但深入地探讨似然函数,从其基本定义和性质到在不同机器学习问题中的具体应用。
文章将首先介绍似然函数与概率密度函数的关系,然后通过最大似然估计(Maximum Likelihood Estimation, MLE)来展示如何利用似然函数进行参数估计。接着,我们会探讨似然函数在分类问题和回归问题中的应用,并使用Python和PyTorch代码段进行示例演示。
为了保持文章的技术深度,我们还将讨论模型选择与似然比检验,以及似然函数在最新研究进展中的角色,如在贝叶斯方法和复杂模型优化中的应用。
二、什么是似然函数
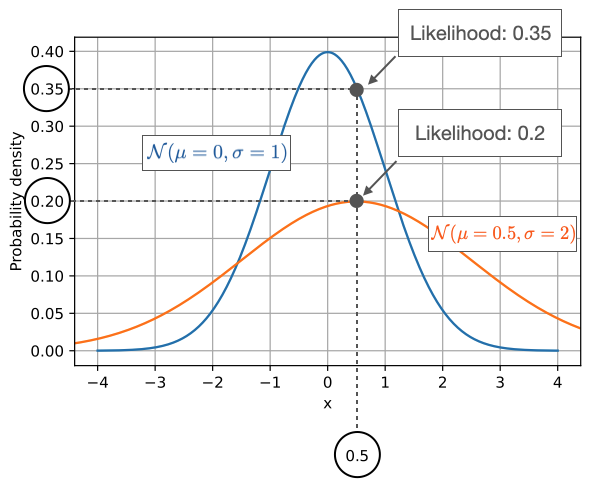
似然函数是一个在统计学和机器学习中经常出现的概念,它用于描述给定参数下,观察到某一数据样本的"可能性"。似然函数通常被记作 ( L(\theta \mid x) ),其中 ( \theta ) 是模型参数,( x ) 是观察到的数据。
数学定义
数学上,似然函数可以定义为:

似然与概率的区别
- 概率: 描述在固定的参数 ( \theta ) 下,某一事件 ( x ) 发生的可能性。
- 似然: 描述已经观察到事件 ( x ),而参数 ( \theta ) 是什么的可能性。
简单来说,概率是用来描述数据的生成模型,而似然是用来描述参数的合理性。
重要性
似然函数是许多统计推断方法的基础,包括但不限于:
- 最大似然估计(MLE)
- 贝叶斯推断
- 似然比检验
举例
考虑一个投掷硬币的例子,其中硬币正面出现的概率是 ( p ),反面出现的概率是 ( 1-p )。
若我们观察到了3次正面和2次反面,似然函数可以写作:

通过这一节,我们理解了似然函数的基础定义,区别和重要性,并通过一个简单的例子加深了理解。在接下来的部分,我们将更深入地探讨似然函数在机器学习和统计学中的应用。
三、似然函数与概率密度函数
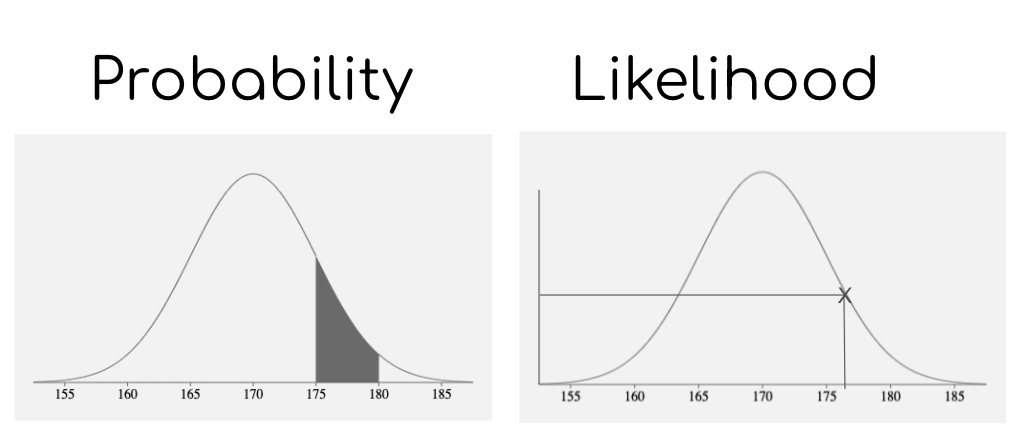
似然函数(Likelihood Function)和概率密度函数(Probability Density Function,简称PDF)都是描述数据和参数关系的重要数学工具。尽管两者在形式上具有相似性,它们在解释、用途和计算方面有着明显的不同。本节将详细介绍这两个概念的定义、区别和应用场景,并通过具体例子进行解释。
似然函数(Likelihood Function)
定义
似然函数用于量化在给定某参数值时,观察到某一数据样本的“可能性”。数学上,似然函数的定义如下:

例子
考虑一个简单的掷硬币实验,假设硬币正面出现的概率是 ( p )。若投掷了5次,出现了3次正面,2次反面。在这种情况下,似然函数可以表示为:

概率密度函数(Probability Density Function, PDF)
定义
概率密度函数描述了一个连续随机变量在各个特定值上的“密度”,也就是该值出现的相对可能性。对于离散随机变量,这个概念被称为概率质量函数(Probability Mass Function, PMF)。

区别与联系
- 角色互换: 在概率密度函数中,参数是固定的,我们考虑数据的变化。在似然函数中,数据是已知的,我们考虑参数的变化。
- 目的不同: 概率密度函数用于描述数据生成模型,而似然函数用于基于观察到的数据进行参数估计。
- 数学性质: 概率密度函数需要满足概率的公理(如非负性,积分(或求和)为1),而似然函数没有这样的要求。
四、最大似然估计(Maximum Likelihood Estimation, MLE)
最大似然估计是一种常用的参数估计方法,它通过最大化似然函数来找到最“合适”的参数值。在这一节中,我们将详细讲解最大似然估计的基础理论、应用场景,并通过具体的例子与代码演示进行解释。
定义与基本思想

例子与代码:估计正态分布的参数

Python代码实现
下面是使用Python和PyTorch来实现最大似然估计的代码。
import torch
import torch.optim as optim# 随机生成一些正态分布的数据样本(均值为5,标准差为2)
data = torch.normal(5, 2, size=(100,))# 初始化参数
mu = torch.tensor(1.0, requires_grad=True)
sigma = torch.tensor(1.0, requires_grad=True)# 优化器
optimizer = optim.SGD([mu, sigma], lr=0.01)# 迭代次数
n_iter = 5000# 开始优化
for i in range(n_iter):optimizer.zero_grad()# 计算负对数似然n = len(data)neg_log_likelihood = 0.5 * n * torch.log(2 * torch.tensor(3.14159)) + n * torch.log(sigma) + torch.sum((data - mu)**2) / (2 * sigma**2)# 反向传播neg_log_likelihood.backward()# 更新参数optimizer.step()# 输出结果
print(f"Estimated mu: {mu.data}")
print(f"Estimated sigma: {sigma.data}")
输入与输出
- 输入:一个来自正态分布的数据样本(
data)。 - 输出:估计得到的均值(
mu)和标准差(sigma)。
处理过程
- 初始化均值和标准差的参数。
- 使用梯度下降法来最小化负对数似然函数。
通过以上的定义、例子和代码,最大似然估计在参数估计中的重要性和实用性得以充分展示。在接下来的部分,我们将继续深入探讨如何使用似然函数进行更复杂的模型选择和评估。
五、似然函数在机器学习中的应用
似然函数不仅在统计推断中有重要应用,也在机器学习,尤其是在监督学习、非监督学习以及模型选择等方面有广泛的使用。本节将深入探讨似然函数在机器学习各领域中的应用,并提供相关的代码示例。
监督学习:逻辑回归
定义
在监督学习中,特别是用于分类问题的逻辑回归模型,最大似然估计用于优化模型的参数。逻辑回归模型试图找到一个函数,使得给定输入特征下某一类别出现的“可能性”最大。
例子与代码:逻辑回归模型

以下是用PyTorch实现逻辑回归模型的代码:
import torch
import torch.nn as nn
import torch.optim as optim# 创建一些简单的数据
x_data = torch.tensor([[1.0], [2.0], [3.0], [4.0]])
y_data = torch.tensor([[0], [0], [1], [1]], dtype=torch.float32)# 定义模型
class LogisticRegressionModel(nn.Module):def __init__(self):super(LogisticRegressionModel, self).__init__()self.linear = nn.Linear(1, 1)def forward(self, x):y_pred = torch.sigmoid(self.linear(x))return y_predmodel = LogisticRegressionModel()# 损失和优化器
criterion = nn.BCELoss()
optimizer = optim.SGD(model.parameters(), lr=0.01)# 训练模型
for epoch in range(1000):model.train()optimizer.zero_grad()y_pred = model(x_data)loss = criterion(y_pred, y_data)loss.backward()optimizer.step()# 输出训练后的参数
print("Weight:", model.linear.weight.item())
print("Bias:", model.linear.bias.item())
输入与输出
- 输入:特征 (x) 和标签 (y)。
- 输出:逻辑回归模型的参数。
处理过程
- 初始化模型和优化器。
- 使用二元交叉熵损失函数(对应于逻辑回归的负对数似然函数)。
- 通过梯度下降来更新模型的参数。
六、总结
在本篇博客中,我们从似然函数的基础概念出发,深入探讨了它在统计推断和机器学习中的多方面应用。无论是在参数估计的最大似然估计法,还是在逻辑回归和高斯混合模型中,似然函数都发挥着至关重要的作用。通过最大化似然函数,我们不仅能找到描述数据的“最合适”的模型参数,而且还可以更深入地理解模型的性质和限制。
-
似然函数与梯度下降:在机器学习中,尤其是深度学习领域,梯度下降是最常用的优化算法。然而,不同的损失函数(即负对数似然函数)可能导致不同的优化性能和模型泛化能力。理解似然函数如何与梯度下降算法交互,有助于我们更有效地训练模型。
-
模型选择与复杂度:在现实应用中,选择一个“最佳”模型通常涉及到复杂度与准确性之间的权衡。通过似然函数,我们可以更直观地评估模型复杂度与数据拟合度之间的关系,从而进行更合理的模型选择。
-
似然函数与不确定性:在现实世界的很多问题中,数据往往具有噪声和不确定性。似然函数为我们提供了一种量化不确定性的方式,进一步,我们甚至可以通过贝叶斯方法,将先验信息与似然函数相结合,以更全面地理解数据和模型。
-
似然函数与生成模型:在非监督学习和生成模型(如GANs)中,似然函数的概念有时会被重新定义或拓展,以适应更复杂或高维的数据结构。理解这些扩展或变种的数学基础,可以为研究和应用这些先进模型提供有力的支撑。
通过深入探讨似然函数和最大似然估计,本文旨在为读者提供一个全面而深入的理解,帮助大家更有效地应用这一概念于各种实际问题中。无论你是统计学家,还是机器学习研究者,甚至是工程师,理解和掌握似然函数都将是你走向专业化、高效解决问题之路上的重要一步。
关注TechLead,分享AI全维度知识。作者拥有10+年互联网服务架构、AI产品研发经验、团队管理经验,同济本复旦硕,复旦机器人智能实验室成员,阿里云认证的资深架构师,项目管理专业人士,上亿营收AI产品研发负责人。
相关文章:

机器学习 - 似然函数:概念、应用与代码实例
目录 一、概要二、什么是似然函数数学定义似然与概率的区别重要性举例 三、似然函数与概率密度函数似然函数(Likelihood Function)定义例子 概率密度函数(Probability Density Function, PDF)定义 区别与联系 四、最大似然估计&am…...

LeetCode 热题 100-49. 字母异位词分组
题目描述 给你一个字符串数组,请你将 字母异位词 组合在一起。可以按任意顺序返回结果列表。 字母异位词 是由重新排列源单词的所有字母得到的一个新单词。 示例 1: 输入: strs [“eat”, “tea”, “tan”, “ate”, “nat”, “bat”] 输出: [[“bat”],[“n…...

TensorFlow入门(十九、softmax算法处理分类问题)
softmax是什么? Sigmoid、Tanh、ReLU等激活函数,输出值只有两种(0、1,或-1、1或0、x),而实际现实生活中往往需要对某一问题进行多种分类。例如之前识别图片中模糊手写数字的例子,这个时候就需要使用softmax算法。 softmax的算法逻辑 如果判断输入属于某一个类的概率大于属于其…...

刷题用到的非常有用的函数c++(持续更新)
阅读导航 字符串处理类一、stoi()(将字符串转换为整数类型)二、to_string()(将整数类型转换为字符串类型)三、stringstream函数(将一个字符串按照指定的分隔符进行分词) 字符串处理类 一、stoi()ÿ…...

黑客技术(网络安全)——自学思路
如果你想自学网络安全,首先你必须了解什么是网络安全!,什么是黑客!! 1.无论网络、Web、移动、桌面、云等哪个领域,都有攻与防两面性,例如 Web 安全技术,既有 Web 渗透2.也有 Web 防…...

lNmp安装:
一、LNMP LNMP架构是目前成熟的企业网站应用模式之一,指的是协同工作的一整套系统和相关软件, 能够提供动态Web站点服务及其应用开发环境。LNMP是一个缩写词,具体包括Linux操作系统、nginx网站服务器、MySQL数据库服务器、 PHP(或…...
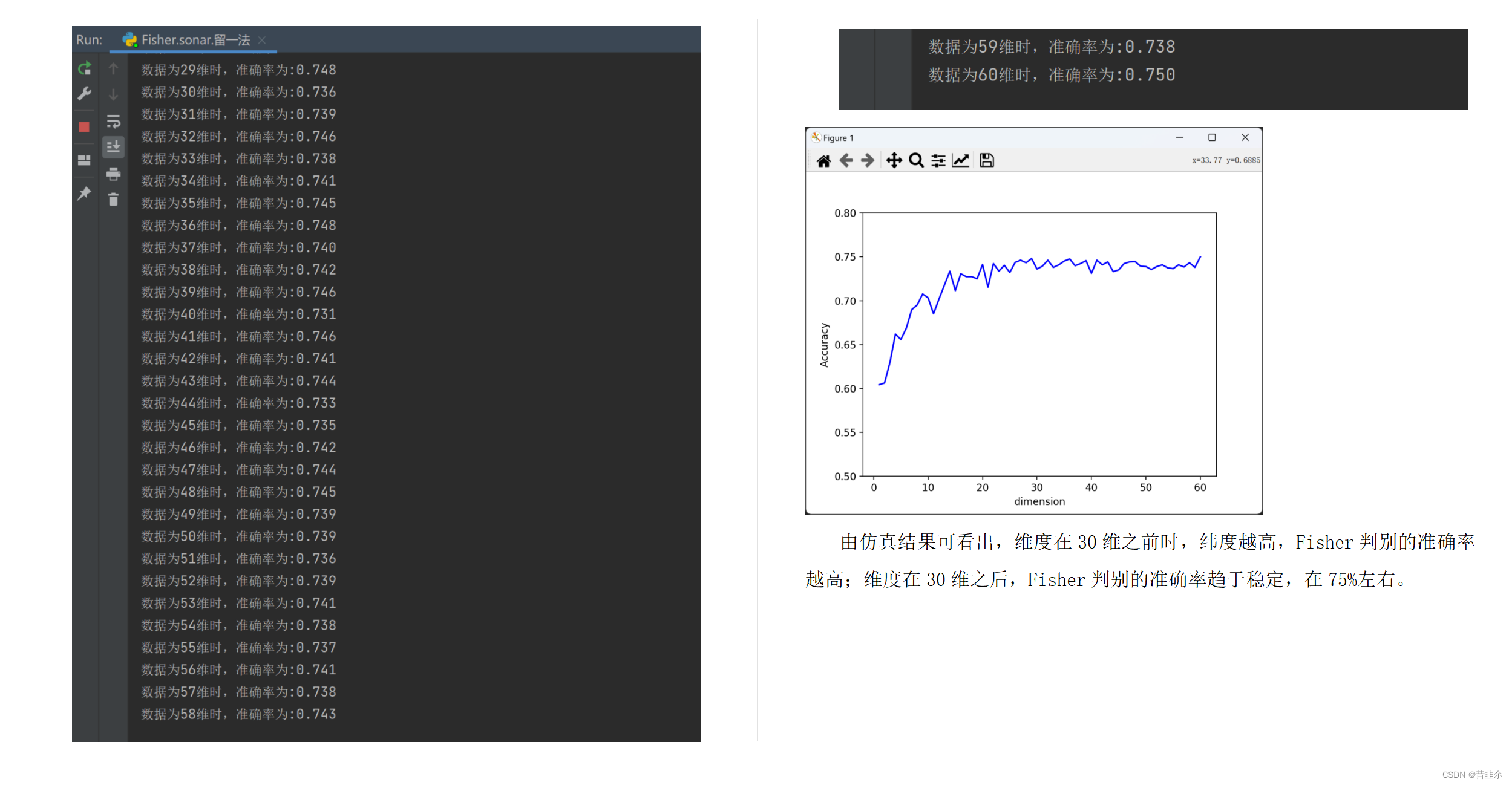
Fisher辨别分析
问题要求 在UCI数据集上的Iris和Sonar数据上验证算法的有效性。训练和测试样本有三种方式(三选一)进行划分: (一) 将数据随机分训练和测试,多次平均求结果 (二)K折交叉验证 &…...
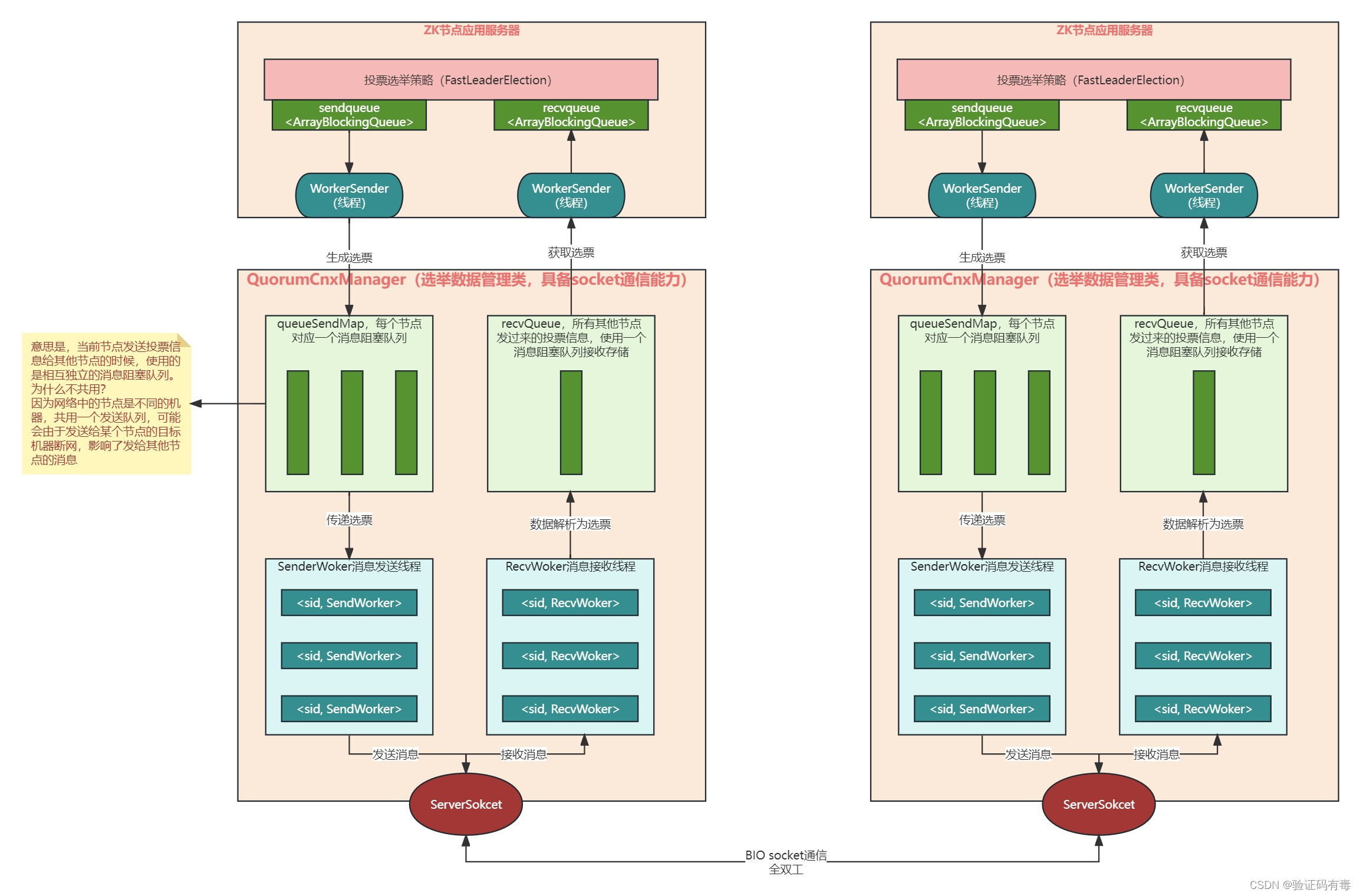
【Zookeeper专题】Zookeeper选举Leader源码解析
目录 前言阅读建议课程内容一、ZK Leader选举流程回顾二、源码流程图三、Leader选举模型图 学习总结 前言 为什么要看源码?说实在博主之前看Spring源码之前没想过这个问题。因为我在看之前就曾听闻大佬们说过【JavaCoder三板斧:Java,Mysql&a…...
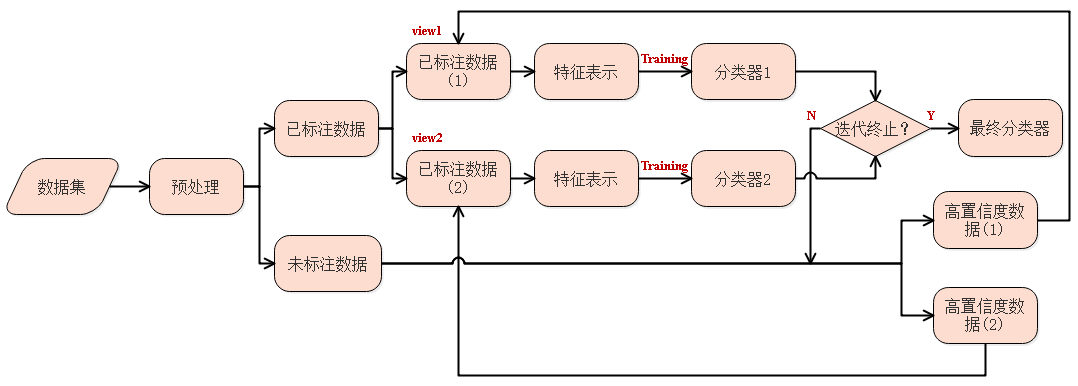
机器学习之自训练协同训练
前言 监督学习往往需要大量的标注数据, 而标注数据的成本比较高 . 因此 , 利用大量的无标注数据来提高监督学习的效果有着十分重要的意义. 这种利用少量标注数据和大量无标注数据进行学习的方式称为 半监督学习 ( Semi…...

ubuntu 通过apt-get快速安装 docker
在使用 apt-get 安装 Docker 之前,你需要确保你的系统已经准备好并且已经更新了软件包列表。以下是在 Ubuntu 系统上使用 apt-get 安装 Docker 的步骤: 更新软件包列表: sudo apt-get update 安装依赖软件包,以确保可以通过 HTTPS 使用存储库: sudo apt-get install apt-t…...
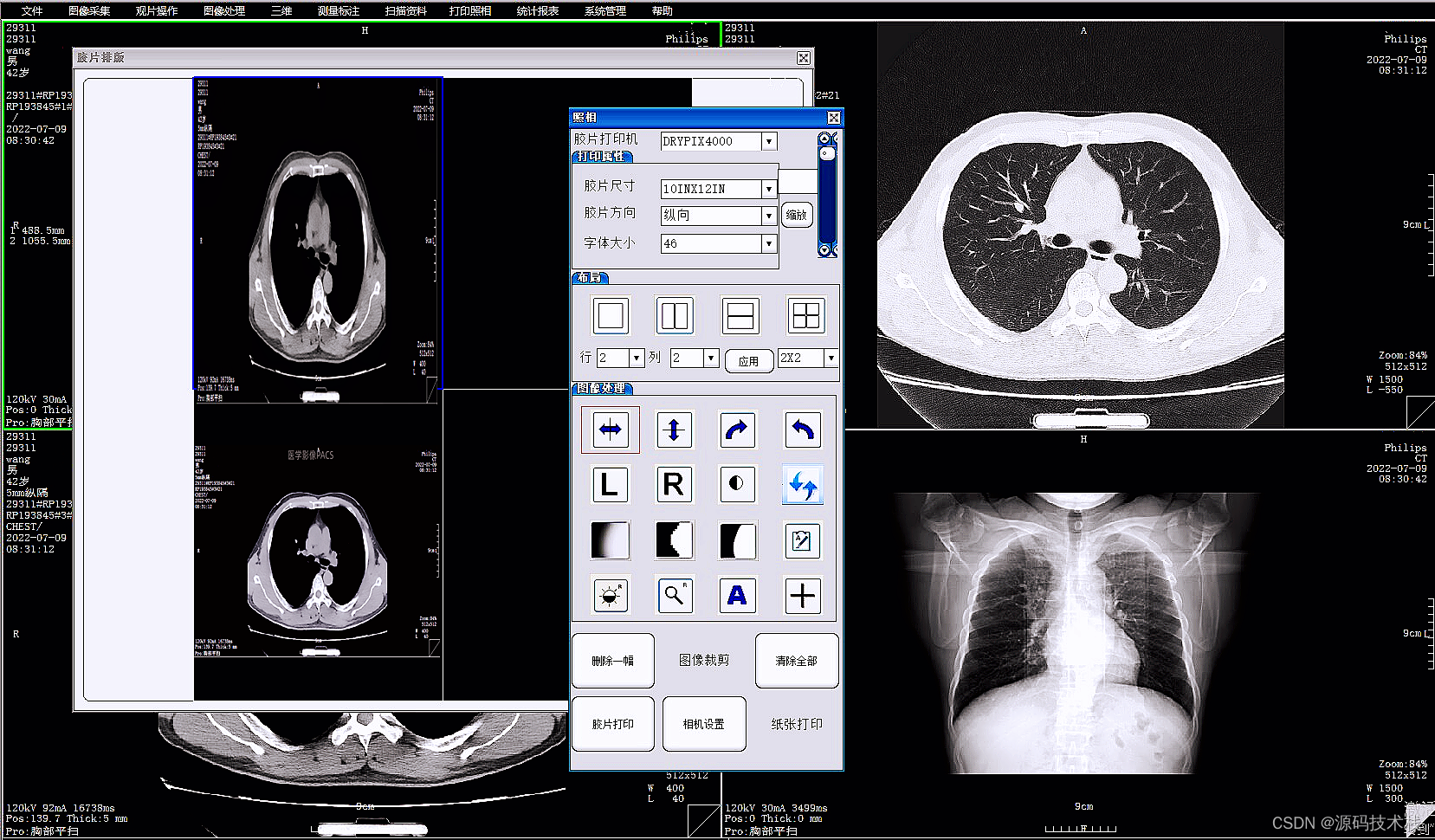
C++医院影像科PACS源码:三维重建、检查预约、胶片打印、图像处理、测量分析等
PACS连接DICOM接口的医疗器械(如CT、MRI、CR、DR、DSA、各种窥镜成像系统设备等),实现图像无损传输,实现DICOM胶片打印机回传打印功能,支持各种图像处理,可以进行窗技术调节,与登记台管理系统共…...

企业聊天应用程序使用 Kubernetes
1. 客户端-服务器工作流程 客户端:在我们的架构中,客户端可以分为三种类型:iOS 和 Android 移动应用程序以及 Web 聊天。移动应用程序首先通过 API 网关服务与服务器进行通信,其中客户端会生成一个访问令牌,该令牌将授…...
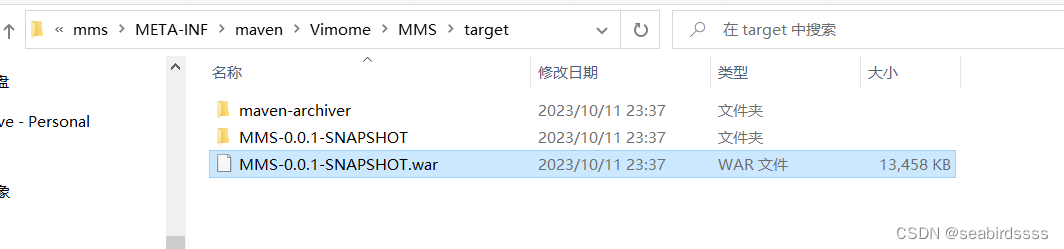
记录用命令行将项目打包成war包
记录用命令行将项目打包成war包 找到项目的pom.xml 在当前路径下进入cmd 输入命令 mvn clean package 发现报错了 Failed to execute goal org.apache.maven.plugins:maven-war-plugin:2.2:war (default-war) on project MMS: Error assembling WAR: webxml attribute is req…...

Linux基础知识笔记
Linux基础知识笔记 介绍/dev/null作用2>&1作用 介绍 记录linux基础知识,持续更新中… /dev/null作用 /dev/null 是一个特殊的设备文件,可以将数据重定向到这个文件中,从而实现将输出或错误信息丢弃的效果。在 Linux 系统中…...

Laya3.0 入门教程
点击play箭头 点击右边的开发者工具 就会弹出 chrome的调试窗口 然后定位到你自己的ts文件 直接在ts里断点即可 不需要js文件 如何自动生成代码? 比如你打开一个新项目 里面显示的是当前场景 只需要点击 UI运行时 右边的框就可以了 他会自动弹窗提示你 创建一个文…...

3D全景虚拟样板间展销系统扩展用户市场范围
VR样板间,能够真实还原现场,定制需要的场景。让一切比真实更真实。用户可以720度看房,自由行走在空间里,直观感受各空间的大小,看到自己家中的“未来样子”,同时通过操控手柄,控制整个智能家居系…...

如何编写lua扩展库
很多人都听过lua,也见过lua脚本,但可能不理解为什么lua脚本里面会有这么多没见过的函数, 而且这些函数功能是如此强大,能上天入地,无所不能 其实这些函数并不是lua自带的,都是由程序作者造出来的隐藏在了他们的主程序里 一般运行lua脚本,我们会使用自带的解释器,当你拿到一份…...
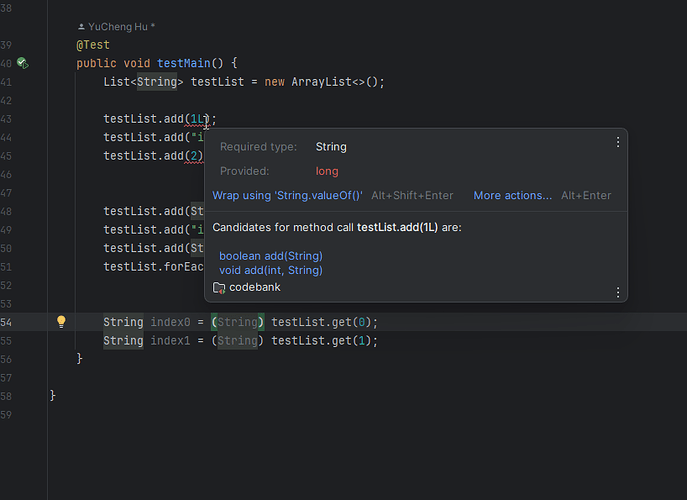
Java List 中存不同的数据类型
在最近的实践中,有人突然问了一个问题: 在 Java 的 List 中可以存不同的数据类型吗? 这个问题突然给问到了,我们都知道 Java 中的 List 中存的是对象,通常我们定义都会这样的定义: List<String> t…...

pyqt5:openpyxl 读取 Excel文件,显示在 QTableWidget 中
pip install openpyxl openpyxl-3.1.2-py2.py3-none-any.whl (249 kB) et_xmlfile-1.1.0-py3-none-any.whl (4.7 kB) 摘要:A Python library to read/write Excel 2010 xlsx/xlsm files pip install pyqt5; pip install pyqt5-tools; 编写 openpyxl_pyqt5.py 如…...

在RabbitMQ中使用新的MQTT 5.0功能
MQTT是物联网(IoT)的标准协议,是轻量级的,协议头很小,可以节省网络带宽。MQTT也很有效,与其他消息传递协议相比,客户端通过更短的握手进行连接和身份验证。 以下是本文介绍的MQTT 5.0功能列表&…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...

C++ 设计模式 《小明的奶茶加料风波》
👨🎓 模式名称:装饰器模式(Decorator Pattern) 👦 小明最近上线了校园奶茶配送功能,业务火爆,大家都在加料: 有的同学要加波霸 🟤,有的要加椰果…...

全面解析数据库:从基础概念到前沿应用
在数字化时代,数据已成为企业和社会发展的核心资产,而数据库作为存储、管理和处理数据的关键工具,在各个领域发挥着举足轻重的作用。从电商平台的商品信息管理,到社交网络的用户数据存储,再到金融行业的交易记录处理&a…...

Java 与 MySQL 性能优化:MySQL 慢 SQL 诊断与分析方法详解
文章目录 一、开启慢查询日志,定位耗时SQL1.1 查看慢查询日志是否开启1.2 临时开启慢查询日志1.3 永久开启慢查询日志1.4 分析慢查询日志 二、使用EXPLAIN分析SQL执行计划2.1 EXPLAIN的基本使用2.2 EXPLAIN分析案例2.3 根据EXPLAIN结果优化SQL 三、使用SHOW PROFILE…...

webpack面试题
面试题:webpack介绍和简单使用 一、webpack(模块化打包工具)1. webpack是把项目当作一个整体,通过给定的一个主文件,webpack将从这个主文件开始找到你项目当中的所有依赖文件,使用loaders来处理它们&#x…...
