【深蓝学院】手写VIO第7章--VINS初始化和VIO系统--笔记
0. 内容

1. VIO回顾
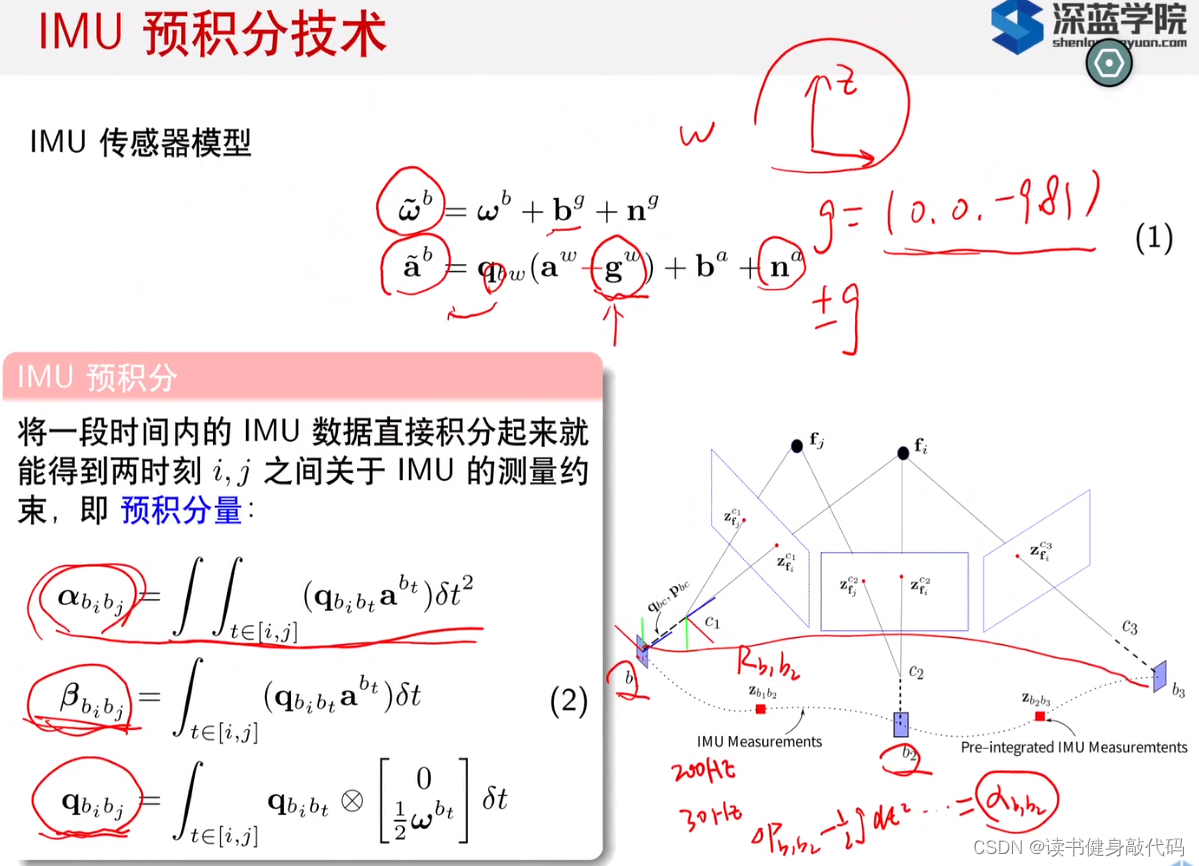
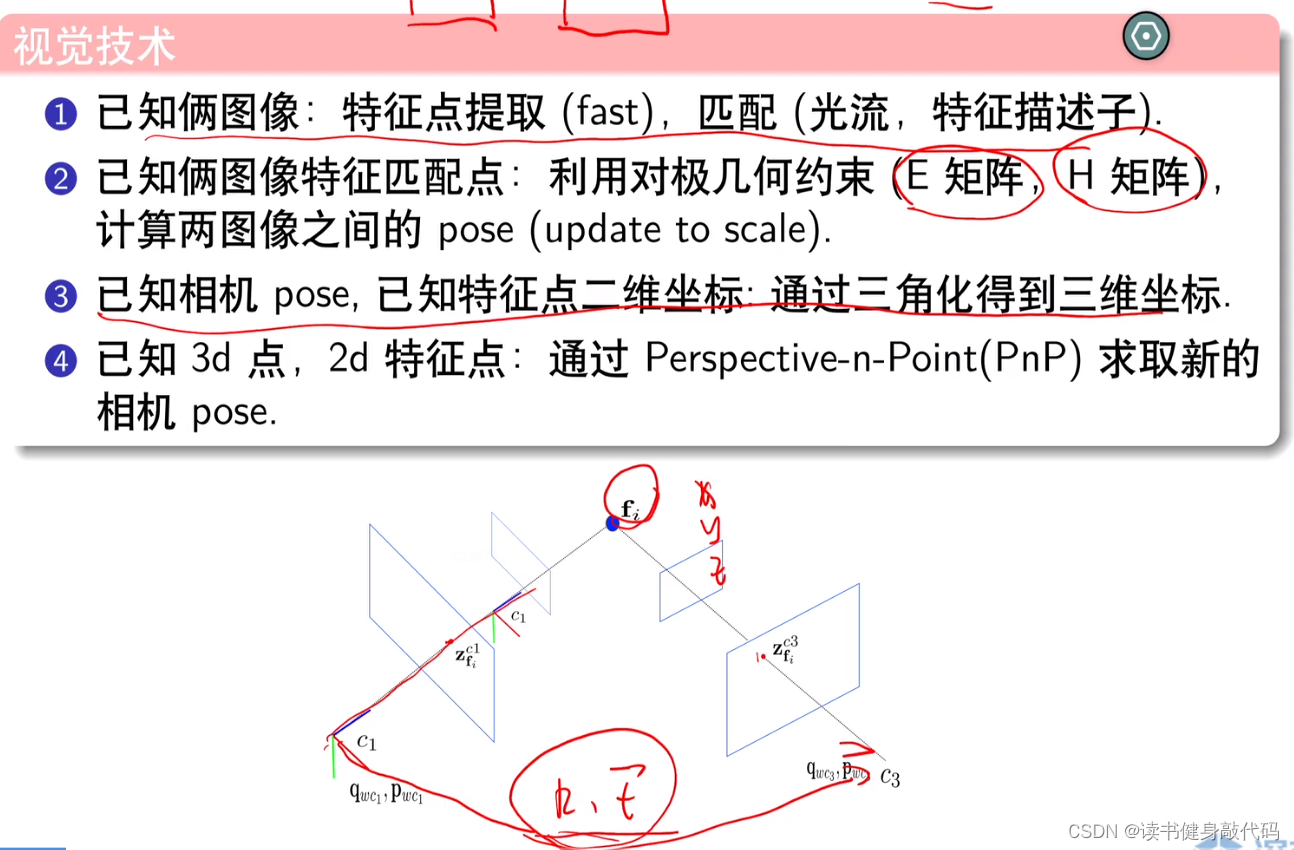
整个视觉前端pipeline回顾:
- 两帧图像,可提取特征点,特征匹配(描述子暴力匹配或者光流)
- 已知特征点匹配关系,利用几何约束计算relative pose([R|t]),translation只有方向,没有尺度
- 使用三角化获得3维坐标,即可完成vslam系统的初始化
- 有了3D特征点,后续可根据特征跟踪,使用PnP求解Camera Pose,无需再使用几何约束
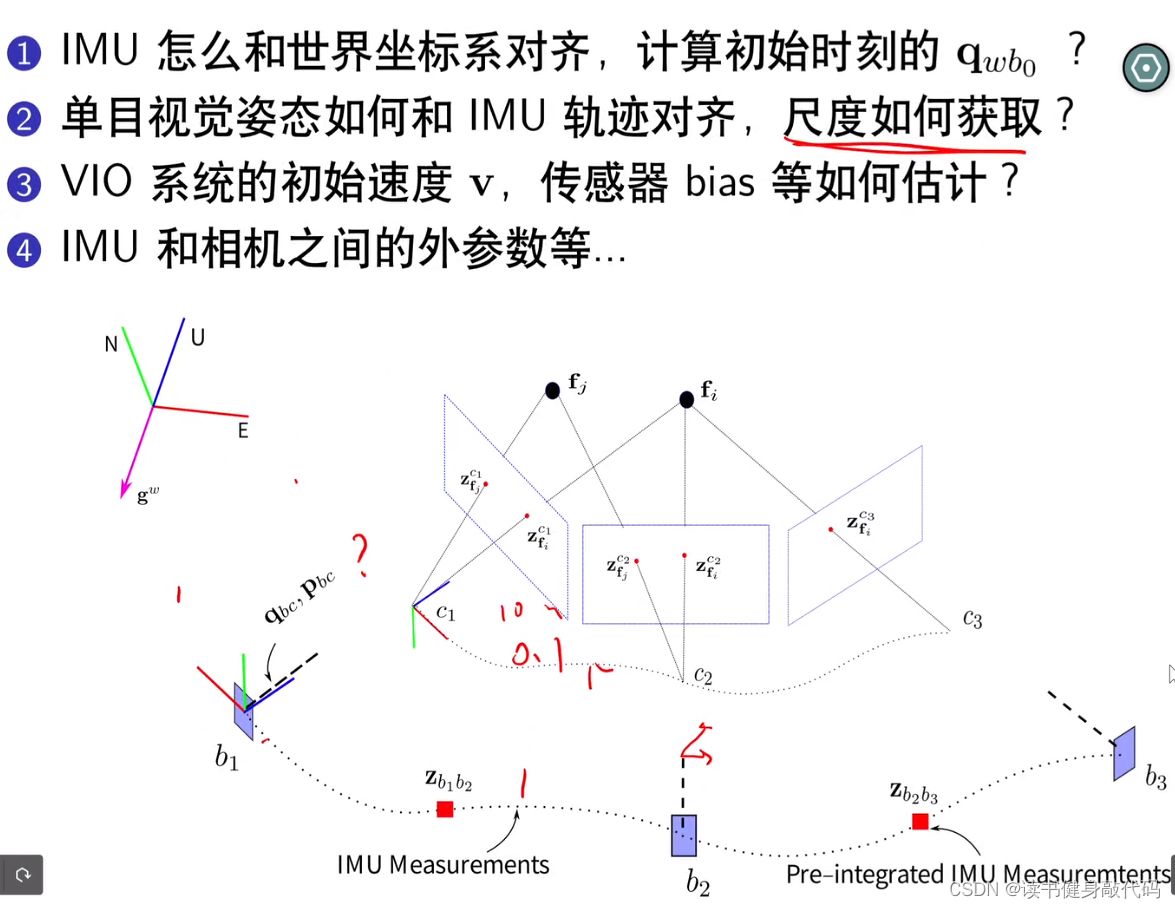
-
IMU的加速度要和世界系的重力进行对齐

世界系重力假设(0,0,-9.81),IMU第一帧估计出一个 c g = c R c b g b ^{c}g=^{c}R_{cb}g_b cg=cRcbgb,就可以求出第一帧camera在world下的pose(带头大哥) -
视觉的尺度和IMU尺度要进行对齐
-
VIO系统速度,传感器bias需要估计
-
IMU和相机的外参Tic
知道了z轴的法向量就能估计roll和pitch(tilt),但是yaw不可观。
2. VINS鲁棒初始化
2.1 pipeline overview
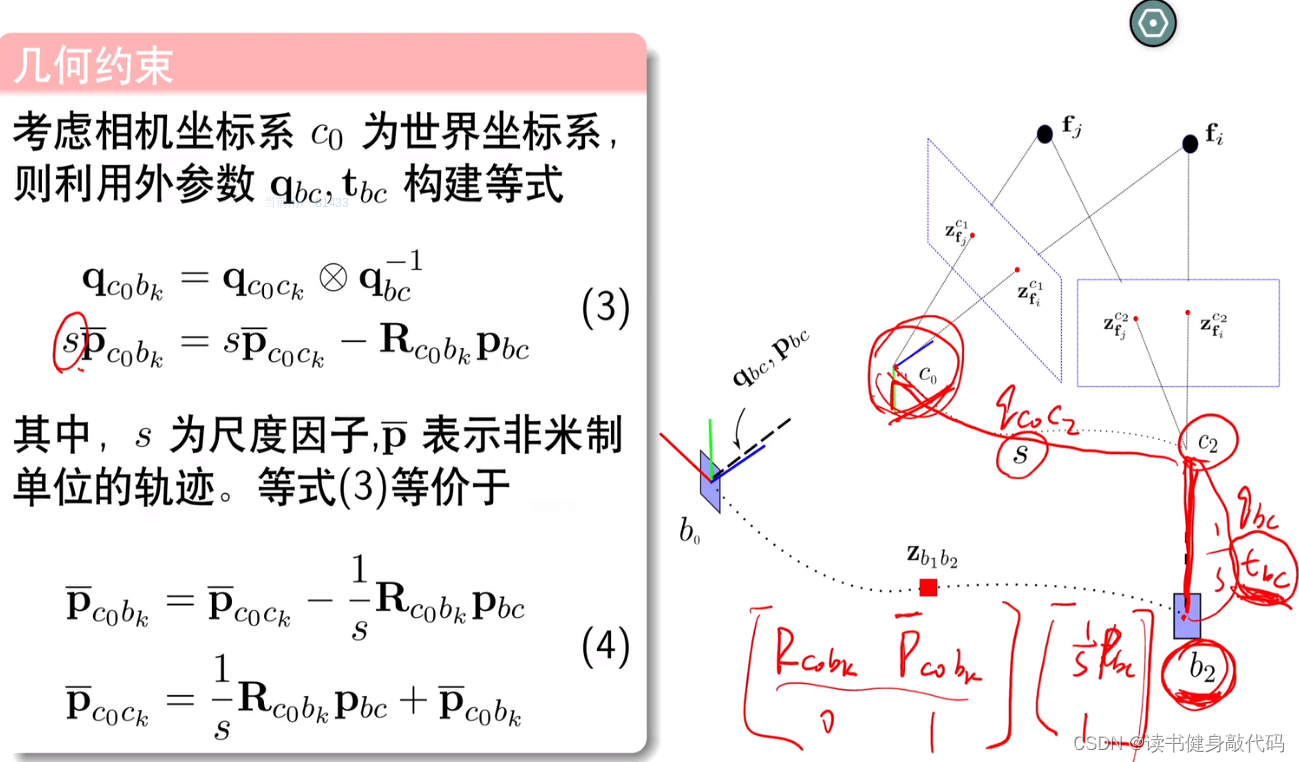
IMU积分是米制单位,但是camera不是,camera存在一个缩放因子,标定出外参 [ R b c , t b c ] [R_{bc},t_{bc}] [Rbc,tbc]之后,可以求得尺度因子s,先对坐标系,R,t的数学表示做一下说明:
旋转脚标相连时相消,刚性连接在不同时刻的的观测相同,平移左上角是观测系,右下角从左到右;平移乘旋转后平移向量不变,但观测系改变。
式(4)第一行这样理解:
c 0 p ‾ c 0 b k = c 0 p ‾ c 0 c k − 1 s c 0 R c 0 b k b p b c ( 2.1 ) {^{c_0}\overline p_{c_0b_k}}={^{c_0}\overline p_{c_0c_k}}-\frac{1}{s}{^{c_0} R_{c_0b_k}} {^{b}p_{bc}} (2.1) c0pc0bk=c0pc0ck−s1c0Rc0bkbpbc(2.1)
左上角都是观测系,即在什么系下看这个量,由于刚性连接在不同观测系,不同时间下相同,且平移乘旋转后旋转向量不变,但观测系改变,所以 b p b c = b k p b k c k ( 2.2 ) {^{b}p_{bc}}={^{b_k}p_{b_kc_k}}(2.2) bpbc=bkpbkck(2.2)
所以将(2.2)带入式(2.1)可得:
c 0 p ‾ c 0 b k = c 0 p ‾ c 0 c k − c 0 p ‾ b k c k = c 0 p ‾ c 0 c k + c 0 p ‾ c k b k ( 2.3 ) {^{c_0}\overline p_{c_0b_k}}={^{c_0}\overline p_{c_0c_k}}-{^{c_0}\overline p_{b_kc_k}}={^{c_0}\overline p_{c_0c_k}}+{^{c_0}\overline p_{c_kb_k}}(2.3) c0pc0bk=c0pc0ck−c0pbkck=c0pc0ck+c0pckbk(2.3)
即在 c 0 c_0 c0系下进行将 c 0 p ‾ c 0 c k + c 0 p ‾ c k b k {^{c_0}\overline p_{c_0c_k}}+{^{c_0}\overline p_{c_kb_k}} c0pc0ck+c0pckbk向量相加,不难理解。
标定出Camera和IMU外参之后,利用式(2.1)就可以求出尺度因子。

Tbc外参的Rotation很重要,而Translation由于可能离得比较近,所以相对来说没有Rotation重要
2.2 外参估计
旋转约束:两种路径求取的 q c k b k + 1 q_{c_kb_{k+1}} qckbk+1应该相同。

这里的未知量只有外参 q b c q_{bc} qbc,也可以简单地理解为一段时间内,camera出一段pose(trajectory),imu积分出一段pose(trajectory),这两段pose理想情况下只有外参的差异,(不考虑 t b c t_{bc} tbc的情况下)可以将这两段pose align起来,残差是两段pose align的残差,待估计量就是外参,做LSP的结果就是外参。

VINS论文中将多个时刻的数据累计起来,并使用了鲁棒核函数对每一项进行了加权,权值计算方法:有 t r ( R ) = 1 + 2 c o s θ tr(R)=1+2cos\theta tr(R)=1+2cosθ(可以看wiki),式(9)中的那一大块矩阵就是式(5)移项而得,因为求的是相同的量(如 q c k b k + 1 q_{c_kb_{k+1}} qckbk+1),所以理想情况下连乘应该是Identity,但实际上,如果外参估的不准,这个角度会较大(>threshole),所以式(8)将大于threshold的部分的权值设的较小,进行了抑制。
最终对 q b c q_{bc} qbc的求解还是对式(7)使用SVD分解,取 V T V^T VT最后一列作为解。
(参考这篇博客参考这篇博客中使用Lanrange算子证明取 V T V^T VT最后一列是我们所求的解。)
论文中还对SVD分解的倒数第二小奇异值进行了判断,如果小于阈值则认为该次估计无效,重新采集数据进行估计。(这和增多数据来提升数据信噪比是一样的目的,都是为了提高数值稳定性)
2.3 gyro bias估计

式(10)就是将 b k b_k bk到 b k + 1 b_{k+1} bk+1时刻之间imu的rotation都转到 c 0 c_0 c0系下进行align:
- 前两项四元数相乘代表求在 c 0 c_0 c0系下看imu在 b k b_k bk到 b k + 1 b_{k+1} bk+1时刻之间的relative rotation
- 第3项 q b k b k + 1 q_{b_kb_{k+1}} qbkbk+1是IMU积分而来的两时刻间的relative rotation真值(会受到gyro bias的影响),对其进行一阶Taylor展开,带入(10),(10)即代表一阶项所代表的 θ e r r \theta_{err} θerr,可以求出gyro bias
这跟前面估计外参的是一样的,都是使用的旋转约束。
2.4 初始化速度,重力,尺度因子

相关文章:

【深蓝学院】手写VIO第7章--VINS初始化和VIO系统--笔记
0. 内容 1. VIO回顾 整个视觉前端pipeline回顾: 两帧图像,可提取特征点,特征匹配(描述子暴力匹配或者光流)已知特征点匹配关系,利用几何约束计算relative pose([R|t]),translation只有方向&…...

大开眼界:Netbios 上古时代如何用一个参数实现一个世界 负面典型
今天的程序员普遍遵循这样的接口设计原则:通过不同的接口名和参数列表准确表达不同的功能。 这似乎是理所当然的,然而上古时代却并非如此,比如Netbios协议整个协议的接口只有一个函数、一个参数! 当初是基于什么原则这样设计不晓得…...

el-table制作表格,改变表格的滚动条样式
// 改变滚动条相关样式 *::-webkit-scrollbar {width:10px; height:0px; background-color:transparent;} /*定义滚动条高宽及背景 高宽分别对应横竖滚动条的尺寸*/ *::-webkit-scrollbar-track {background-color: rgba(0,0,0,0.3); } /*定义滚动条轨道 内阴影圆角*/ *::-web…...

Cmd报错:No module named ‘pip’
目录 1、问题描述2、问题原因3、问题解决 1、问题描述 今天在cmd命令行安装Twisted的扩展包whl文件时报错: ...... ModuleNotFoundError: No module named pip2、问题原因 升级pip时命令使用错误 3、问题解决 1) 重装pip python -m ensurepip2&#x…...

python输出奇数:如何使用Python输出奇数?
Python输出奇数的方法有很多种,下面给出一种使用for循环的实现方式:上述代码的输出结果为: Python输出奇数的方法有很多种,下面给出一种使用for循环的实现方式: # 定义一个变量n,表示要输出的奇数的最大值…...
2023 NewStarCTF --- wp
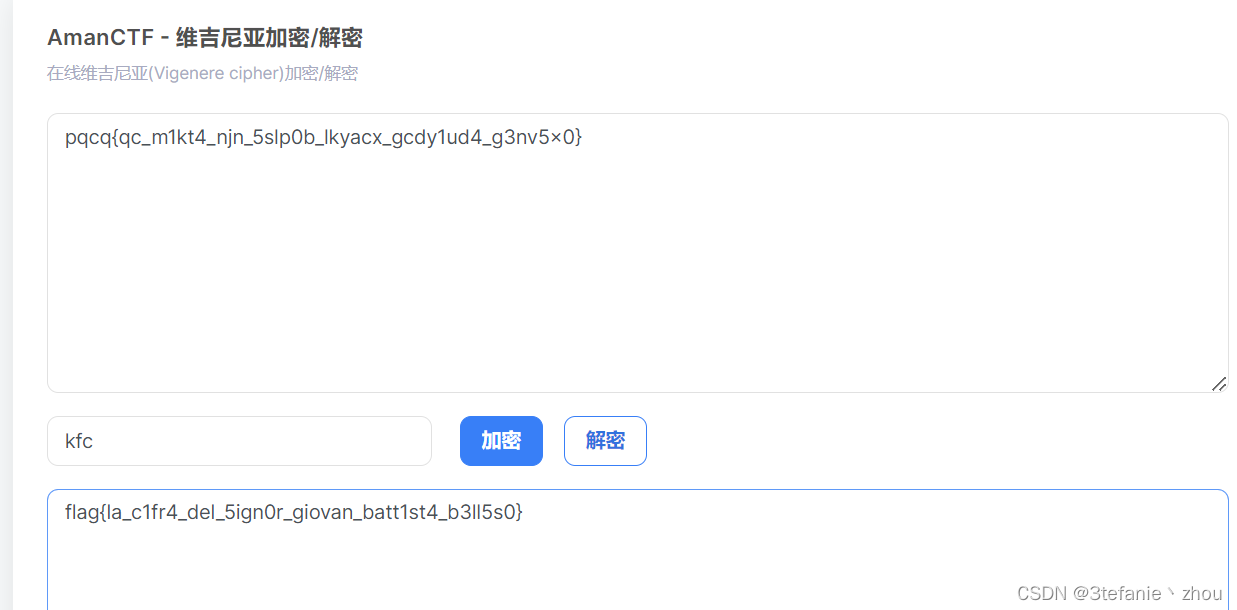
文章目录 前言Week1MiscCyberChefs Secret机密图片流量!鲨鱼!压缩包们空白格隐秘的眼睛 Web泄露的秘密Begin of UploadErrorFlaskBegin of HTTPBegin of PHPR!C!E!EasyLogin CryptobrainfuckCaesars SecertfenceVigenrebabyrsaSmall dbabyxorbabyencodin…...

一键切换IP地址:电脑IP更改的简便方法
今天我要和大家分享一个电脑IP更改的简便方法——一键切换IP地址。如果您想要更改电脑的IP地址,无需繁琐的设置和复杂的步骤,只需使用以下简单的方法,即可轻松实现IP地址的切换。让我们开始吧! 1、使用批处理脚本 批处理脚本是一…...

计算机相关内容的网站主题说明书
1. 网站名称: 中职计算机学堂 2. 网站目标: 主要目标:为中职学生提供计算机基础教程、编程入门、IT技能培训。次要目标:鼓励学生发表自己的作品,交流技术问题,构建IT爱好者社区。 3. 目标受众࿱…...
zabbix监控项
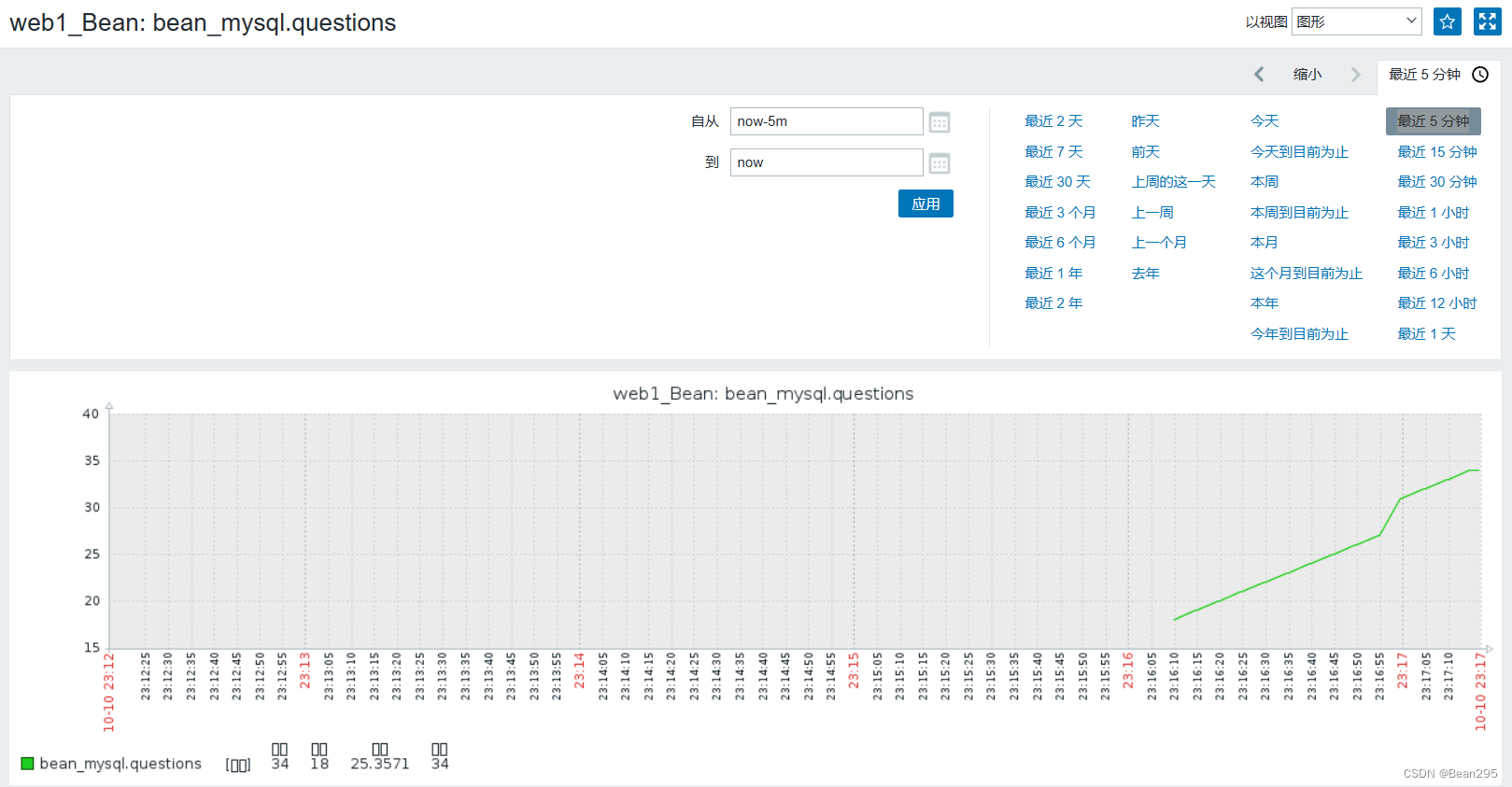
一、监控项(items) 1、获取监控数据的方式: ① zabbix-agent:代理程序是在被监控主机上运行的软件,负责收集和报告有关主机性能和状态的数据,监控系统通过与代理程序通信来获取数据。 ② SNMP࿱…...

Java基础面试-重载和重写的区别
重载:发生在同一个类中,方法名必须相同,参数类型不同、个数不同、顺序不同,方法返回值和访问修饰符可 以不同,发生在编译时。 重写:发生在父子类中,方法名、参数列表必须相同,返回值范围小于等于父类&…...

记一次生产大对象及GC时长优化经验
最近在做一次系统整体优化,发现系统存在GC时长过长及JVM内存溢出的问题,记录一下优化的过程 面试的时候我们都被问过如何处理生产问题,尤其是线上oom或者GC调优的问题更是必问,所以到底应该如何发现解决这些问题呢,用真实的场景实操ÿ…...

Vue项目为页面添加水印效果
最近在做项目,有这样要求,需要在指定容器中添加水印,也可不设置容器,如果没有容器,则添加在整个页面中,即body,当接到这个需求的时候我第一想的方法就是用canvas来实现,话不多说搞起…...

两数之和
给定一个整数数组 nums 和一个整数目标值 target,请你在该数组中找出 和为目标值 target 的那 两个 整数,并返回它们的数组下标。 你可以假设每种输入只会对应一个答案。但是,数组中同一个元素在答案里不能重复出现。 你可以按任意顺序返回…...

试过GPT-4V后,微软写了个166页的测评报告,业内人士:高级用户必读
一周之前,ChatGPT迎来重大更新,不管是 GPT-4 还是 GPT-3.5 模型,都可以基于图像进行分析和对话。与之对应的,多模态版GPT-4V模型相关文档也一并放出。当时 OpenAI 放出的文档只有18页,很多内容都无从得知,对…...

使用Python构造VARIMA模型
简介 VARMA(p,q)结合了VAR和VMA模型,其中p是向量自回归(VAR)模型的滞后期数,q是VMA模型的移动平均的阶数。 VARMA是ARMA的推广,它将ARMA模型扩展到多个时间序列变量的情况,通过VAR和VMA的线性组合来描述多个时间序列变量之间的联…...
Java基于SpringBoot+Vue的考研资讯平台
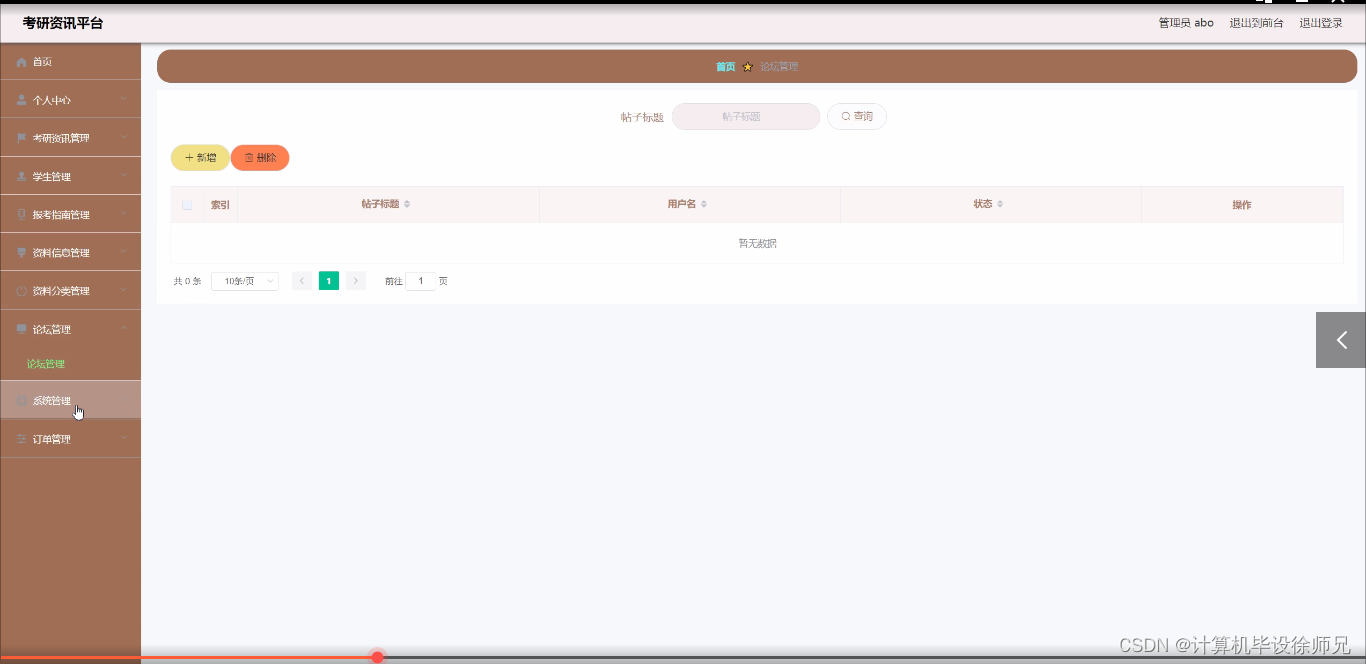
1 简介 大家好,我是程序员徐师兄,今天为大家带来的是Java基于SpringBootVue的考研资讯平台 Java基于SpringBoot的考研资讯平台,在系统当中学生可以根据不同的信息来实现该网站的考研资讯平台信息的管理。 系统主要分为前台和后台。主要包括…...

信钰证券:9月以来A股20家银行 获机构不同批次调研
Wind数据显现,自9月份以来,已经有20家银行获安排不同批次调研。其间常熟银行、瑞丰银行被调研次数较多,别离为20次、11次;宁波银行、渝农商行获安排调研家数居前,别离为206家、128家。从上市银行宣布的调研情况来看&am…...

应用商店优化的好处有哪些?
应用程序优化优势包括应用在商店的可见性和曝光度,高质量和被相关用户的更好发现,增加的应用下载量,降低用户获取成本和持续增长,增加应用收入和转化率以及全球受众范围。 1、提高知名度并在应用商店中脱颖而出。 如果用户找不到…...
MacOS Pro笔记本硬盘升级纪实
背景 MacPro 2015 mid的苹果本,忽然心血来潮想升级一下SSD。三个步骤:做启动盘,时间机器备份,插新的SSD盘恢复。 过程 下载MacOS,macOS Monterey 12.7官方原版镜像: https://swcdn.apple.com/content/do…...

景联文科技:3D点云标注应用场景和专业平台
3D点云技术之所以得到广泛发展和应用,主要是因为它能够以一种直观、真实和全面的方式来表示和获取现实世界中的三维信息。 3D点云的优势: 真实感和立体感:3D点云数据能够呈现物体的真实感和立体感,使观察者能够更直观地理解物体的…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

NFT模式:数字资产确权与链游经济系统构建
NFT模式:数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新:构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议:基于LayerZero协议实现以太坊、Solana等公链资产互通,通过零知…...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...
Reasoning over Uncertain Text by Generative Large Language Models
https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829 1. 概述 文本中的不确定性在许多语境中传达,从日常对话到特定领域的文档(例如医学文档)(Heritage 2013;Landmark、Gulbrandsen 和 Svenevei…...

R语言速释制剂QBD解决方案之三
本文是《Quality by Design for ANDAs: An Example for Immediate-Release Dosage Forms》第一个处方的R语言解决方案。 第一个处方研究评估原料药粒径分布、MCC/Lactose比例、崩解剂用量对制剂CQAs的影响。 第二处方研究用于理解颗粒外加硬脂酸镁和滑石粉对片剂质量和可生产…...
