2023 泰山杯 --- Crypto wp
文章目录
- 题目
- 解题过程
- part1
- part2
- part3
- 解题代码
题目
from fastecdsa.curve import P521 as Curve
from fastecdsa.point import Point
from os import urandom
from random import getrandbits
import uuid
from Crypto.PublicKey import DSA
from Crypto.Util.number import *
import random
from hashlib import sha256flag = f"flag{{{uuid.uuid4()}}}".encode('utf-8')
m1 = b'****************'
m2 = b'****************'def gen(G):urand = bytes_to_long(urandom(256 // 8))while True:s = getrandbits(256) ^ urandQ = s * Gif isPrime(Q.x) and isPrime(Q.y):return Q.x, Q.ydef sign(m, k, x, p, q, g):cm = sha256(m).digest()hm = bytes_to_long(cm)r = pow(g, k, p) % qs = (hm + x * r) * inverse(k, q) % qreturn r, sdef encrypt(msg):p, q, r, t = getPrime(256), getPrime(256), getPrime(256), getPrime(256)pubkey = p ** 2 * q * r * tn = pubkeyphi = (p - 1) * (q - 1) * (r - 1) * (t - 1)privkey = inverse(n, phi)c = long_to_bytes(pow(bytes_to_long(msg), pubkey, pubkey))return [c, pubkey, privkey]def verify(message, r, s, p, q, g, y): cm = sha256(message).digest()hm = bytes_to_long(cm)w = pow(s, q - 2, q) u1 = (hm * w) % q u2 = (r * w) % q v = ((pow(g, u1, p) * pow(y, u2, p)) % p) % q return v == r ecc_p = Curve.p
a = Curve.a
b = Curve.b
Gx = Curve.gx
Gy = Curve.gy
G = Point(Gx, Gy, curve=Curve)
p, q = gen(G)
n = p * q
print(f"a={a}")
print(f"b={b}")
print(f"ecc_p={ecc_p}")
print(f"n={n}")
x = bytes_to_long(flag)
cm1 = encrypt(m1)
cm2 = encrypt(m2)
key = DSA.generate(int(2048))
g = key.g
assert q > x
k = random.randint(1, q - 1)
r1, s1 = sign(m1, k, x, p, q, g)
r2, s2 = sign(m2, k, x, p, q, g)
print(f"cm1={cm1}")
print(f"cm2={cm2}")
print(f's1 = {s1}')
print(f'r1 = {r1}')
print(f'r2 = {r2}')
print(f's2 = {s2}')"""
a=-3
b=1093849038073734274511112390766805569936207598951683748994586394495953116150735016013708737573759623248592132296706313309438452531591012912142327488478985984
ecc_p=6864797660130609714981900799081393217269435300143305409394463459185543183397656052122559640661454554977296311391480858037121987999716643812574028291115057151
n=17892143742135558659464483241031582705399015704984635198259117502698806062144577358841580186430592021484784182374984891504991723987372158404717308894627025254370106060682124762121644746055038786733570766842371672272269500805787962472846195694411232153017387865489974233181909133999038179766349022983643293490318883cm1=[b'~(\x13K\xbd\x07\xf6\xac\x0f^\xff\xc0\x11\xf4\\-[bd\xd4\xee\xad\xd3\x12hY\xa9\xfawU6\tM\xd8\xc7$Q\x08fe\x0e\xa6V\x84Af\xc2\x90\xff\x0b\xb3\xf7\t\xeb\x1f\x92\xe9_\xc2d\x0b,\xb8j\xa7x\xb7\xd8.\x01\x0f\xb3\xfb\x84}\x18M_$J\x19WS\x19\xe4\xac|\xfb\xab\\\xddE\xe8K\x11\x85\x94I\x88\x06\xda\xd9\xa5\xd3%\xdeZ\xc0\xa1\x96K\x8f\xc9\xd6rZ\xf9\x80\x03\xb6\xe7&\xc7\xba\xfa\x11\x0e\x17\x03\xc6@\xf9\xe1\x91\xc3\x98\xfd~\xb4,\xbf+\xf1\x9c\x13\xf9\xcb\xd3\xa2\xcd\t\xc1\xa0\x16\xac(kO\x0e', 4210112960230753389177723103991057503675404064215473253619064996297654205031972289490914887593241466687180915490587736105591295790203391680056466722777574962131018329890483040708509359428184782432390334491747709835762154148954222667111743029165387940794322517656416298463983972364481679736217231237972603248180412651171720538869199141557228108454144762163387122885891997412124486368093, 34467673940229375549861096366968383350573853982091018691379038369575391106133342982206096859322434387821396329105522038690695490560975568642248771969263414977884644851551873207137010180591879084640509485920597821696620795026052163156567900184188166776652129980691756851240082925443033375548789315858902528245]cm2=[b"\x04L\xfbgl\x83\x8c\xd0\xd1\x94\xaeH\x15\x1f\x9d\r\xfe4Qo\x1f\x0e\xac\x99\x10\xd7p\x05\x0e\xe1Z\xde\xf1-\x90'\xfd\n\xcb\x11\x95\xe7\xfd\xb4\xa9\xe1g\xba\x88\x97h\t\x114\x8f\r\xa4\xf38\xf59\xbdbt\x8f\\U\xeau\x0e\xe2C\xd0\xbf\xb0\x0b\xe4\xfb\\\xb1\xe6\xd8\xc9K\x99F\n\xd1s(\xda \xe1\xa0)st\xdduv\x05\t\x97\x85\xbfdnr$\xeee<\xdd\xa2j\xd1l\x0c\x14\xe0\x9d!\x9d\x85J\xe6\x08\xf3\x8b\xf5^\xb6\xf9\xd5\xf8\xf1\xa9\x05\x11\xf2\x1f\xe6L}_?\xdc\xf1\xcf_\x19K\x9d?F\x11\x8a\xd6m_", 2107035726522358468787800437216735702294054489210423482763141344245971658038208946943384473505445944203654154393368969472650747972993446483863354738530464536671191192852772663305104685295729636566877550779644763943501495227449049599621704191810033993441720482366622086425653151565702373624357844645714794047547901924425604430887869417863146263310137069165358904526698570368614646908659, 25851316624668868073282577242443094459803237792257031370809123539176662555947554778083633535689341409219664781371076460089226128423940382827297717468898042144540839805840728213520942720971834042050337266075935231655467146339599134132537675265039256700087188339078240329238442682883808814292004154090735239739]s1 = 1147444956942488206425397540690496331513776719096397579521439800869593847794208912124600845863795170543614454413750492051491732502087262731130173253134510721
r1 = 1157925007400122568661548726339484089282532284376929635262438142895805835643192575599802310792451479232905705228133875039893052991121145062272055314297648646
r2 = 1157925007400122568661548726339484089282532284376929635262438142895805835643192575599802310792451479232905705228133875039893052991121145062272055314297648646
s2 = 1705053872995228285447305031429522382982990819347651751236442503354782702527682212062279231285695576661552718820729949632674150767988313498856519278708115047"""解题过程
part1
y 2 = x 3 + a ∗ x + b y^2 = x^3+a*x+b y2=x3+a∗x+b
两边同时乘上 x 2 x^2 x2
⇒ x 2 y 2 = x 5 + a ∗ x 3 + b ∗ x 2 \Rightarrow x^2y^2 = x^5+a*x^3+b*x^2 ⇒x2y2=x5+a∗x3+b∗x2
⇒ n 2 = x 5 + a ∗ x 3 + b ∗ x 2 \Rightarrow n^2 = x^5+a*x^3+b*x^2 ⇒n2=x5+a∗x3+b∗x2
此时构建一个在模Ep下的方程即可解出 x x x,也就是p,进而q = n//p
part2
本质上是dp泄露,其中
n = p 2 ∗ q ∗ r ∗ t n = p^2*q*r*t n=p2∗q∗r∗t
p h i = p ∗ ( p − 1 ) ( q − 1 ) ∗ ( r − 1 ) ∗ ( t − 1 ) phi = p*(p-1)(q-1)*(r-1)*(t-1) phi=p∗(p−1)(q−1)∗(r−1)∗(t−1)
p h i 1 = ( p − 1 ) ( q − 1 ) ( r − 1 ) ( t − 1 ) phi_1 = (p-1)(q-1)(r-1)(t-1) phi1=(p−1)(q−1)(r−1)(t−1)
e = n e = n e=n
e d 1 ≡ 1 m o d p h i 1 ed_1 \equiv 1 \space mod \space phi_1 ed1≡1 mod phi1
m e d 1 m o d n ≡ m 1 + k ∗ p h i 1 m o d p ∗ q ∗ r ∗ t m^{ed_1} \space mod \space n\equiv m^{1+k*phi_1} \space mod \space p*q*r*t med1 mod n≡m1+k∗phi1 mod p∗q∗r∗t
根据费马小定理
a p − 1 ≡ 1 m o d p a^{p-1} \equiv 1 \space mod \space p ap−1≡1 mod p
⇒ m 1 + k ∗ p h i 1 m o d p ∗ q ∗ r ∗ t ≡ m m o d p ∗ q ∗ r ∗ t \Rightarrow m^{1+k*phi_1} \space mod \space p*q*r*t \equiv m \space mod \space p*q*r*t ⇒m1+k∗phi1 mod p∗q∗r∗t≡m mod p∗q∗r∗t
⇒ m e d 1 m o d n − m ≡ 0 m o d p ∗ q ∗ r ∗ t \Rightarrow m^{ed_1} \space mod \space n - m \equiv 0 \space mod \space p*q*r*t ⇒med1 mod n−m≡0 mod p∗q∗r∗t
又 ∵ n = p 2 ∗ q ∗ r ∗ t 又\because n = p^2*q*r*t 又∵n=p2∗q∗r∗t
则有, m e d 1 m o d n − m 与 n 存在最大公约数 p ∗ q ∗ r ∗ t 则有,m^{ed_1} \space mod \space n - m与n存在最大公约数p*q*r*t 则有,med1 mod n−m与n存在最大公约数p∗q∗r∗t
所以,存在任意自然数 m ,使得 p ∗ q ∗ r ∗ t = g c d ( m e d 1 m o d n − m , n ) , m ∈ [ 2 , p ∗ q ∗ r ∗ t ) 所以,存在任意自然数m,使得p*q*r*t = gcd(m^{ed_1} \space mod \space n - m,n),m\in [2,p*q*r*t) 所以,存在任意自然数m,使得p∗q∗r∗t=gcd(med1 mod n−m,n),m∈[2,p∗q∗r∗t)
⇒ p ∗ q ∗ r ∗ t = g c d ( m e d 1 m o d n − m , n ) \Rightarrow p*q*r*t = gcd(m^{ed_1} \space mod \space n - m,n) ⇒p∗q∗r∗t=gcd(med1 mod n−m,n)
然后分别解出 m 1 m_1 m1和 m 2 m_2 m2即可
part3
这部分采用了同一个随机密钥k签名了两次,又已知 m 1 m_1 m1和 m 2 m_2 m2,则有
s 1 ≡ ( H ( m 1 ) + x r ) k − 1 m o d q s_1 \equiv (H(m_1)+xr)k^{-1} \space mod \space q s1≡(H(m1)+xr)k−1 mod q
s 2 ≡ ( H ( m 2 ) + x r ) k − 1 m o d q s_2 \equiv (H(m_2)+xr)k^{-1} \space mod \space q s2≡(H(m2)+xr)k−1 mod q
变换一下,两边同时乘以k
s 1 k ≡ H ( m 1 ) + x r m o d q s_1k \equiv H(m_1)+xr \space mod \space q s1k≡H(m1)+xr mod q
s 2 k ≡ H ( m 2 ) + x r m o d q s_2k \equiv H(m_2)+xr \space mod \space q s2k≡H(m2)+xr mod q
两式两相减,消去 x r xr xr
( s 1 − s 2 ) k ≡ H ( m 1 ) − H ( m 2 ) m o d q (s_1-s_2)k \equiv H(m_1)-H(m_2) \space mod \space q (s1−s2)k≡H(m1)−H(m2) mod q
⇒ k ≡ ( s 1 − s 2 ) − 1 ( H ( m 1 ) − H ( m 2 ) ) m o d q \Rightarrow k \equiv (s_1-s_2)^{-1}(H(m_1)-H(m_2)) \space mod \space q ⇒k≡(s1−s2)−1(H(m1)−H(m2)) mod q
当我们知道随机密钥k,q,hm,r,s时候,并且那么我们就可以根据签名算法
s = ( H ( m ) + x r ) k − 1 m o d q s = (H(m)+xr)k^{-1} \space mod \space q s=(H(m)+xr)k−1 mod q
计算私钥出 x x x,即flag
x ≡ r − 1 ( k s − H ( m ) ) m o d q x \equiv r^{-1}(ks-H(m)) \space mod \space q x≡r−1(ks−H(m)) mod q
解题代码
#sage
from hashlib import sha256
from Crypto.Util.number import *
import gmpy2a = -3
b = 1093849038073734274511112390766805569936207598951683748994586394495953116150735016013708737573759623248592132296706313309438452531591012912142327488478985984
ecc_p = 6864797660130609714981900799081393217269435300143305409394463459185543183397656052122559640661454554977296311391480858037121987999716643812574028291115057151
n = 17892143742135558659464483241031582705399015704984635198259117502698806062144577358841580186430592021484784182374984891504991723987372158404717308894627025254370106060682124762121644746055038786733570766842371672272269500805787962472846195694411232153017387865489974233181909133999038179766349022983643293490318883
s1 = 1147444956942488206425397540690496331513776719096397579521439800869593847794208912124600845863795170543614454413750492051491732502087262731130173253134510721
r1 = 1157925007400122568661548726339484089282532284376929635262438142895805835643192575599802310792451479232905705228133875039893052991121145062272055314297648646
s2 = 1705053872995228285447305031429522382982990819347651751236442503354782702527682212062279231285695576661552718820729949632674150767988313498856519278708115047cm1=[b'~(\x13K\xbd\x07\xf6\xac\x0f^\xff\xc0\x11\xf4\\-[bd\xd4\xee\xad\xd3\x12hY\xa9\xfawU6\tM\xd8\xc7$Q\x08fe\x0e\xa6V\x84Af\xc2\x90\xff\x0b\xb3\xf7\t\xeb\x1f\x92\xe9_\xc2d\x0b,\xb8j\xa7x\xb7\xd8.\x01\x0f\xb3\xfb\x84}\x18M_$J\x19WS\x19\xe4\xac|\xfb\xab\\\xddE\xe8K\x11\x85\x94I\x88\x06\xda\xd9\xa5\xd3%\xdeZ\xc0\xa1\x96K\x8f\xc9\xd6rZ\xf9\x80\x03\xb6\xe7&\xc7\xba\xfa\x11\x0e\x17\x03\xc6@\xf9\xe1\x91\xc3\x98\xfd~\xb4,\xbf+\xf1\x9c\x13\xf9\xcb\xd3\xa2\xcd\t\xc1\xa0\x16\xac(kO\x0e', 4210112960230753389177723103991057503675404064215473253619064996297654205031972289490914887593241466687180915490587736105591295790203391680056466722777574962131018329890483040708509359428184782432390334491747709835762154148954222667111743029165387940794322517656416298463983972364481679736217231237972603248180412651171720538869199141557228108454144762163387122885891997412124486368093, 34467673940229375549861096366968383350573853982091018691379038369575391106133342982206096859322434387821396329105522038690695490560975568642248771969263414977884644851551873207137010180591879084640509485920597821696620795026052163156567900184188166776652129980691756851240082925443033375548789315858902528245]
cm2=[b"\x04L\xfbgl\x83\x8c\xd0\xd1\x94\xaeH\x15\x1f\x9d\r\xfe4Qo\x1f\x0e\xac\x99\x10\xd7p\x05\x0e\xe1Z\xde\xf1-\x90'\xfd\n\xcb\x11\x95\xe7\xfd\xb4\xa9\xe1g\xba\x88\x97h\t\x114\x8f\r\xa4\xf38\xf59\xbdbt\x8f\\U\xeau\x0e\xe2C\xd0\xbf\xb0\x0b\xe4\xfb\\\xb1\xe6\xd8\xc9K\x99F\n\xd1s(\xda \xe1\xa0)st\xdduv\x05\t\x97\x85\xbfdnr$\xeee<\xdd\xa2j\xd1l\x0c\x14\xe0\x9d!\x9d\x85J\xe6\x08\xf3\x8b\xf5^\xb6\xf9\xd5\xf8\xf1\xa9\x05\x11\xf2\x1f\xe6L}_?\xdc\xf1\xcf_\x19K\x9d?F\x11\x8a\xd6m_", 2107035726522358468787800437216735702294054489210423482763141344245971658038208946943384473505445944203654154393368969472650747972993446483863354738530464536671191192852772663305104685295729636566877550779644763943501495227449049599621704191810033993441720482366622086425653151565702373624357844645714794047547901924425604430887869417863146263310137069165358904526698570368614646908659, 25851316624668868073282577242443094459803237792257031370809123539176662555947554778083633535689341409219664781371076460089226128423940382827297717468898042144540839805840728213520942720971834042050337266075935231655467146339599134132537675265039256700087188339078240329238442682883808814292004154090735239739]
#solve ecc to get q
R.<x> = PolynomialRing(Zmod(ecc_p))
f = x^5+a*x^3+b*x^2-n^2
result = f.roots()
p = int(result[0][0])
q = n//p
#solve rsa to get m1 and m2
c1, pubkey1, privkey1 = cm1
p1 = gmpy2.gcd(int(pow(5,privkey1*pubkey1,pubkey1)-5),int(pubkey1))
m1 = long_to_bytes(int(pow(bytes_to_long(c1),privkey1,p1)))c2, pubkey2, privkey2 = cm2
p2 = gmpy2.gcd(int(pow(5,privkey2*pubkey2,pubkey2)-5),int(pubkey2))
m2 = long_to_bytes(int(pow(bytes_to_long(c2),privkey2,p2)))#solve dsa
hm1 = bytes_to_long(sha256(m1).digest())
hm2 = bytes_to_long(sha256(m2).digest())
k = gmpy2.invert((s1 - s2), q) * (hm1 - hm2) % q
x = (s1 * k - hm1) * gmpy2.invert(r1, q) % q
flag = long_to_bytes(x)
print(flag)
#flag{d55a50f1-c95b-4e56-a7f7-b0efa1dc1d04}
【看似鸡毛蒜皮的琐碎小事,最消磨孝心善心。】
相关文章:

2023 泰山杯 --- Crypto wp
文章目录 题目解题过程part1part2part3 解题代码 题目 from fastecdsa.curve import P521 as Curve from fastecdsa.point import Point from os import urandom from random import getrandbits import uuid from Crypto.PublicKey import DSA from Crypto.Util.number impor…...

蓝桥杯每日一题20233.10.10
题目描述 回文日期 - 蓝桥云课 (lanqiao.cn) 题目分析 对于此题,我们最先想到的是暴力解法,将每一种情况经行循环查找,在查找的过程中记录下答案,回文日期就是字符串判断回文,ABABBABA型回文日期可以将回文经行特判…...

366. 寻找⼆叉树的叶⼦节点
366. 寻找⼆叉树的叶⼦节点 这道题混用二叉树递归 「遍历」和「分解问题」 两种思维模式。 class FindLeaves:"""366. 寻找⼆叉树的叶⼦节点https://leetcode.cn/problems/find-leaves-of-binary-tree/"""def solution(self, root):self.res …...
python - excel 设置样式
文章目录 前言python - excel 设置样式1. 准备2. 示例2.1. 给单元格设置样式"等线"、大小为24磅、斜体、红色颜色和粗体2.2. 给第二行设置样式"宋体"、大小为16磅、斜体、红色颜色和粗体2.3. 给第三行数据设置垂直居中和水平居中2.4. 给第四行设置行高为30…...
)
Gemmini测试test文件chisel源码详解(一)
DMACommandTrackerTest.scala 源码如下: package gemminiimport scala.collection.mutable.ArrayBufferimport chisel3._ import chisel3.iotesters.{ChiselFlatSpec, PeekPokeTester}class DMACommandTrackerTester(c: DMAReadCommandTracker[UInt]) extends Pee…...

RabbitMQ中的手动应答和自动应答
当使用RabbitMQ来处理消息时,消息确认是一个重要的概念。RabbitMQ提供了两种不同的消息确认方式:自动应答(Automatic Acknowledgment)和手动应答(Manual Acknowledgment)。这两种方式适用于不同的应用场景&…...
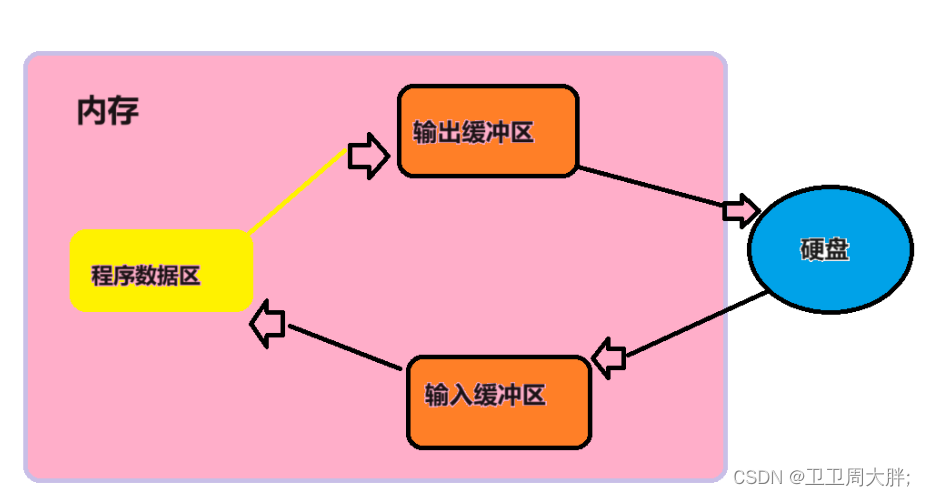
【C语言】文件的操作与文件函数的使用(详细讲解)
前言:我们在学习C语言的时候会发现在编写一个程序的时候,数据是存在内存当中的,而当我们退出这个程序的时候会发现这个数据不复存在了,因此我们可以通过文件把数据记录下来,使用文件我们可以将数据直接存放在电脑的硬盘…...

ROS-PX4仿真笔记_1
offbord模式测试 rosrun offboard_pkg position stablelize模式 lqr控制器实验 roslaunch px4 fast_test.launch 无人机起飞1.5-2m sh mybot_gazebo.sh#roslaunch px4 fast_racing.launch & sleep 20; roslaunch ego_planner single_run_in_gazebo.launch & sleep 1…...

使用 Python 中的小波变换信号驾驭股票价格的波动
一、简介 股票上涨和下跌,创造出像海浪一样难以预测的模式和走势。然而,就像科学家通过了解下面的水流来预测波浪的运动一样,我们也可以使用类似的工具破译股票市场的一些模式。 通过利用小波变换的力量,我们深入表面,试图揭示驱动股价的深层原因。这段旅程不仅仅涉及数字…...
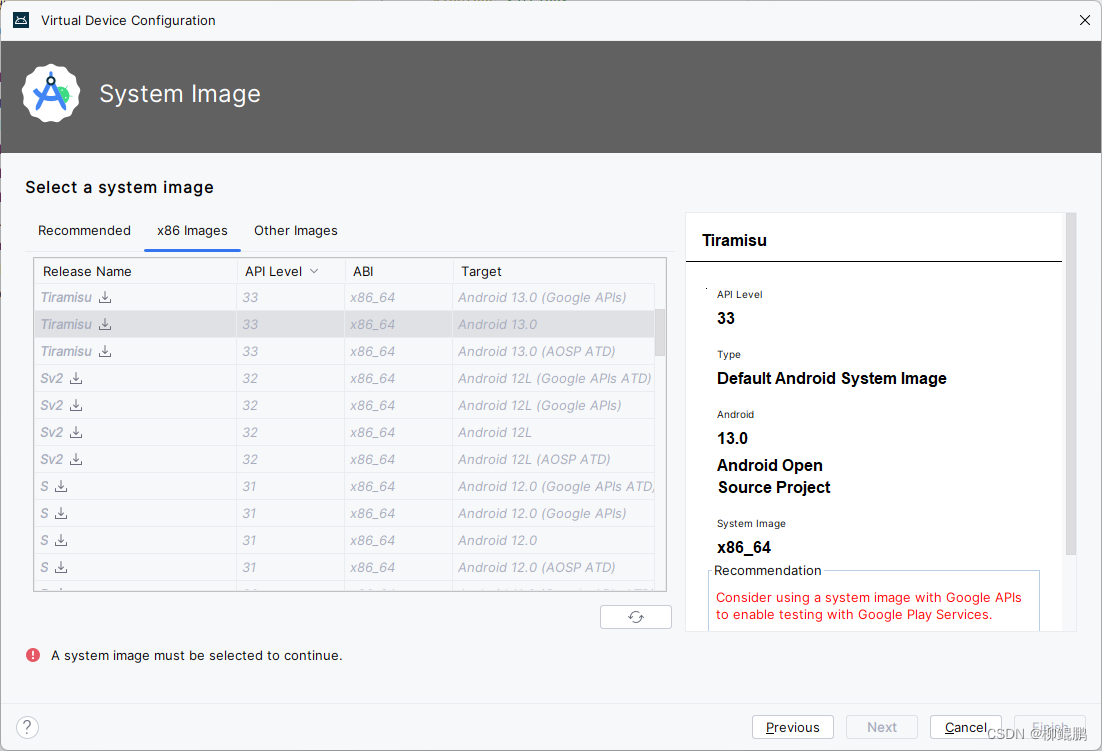
AndroidStudio模拟器,没有Google Play的就有ROOT权限
正确选择版本 测试 D:\>adb shell emulator64_x86_64:/ $ su emulator64_x86_64:/ #...

复选框 前端代码
表单中复选框选项 <el-form-item label="是否公开:" hidden="true"><input type="checkbox...

每日一练 | 网络工程师软考真题Day41
1、包过滤防火墙对通过防火墙的数据包进行检查,只有满足条件的数据包才能通过,对数据包的检查内容一般不包括 。 A.源地址 B.目的地址 C.协议 D.有效载荷 2、下面关于ARP木马的描述中,错误的…...

vue使用pinia存储数据并保持数据持久化
在Vue中使用Pinia存储数据并保持数据持久化,你可以遵循以下步骤: 安装Pinia:首先,你需要安装Pinia。可以通过npm或yarn来安装它。在终端中运行以下命令: npm install pinia# 或者使用yarn yarn add pinia创建Pinia St…...
k8s - Flannel
1.Flannel概念剖析 Flannel是 CoreOS 团队针对 Kubernetes 设计的一个覆盖网络(Overlay Network)工具,其目的在于帮助每一个使用 Kuberentes 的 CoreOS 主机拥有一个完整的子网。这次的分享内容将从Flannel的介绍、工作原理及安装和配置三方…...
服务器中了balckhoues勒索病毒怎么办?勒索病毒解密,数据恢复
近日,云天数据恢复中心发现,有多位用户的服务器中了一种名为balckhoues的勒索病毒,因为绝大多数用户是第一次遇到这种情况,所以对这种类型的勒索病毒并不是很了解。那接下来我们将对balckhoues勒索病毒做一个分析。 中毒特征 服务…...

react-pdf | Warning: TextLayer styles not found.
问题描述: 使用react-pdf展示pdf,但是报警告,Warning: TextLayer styles not found. 解决方法: <Pageloading{"加载中..."}renderAnnotationLayer{false}renderTextLayer{false}/> 添加属性如上,设…...

vue上传文件MD5加密
1.下载MD5依赖 npm install crypto-js 2.在utils文件夹中新增文件md5方法文件,文件名自定义(fileMd5Sum.js) import CryptoJs from crypto-js export default {// md5值计算fileMd5Sum(file) {let CryptoJS require("crypto-js"…...
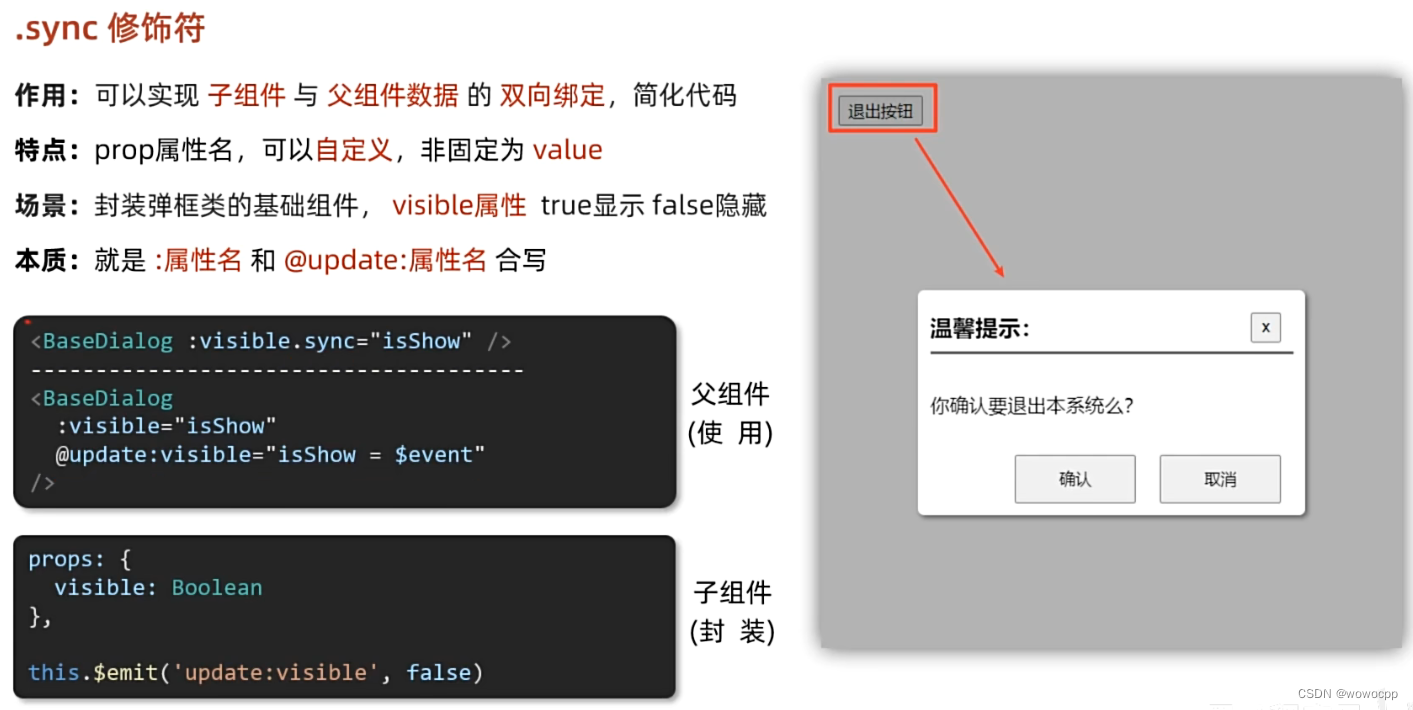
vue2 .sync 修饰符
vue2 .sync 修饰符 **创建 工程: H:\java_work\java_springboot\vue_study ctrl按住不放 右键 悬着 powershell H:\java_work\java_springboot\js_study\Vue2_3入门到实战-配套资料\01-随堂代码素材\day04\准备代码\13-sync修饰符 vue --version vue create v-sy…...

使用Tensorrt的一般步骤
使用Tensorrt的一般步骤 TensorRT的使用包括两个阶段:build and deployment。 build:该阶段主要完成模型转换(从caffe或TensorFlow到TensorRT),如下图所示,在模型转换时会完成前述优化过程中的层间融合&am…...
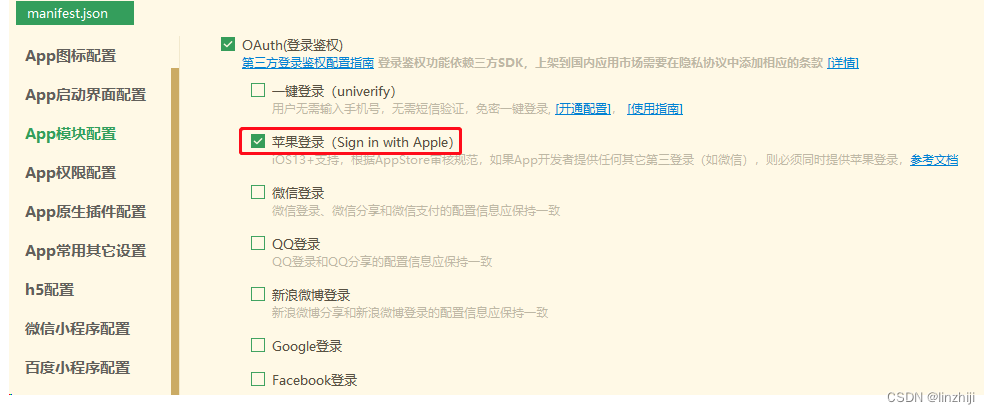
uniapp apple 苹果登录 离线本地打包
官方文档 uni-app官网 文档写的不全,没有写离线打包流程 加lib 签名里带 sign in with apple hbuilder开关 代码 测试代码,获取app里所有的provider uni.getProvider({service: oauth,success: function (res) {console.log(res.provider)uni.showT…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...

NFT模式:数字资产确权与链游经济系统构建
NFT模式:数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新:构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议:基于LayerZero协议实现以太坊、Solana等公链资产互通,通过零知…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...

服务器--宝塔命令
一、宝塔面板安装命令 ⚠️ 必须使用 root 用户 或 sudo 权限执行! sudo su - 1. CentOS 系统: yum install -y wget && wget -O install.sh http://download.bt.cn/install/install_6.0.sh && sh install.sh2. Ubuntu / Debian 系统…...
