【算法作业记录】
插入排序 递归实现
直接插入
#将a[n]插入有序区间a[0,n-1]中 时间复杂度 O(n)
def Insert(a,n):i=nwhile(i>0 and a[i-1]>a[i]):tmp=a[i]a[i]=a[i-1]a[i-1]=tmpi-=1return
#直接插入排序
def Insertsort(a,n):for i in range(1,n):#【1,n-1】if(a[i-1]>a[i]):Insert(a,i)return
#递归法实现直接插入:插入a[n]是建立在a[0,n-1]有序的基础之上
def RecursionInsertsort(a,n):if(n<=0):returnRecursionInsertsort(a,n-1)#递归实现【0,n-1】有序if(a[n-1]>a[n]):Insert(a,n)#再把a[n]插入有序数组a[0,n-1]中return
折半插入
#折半查找#在有序区[0,i-1]中二分查找元素a[i]应插入的位置 时间复杂度O(logN)
def BinInsert(a,i):low=0height=i-1insert=a[i]while(low<=height):mid=(low+height)//2if(insert<a[mid]):height=mid-1else: low=mid+1 j=i-1#height+1为要插入的位置,将【height+1,i-1】元素往后平移一步,空出a[height+1]的位置 while(j>=height+1):a[j+1]=a[j]j=j-1a[height+1]=insert #折半插入排序
def BinInsertSort(a,n):for i in range(1,n):if(a[i-1]>a[i]):BinInsert(a,i)print(str(i)+":"+str(a))
#递归实现折半插入
def RecursionBinInsertSort(a,n):if(n<=0):returnRecursionBinInsertSort(a,n-1)if(a[n-1]>a[n]):BinInsert(a,n)return list1 = [1,4,6,3,7,9,2,8,5,0]
print("排序前:"+str(list1))
#Insertsort(list1,len(list1))
#RecursionInsertsort(list1,len(list1)-1)
#BinInsertSort(list1,len(list1))
RecursionBinInsertSort(list1,len(list1)-1)
print("排序后:"+str(list1))
归并排序的算法改进
还有一个链表自底向上的未实现,参考笔记点我 点我
#107552304105 吕雅轩
#由于本人能力有限 除了网上给的四个优化策略想不出其它的了,以下是实现过程
#策略1: 若两数组直接拼起来就是有序的,就无需merge 即当arr[mid]<=arr[mid+1]
#策略2:小区间使用性能更高的插入排序
#策略3:全程使用1个和待排数组大小一样的临时数组作为辅助空间,避免了每一次merge都要new的浪费
#策略4:自顶向下需要递归调用log(n)的函数栈空间,可用自底向上的思路优化
#策略5:归并算法的空间复杂度是O(n),若想使空间复杂度优化为O(1),可以采用自底向上的链表法进行排序。
def merge_sort(a):#策略3:全局辅助空间global alal=list(range(len(a)))#_mergeSort(a,0,len(a)-1)#策略4:迭代法自底向上_mergeSortIterate(a)return#插入排序
def _insertSort(a,l,r):for i in range(l,r+1):#【1,n-1】if(a[i-1]>a[i]):j=iwhile(j>0 and a[j-1]>a[j]):tmp=a[j]a[j]=a[j-1]a[j-1]=tmpj-=1#用辅助空间把两个有序数组合并
def _merge_two_sorted_array(a,l,mid,r):for i in range(l,r+1):#[l,r]al[i]=a[i]i=l#左半有序数组的起始下标j=mid+1#右半有序数组的起始下标 #print(str(l)+":"+str(mid)+":"+str(r)+":"+str(a)) for k in range(l,r+1):#[l,r]if i==mid+1:a[k]=al[j]j+=1elif j>r:a[k]=al[i]i+=1elif al[i]<al[j]:a[k]=al[i]i+=1else:assert al[i]>=al[j]a[k]=al[j]j+=1 return
#递归实现归并排序
def _mergeSort(a,l,r):if l>=r:return#策略2:小区间使用性能更高的插入排序if (r-l)<=7:_insertSort(a,l,r)returnmid=l+(r-l)//2#防止(l+r)溢出_mergeSort(a,l,mid)_mergeSort(a,mid+1,r)#策略1:若有序左区间的最大元素小于有序右区间的最小元素,可直接合并if a[mid]<=a[mid+1]:return_merge_two_sorted_array(a,l,mid,r)return#策略4:迭代法自底向上
def _mergeSortIterate(a):n=len(a)size=1#每一次分段的长度i=0while(size<=n):i=0while(i+size<n):#确保后一段的存在,同时保证不越界_merge_two_sorted_array(a,i,i+size-1,min(i+size+size-1,n-1))i+=size+sizesize+=sizereturnlist1 = [10,9,8,7,6,4,5,3,2,1]
print("排序前:"+str(list1))
merge_sort(list1)
#_mergeSortIterate(list1)
print("排序后:"+str(list1))
相关文章:

【算法作业记录】
插入排序 递归实现 直接插入 #将a[n]插入有序区间a[0,n-1]中 时间复杂度 O(n) def Insert(a,n):inwhile(i>0 and a[i-1]>a[i]):tmpa[i]a[i]a[i-1]a[i-1]tmpi-1return #直接插入排序 def Insertsort(a,n):for i in range(1,n):#【1,n-…...

回归预测、分类预测、时间序列预测 都有什么区别?
回归预测、分类预测和时间序列预测都是统计和机器学习领域中的预测任务,它们在问题设置和解决的方式上有一些关键区别: 回归预测: 回归预测用于预测连续数值的输出,通常是实数。例如,预测房价、气温、销售额等连续型输…...

关于网络协议的若干问题(三)
1、当发送的报文出问题的时候,会发送一个 ICMP 的差错报文来报告错误,但是如果 ICMP 的差错报文也出问题了呢? 答:不会导致产生 ICMP 差错报文的有: ICMP 差错报文(ICMP 查询报文可能会产生 ICMP 差错报文…...
办公室人人在用的iTab桌面真的好用吗?
本人坐标北京,在一家中型互联网公司当社畜多年。最近发现一个奇怪的现象,我工位前后左右的同事都跟我在用一样的浏览器桌面——iTab新标签页。我表示莫非真的英雄所见略同? 我是去年1月份在刷B站时偶然刷到一条评论,有人分享自己…...

循环中的else语句
while 循环else结构: 循环可以和else配合使用,else下方缩进的代码指的是当循环正常结束之后要执行的代码. 需求:女朋友生气了,要惩罚:连续说5遍“老婆大人,我错了”,如果道歉正常完毕后女朋友就原谅我了:…...

三.镜头知识之FOV
三.镜头知识之视场角 最近试了很多sensor, 每次在选镜头时都对其提到的FOV参数一头雾水。不同的sensor要配不同的镜头,而不同的镜头由于焦距的不同,FOV也不一样。这其中有什么联系呢?FOV又分为HFOV(水平), VFOV( 垂直)…...
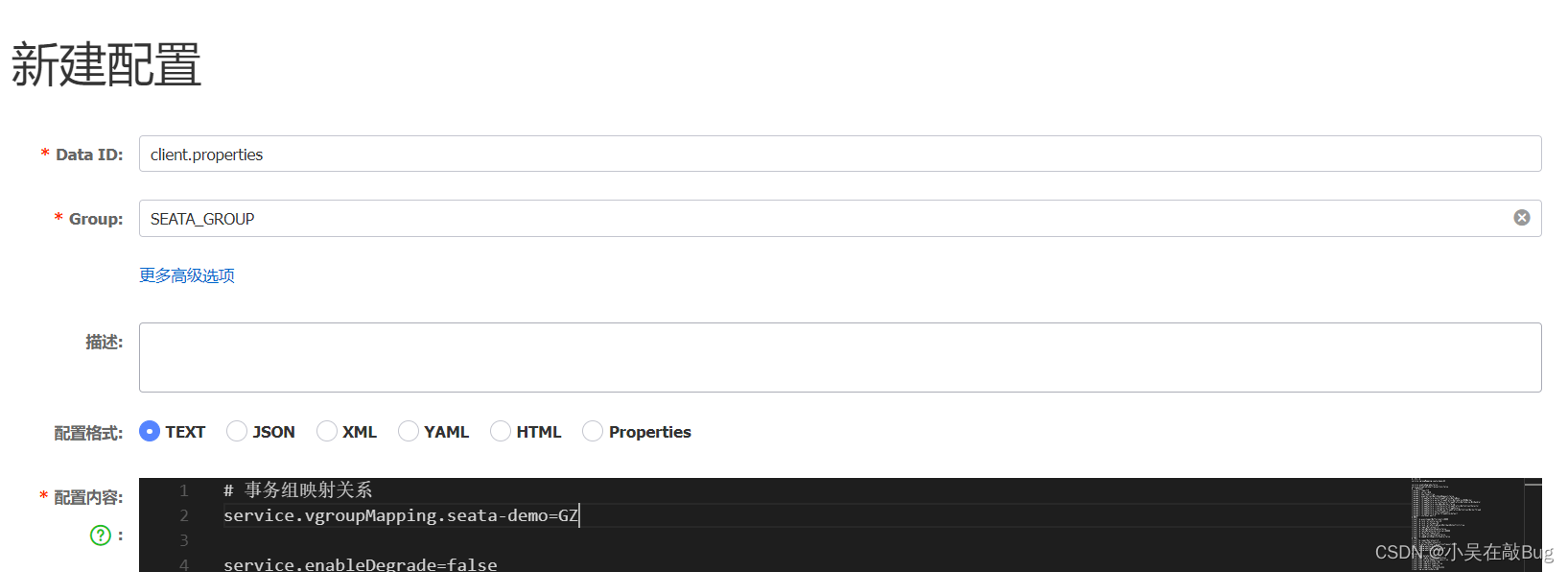
分布式事务入门
文章目录 分布式事务问题本地事务分布式事务演示分布式事务问题 理论基础CAP定理一致性可用性分区容错矛盾 BASE理论 SeataSeata的架构部署TC服务微服务集成seata 动手实践XA模式两阶段提交Seata的XA模型实现XA模式 AT模式Seata的AT模型流程梳理脏写问题实现AT模式 TCC模式流程…...

Ubuntu的中文乱码问题
一、Ubuntu的中文乱码问题 sudo apt-get install language-pack-zh-hans 二、修改/etc/environment(在文件的末尾追加): LANG"zh_CN.UTF-8" LANGUAGE"zh_CN:zh:en_US:en" 三、修改/var/lib/locales/supported.d/loca…...

[GXYCTF2019]Ping Ping Ping - RCE(空格、关键字绕过[3种方式])
[GXYCTF2019]Ping Ping Ping 1 解题流程1.1 小试牛刀1.2 三种解法1.2.1 解法一:变量定义拼接绕过1.2.2 解法二:base64编码绕过1.2.3 解法三:内联执行绕过2 思考总结1 解题流程 1.1 小试牛刀 1、提示?ip,结合题目名称,我们直接输入?ip=127.0.0.1 PING 127.0.0.1 (127.…...

ceph 分布式存储与部署
目录 一、存储基础: 1.单机存储设备: 2. 单机存储的问题: 3. 商业存储解决方案: 4. 分布式存储: 5. 分布式存储的类型: 二、Ceph 简介: 三、Ceph 优势: 四、Ceph 架构:…...

Go 结构体深度探索:从基础到应用
1. 结构体概述 在计算机编程中,数据结构是组织、管理和存储数据的一种方式,它允许高效地执行各种操作。Go语言中的结构体(Struct)是这些数据结构中的一员,它为数据的组织提供了一种具体的方式。 结构体可以被视为是多…...

分布式系统开发技术中的CAP定理原理
分布式系统开发技术中的CAP定理原理 在分布式系统开发中,CAP定理(一致性、可用性和分区容忍性)是指导我们设计、开发和维护系统的核心原理。该定理阐述了分布式系统中一致性、可用性和扩展性之间无法同时满足的矛盾关系,为我们提…...

Mysql 报错 You can‘t specify target table ‘表名‘ for update in FROM clause
翻译为:不能先select出同一表中的某些值,再update这个表(在同一语句中) 多半是update在where条件后又Select了一次,所以报错 SQL: UPDATE a SET a.name 1 WHERE a.id in (SELECT a.id FROM a WHERE ISNULL(a.id)) …...

【DevOps】DevOps—基本概念
文章目录 1. DevOps2. CI/CD 1. DevOps 维基百科定义: DevOps是一组过程、方法与系统的统称,用于促进 开发、技术运营 和 质量保障(QA) 部门之间的沟通、协作与整合。我理解DevOps是一种软件管理思维模式。 为什么会有DevOps呢&…...

发行版兴趣小组季度动态:Anolis OS 支持大热 AI 软件栈,引入社区合作安全修复流程
发行版兴趣小组(Special Interest Group) :旨在为龙蜥社区构建、发布和维护一个稳定的操作系统发行版。 秋天的季节,发行版兴趣小组在 AI、安全、国产 OS 领域同样也是硕果累累。一起来看一下第三季度发行版兴趣小组的成果总结有…...
android app开发环境搭建
Android是流行的移动设备原生应用开发平台,其支持Java语言以及Kotlin语言的开发环境,本文主要描述官方提供的Android studio集成开发环境搭建。 https://developer.android.google.cn/ 如上所示,从官方上下载最新版本的Android studio集成开…...

oracle入门笔记一
关系型数据库(Oracle) 一、市面上流行的关系型数据库 大型数据库:oracle(甲骨文)、DB2(IBM)、sysbase(sysbase) 百万以上数据 中型数据库:mysql…...
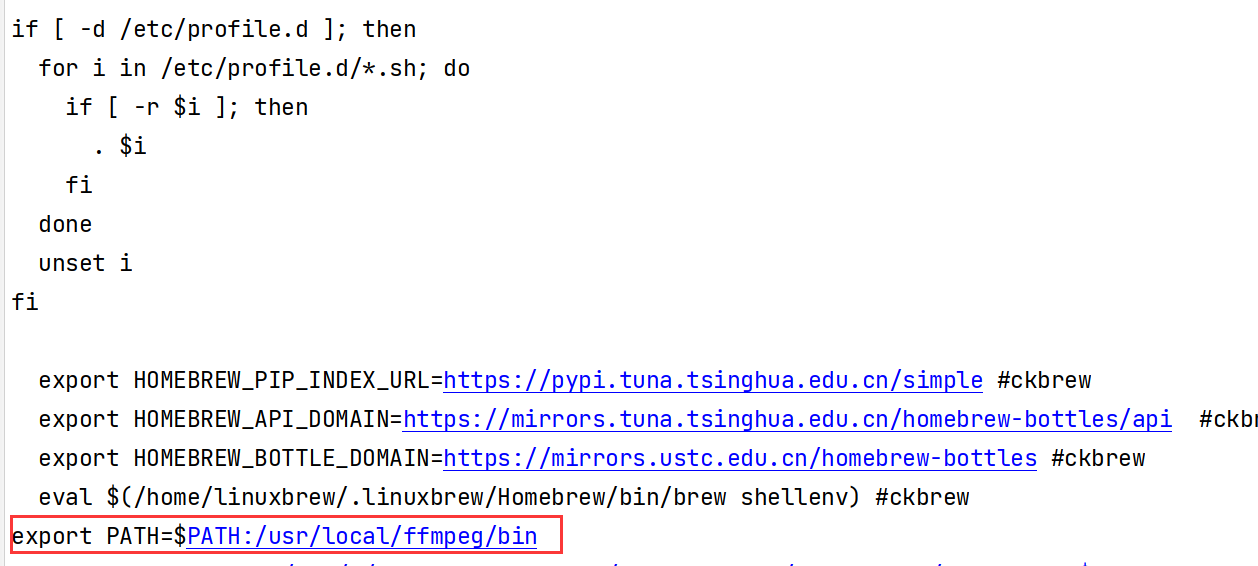
linux下安装ffmpeg的详细教程、ffmpeg is not installed
1、下载解压 wget http://www.ffmpeg.org/releases/ffmpeg-6.0.tar.gz tar -zxvf ffmpeg-6.0.tar.gz 2、 进入解压后目录,输入如下命令/usr/local/ffmpeg为自己指定的安装目录 cd ffmpeg-6.0 ./configure --prefix/usr/local/ffmpeg make sudo make install 3、配置变量 v…...
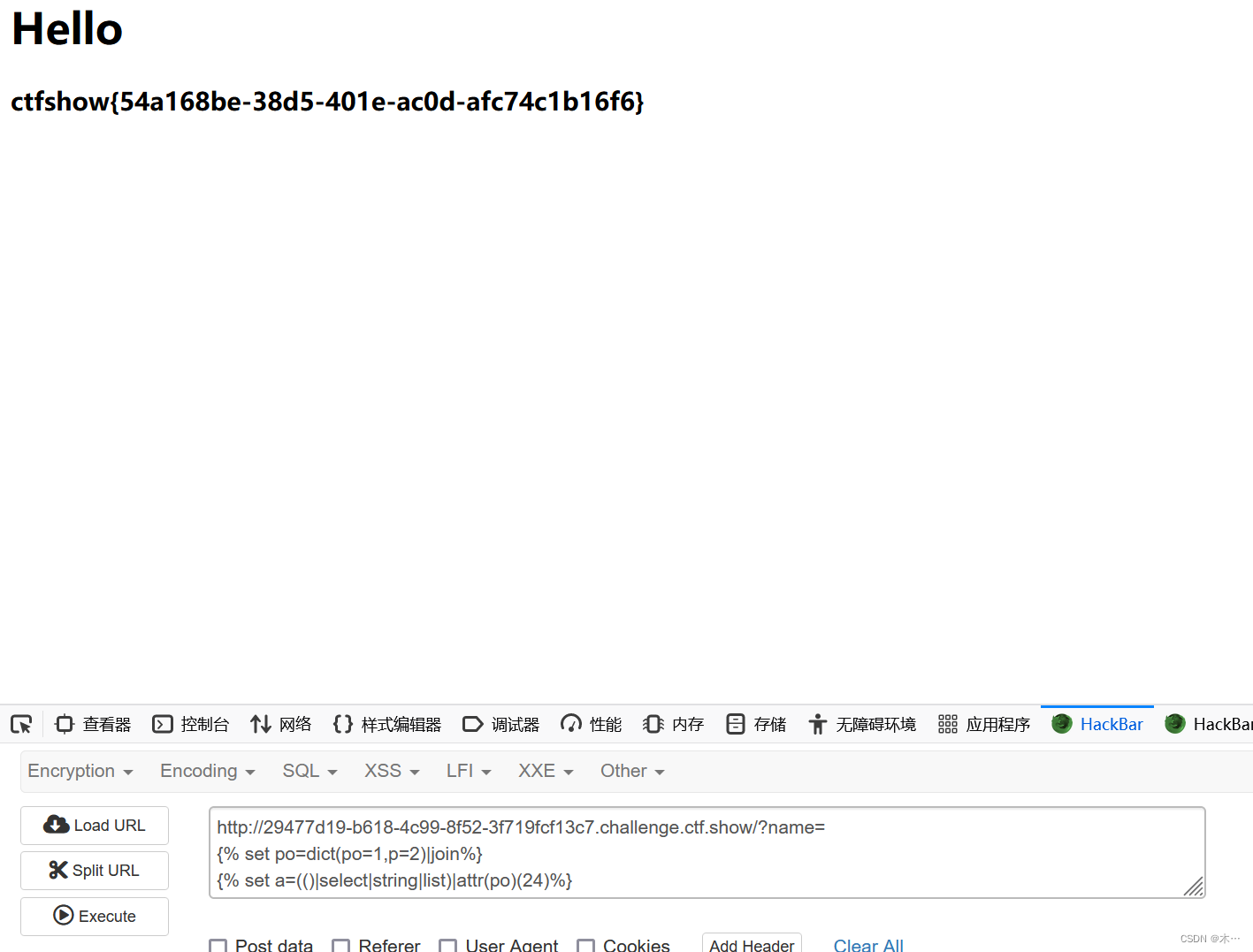
ctfshow-ssti
web361 名字就是考点,所以注入点就是name 先测试一下存不存在ssti漏洞 利用os模块,脚本 查看一下子类的集合 ?name{{.__class__.__base__.__subclasses__()}} 看看有没有os模块,查找os 利用这个类,用脚本跑他的位置 import …...

【ES6 03】变量解构赋值
变量解构赋值 数组解构赋值1 基操2 默认值 对象的解构赋值默认值注意 字符串的解构赋值数值与布尔值的解构赋值函数参数的解构赋值圆括号不得使用 作用 数组解构赋值 1 基操 ES6允许按照一定的模式从数组和对象中提取值从而对变量进行赋值,也即解构(De…...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...

Web 架构之 CDN 加速原理与落地实践
文章目录 一、思维导图二、正文内容(一)CDN 基础概念1. 定义2. 组成部分 (二)CDN 加速原理1. 请求路由2. 内容缓存3. 内容更新 (三)CDN 落地实践1. 选择 CDN 服务商2. 配置 CDN3. 集成到 Web 架构 …...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...

【C++特殊工具与技术】优化内存分配(一):C++中的内存分配
目录 一、C 内存的基本概念 1.1 内存的物理与逻辑结构 1.2 C 程序的内存区域划分 二、栈内存分配 2.1 栈内存的特点 2.2 栈内存分配示例 三、堆内存分配 3.1 new和delete操作符 4.2 内存泄漏与悬空指针问题 4.3 new和delete的重载 四、智能指针…...

Python+ZeroMQ实战:智能车辆状态监控与模拟模式自动切换
目录 关键点 技术实现1 技术实现2 摘要: 本文将介绍如何利用Python和ZeroMQ消息队列构建一个智能车辆状态监控系统。系统能够根据时间策略自动切换驾驶模式(自动驾驶、人工驾驶、远程驾驶、主动安全),并通过实时消息推送更新车…...

Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement
Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement 1. LAB环境2. L2公告策略2.1 部署Death Star2.2 访问服务2.3 部署L2公告策略2.4 服务宣告 3. 可视化 ARP 流量3.1 部署新服务3.2 准备可视化3.3 再次请求 4. 自动IPAM4.1 IPAM Pool4.2 …...

阿里云Ubuntu 22.04 64位搭建Flask流程(亲测)
cd /home 进入home盘 安装虚拟环境: 1、安装virtualenv pip install virtualenv 2.创建新的虚拟环境: virtualenv myenv 3、激活虚拟环境(激活环境可以在当前环境下安装包) source myenv/bin/activate 此时,终端…...

基于单片机的宠物屋智能系统设计与实现(论文+源码)
本设计基于单片机的宠物屋智能系统核心是实现对宠物生活环境及状态的智能管理。系统以单片机为中枢,连接红外测温传感器,可实时精准捕捉宠物体温变化,以便及时发现健康异常;水位检测传感器时刻监测饮用水余量,防止宠物…...

UE5 音效系统
一.音效管理 音乐一般都是WAV,创建一个背景音乐类SoudClass,一个音效类SoundClass。所有的音乐都分为这两个类。再创建一个总音乐类,将上述两个作为它的子类。 接着我们创建一个音乐混合类SoundMix,将上述三个类翻入其中,通过它管理每个音乐…...

32位寻址与64位寻址
32位寻址与64位寻址 32位寻址是什么? 32位寻址是指计算机的CPU、内存或总线系统使用32位二进制数来标识和访问内存中的存储单元(地址),其核心含义与能力如下: 1. 核心定义 地址位宽:CPU或内存控制器用32位…...
