EM算法 简明理解
E:Expection,期望步,利用估计的参数,来确定未知因变量的概率,并利用其来计算期望值。
M:Maximization,最大化,使用最大似然法更新参数值,使E步中期望值出现的概率最大。
例如网上较多的硬币例子,可以先估算硬币正反面参数A,但是无法获知隐变量B(无法知道某一次实验选择哪一枚硬币),因此可以分别计算每次试验选择了某一枚硬币的概率,也就是说计算了隐变量B的概率。明确了隐变量B的概率后,就可以依此概率,计算出一个期望值E。
通过更新参数A,使期望值为E的概率最大化,也就是M步中“最大化”的含义。
可以参考链接,https://zhuanlan.zhihu.com/p/78311644,这里面详细记录了硬币案例的EM迭代过程。
同样,将情况复杂化,例如现在有2位男生和2为女生,数据记录了他们的身高(但是不知道被记录着的性别),需要分别估计男女生身高分布的均值和方差,
这个时候有人就想到我们必须从某一点开始,并用迭代的办法去解决这个问题:我们先设定男生身高和女生身高分布的几个参数(初始值),然后根据这些参数去判断每一个样本(人)是男生还是女生,之后根据标注后的样本,计算出一个期望值,然后反过来重新估计参数,使期望值出现的概率最大化。之后再多次重复这个过程,直至稳定。这个算法也就是EM算法。
https://zhuanlan.zhihu.com/p/56377602
相关文章:

EM算法 简明理解
E:Expection,期望步,利用估计的参数,来确定未知因变量的概率,并利用其来计算期望值。 M:Maximization,最大化,使用最大似然法更新参数值,使E步中期望值出现的概率最大。…...
论坛项目小程序和h5登录
项目中安装uview出现npm安装uview 直接报错:创建一个package.json配置文件在进行安装。cmd到项目。初始化一个package.json文件(vue项目的配置文件) npm init --yes 安装uview项目点击关注进入管页面,需要验证用户是否登录查用户是…...

kubernetes集群pod中的pause容器作用
kubernetes集群pod中的pause容器作用 我们搭建完集群了以后,可以使用最简单的方式创建一个pod,随意你建立什么pod,去访问相应node上执行docker ps 就会看到有一种pause容器,但是你可能从来没有启用 etrics-scraper_dashboard-me…...
分配内存、MySQL事务、项目、动态规划)
【2.24】malloc()分配内存、MySQL事务、项目、动态规划
malloc是如何分配内存的? 在 Linux 操作系统中,虚拟地址空间的内部又被分为内核空间和用户空间两部分,不同位数的系统,地址空间的范围也不同。比如最常见的 32 位和 64 位系统,如下所示: 内核空间与用户空…...
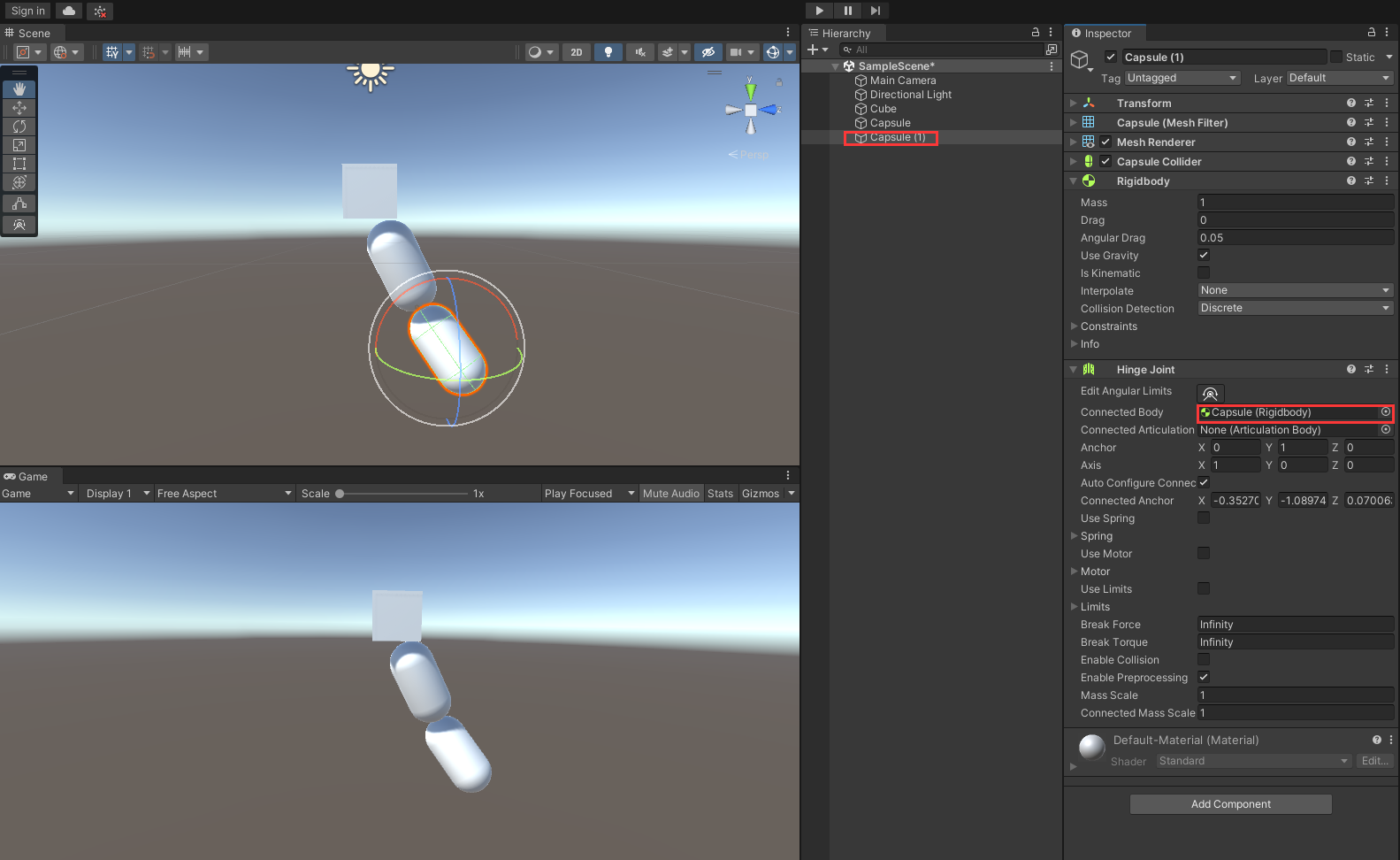
Unity——使用铰链关节制作悬挂物体效果
目的在场景中创建一个悬挂的物体,是把多个模型悬挂在一起可以自由摇摆,类似链条的效果效果图前言什么是铰链关节?铰链关节 将两个刚体(Rigid body)组会在一起,从而将其约束为如同通过铰链连接一样进行移动。…...
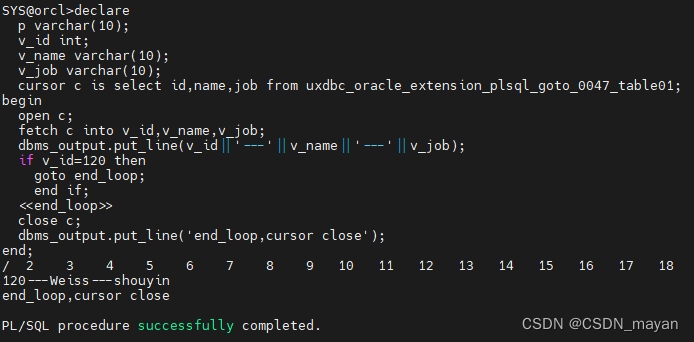
plsql过程语言之uxdb与oracle语法差异
序号场景uxdboracle1在存储过程中使用goto子句create or replace procedure uxdbc_oracle_extension_plsql_goto_0001_procedure01(t1 int) language plsql as $$ begin if t1%20 then goto even_number; else goto odd_number; end if; <<even_number>> raise…...

file_get_contents 打开本地文件报错: failed to open stream: No such file or directory
php 使用file_get_contents时报错 failed to open stream: No such file or directory (打开流失败,没有这样的文件或目录) 1. 首先确保文件路径没问题 最好是直接复制一下文件的路径 2. windows电脑可以右键该文件 → 属性→安全 →对象名称 选中后复制一下 3. 然后…...
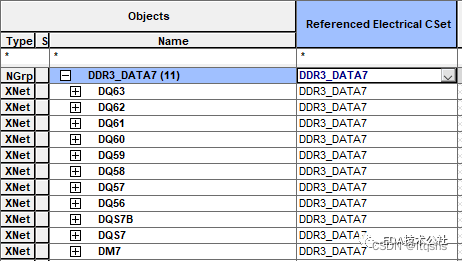
Candence allegro 创建等长的方法
随着源同步时序电路的发展,越来越多的并行总线开始采用这种时序控制电路,最典型的代表当属目前炙手可热的DDRx系列。下图这种点到点结构的同步信号,对于攻城狮来说,设置等长约束就非常easy了图片。 But,对于有4、6、8、、、等多颗DDR芯片的ACC同步信号来说,要设置等长约束…...

使用Python批量修改文件名称
下载了一些图片,想要更改其文件的名称。 试了许多方法,都不太理想。 于是想到了使用Python来实现。 需要用到的模块及函数: import osrename() 函数用于改变文件或文件夹的名称。它接受两个参数:原文件名和新文件名。 os.rena…...

【跟我一起读《视觉惯性SLAM理论与源码解析》】第八章 ORB-SLAM2中的特征匹配
特征匹配在ORB-SLAM2中是很重要的内容,函数有多次重载,一般而言分为以下 单目初始化下的特征匹配通过词袋进行特征匹配通过地图点投影进行特征匹配通过Sim(3)变化进行特征匹配 在单目初始化下的特征匹配是参考帧和当前帧之间的特…...

【Leedcode】数据结构中链表必备的面试题(第四期)
【Leedcode】数据结构中链表必备的面试题(第四期) 文章目录【Leedcode】数据结构中链表必备的面试题(第四期)1.题目2.思路图解(1)思路一(2)思路二3.源代码总结1.题目 相交链表: 如下(示例)&…...

【2023】助力Android金三银四面试
前言 新气象,新生机。在2023年的Android开发行业中,又有那些新的面试题出现呢?对于Android面试官的拷问,我们又如何正确去解答?万变不离其宗,其实只要Android的技术层面没变化,面试题也就是差不…...
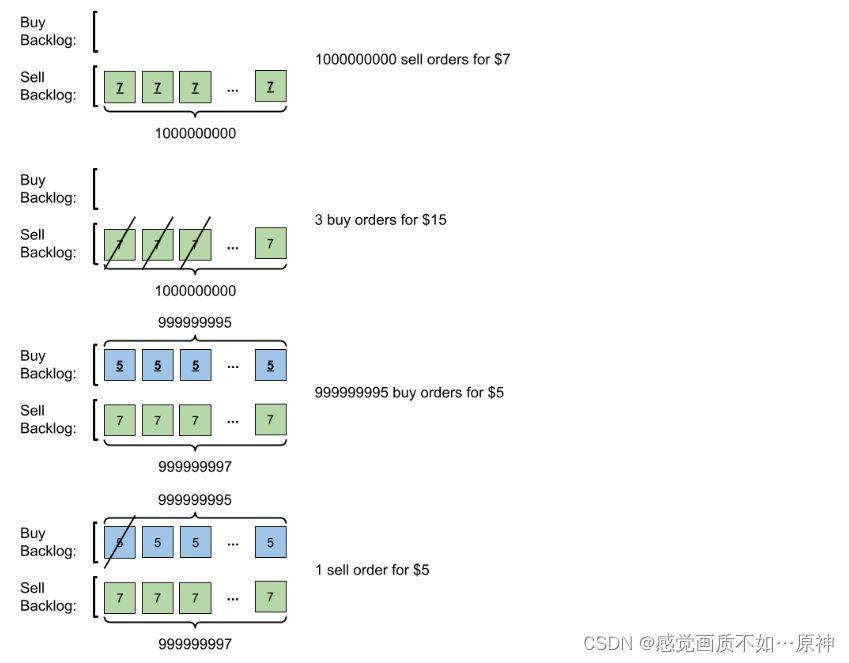
Leetcode.1801 积压订单中的订单总数
题目链接 Leetcode.1801 积压订单中的订单总数 Rating : 1711 题目描述 给你一个二维整数数组 orders,其中每个 orders[i] [pricei, amounti, orderTypei]表示有 amounti笔类型为 orderTypei、价格为 pricei的订单。 订单类型 orderTypei 可以分为两种…...

红帽Linux技术-cp命令
cp是一个复制文件或者目录的命令,其作用是将一个或多个文件或目录从源位置复制到目标位置。 格式:cp [选项] 源文件或目录 目标文件或目录 常用选项: -r:复制目录及其子目录下的所有文件和目录; -p:保留…...
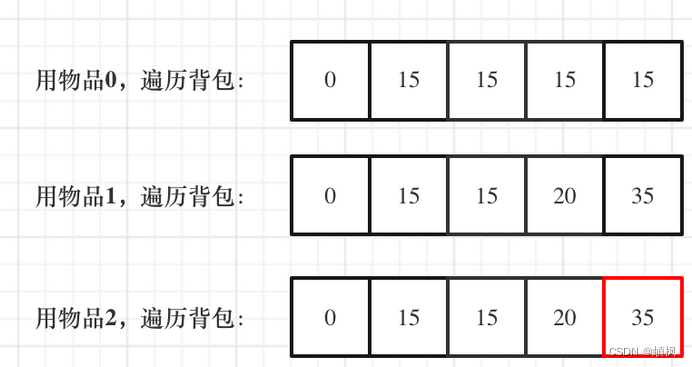
代码随想录算法训练营day41 | 动态规划 01背包问题基础 01背包问题之滚动数组
01背包问题基础 问题描述 有n件物品和一个最多能背重量为w 的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。每件物品只能用一次,求解将哪些物品装入背包里物品价值总和最大。 举个栗子 背包最大重量为4。 物品为: 重量价值…...
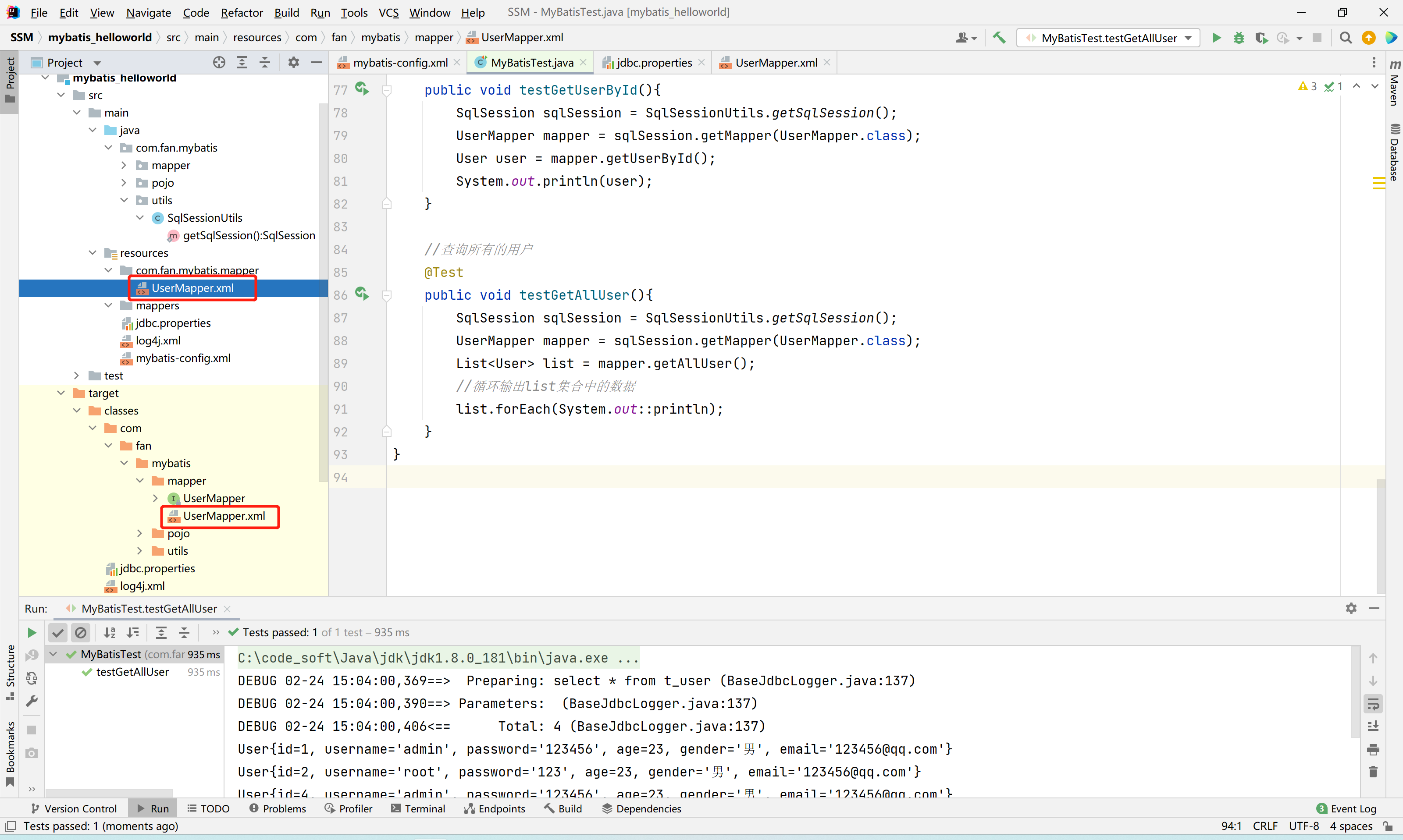
MyBatis学习笔记(三) —— MyBatis核心配置文件详解
3、核心配置文件详解 id是唯一标识,不能重复,但是在真正开发过程中,不可能一个项目中同时使用两个环境,肯定会使用其中的某一个,这时候它的default就比较重要了。 default是设置我们当前使用的默认环境的id <?x…...
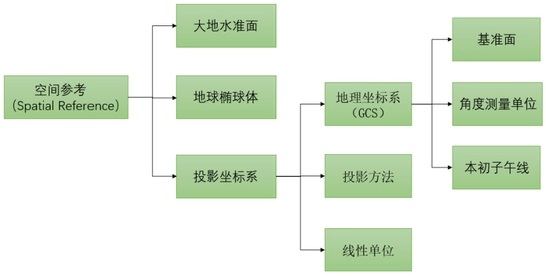
使用GDAL进行坐标转换
1、地理坐标系与投影坐标系空间参考中主要包含大地水准面、地球椭球体、投影坐标系等几部分内容。地图投影就是把地球表面的任意点,利用一定数学法则,转换到地图平面上的理论和方法,一般有两种坐标系来进行表示,分别是地理坐标系和…...

日常编程中和日期相关的代码和bug
本文主要是Java中和日期时间相隔的几个常用代码函数代码,做了总结,希望在日常编码中,可以帮到大家。 1.计算闰年 记住一个短语,“四年一润,百年不闰,四百再润”,不管换啥语言,相信…...

ATT与Intel汇编语法区别
寄存器、变量(常量)与立即数 在Intel汇编中,无论是寄存器、变量(常量)还是立即数,都是直接使用的,例如下列例子中分别加载一个变量(常量)与立即数到寄存器中:…...

Spring Cloud Alibaba全家桶(一)——Spring Cloud Alibaba介绍
前言 本文为 Spring Cloud Alibaba介绍 相关知识,下边将对微服务介绍(包括:系统架构演变、微服务架构介绍、常见微服务架构),Spring Cloud Alibaba介绍(包括:Spring Cloud Alibaba 的定位、Spri…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

反向工程与模型迁移:打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下,商品详情API作为连接电商平台与开发者、商家及用户的关键纽带,其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息(如名称、价格、库存等)的获取与展示,已难以满足市场对个性化、智能…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

Golang dig框架与GraphQL的完美结合
将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用,可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器,能够帮助开发者更好地管理复杂的依赖关系,而 GraphQL 则是一种用于 API 的查询语言,能够提…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

Spring数据访问模块设计
前面我们已经完成了IoC和web模块的设计,聪明的码友立马就知道了,该到数据访问模块了,要不就这俩玩个6啊,查库势在必行,至此,它来了。 一、核心设计理念 1、痛点在哪 应用离不开数据(数据库、No…...
 + 力扣解决)
LRU 缓存机制详解与实现(Java版) + 力扣解决
📌 LRU 缓存机制详解与实现(Java版) 一、📖 问题背景 在日常开发中,我们经常会使用 缓存(Cache) 来提升性能。但由于内存有限,缓存不可能无限增长,于是需要策略决定&am…...

PostgreSQL——环境搭建
一、Linux # 安装 PostgreSQL 15 仓库 sudo dnf install -y https://download.postgresql.org/pub/repos/yum/reporpms/EL-$(rpm -E %{rhel})-x86_64/pgdg-redhat-repo-latest.noarch.rpm# 安装之前先确认是否已经存在PostgreSQL rpm -qa | grep postgres# 如果存在࿰…...

解析奥地利 XARION激光超声检测系统:无膜光学麦克风 + 无耦合剂的技术协同优势及多元应用
在工业制造领域,无损检测(NDT)的精度与效率直接影响产品质量与生产安全。奥地利 XARION开发的激光超声精密检测系统,以非接触式光学麦克风技术为核心,打破传统检测瓶颈,为半导体、航空航天、汽车制造等行业提供了高灵敏…...

实战三:开发网页端界面完成黑白视频转为彩色视频
一、需求描述 设计一个简单的视频上色应用,用户可以通过网页界面上传黑白视频,系统会自动将其转换为彩色视频。整个过程对用户来说非常简单直观,不需要了解技术细节。 效果图 二、实现思路 总体思路: 用户通过Gradio界面上…...
