leetCode 1143.最长公共子序列 动态规划 + 滚动数组
1143. 最长公共子序列 - 力扣(LeetCode)
给定两个字符串 text1 和 text2,返回这两个字符串的最长 公共子序列 的长度。如果不存在 公共子序列 ,返回 0 。
一个字符串的 子序列 是指这样一个新的字符串:它是由原字符串在不改变字符的相对顺序的情况下删除某些字符(也可以不删除任何字符)后组成的新字符串。
- 例如,
"ace"是"abcde"的子序列,但"aec"不是"abcde"的子序列。
两个字符串的 公共子序列 是这两个字符串所共同拥有的子序列。
示例 1:
输入:text1 = "abcde", text2 = "ace" 输出:3 解释:最长公共子序列是 "ace" ,它的长度为 3 。
示例 2:
输入:text1 = "abc", text2 = "abc" 输出:3 解释:最长公共子序列是 "abc" ,它的长度为 3 。
示例 3:
输入:text1 = "abc", text2 = "def" 输出:0 解释:两个字符串没有公共子序列,返回 0 。
>>思路和分析
本题和 leetCode 718.最长重复子数组 区别在于这里不要求是连续的了,但是要有相对顺序,即:"ace" 是 "abcde" 的子序列 ,但是 "aec" 不是 "abcde" 的子序列
>>动规五部曲
1.确定dp数组(dp table)以及下标的含义
dp[i][j] : 长度为 [0,i-1] 的字符串 text1 与长度为 [0,j-1]的字符串text2的最长公共子序列为dp[i][j]
2.确定递推公式
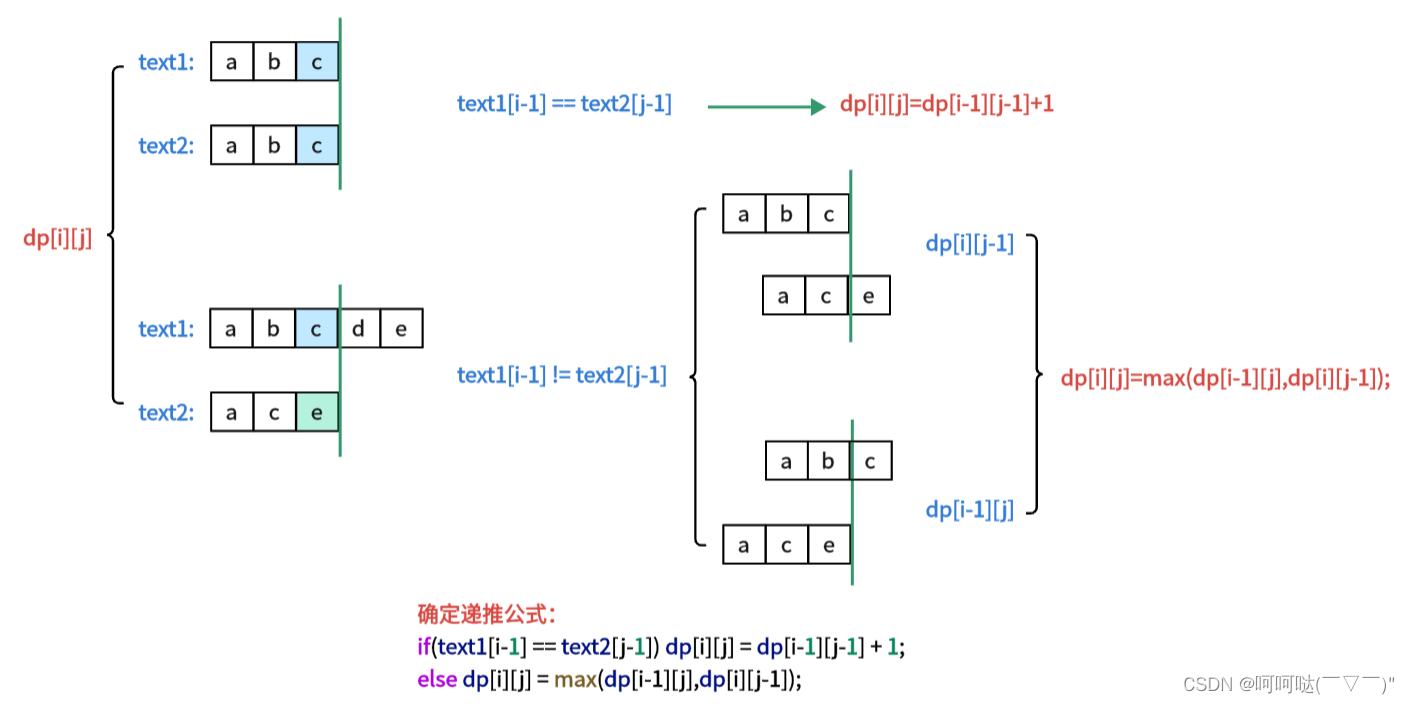
思考:有哪些方向可以推出dp[i][j]?
- text1[i-1] == text[j-1]时,dp[i][j]=dp[i-1][j-1]+1
- text1[i-1] != text[j-1]时,分两种情况讨论:
- 情况①: 不看e了,考虑c,就是abc和ac。这两个原字符串的最长公共子序列也可能是abc和ac的最长公共子序列。因为c和e明显不相同,那么可不考虑e了
- 情况②: 同理,也可以不看c了,考虑e,就是ab和ace。这两个字符串也可能是两个原字符串的最长公共子序列
- 那么这两种情况应该怎么取呢?这两种情况都有可能是dp[i][j],那么
- dp[i][j] = max(dp[i][j-1],dp[i-1][j]);
- 情况①对应dp[i][j-1]
- 情况②对应dp[i-1][j]
- dp[i][j] = max(dp[i][j-1],dp[i-1][j]);
确定递推公式:
if(text1[i-1] == text2[j-1]) dp[i][j] = dp[i-1][j-1] + 1;
else dp[i][j] = max(dp[i-1][j],dp[i][j-1]);3.dp数组初始化
- dp[i][0] 应该初始化为0,因为 test1[0,i-1] 和空串的最长公共子序列是0
- dp[0][j] 同理也为0
- 其他下标都是随着递推公式逐步覆盖,初始为多少都可以
故统一初始为0,代码如下:
vector<vector<int>> dp(text1.size() + 1, vector<int>(text2.size() + 1, 0));
4.确定遍历顺序
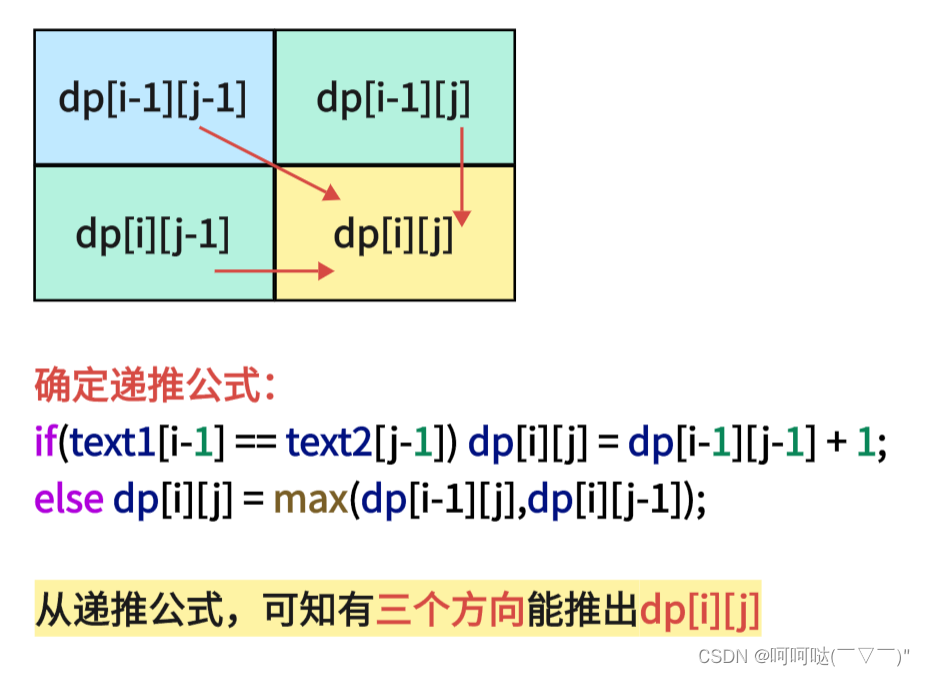
那么为了在递推的过程中,这三个方向都是经过计算的数值,所以要从前向后,从上到下来遍历这个矩阵
5.举例推导dp数组
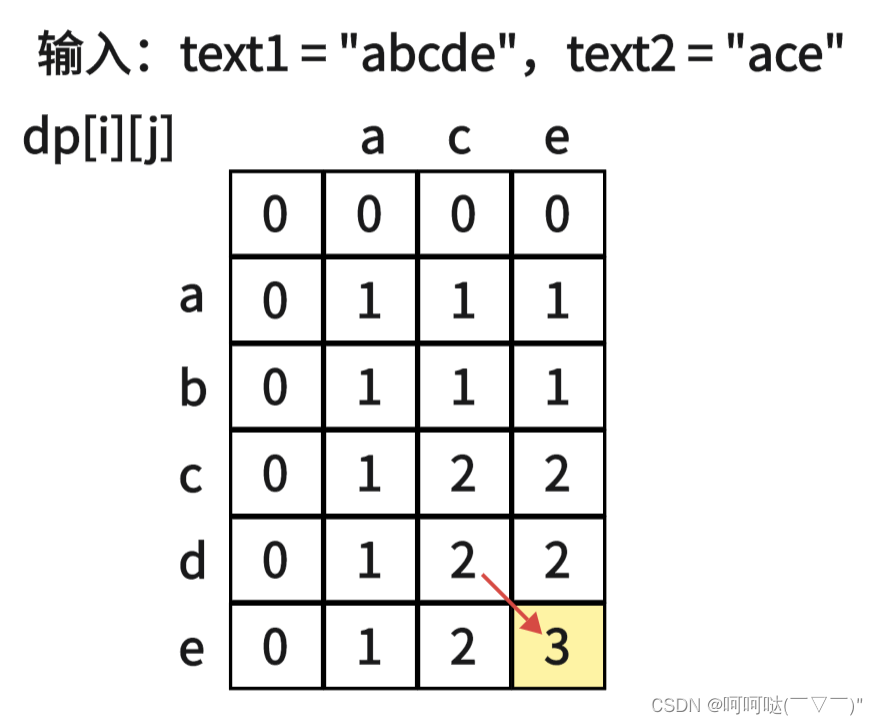
由上图可看到dp[text1.size()][text2.size()]为最终结果
class Solution {
public:int longestCommonSubsequence(string text1, string text2) {vector<vector<int>> dp(text1.size() + 1, vector<int>(text2.size() + 1, 0));for (int i = 1; i <= text1.size(); i++) {for (int j = 1; j <= text2.size(); j++) {if (text1[i - 1] == text2[j - 1]) {dp[i][j] = dp[i - 1][j - 1] + 1;} else {dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);}}}return dp[text1.size()][text2.size()];}
};- 时间复杂度: O(n * m),其中 n 和 m 分别为 text1 和 text2 的长度
- 空间复杂度: O(n * m)
>>优化空间复杂度
class Solution {
public:// 滚动数组int longestCommonSubsequence(string text1, string text2) {vector<int> dp(text2.size() + 1, 0);for(int i=1;i<=text1.size();i++) {int pre = dp[0];for(int j=1;j<=text2.size();j++) {int tmp = dp[j];if(text1[i-1] == text2[j-1]) dp[j] = pre + 1;else dp[j] = max(dp[j-1],dp[j]);pre = tmp;}}return dp[text2.size()];}
};- 时间复杂度: O(n * m),其中 n 和 m 分别为 text1 和 text2 的长度
- 空间复杂度: O(m)
参考文章和视频:
动态规划子序列问题经典题目 | LeetCode:1143.最长公共子序列_哔哩哔哩_bilibili 代码随想录 (programmercarl.com)
来自代码随想录课堂截图:

相关文章:

leetCode 1143.最长公共子序列 动态规划 + 滚动数组
1143. 最长公共子序列 - 力扣(LeetCode) 给定两个字符串 text1 和 text2,返回这两个字符串的最长 公共子序列 的长度。如果不存在 公共子序列 ,返回 0 。 一个字符串的 子序列 是指这样一个新的字符串:它是由原字符串…...

【C++ Miscellany】继承体系非尾端类设计为抽象类
部分赋值问题 用软件来处理两种动物:蜥蜴和鸡 class Animal { public:Animal& operator (const Animal& rhs);... };class Lizard: public Animal { public:Lizard& operator (const Lizard& rhs);... };class Chicken: public Animal {Chicken…...
Leetcode236. 二叉树的最近公共祖先
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。 百度百科中最近公共祖先的定义为:“对于有根树 T 的两个节点 p、q,最近公共祖先表示为一个节点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖…...
Swift SwiftUI CoreData 过滤数据 2
预览 Code import SwiftUI import CoreDatastruct HomeSearchView: View {Environment(\.dismiss) var dismissState private var search_value ""FetchRequest(entity: Bill.entity(),sortDescriptors: [NSSortDescriptor(keyPath: \Bill.c_at, ascending: false)…...
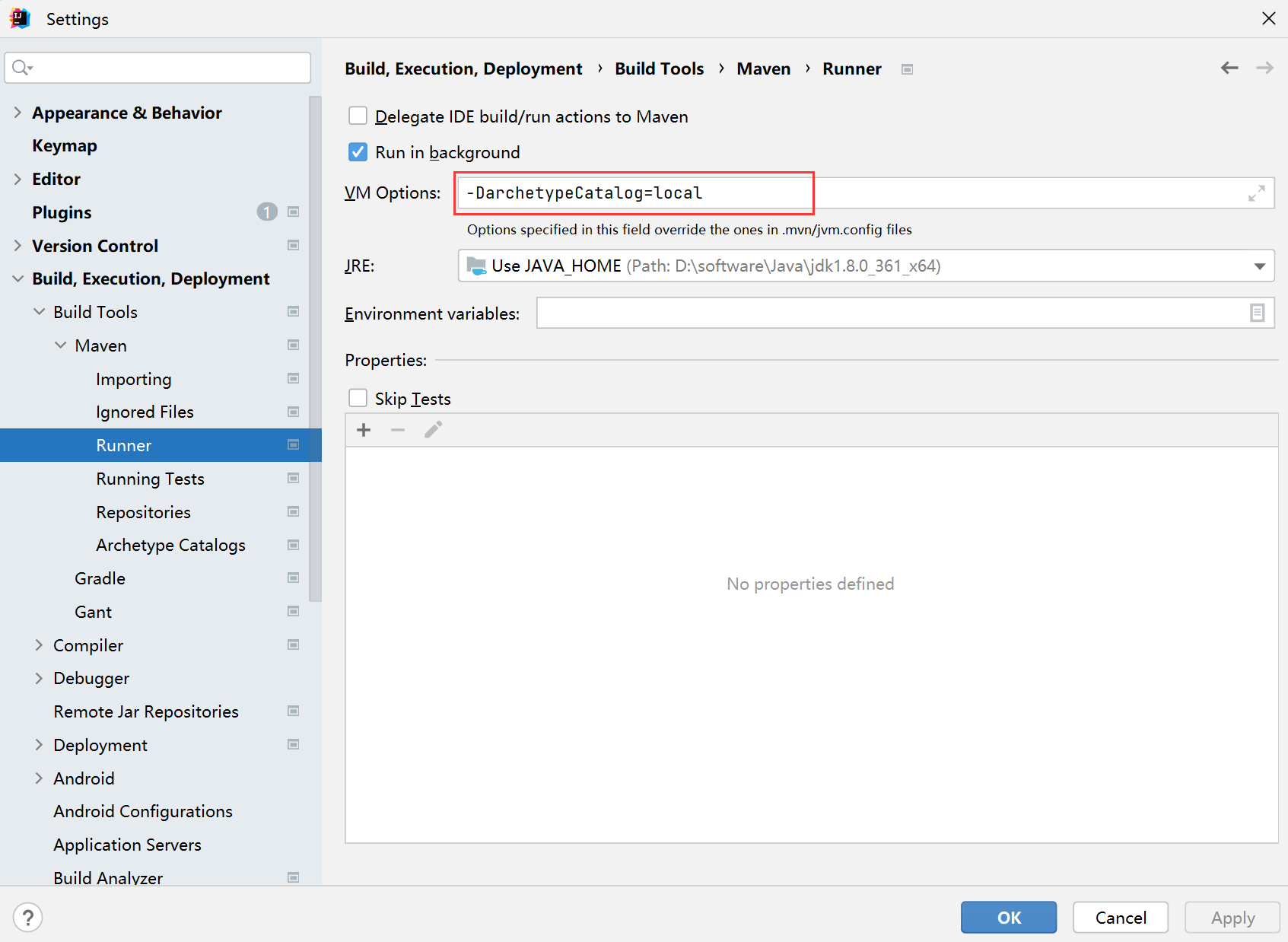
解决maven骨架加载慢问题(亲测解决)
1、下载archetype-catalog.xml 网站 : https://repo.maven.apache.org/maven2/ 2、放在这个文件夹下面 3、setting–>build–>Runner : -DarchetypeCataloglocal...

Android---java内存模型与线程
Java 内存模型翻译自 Java Memory Model,简称 JMM。它所描述的是多线程并发、CPU 缓存等方面的内容。 在每一个线程中,都会有一块内部的工作内存,这块内存保存了主内存共享数据的拷贝副本。但在 Java 线程中并不存在所谓的工作内存࿰…...

23.10.7.sql 里面的DISTINCT
例如: SELECT DISTINCT t.container_no FROM biz_inventory_task_detail t 这里distinct干嘛的 解释: DISTINCT是一个关键字,用于在SELECT语句中返回唯一不重复的值。 在这个查询中,使用DISTINCT关键字,是为了返回biz…...

mysql面试题38:count(1)、count(*) 与 count(列名) 的区别
该文章专注于面试,面试只要回答关键点即可,不需要对框架有非常深入的回答,如果你想应付面试,是足够了,抓住关键点 面试官: count(1)、count(*) 与 count(列名) 的区别 当使用COUNT函数进行数据统计时&…...

nodejs+vue+elementui大学生心理健康管理系统
简单的说 Node.js 就是运行在服务端的 JavaScript。 前端技术:nodejsvueelementui 前端:HTML5,CSS3、JavaScript、VUE本大学生心理健康管理系统使用简洁的框架结构,专门用于用户咨询心理专家,系统具有方便性、灵活性、应用性。于是…...
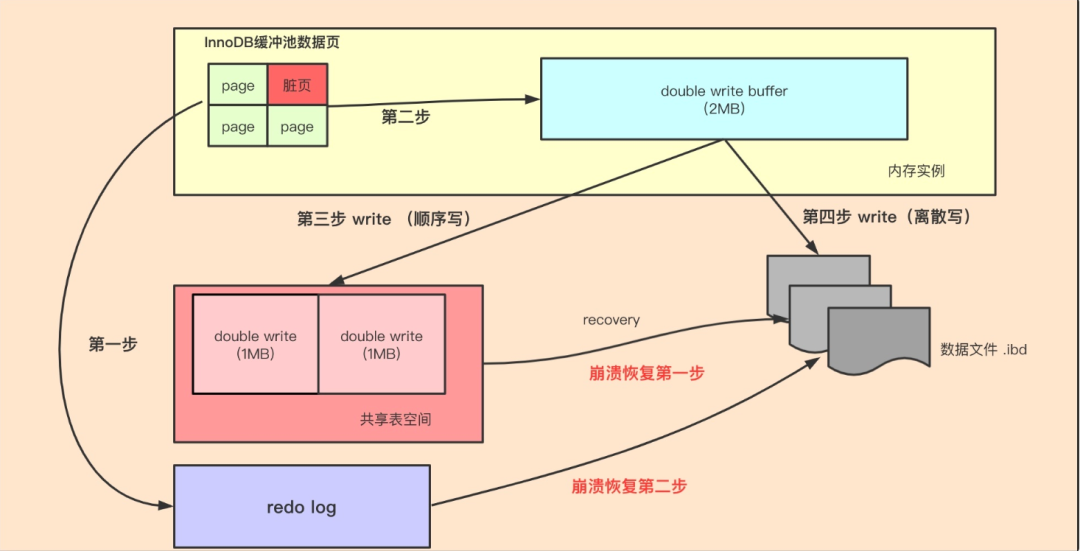
【MySQL】深入解析MySQL双写缓冲区
原创不易,注重版权。转载请注明原作者和原文链接 文章目录 为什么需要Doublewrite BufferDoublewrite Buffer原理Doublewrite Buffer和redo logDoublewrite Buffer相关参数总结 在数据库系统的世界中,保障数据的完整性和稳定性是至关重要的任务。为了实现…...
u-boot 编译与运行
文章目录 u-boot 编译与运行环境配置ubuntu 版本qemu 版本u-boot 版本(master)交叉工具链版本 u-boot 源码下载生成配置文件报错情况一报错情况2 u-boot 配置编译编译脚本编译报错解决编译日志编译产物 运行 u-boot 编译与运行 本文主要介绍 u-boot 编译…...

C++QT-day2
#include <bits/stdc.h>/*自己封装一个矩形类(Rect),拥有私有属性:宽度(width)、高度(height),定义公有成员函数:初始化函数:void init(int w, int h)更改宽度的函数:set_w(int w)更改高度的函数:set_h(int h)输出该矩形的周长和面积函数:void sho…...
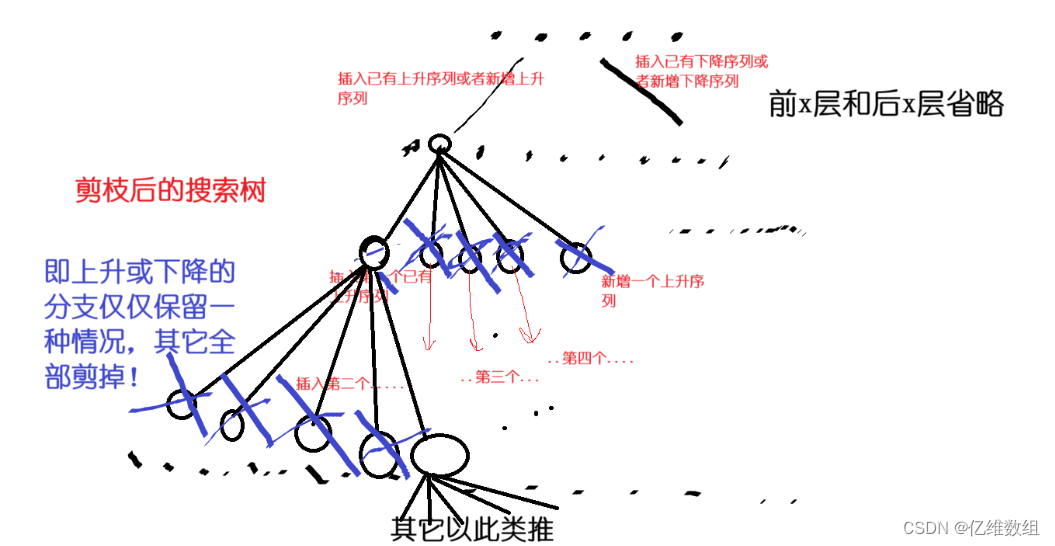
【Acwing187】导弹防御系统(LIS+剪枝+贪心+dfs+迭代加深)
题目描述 看本文需要准备的知识 1.最长上升子序列(lis)的算法思想和算法模板 2.acwing1010拦截导弹(lis贪心)题解 本题题解,需要知道这种贪心算法 3.简单了解dfs暴力搜索、剪枝、搜索树等概念 思路讲解 dfs求最…...
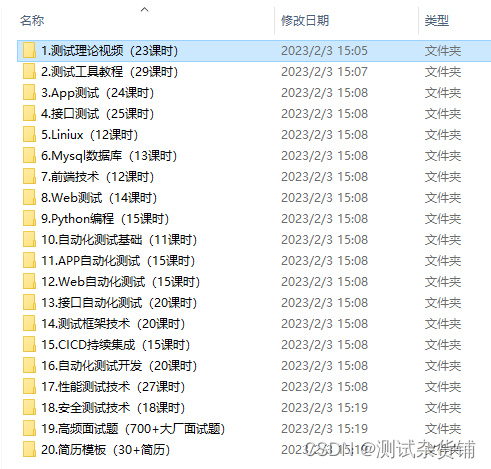
字节大佬带你五分钟掌握接口自动化测试框架
今天,我们来聊聊接口自动化测试是什么?如何开始?接口自动化测试框架怎么做? 自动化测试 自动化测试,这几年行业内的热词,也是测试人员进阶的必备技能,更是软件测试未来发展的趋势。 特别是在…...
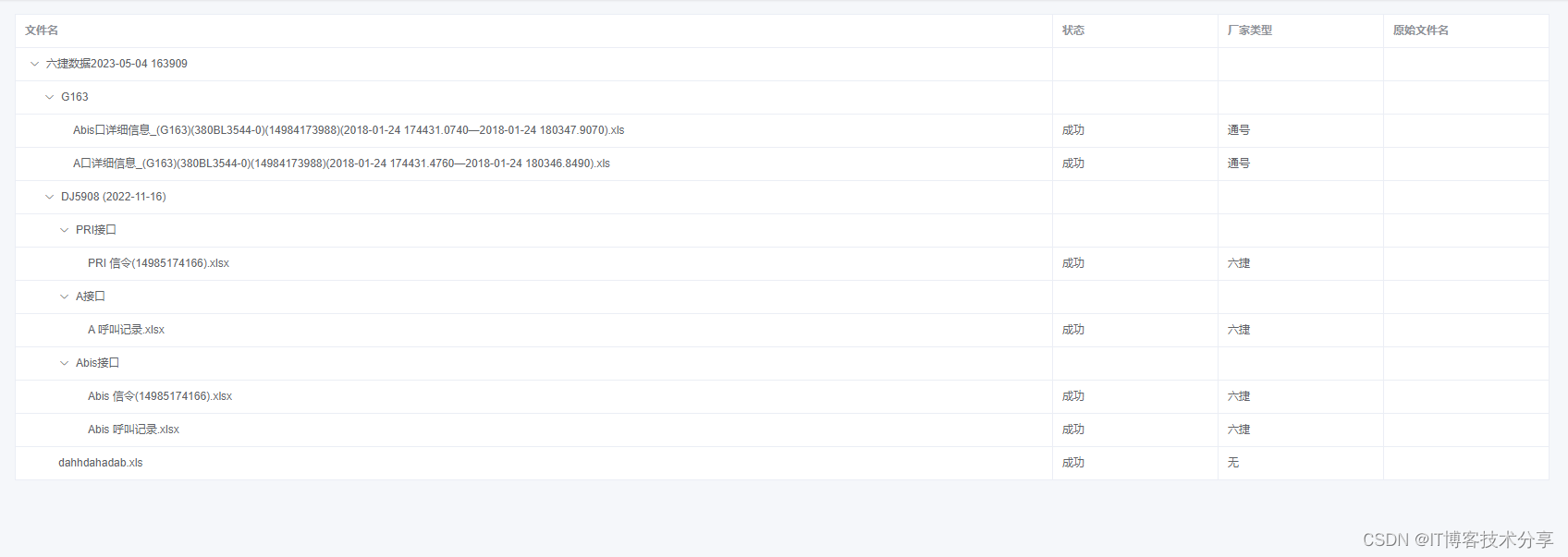
上传文件夹里面的文件后,按树结构的table表格展示
1. 先处理最简单的 原始数据大概是这样: let fileArr [{progress: 100,status: 成功,type: 通号,webkitRelativePath: "六捷数据2023-05-04 163909/G163/Abis口详细信息_(G163)(380BL3544-0)(14984173988)(2018-01-24 174431.0740—2018-01-24 180347.9070).xls"…...
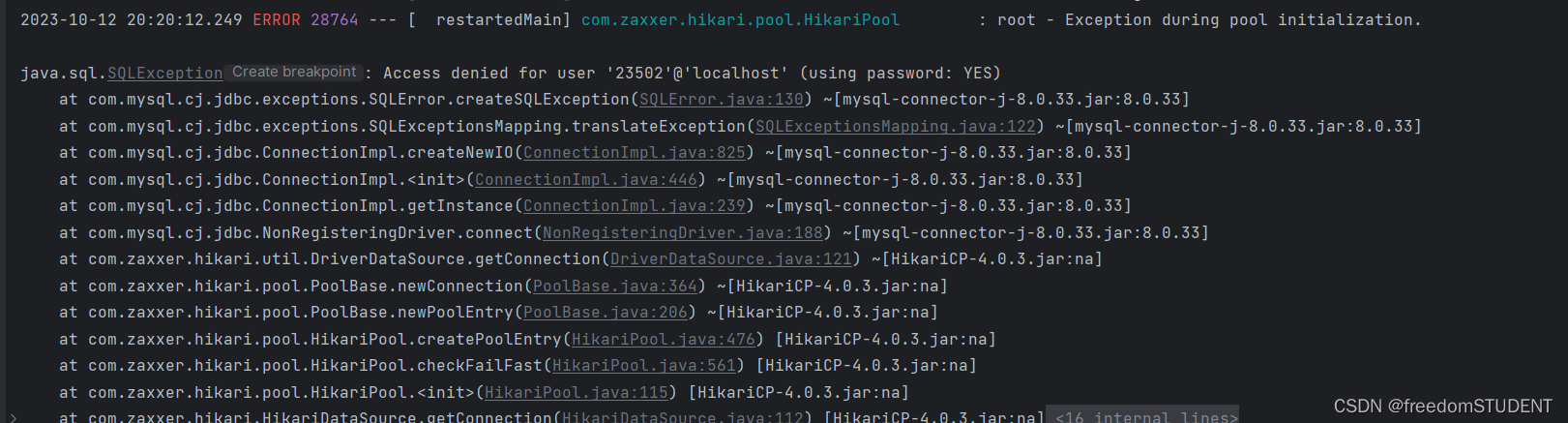
【error】root - Exception during pool initialization
报错提示:root - Exception during pool initialization. 错误原因: 配置数据库出错 我的错误配置: spring.datasource.urljdbc:mysql://localhost:3306/springboot?serverTimezoneGMT spring.datasource.nameroot spring.datasource.pass…...

【重拾C语言】九、再论函数(指针、数组、结构体作参数;函数值返回指针、结构体;作用域)
目录 前言 九、再论函数 9.1 参数 9.1.1 参数的传递规则 9.1.2 指针作参数 9.1.3 数组作参数 9.1.4 结构体作参数 a. 直接用结构体变量作函数参数 b. 用指向结构体变量的指针作函数参数 9.2 函数值 9.2.1 返回指针值 9.2.2 返回结构体值 a. 返回结构体值 b. 返回…...

Spring WebClient 基于响应式编程模型的HTTP客户端
一、简介 WebClient是一个非阻塞的、可扩展的、基于Reactive Streams规范的HTTP客户端。它提供了一种简洁的方式来进行HTTP请求,并且可以很好地与其他Spring组件集成。WebClient支持同步和异步操作,使得它非常适合用于构建响应式应用程序。 WebClient允…...

IP真人识别方法与代理IP检测技术
随着互联网的发展,IP地址在网络安全和数据分析中扮演着重要的角色。为了维护网络的安全性和识别真实用户,IP地址的真实性和来源成为了一个关键问题。 什么是IP真人识别? IP真人识别是一种技术,旨在确定IP地址背后的用户是否为真实…...
MySQL 面试知识脑图 初高级知识点
脑图下载地址:https://mm.edrawsoft.cn/mobile-share/index.html?uuid18b10870122586-src&share_type1 sql_mode 基本语法及校验规则 ONLY_FULL_GROUP_BY 对于GROUP BY聚合操作,如果在SELECT中的列,没有在GROUP BY中出现ÿ…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

SpringTask-03.入门案例
一.入门案例 启动类: package com.sky;import lombok.extern.slf4j.Slf4j; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.cache.annotation.EnableCach…...

Docker 本地安装 mysql 数据库
Docker: Accelerated Container Application Development 下载对应操作系统版本的 docker ;并安装。 基础操作不再赘述。 打开 macOS 终端,开始 docker 安装mysql之旅 第一步 docker search mysql 》〉docker search mysql NAME DE…...

GruntJS-前端自动化任务运行器从入门到实战
Grunt 完全指南:从入门到实战 一、Grunt 是什么? Grunt是一个基于 Node.js 的前端自动化任务运行器,主要用于自动化执行项目开发中重复性高的任务,例如文件压缩、代码编译、语法检查、单元测试、文件合并等。通过配置简洁的任务…...

如何更改默认 Crontab 编辑器 ?
在 Linux 领域中,crontab 是您可能经常遇到的一个术语。这个实用程序在类 unix 操作系统上可用,用于调度在预定义时间和间隔自动执行的任务。这对管理员和高级用户非常有益,允许他们自动执行各种系统任务。 编辑 Crontab 文件通常使用文本编…...

uniapp 开发ios, xcode 提交app store connect 和 testflight内测
uniapp 中配置 配置manifest 文档:manifest.json 应用配置 | uni-app官网 hbuilderx中本地打包 下载IOS最新SDK 开发环境 | uni小程序SDK hbulderx 版本号:4.66 对应的sdk版本 4.66 两者必须一致 本地打包的资源导入到SDK 导入资源 | uni小程序SDK …...
