HDLbits: ece241 2013 q12 // Exams/m2014 q4k
两道题目,有一样的问题:
第一道:ece241 2013 q12
下面的代码错误,一直没看出来哪里有问题:
module top_module (input clk,input enable,input S,input A, B, C,output Z ); reg [7:0] q;dff dff_1(clk,enable,S,q[0]);dff dff_2(clk,enable,q[0],q[1]);dff dff_3(clk,enable,q[1],q[2]);dff dff_4(clk,enable,q[2],q[3]);dff dff_5(clk,enable,q[3],q[4]);dff dff_6(clk,enable,q[4],q[5]);dff dff_7(clk,enable,q[5],q[6]);dff dff_8(clk,enable,q[6],q[7]);always@(*)begincase({A,B,C})3'b000: Z=q[0];3'b001: Z=q[1];3'b010: Z=q[2];3'b011: Z=q[3];3'b100: Z=q[4];3'b101: Z=q[5];3'b110: Z=q[6];3'b111: Z=q[7];endcaseend
endmodulemodule dff (input clk,input ena,input d,output q ); always@(posedge clk)beginif(ena)q <= d;elseq <= q; end
endmodule
同样思路的另外一套代码就没问题:
module top_module (input clk,input enable,input S,input A, B, C,output Z ); reg [7:0]Q;dfif dff_u0(.clk(clk), .d(S), .enable(enable), .q(Q[0]));dfif dff_u1(.clk(clk), .d(Q[0]), .enable(enable), .q(Q[1]));dfif dff_u2(.clk(clk), .d(Q[1]), .enable(enable), .q(Q[2]));dfif dff_u3(.clk(clk), .d(Q[2]), .enable(enable), .q(Q[3]));dfif dff_u4(.clk(clk), .d(Q[3]), .enable(enable), .q(Q[4]));dfif dff_u5(.clk(clk), .d(Q[4]), .enable(enable), .q(Q[5]));dfif dff_u6(.clk(clk), .d(Q[5]), .enable(enable), .q(Q[6]));dfif dff_u7(.clk(clk), .d(Q[6]), .enable(enable), .q(Q[7]));always@(*)begincase({A,B,C})3'd0:Z=Q[0];3'd1:Z=Q[1];3'd2:Z=Q[2];3'd3:Z=Q[3];3'd4:Z=Q[4];3'd5:Z=Q[5];3'd6:Z=Q[6];3'd7:Z=Q[7];endcaseendendmodulemodule dfif(input clk,input d,input enable,output q
);always@(posedge clk)beginif(enable)beginq<=d; endelse beginq<=q;endend
endmodule
第二道题目:Exams/m2014 q4k,也是这种情况
下面的代码错误,一直没看出来哪里有问题:
module top_module (input clk,input resetn, // synchronous resetinput in,output out);wire q1,q2,q3;dff dff_1(clk, resetn, in, q1);dff dff_2(clk, resetn, q1, q2);dff dff_3(clk, resetn, q2, q3);dff dff_4(clk, resetn, q3, out);endmodulemodule dff(input clk,input r,input d,output q);always@(posedge clk)beginif(!r)q <= 0;elseq <= d;end
endmodule
同样思路的另外一套代码就没问题:
module top_module (input clk,input resetn, // synchronous resetinput in,output out);wire q0,q1,q2;my_sr inst0(in,clk,resetn,q0);my_sr inst1(q0,clk,resetn,q1);my_sr inst2(q1,clk,resetn,q2);my_sr inst3(q2,clk,resetn,out);endmodulemodule my_sr(input D,input clk,input R,output Q
);always@(posedge clk)beginif(R==1'b0)Q<=0;elseQ<=D;end
endmodule相关文章:

HDLbits: ece241 2013 q12 // Exams/m2014 q4k
两道题目,有一样的问题: 第一道:ece241 2013 q12 下面的代码错误,一直没看出来哪里有问题: module top_module (input clk,input enable,input S,input A, B, C,output Z ); reg [7:0] q;dff dff_1(clk,enable,S,q[…...
)
vue3模板-vscode设置(语法糖)
选择菜单里的 文件 > 首选项 > 用户代码片段 vscode模板 {"Print to conaole":{"prefix": "v-ts", //在新建立的页面中输入C就会有智能提示,Tab就自动生成好了"body": ["<template>"," <…...

RFID超高频读写器的特点和应用
RFID读写器根据不同的工作频段可以分为高频读写器和超高频读写器,高频读写器通常在13.56Mhz频段工作,超高频读写器一般在860-960M Hz频段工作。下面我们就来为大家详细介绍一下,超高频读写器的特点和实际应用。 超高频读写器的工作原理 超高频…...

诡异事件:开发的安卓摄像头应用突然不能保存图片,回滚代码都查不出来
昨天对摄像头应用进行了大规模修改,在一个工程中,同时编译两个app。一番辛苦工作之后,成功。进行了测试,发现诡异的事情:照相无法保存! 那怎么办?赶紧增加搞权限,没用。 逐个版本回滚…...
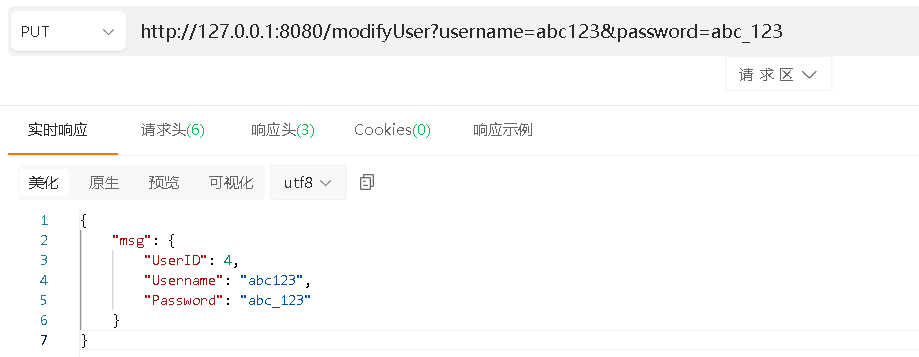
validator库的使用详解
目录 基本使用前言请求模型的定义编写接口及测试 翻译校验错误提示信息自定义错误提示信息的字段名自定义校验规则常见的参数校验字段 基本使用 前言 在做API开发时,需要对请求参数的校验,防止用户的恶意请求。例如日期格式,用户年龄&#x…...
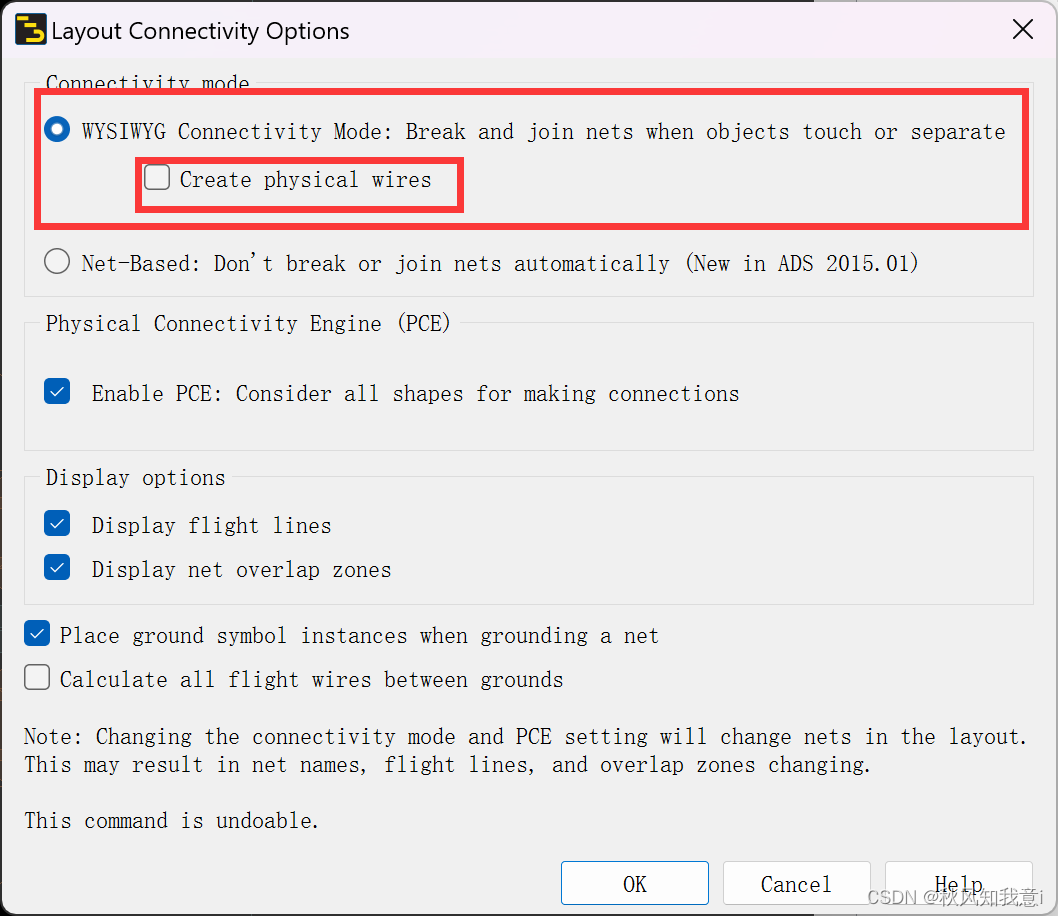
ADS版图中连接提示线设置
ADS版图连接提示线设置 简述solve 简述 在ADS版中连接提示线设置,如下图1所示,有点类似于AD中“金线”,提示同一网络的焊盘,但在ads中,是产生了同一层的wire,证据如图2所示。如果没有设置的话,…...

【MySQL】内置函数——数学函数+其他函数
文章目录 一. 数字函数二. 其他函数 一. 数字函数 函数名称描述abs()绝对值函数bin()十进制转换二进制hex()转换成十六进制conv(number,from_base,to_base)将number从from_base转换成to_base进制ceiling()向上取整floor()向下取整format(number,decimal_places)格式化…...

Ubuntu 23.10 Beta 镜像开放下载
导读Canonical放出了 Ubuntu 23.10 Beta 镜像,此外 Edubuntu、Kubuntu、Lubuntu、Ubuntu Budgie、Ubuntu Cinnamon、Ubuntu Kylin、Ubuntu MATE、Ubuntu Studio、Ubuntu Unity 和 Xubuntu 等风味版本也同步放出镜像。 近日消息,Canonical 放出了 Ubuntu …...

mybatispagehelp嵌套分页处理
1.定义嵌套vo类 /*** 用户中心,我的订单列表VO*/ public class MyOrdersVO {private String orderId;private Date createdTime;private Integer payMethod;private Integer realPayAmount;private Integer postAmount...
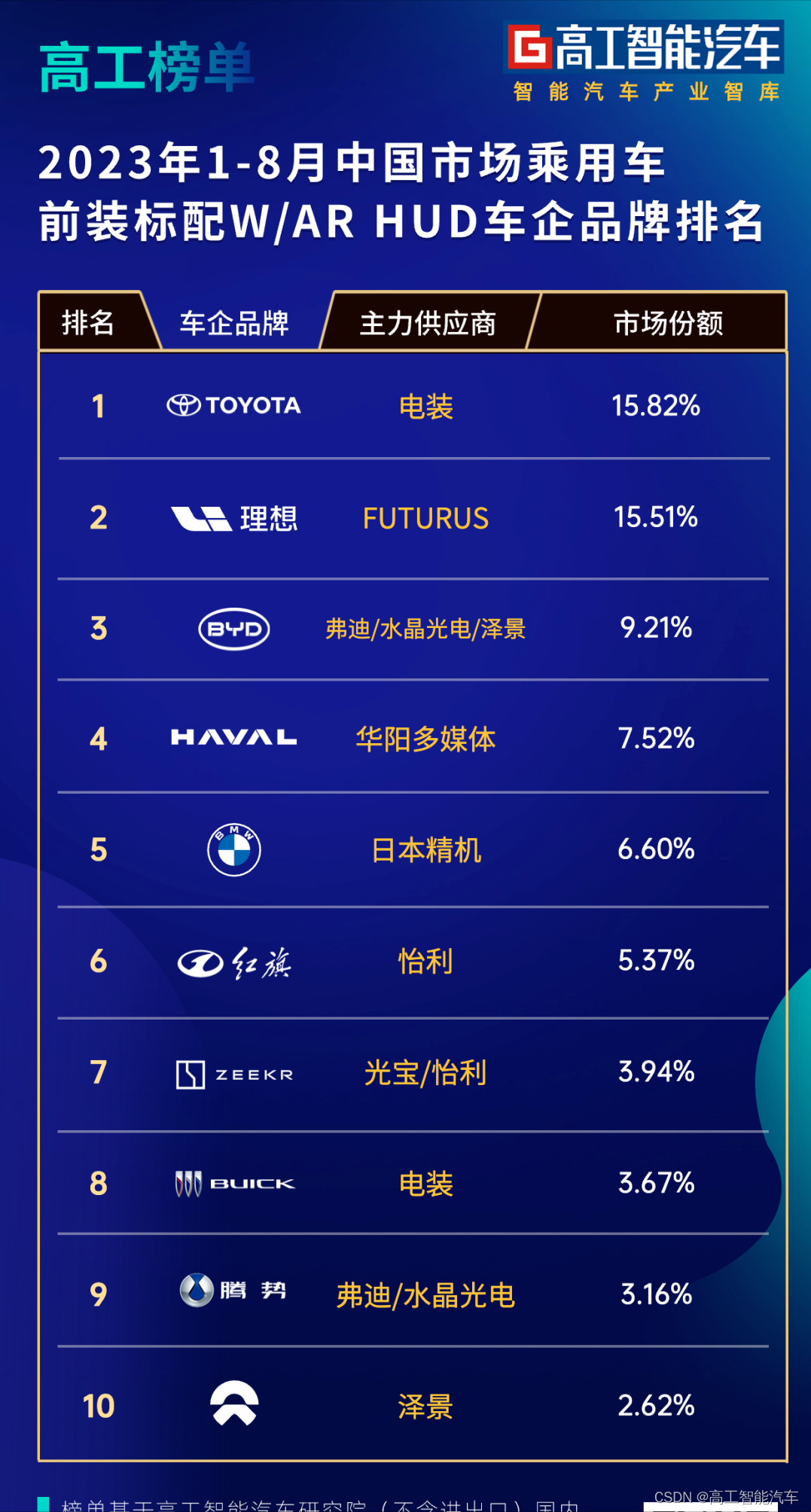
增速波动!W「下」AR「上」!HUD前装供应商比拼硬核能力
作为汽车智能座舱人机交互的新配置之一,HUD(抬头显示)市场在经历一波快速增长周期后,进入调整阶段。 本周,高工智能汽车研究院发布数据显示,2023年8月,中国市场(不含进出口ÿ…...
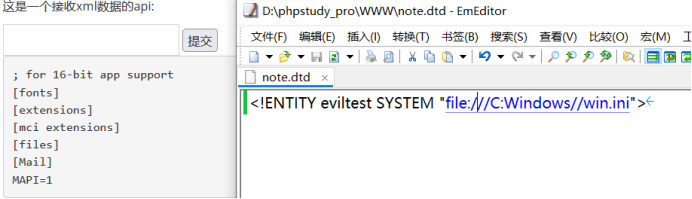
XXE漏洞复现实操
文章目录 一、漏洞原理二、验证payload三、没有回显时的验证四、漏洞特征五、读取文件六、Base64加密读取七、端口检测八、使用php检测端口九、dtd外部实体读取文件十、Xxe漏洞防御 一、漏洞原理 (1)XXE漏洞全称XML External Entity Injection,即xmI外部实体注入漏…...
github创建个人网页登录后404无法显示的问题
1.首先必须要有内容,默认是会找index.html文件,找不到该文件会找readme.md文件,也就是说最简单的方法是,创建了与用户名同名的repository后username.github.io后,添加一个readme.md文件,得在readme里打点字…...
MySQL——源码安装教程(初版)
MySQL 一、MySQL的安装1、RPM2、二进制3、源码 二、源码安装方式三、安装过程1、上传源码包2、解压当前文件并安装更新依赖3、对MySQL进行编译安装 一、MySQL的安装 首先这里我来介绍下MySQL的几种安装方式: 一共三种,RPM安装包、二进制包安装以及源码安…...

1.1.C++项目:仿muduo库实现并发服务器之any类的设计
文章目录 一、思想二、框架三、代码 一、思想 每⼀个Connection对连接进行管理,最终都不可避免需要涉及到应用层协议的处理,因此在Connection中需要设置协议处理的上下文来控制处理节奏。但是应用层协议千千万,为了降低耦度,这个…...

linux项目启动脚本start.sh和stop.sh停止脚本
start脚本示例 MAIN_CLASSCLASSPATH.;JVM_PARMS""export APP_HOME$(dirname $(pwd))export APP_APPS$APP_HOME/appsexport APP_RESOURCES$APP_HOME/confexport APP_LIB$APP_HOME/libexport APP_LOG$APP_HOME/logs;export APP_NAME$(basename $APP_HOME)function mak…...
Avalonia常用小控件Svg
1.项目下载地址:https://gitee.com/confusedkitten/avalonia-demo 2.UI库Semi.Avalonia,项目地址 https://github.com/irihitech/Semi.Avalonia 3.SVG库,Avalonia.Svg.Skia,项目地址 https://github.com/wieslawsoltes/Svg.Ski…...

设计模式-行为型模式
文章目录 一、模板方法模式二、策略模式三、命令模式四、责任链模式五、状态模式六、观察者模式七、中介者模式八、迭代器模式九、访问者模式十、备忘录模式十一、解释器模式 一、模板方法模式 定义一个操作中的算法骨架,而将算法的一些步骤延迟到子类中࿰…...
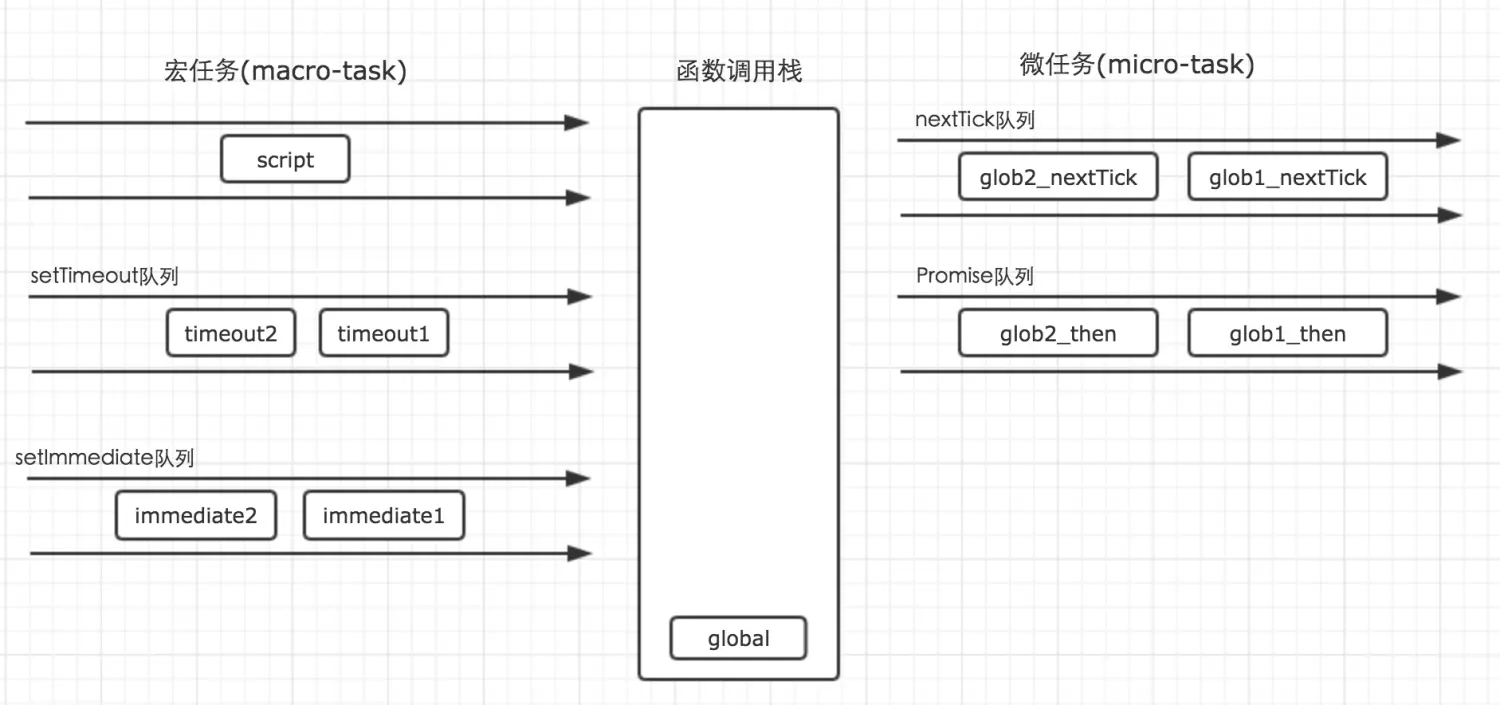
【EventLoop】问题一次搞定
📍 JS的事件循环机制恐怕是大多数前端开发者头顶上的一座大山之一,最近通过拜读两篇文档,对eventloop进行了深刻的理解;通过这篇文档对要点进行总结; article1: 波神的这篇eventLoop文章适合反复重温&…...
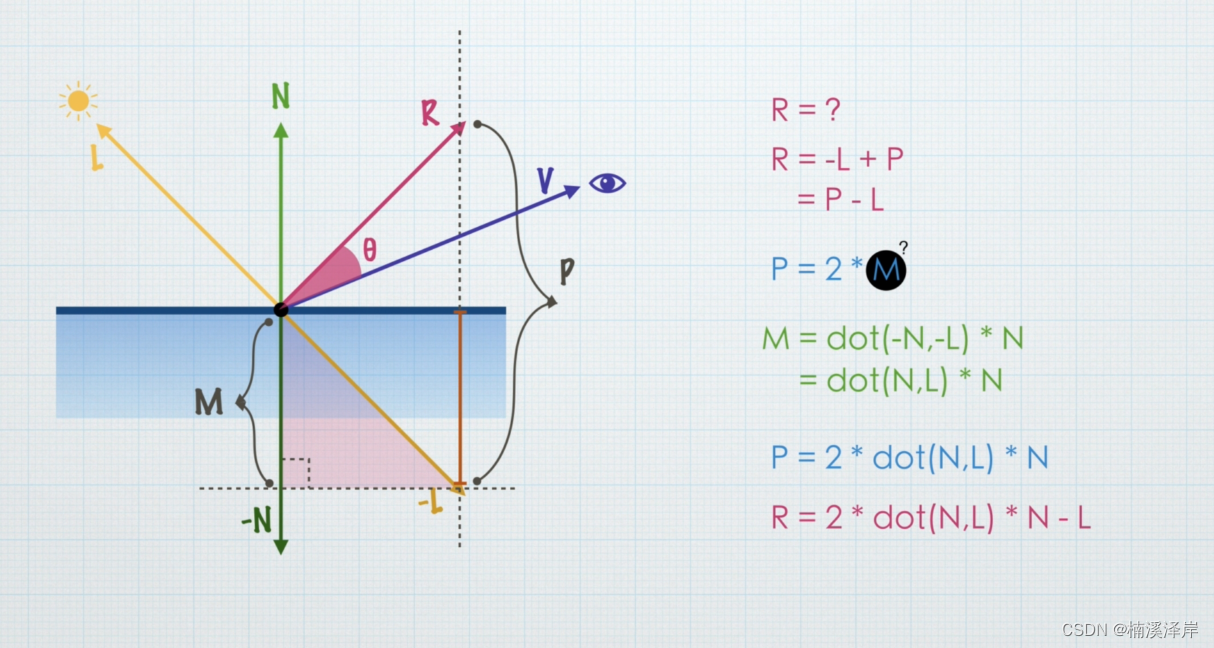
Unity中Shader光照模型Phong
文章目录 前言一、Phong光照模型二、图示解释Phone光照模型1、由图可得,R 可以由 -L 加上 P 得出2、P等于2*M3、因为 N 和 L 均为单位向量,所以 M 的模可以由 N 和 L得出4、得到M的模后,乘以 单位向量N,得到M5、最后得出 P 和 R 前…...
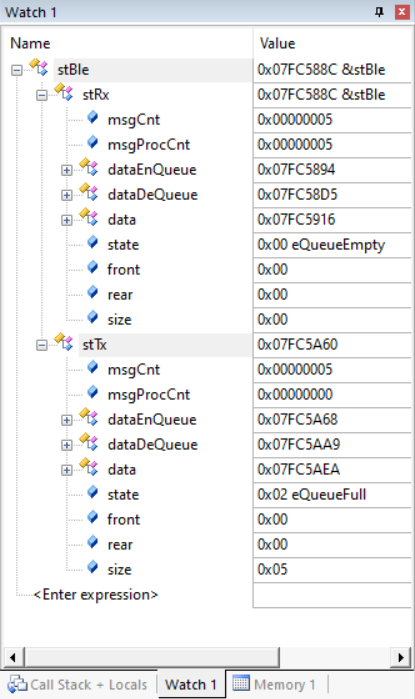
消息队列缓存,以蓝牙消息服务为例
前言 消息队列缓存,支持阻塞、非阻塞模式;支持协议、非协议模式 可自定义消息结构体数据内容 使用者只需设置一些宏定义、调用相应接口即可 这里我用蓝牙消息服务举例 有纰漏请指出,转载请说明。 学习交流请发邮件 1280253714qq.com 原…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...

AI编程--插件对比分析:CodeRider、GitHub Copilot及其他
AI编程插件对比分析:CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展,AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者,分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...

阿里云Ubuntu 22.04 64位搭建Flask流程(亲测)
cd /home 进入home盘 安装虚拟环境: 1、安装virtualenv pip install virtualenv 2.创建新的虚拟环境: virtualenv myenv 3、激活虚拟环境(激活环境可以在当前环境下安装包) source myenv/bin/activate 此时,终端…...

【HarmonyOS 5】鸿蒙中Stage模型与FA模型详解
一、前言 在HarmonyOS 5的应用开发模型中,featureAbility是旧版FA模型(Feature Ability)的用法,Stage模型已采用全新的应用架构,推荐使用组件化的上下文获取方式,而非依赖featureAbility。 FA大概是API7之…...

链式法则中 复合函数的推导路径 多变量“信息传递路径”
非常好,我们将之前关于偏导数链式法则中不能“约掉”偏导符号的问题,统一使用 二重复合函数: z f ( u ( x , y ) , v ( x , y ) ) \boxed{z f(u(x,y),\ v(x,y))} zf(u(x,y), v(x,y)) 来全面说明。我们会展示其全微分形式(偏导…...

ArcGIS Pro+ArcGIS给你的地图加上北回归线!
今天来看ArcGIS Pro和ArcGIS中如何给制作的中国地图或者其他大范围地图加上北回归线。 我们将在ArcGIS Pro和ArcGIS中一同介绍。 1 ArcGIS Pro中设置北回归线 1、在ArcGIS Pro中初步设置好经纬格网等,设置经线、纬线都以10间隔显示。 2、需要插入背会归线…...
