Python接口自动化 —— Json 数据处理实战(详解)

简介
上一篇说了关于json数据处理,是为了断言方便,这篇就带各位小伙伴实战一下。首先捋一下思路,然后根据思路一步一步的去实现和实战,不要一开始就盲目的动手和无头苍蝇一样到处乱撞,撞得头破血流后而放弃了。不仅什么没学习
到,自己的自信心都受到打击了,自己都怀疑自己。其实你是最棒的,天生我材必有用,好了废话不说,进入实战——以查看快递物流接口为例。
大致流程步骤:web页面操作—>抓包看参数和url—>代码模拟接口请求—>取到接口返回结果—>断言
web页面操作
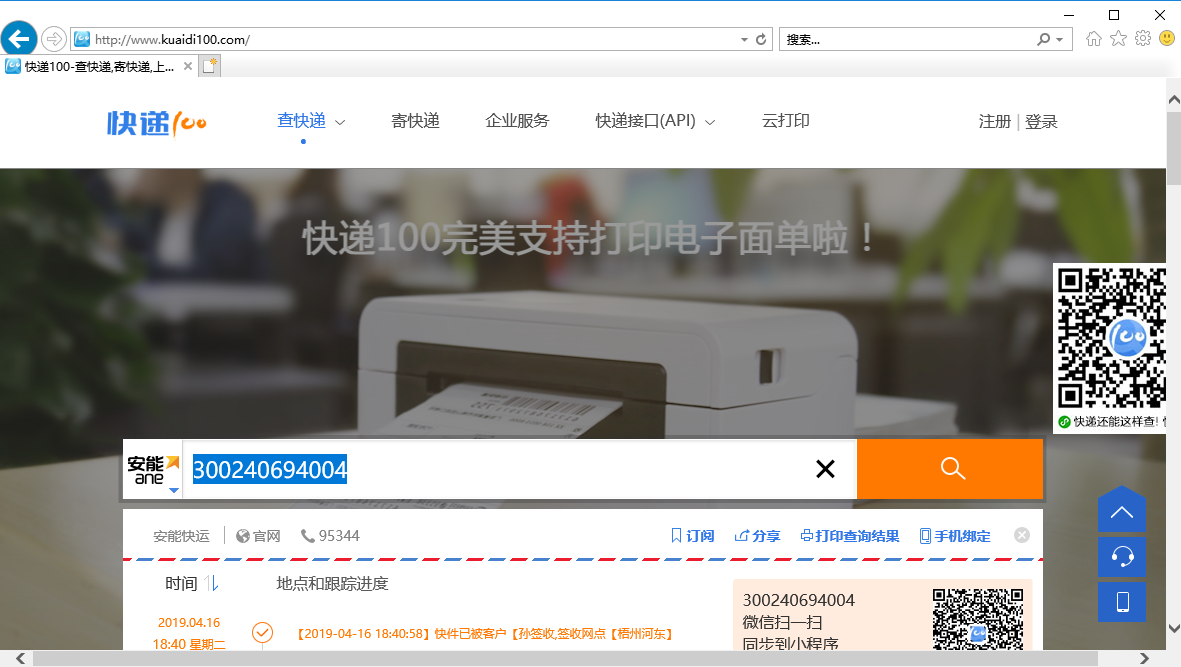
1、浏览器输入快递物流查询url,输入快递单号,点击“查询”
抓包看参数和url
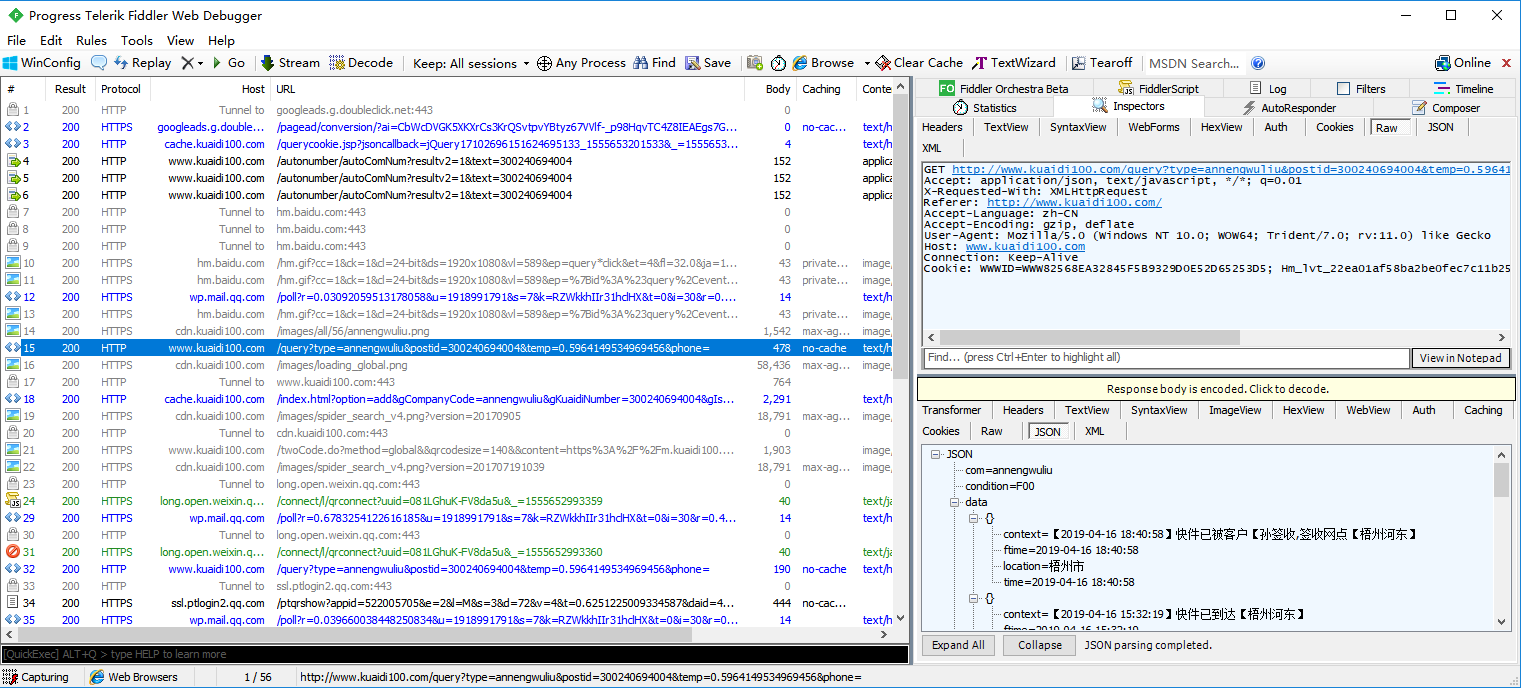
1、点击“查询”,fiddler抓包,查看url和参数
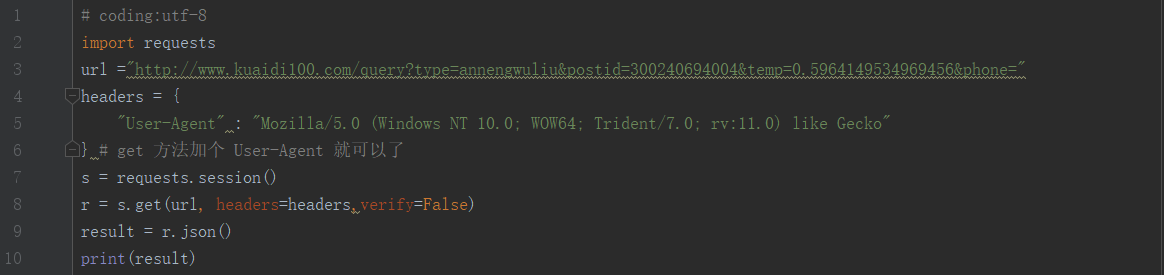
代码模拟接口请求
取到接口返回结果

断言

代码及运行结果
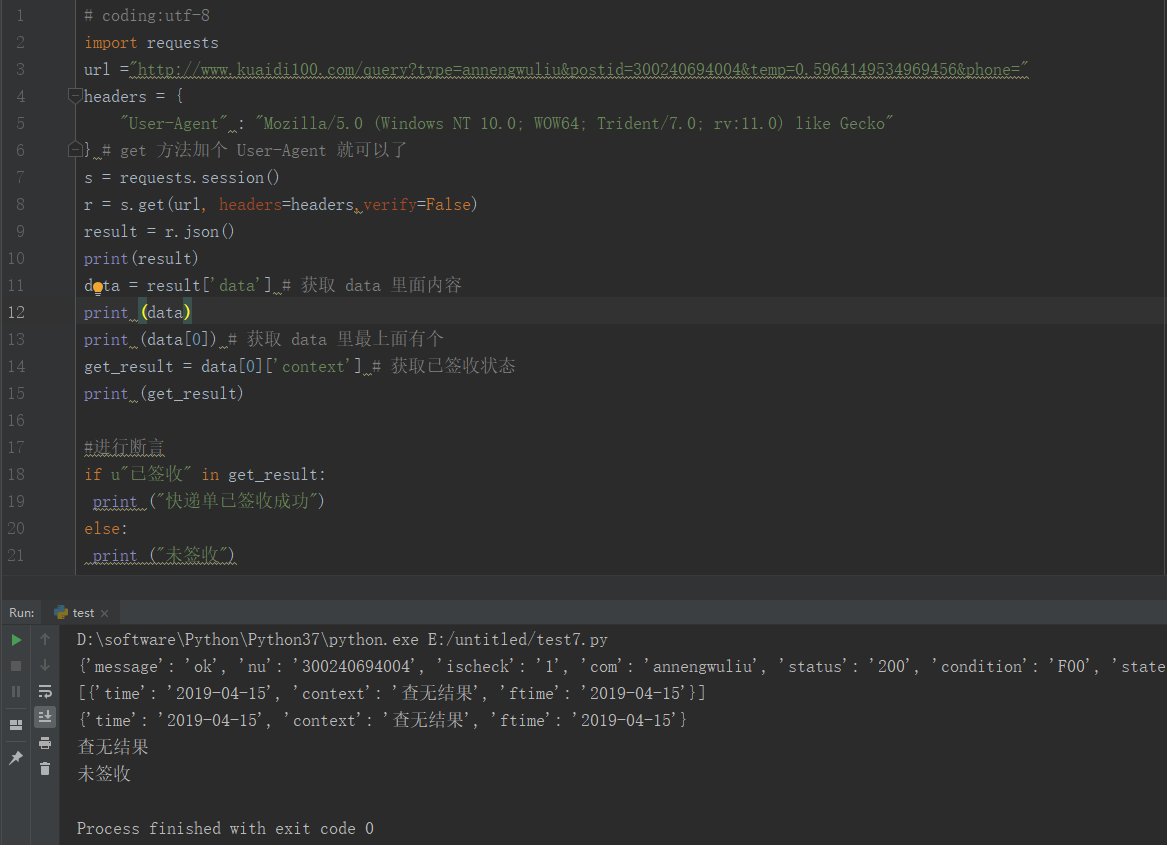
参考代码
1 # coding:utf-82 import requests3 url ="http://www.kuaidi100.com/query?type=annengwuliu&postid=300240694004&temp=0.5964149534969456&phone="4 headers = {5 "User-Agent" : "Mozilla/5.0 (Windows NT 10.0; WOW64; Trident/7.0; rv:11.0) like Gecko"6 } # get 方法加个 User-Agent 就可以了7 s = requests.session()8 r = s.get(url, headers=headers,verify=False)9 result = r.json()
10 print(result)
11 data = result['data'] # 获取 data 里面内容
12 print (data)
13 print (data[0]) # 获取 data 里最上面有个
14 get_result = data[0]['context'] # 获取已签收状态
15 print (get_result)
16
17 #进行断言
18 if u"已签收" in get_result:
19 print ("快递单已签收成功")
20 else:
21 print ("未签收")
小结
各位小伙伴,看到了,断言就是这么简单,其实和你写的测试用例差不多,将预期与实际结果进行对比,只不过是用代码体现出来。
最后感谢每一个认真阅读我文章的人,看着粉丝一路的上涨和关注,礼尚往来总是要有的,虽然不是什么很值钱的东西,如果你用得到的话可以直接拿走!
软件测试面试文档
我们学习必然是为了找到高薪的工作,下面这些面试题是来自阿里、腾讯、字节等一线互联网大厂最新的面试资料,并且有字节大佬给出了权威的解答,刷完这一套面试资料相信大家都能找到满意的工作。

相关文章:

Python接口自动化 —— Json 数据处理实战(详解)
简介 上一篇说了关于json数据处理,是为了断言方便,这篇就带各位小伙伴实战一下。首先捋一下思路,然后根据思路一步一步的去实现和实战,不要一开始就盲目的动手和无头苍蝇一样到处乱撞,撞得头破血流后而放弃了。不仅什么…...
微信页面公众号页面 安全键盘收起后页面空白
微信浏览器打开H5页面和公众号页面,输入密码时调起安全键盘,键盘收起后 键盘下方页面留白 解决办法: 1、(简单)只有在调起安全键盘(输入密码)的时候会出现这种情况,将input属性改为n…...

数据结构 - 二叉树
递归实现前中后序遍历 #include<stdio.h> #include<stdlib.h>#define TElemType inttypedef struct BiTNode{TElemType data;struct BiTNode *lchild,*rchild; }BiTNode,*BiTree; BiTNode root;void visit(TElemType& e){printf("%d",e); }void Pre…...

【Overload游戏引擎细节分析】从视图投影矩阵提取视锥体及overload对视锥体的封装
overoad代码中包含一段有意思的代码,可以从视图投影矩阵逆推出摄像机的视锥体,本文来分析一下原理 一、平面的方程 视锥体是用平面来表示的,所以先看看平面的数学表达。 平面方程可以由其法线N(A, B, C)和一个点Q(x0,…...

Linux 安全 - LSM hook点
文章目录 一、LSM file system hooks1.1 LSM super_block hooks1.2 LSM file hooks1.3 LSM inode hooks 二、LSM Task hooks三、LSM IPC hooks四、LSM Network hooks五、LSM Module & System hooks 一、LSM file system hooks 在VFS(虚拟文件系统)层…...

【iOS逆向与安全】越狱检测与过检测附ida伪代码
首先在网上查找一些检测代码 放入项目运行,用 ida 打开后 F5 得到下面的 __int64 __usercall sub_10001B3F0<X0>(__int64 a1, __int64 a2, __int64 a3, __int64 a4, __int64 a5, __int64 a6, __int64 a7, __int64 a8, __int64 a9, __int64 a10, __int64 a11…...

Android Studio gradle手动下载配置
项目同步时,有时候会遇到Android Studio第一步下载gradle就是连接失败的问题。 这种情况,我们可以手动去gradle官网下载好gradle文件,放置在Android Studio的缓存目录下,这样AS在同步代码时就会自动解压下载好的文件。 步骤如下&…...
)
ChatGPT Prompting开发实战(十三)
一. 如何评估prompts是否包含有害内容 用户在与ChatGPT交互时提供的prompts可能会包括有害内容,这时可以通过调用OpenAI提供的API来进行判断,接下来给出示例,通过调用模型“gpt-3.5-turbo”来演示这个过程。 prompt示例如下&…...
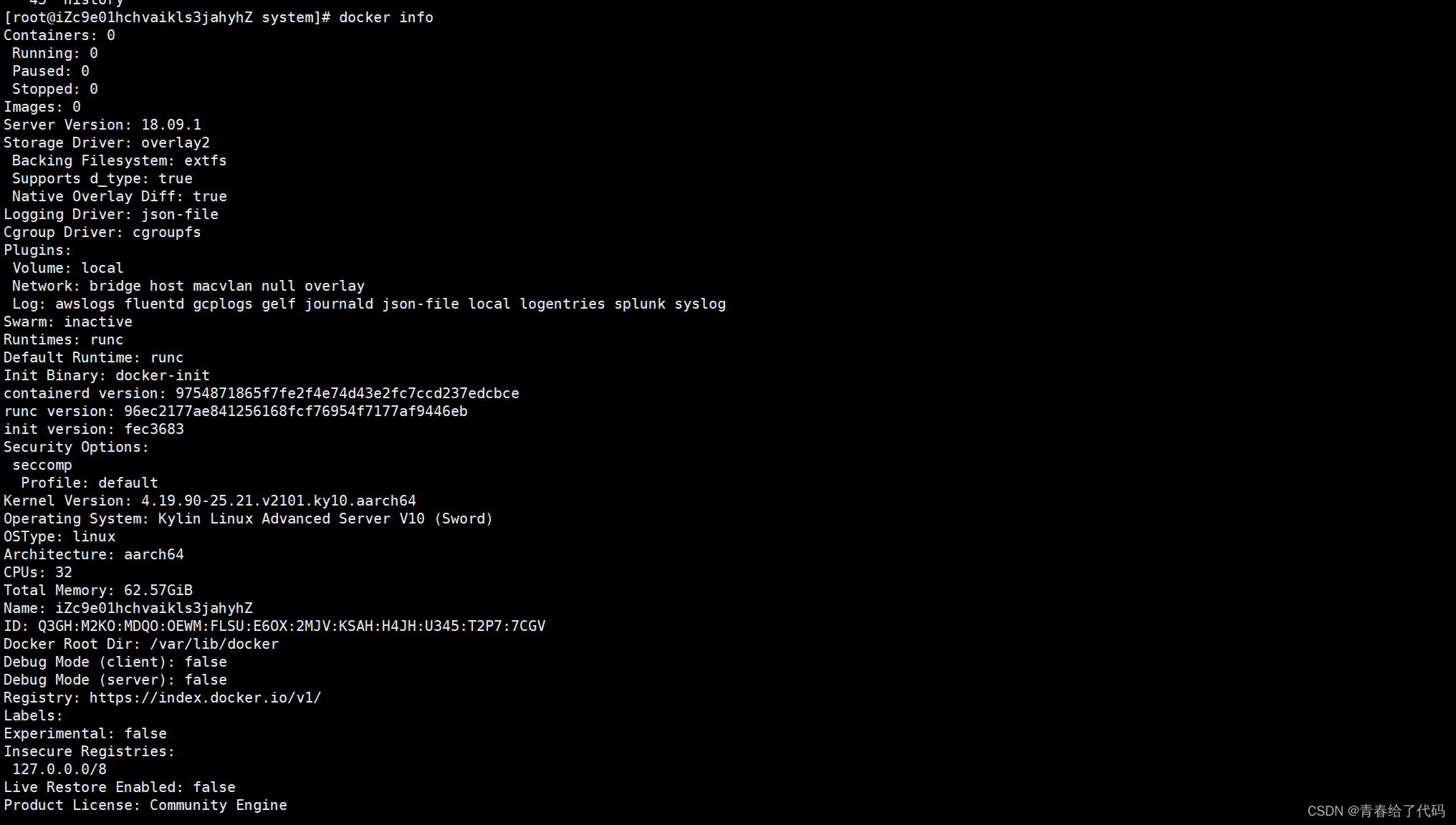
银河麒麟 ARM 架构 离线安装Docker
1. 下载对应的安装包 进入此地址下载对应的docker 离线安装包 下载地址 将文件上传到服务器 解压此文件 tar zxf docker-18.09.1.tgz将 docker 相关命令拷贝到 /usr/bin,方便直接运行命令 cp docker/* /usr/bin/启动Docker守护程序 dockerd &验证是否安装成…...

虹科科技 | 探索CAN通信世界:PCAN-Explorer 6软件的功能与应用
CAN(Controller Area Network)总线是一种广泛应用于汽车和工业领域的通信协议,用于实时数据传输和设备之间的通信。而虹科的PCAN-Explorer 6软件是一款功能强大的CAN总线分析工具,为开发人员提供了丰富的功能和灵活性。本文将重点…...

SELECT COUNT(*)会不会导致全表扫描引起慢查询
SELECT COUNT(*)会不会导致全表扫描引起慢查询呢? SELECT COUNT(*) FROM SomeTable 网上有一种说法,针对无 where_clause 的 COUNT(*),MySQL 是有优化的,优化器会选择成本最小的辅助索引查询计数,其实反而性能最高&…...

英国物联网初创公司【FourJaw】完成180万英镑融资
来源:猛兽财经 作者:猛兽财经 猛兽财经获悉,总部位于英国谢菲尔德的物联网初创公司【FourJaw】今日宣布已完成180万英镑融资。 本轮融资完成后,FourJaw的总融资金额已达400万英镑,本轮融资的投资机构包括:…...

许战海战略文库|无增长则衰亡:中小型制造企业增长困境
竞争环境不是匀速变化,而是加速变化。企业的衰退与进化、兴衰更迭在不断发生,这成为一种不可避免的现实。事实上,在产业链竞争中增长困境不分企业大小,而是一种普遍存在的问题,许多收入在1亿至10亿美元间的制造企业也同…...

广州华锐互动:候车室智能数字孪生系统实现交通信息可视化
随着科技的不断发展,数字化技术在各个领域得到了广泛的应用。智慧车站作为一种新型的交通服务模式,通过运用先进的数字化技术,为乘客提供了更加便捷、舒适的出行体验。 将智慧车站与数字孪生大屏结合,可以将实际现实世界的实体车站…...
智慧工地:助力数字建造、智慧建造、安全建造、绿色建造
智慧工地管理系统融合计算机技术、物联网、视频处理、大数据、云计算等,为工程项目管理提供先进的技术手段,构建施工现场智能监控系统,有效弥补传统监理中的缺陷,对人、机、料、法、环境的管理由原来的被动监督变成全方位的主动管…...
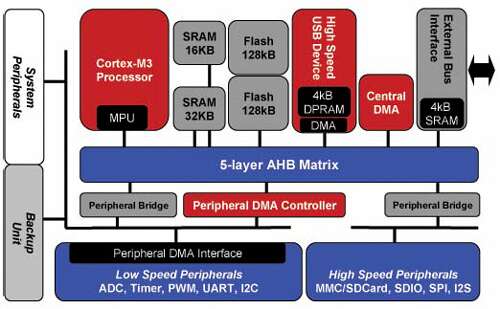
增强基于Cortex-M3的MCU以处理480 Mbps高速USB
通用串行总线(USB)完全取代了PC上的UART,PS2和IEEE-1284并行接口,现在已在嵌入式开发应用程序中得到广泛认可。嵌入式开发系统使用的大多数I / O设备(键盘,扫描仪,鼠标)都是基于USB的…...
山海鲸汽车需求调研系统:智慧决策的关键一步
随着社会的发展和科技的进步,汽车行业也迎来了新的挑战和机遇。如何更好地满足用户需求、提高产品竞争力成为了汽车制造商们关注的焦点。在这个背景下,山海鲸汽车需求调研互动系统应运而生,为汽车行业赋予了智慧决策的力量。 智慧决策的核心&…...

视频缩放的概念整理-步长数组
最近在读ffmpeg的代码时候,这个接口不是很能看懂int sws_scale(struct SwsContext *c, const uint8_t *const srcSlice[], const int srcStride[], int srcSliceY, int srcSliceH, uint8_t *const dst[], const int dstStride[]); 多方请教后,记录结果如…...
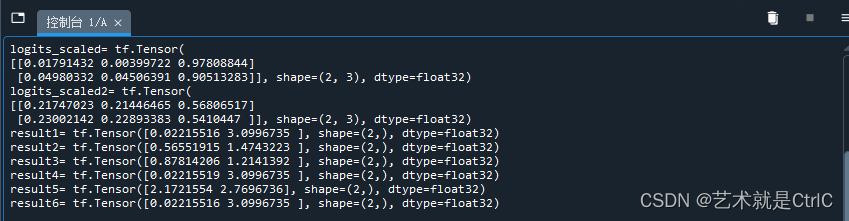
TensorFlow入门(二十一、softmax算法与损失函数)
在实际使用softmax计算loss时,有一些关键地方与具体用法需要注意: 交叉熵是十分常用的,且在TensorFlow中被封装成了多个版本。多版本中,有的公式里直接带了交叉熵,有的需要自己单独手写公式求出。如果区分不清楚,在构建模型时,一旦出现问题将很难分析是模型的问题还是交叉熵的使…...

UDP通信:快速入门
UDP协议通信模型演示 UDP API DatagramPacket:数据包对象(韭菜盘子) public DatagramPacket(byte[] buf, int length, InetAddress address, int port)创建发送端数据包对象 buf:要发送的内容,字节数组 length&…...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...

HDFS分布式存储 zookeeper
hadoop介绍 狭义上hadoop是指apache的一款开源软件 用java语言实现开源框架,允许使用简单的变成模型跨计算机对大型集群进行分布式处理(1.海量的数据存储 2.海量数据的计算)Hadoop核心组件 hdfs(分布式文件存储系统)&a…...

面向无人机海岸带生态系统监测的语义分割基准数据集
描述:海岸带生态系统的监测是维护生态平衡和可持续发展的重要任务。语义分割技术在遥感影像中的应用为海岸带生态系统的精准监测提供了有效手段。然而,目前该领域仍面临一个挑战,即缺乏公开的专门面向海岸带生态系统的语义分割基准数据集。受…...

【Android】Android 开发 ADB 常用指令
查看当前连接的设备 adb devices 连接设备 adb connect 设备IP 断开已连接的设备 adb disconnect 设备IP 安装应用 adb install 安装包的路径 卸载应用 adb uninstall 应用包名 查看已安装的应用包名 adb shell pm list packages 查看已安装的第三方应用包名 adb shell pm list…...

FFmpeg:Windows系统小白安装及其使用
一、安装 1.访问官网 Download FFmpeg 2.点击版本目录 3.选择版本点击安装 注意这里选择的是【release buids】,注意左上角标题 例如我安装在目录 F:\FFmpeg 4.解压 5.添加环境变量 把你解压后的bin目录(即exe所在文件夹)加入系统变量…...

MySQL 部分重点知识篇
一、数据库对象 1. 主键 定义 :主键是用于唯一标识表中每一行记录的字段或字段组合。它具有唯一性和非空性特点。 作用 :确保数据的完整性,便于数据的查询和管理。 示例 :在学生信息表中,学号可以作为主键ÿ…...
