【Overload游戏引擎细节分析】从视图投影矩阵提取视锥体及overload对视锥体的封装
overoad代码中包含一段有意思的代码,可以从视图投影矩阵逆推出摄像机的视锥体,本文来分析一下原理
一、平面的方程
视锥体是用平面来表示的,所以先看看平面的数学表达。
平面方程可以由其法线N=(A, B, C)和一个点Q=(x0,y0,z0)定义,其形式为:
A ( x − x 0 ) + B ( y − y 0 ) + C ( z − z 0 ) = 0 A(x-x_{0})+B(y-y_{0})+C(z-z_{0})=0 A(x−x0)+B(y−y0)+C(z−z0)=0 整理变为: A x + B y + C z + D = 0 Ax+By+Cz+D=0 Ax+By+Cz+D=0, 其中 D = − A x 0 − B y 0 − C z 0 D=−Ax_{0}−By_{0}−Cz_{0} D=−Ax0−By0−Cz0
方程进一步可以将方程归一化:
A A 2 + B 2 + C 2 x + B A 2 + B 2 + C 2 y + C A 2 + B 2 + C 2 z + D A 2 + B 2 + C 2 = 0 \frac{A}{\sqrt{A^{2}+B^{2}+C^{2} } } x + \frac{B}{\sqrt{A^{2}+B^{2}+C^{2} } }y+\frac{C}{\sqrt{A^{2}+B^{2}+C^{2} } }z+\frac{D}{\sqrt{A^{2}+B^{2}+C^{2} } } = 0 A2+B2+C2Ax+A2+B2+C2By+A2+B2+C2Cz+A2+B2+C2D=0 写成通用格式 a x + b y + c z + d = 0 ax+by+cz+d=0 ax+by+cz+d=0
那么点 p = ( x 1 , y 1 , z 1 ) p=(x_{1}, y_{1}, z_{1}) p=(x1,y1,z1)到平面的距离为:
D = a x 1 + b y 1 + c z 1 + d D=ax_{1}+by_{1}+cz_{1}+d D=ax1+by1+cz1+d
一个平面会将空间分成两个半空间(halfspace),进一步法线的朝向的空间称为正半空间(positive halfspace),法线背离的空间称为反半空间(negative halfspace)。根据D的符号可以判断点的相对位置:
- D < 0, 点位于反半空间
- D = 0, 点位于平面上
- D > 0, 点位于正半空间
这种特性可用于判断点是否在视锥体内部。
二、OpenGL视锥体
视锥体是摄像机能看到的区域,只有在视锥体内的物体才能被看到。其由近平面near、远平面far与周围四个面top、bottom、left、right组成,形成一个平截头体区域。

不过在构建视锥体时一般不直接输入6个平面的方程,常用另外一组更直观易懂的参数:
- fov – 视锥体的垂直张角
- Near – 视锥体的近平面距离
- Far – 视锥体的远平面距离
- aspect – 相机视口的长宽比
具体含义建下图:

三、Overload对视锥体的封装
Overload对视锥体的封装在文件Frustum.h、Frustum.cpp中。先看其定义:
class Frustum
{
public:/*** 根据视图投影矩阵提取视锥体* @param p_viewProjection*/ void CalculateFrustum(const OvMaths::FMatrix4& _viewProjection);/*** 判断点是不是在视锥体内* @param p_x* @param p_y* @param p_z*/bool PointInFrustum(float p_x, float p_y, float _z) const;/*** 判断球是不是在视锥体内* @param p_x* @param p_y* @param p_z* @param p_radius*/bool SphereInFrustum(float p_x, float p_y, loat p_z, float p_radius) const;/*** 判断立方体是不是在视锥体内* @param p_x* @param p_y* @param p_z* @param p_size*/bool CubeInFrustum(float p_x, float p_y, float _z, float p_size) const;/*** 判断包围球是不是在视锥体内* @param p_boundingSphere* @param p_transform*/bool BoundingSphereInFrustum(const vRendering::Geometry::BoundingSphere& _boundingSphere, const OvMaths::FTransform& _transform) const;/*** 返回近平面*/std::array<float, 4> GetNearPlane() const;/*** 返回远平面*/std::array<float, 4> GetFarPlane() const;
private:float m_frustum[6][4]; // 6个平面的方程参数
};
m_frustum保存着6个平面的方程参数,为了提升操作便利性,其定义了两个枚举作为索引:
enum FrustumSide
{RIGHT = 0, // The RIGHT side of the frustumLEFT = 1, // The LEFT side of the frustumBOTTOM = 2, // The BOTTOM side of the frustumTOP = 3, // The TOP side of the frustumBACK = 4, // The BACK side of the frustumFRONT = 5 // The FRONT side of the frustum
};// 平面方程的参数索引
enum PlaneData
{A = 0, // The X value of the plane's normalB = 1, // The Y value of the plane's normalC = 2, // The Z value of the plane's normalD = 3 // The distance the plane is from the origin
};
函数的具体实现在文件Frustum.cpp中,我们先看最基础的判断点是否在视锥体内:
bool OvRendering::Data::Frustum::PointInFrustum(float x, float y, float z) const
{for (int i = 0; i < 6; i++){if (m_frustum[i][A] * x + m_frustum[i][B] * y + m_frustum[i][C] * z + m_frustum[i][D] <= 0){return false;}}return true;
}
定义视锥体的面法线都是朝外的,如果点在视锥体内,点到6个面的距离必须全部小于0。进一步判断球体是否完全在视锥体内,距离必须小于半径的负数。
最后分析一下CalculateFrustum,它是根据一个视图投影矩阵反向构建一个视锥体,具体公式怎么来的可以参考这篇文章,里面将的特别详细:
Fast Extraction of Viewing Frustum Planes from the World View-Projection Matrix
其本身的代码没啥好说的,无非就是公式的翻译。
相关文章:

【Overload游戏引擎细节分析】从视图投影矩阵提取视锥体及overload对视锥体的封装
overoad代码中包含一段有意思的代码,可以从视图投影矩阵逆推出摄像机的视锥体,本文来分析一下原理 一、平面的方程 视锥体是用平面来表示的,所以先看看平面的数学表达。 平面方程可以由其法线N(A, B, C)和一个点Q(x0,…...

Linux 安全 - LSM hook点
文章目录 一、LSM file system hooks1.1 LSM super_block hooks1.2 LSM file hooks1.3 LSM inode hooks 二、LSM Task hooks三、LSM IPC hooks四、LSM Network hooks五、LSM Module & System hooks 一、LSM file system hooks 在VFS(虚拟文件系统)层…...

【iOS逆向与安全】越狱检测与过检测附ida伪代码
首先在网上查找一些检测代码 放入项目运行,用 ida 打开后 F5 得到下面的 __int64 __usercall sub_10001B3F0<X0>(__int64 a1, __int64 a2, __int64 a3, __int64 a4, __int64 a5, __int64 a6, __int64 a7, __int64 a8, __int64 a9, __int64 a10, __int64 a11…...

Android Studio gradle手动下载配置
项目同步时,有时候会遇到Android Studio第一步下载gradle就是连接失败的问题。 这种情况,我们可以手动去gradle官网下载好gradle文件,放置在Android Studio的缓存目录下,这样AS在同步代码时就会自动解压下载好的文件。 步骤如下&…...
)
ChatGPT Prompting开发实战(十三)
一. 如何评估prompts是否包含有害内容 用户在与ChatGPT交互时提供的prompts可能会包括有害内容,这时可以通过调用OpenAI提供的API来进行判断,接下来给出示例,通过调用模型“gpt-3.5-turbo”来演示这个过程。 prompt示例如下&…...
银河麒麟 ARM 架构 离线安装Docker
1. 下载对应的安装包 进入此地址下载对应的docker 离线安装包 下载地址 将文件上传到服务器 解压此文件 tar zxf docker-18.09.1.tgz将 docker 相关命令拷贝到 /usr/bin,方便直接运行命令 cp docker/* /usr/bin/启动Docker守护程序 dockerd &验证是否安装成…...

虹科科技 | 探索CAN通信世界:PCAN-Explorer 6软件的功能与应用
CAN(Controller Area Network)总线是一种广泛应用于汽车和工业领域的通信协议,用于实时数据传输和设备之间的通信。而虹科的PCAN-Explorer 6软件是一款功能强大的CAN总线分析工具,为开发人员提供了丰富的功能和灵活性。本文将重点…...

SELECT COUNT(*)会不会导致全表扫描引起慢查询
SELECT COUNT(*)会不会导致全表扫描引起慢查询呢? SELECT COUNT(*) FROM SomeTable 网上有一种说法,针对无 where_clause 的 COUNT(*),MySQL 是有优化的,优化器会选择成本最小的辅助索引查询计数,其实反而性能最高&…...

英国物联网初创公司【FourJaw】完成180万英镑融资
来源:猛兽财经 作者:猛兽财经 猛兽财经获悉,总部位于英国谢菲尔德的物联网初创公司【FourJaw】今日宣布已完成180万英镑融资。 本轮融资完成后,FourJaw的总融资金额已达400万英镑,本轮融资的投资机构包括:…...

许战海战略文库|无增长则衰亡:中小型制造企业增长困境
竞争环境不是匀速变化,而是加速变化。企业的衰退与进化、兴衰更迭在不断发生,这成为一种不可避免的现实。事实上,在产业链竞争中增长困境不分企业大小,而是一种普遍存在的问题,许多收入在1亿至10亿美元间的制造企业也同…...

广州华锐互动:候车室智能数字孪生系统实现交通信息可视化
随着科技的不断发展,数字化技术在各个领域得到了广泛的应用。智慧车站作为一种新型的交通服务模式,通过运用先进的数字化技术,为乘客提供了更加便捷、舒适的出行体验。 将智慧车站与数字孪生大屏结合,可以将实际现实世界的实体车站…...
智慧工地:助力数字建造、智慧建造、安全建造、绿色建造
智慧工地管理系统融合计算机技术、物联网、视频处理、大数据、云计算等,为工程项目管理提供先进的技术手段,构建施工现场智能监控系统,有效弥补传统监理中的缺陷,对人、机、料、法、环境的管理由原来的被动监督变成全方位的主动管…...
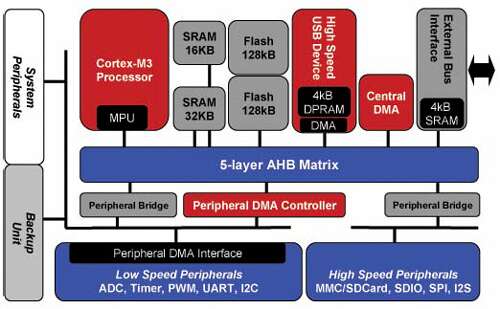
增强基于Cortex-M3的MCU以处理480 Mbps高速USB
通用串行总线(USB)完全取代了PC上的UART,PS2和IEEE-1284并行接口,现在已在嵌入式开发应用程序中得到广泛认可。嵌入式开发系统使用的大多数I / O设备(键盘,扫描仪,鼠标)都是基于USB的…...
山海鲸汽车需求调研系统:智慧决策的关键一步
随着社会的发展和科技的进步,汽车行业也迎来了新的挑战和机遇。如何更好地满足用户需求、提高产品竞争力成为了汽车制造商们关注的焦点。在这个背景下,山海鲸汽车需求调研互动系统应运而生,为汽车行业赋予了智慧决策的力量。 智慧决策的核心&…...

视频缩放的概念整理-步长数组
最近在读ffmpeg的代码时候,这个接口不是很能看懂int sws_scale(struct SwsContext *c, const uint8_t *const srcSlice[], const int srcStride[], int srcSliceY, int srcSliceH, uint8_t *const dst[], const int dstStride[]); 多方请教后,记录结果如…...
TensorFlow入门(二十一、softmax算法与损失函数)
在实际使用softmax计算loss时,有一些关键地方与具体用法需要注意: 交叉熵是十分常用的,且在TensorFlow中被封装成了多个版本。多版本中,有的公式里直接带了交叉熵,有的需要自己单独手写公式求出。如果区分不清楚,在构建模型时,一旦出现问题将很难分析是模型的问题还是交叉熵的使…...

UDP通信:快速入门
UDP协议通信模型演示 UDP API DatagramPacket:数据包对象(韭菜盘子) public DatagramPacket(byte[] buf, int length, InetAddress address, int port)创建发送端数据包对象 buf:要发送的内容,字节数组 length&…...

修炼k8s+flink+hdfs+dlink(四:k8s(一)概念)
一:概念 1. 概述 1.1 kubernetes对象. k8s对象包含俩个嵌套对象字段。 spec(规约):期望状态 status(状态):当前状态 当创建对象的时候,会按照spec的状态进行创建,如果…...

redis与 缓存击穿、缓存穿透、缓存雪崩
什么是缓存击穿、缓存穿透、缓存雪崩 缓存击穿、缓存穿透和缓存雪崩是与缓存相关的三种常见问题,它们可以在高并发的应用中导致性能问题。以下是它们的解释: 缓存击穿(Cache Miss) 缓存击穿指的是在高并发情况下,有大…...

印度网络安全:威胁与应对
随着今年过半,我们需要评估并了解不断崛起的网络威胁复杂性,这些威胁正在改变我们的数字景观。 从破坏性的网络钓鱼攻击到利用人工智能的威胁,印度的网络犯罪正在升级。然而,在高调的数据泄露事件风暴中,我们看到了政…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

JVM垃圾回收机制全解析
Java虚拟机(JVM)中的垃圾收集器(Garbage Collector,简称GC)是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象,从而释放内存空间,避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...
:爬虫完整流程)
Python爬虫(二):爬虫完整流程
爬虫完整流程详解(7大核心步骤实战技巧) 一、爬虫完整工作流程 以下是爬虫开发的完整流程,我将结合具体技术点和实战经验展开说明: 1. 目标分析与前期准备 网站技术分析: 使用浏览器开发者工具(F12&…...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...

高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数
高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数 在软件开发中,单例模式(Singleton Pattern)是一种常见的设计模式,确保一个类仅有一个实例,并提供一个全局访问点。在多线程环境下,实现单例模式时需要注意线程安全问题,以防止多个线程同时创建实例,导致…...
的使用)
Go 并发编程基础:通道(Channel)的使用
在 Go 中,Channel 是 Goroutine 之间通信的核心机制。它提供了一个线程安全的通信方式,用于在多个 Goroutine 之间传递数据,从而实现高效的并发编程。 本章将介绍 Channel 的基本概念、用法、缓冲、关闭机制以及 select 的使用。 一、Channel…...

Oracle11g安装包
Oracle 11g安装包 适用于windows系统,64位 下载路径 oracle 11g 安装包...
