数学建模——人工神经网络模型
一、人工神经网络简介
1、神经网络起源与应用
1943年心理学家McCulloch和数学家Pitts提出神经元生物数学模型(M-P模型),后来人工神经网络(Artifical Neural Network,ANN)是在生物神经网络(Biological Neural Network,BNN)基础上发展起来的,是对人脑的某种抽象、简化和模拟,是模拟人的智能的一种途径。
神经元是神经网络的基本处理单元,一个简化的神经元是多输入、单输出的非线性元件,大量的神经元互联而成的神经网络(非线性元件),在人工智能和机器自学习、自组织、联想以及容错方面具有强大的能力。
2、人工神经元的工作原理
大脑的神经细胞由细胞体(soma)、一些树突(dendrite)和一根可以很长的轴突(Axon)组成,树突由细胞体的各个方向长出,本身可有分支,是用来接受信号的,轴突也有许多分支,通过分支末梢(terminal)和其它细胞的树突接触,形成突触,把产生的信号传送给其它细胞,如图(1)所示。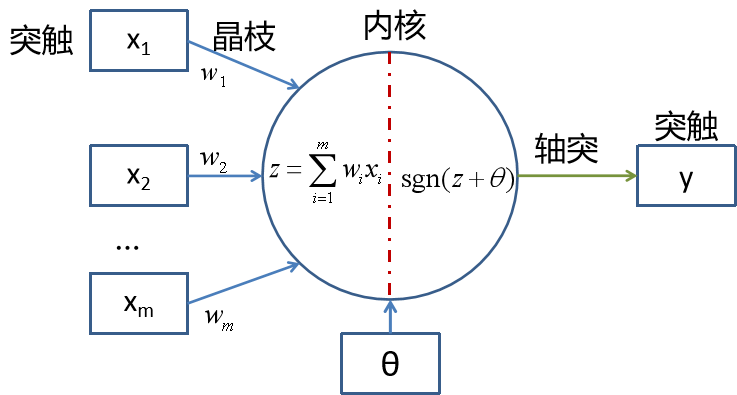
图(1) McCulloch-Pitts网络
大脑的神经元细胞只有两种状态:兴奋和压抑。神经细胞把所有从树突上突触进来的信号进行相加,如果全部信号超过某个阈值,就会激发细胞进入兴奋状态,就会有信号通过轴突发送信号给其它细胞。如果信号没有超过阈值,细胞就不会兴奋。
模拟大脑的人工神经网络是采用神经元组成的,神经元是人工神经网络的基本处理单元,它一般是一个多输入/多输出的非线性元件。神经元输出受到输入信号和内部其它因素的影响,所以人工神经元的建模中,常常还有一个额外的输入信号,称为偏差(bais),有时也称为阀值或限值。
人工神经网络模拟生物神经元的一阶特性,人工神经元有n个输入,即输入为X=(x1,x2,…,xn),连接权为W=(w1,w2,…,wn)T,神经元输出为 采用向量的形式,即Net=X·W-θ.
采用向量的形式,即Net=X·W-θ.
3、神经网络结构
三层前馈神经网络的构造由三层排列,分别是输入层、隐含层(中间层)和输出层。每一层的神经元接受来自前一层神经元的输出作为输入,后面层对前面的层没有反馈。感知器网络和BP网络均属前馈网络。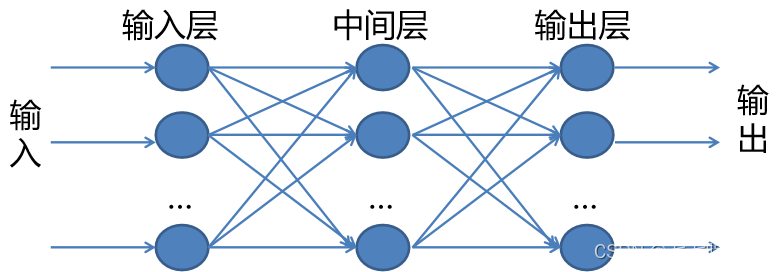
三层前向神经网络结构
4、神经网络常用激励函数
激励函数,又称激活函数或传递函数,通常有三种
(1)阀值型
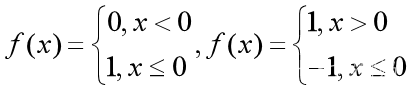 这里函数一般用在简单的分类模型中。
这里函数一般用在简单的分类模型中。
(2)线性型
f(x)=x 一般只用在输入神经元和输出神经元。
(3)S型
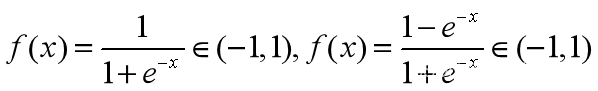
常用于隐含层,第一个为logsig()函数,第二个为logtan()函数。都是光滑函数,且第一个函数满足![]()
二、常见神经网络理论
1、BP神经网络
BP(Back propagation)神经网络,又称前向反馈神经网络,主要是网络训练中,调整权值和阀值的训练算法时反向传播算法(即BP学习算法),也是神经网络的精华和完美的内容。 BP神经网络是一种有三层或三层以上的神经网络,概括输入层、中间层(隐含层)和输出层,上下层之间全连接,同层之间神经元无连接。
当一对学习样本提供给输入层神经元后,神经元的激活值(该层神经元的输出值)从输入层经过各隐含层神经元向输出层传播,在输出层获得网络的输入响应,然后按照减少网络输出与实际样本样本之间误差的反向,从输出层反向经过隐含层回到输入层,从而逐步修正连接权值,这种算法称为“误差反向传播算法”,即BP算法。随着这种误差逆向传播修正的反复进行,网络对输入模式相应的正确率不断上升,BP算法的核心是“负梯度下降”理论,即BP神经网络的误差调整总是沿着误差下降最快的方向进行。
为了更好地理解BP神经网络,我们来看一个简单的例子:假设我们要训练一个网络来判断一张图片中的数字是1还是0。
首先,我们将每个像素点作为输入层的一个神经元,并将它们与隐藏层的每个神经元连接起来。隐藏层可以有多个神经元,影响网络的复杂度和表示能力。
然后,我们将隐藏层的每个神经元与输出层的两个神经元(代表数字1和0)相连。
在训练过程中,我们将输入一张图片,网络将对其进行前向传播,即通过网络计算出预测结果。然后,我们将预测结果与实际标签进行比较,并计算出损失函数(通常使用交叉熵损失)来衡量预测的错误程度。
接下来,反向传播算法将根据损失函数的梯度来调整每个连接的权重,以减小损失函数的值。这个过程会逐渐优化网络的预测能力,使得网络能够更准确地判断输入图片中的数字是1还是0。
通过不断迭代上述步骤,网络学习到的权重参数将使其在对新的图片进行数字分类时具有较好的准确性。
2、径向基网络
RBF(Radical Basis Function)神经网络。生物学中,中枢神经元的感受视野是指能影响某一神经元反应的视网膜或视野的区域。视网膜上的感受器(杆体细胞和锥体细胞)通过接受光并将它转换为神经输出信号,从而不同程度地激活众多神经节细胞、外膝状体细胞以及视觉皮层中的神经细胞。RBF神经网络是模拟视网膜的感受功能而产生的,其基本特征是:
(1)距离感受视野中心的越近,视神经元越兴奋,距离感受中心越远,视神经元响应越消极; (2)视神经元的激活区域呈现径向对称。
综上所述,隐含层的视神经元的刺激函数常用高斯函数,即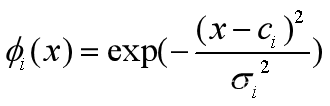 (i为隐含层第i神经元)
(i为隐含层第i神经元)
而输入和输出则采用线性激励函数。其中,x为输入样本,ci为感受视野中心,σ为宽度,exp( )为隐含层输出。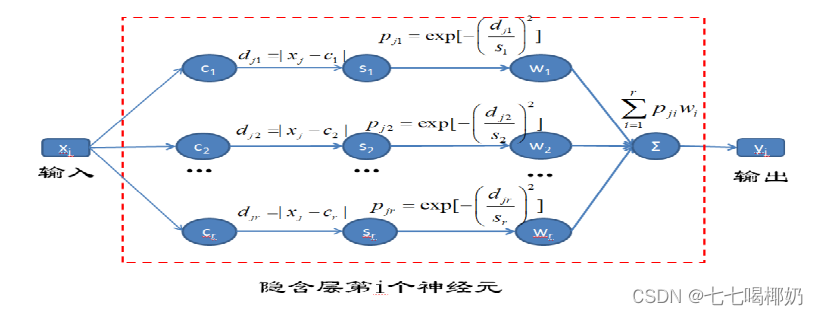
RBF学习方法
- 聚类方法 : 首选k聚类,即先用k—means方法确定网络数据的中心,然后根据各数据与中心的距离,确定隐含层神经元函数的宽度。
- 梯度训练法 :根据能量函数使用负梯度训练原理自行调节各神经元的数据中心、宽度、权值。
- 正交最小二乘(OLS)训练方法:依据能量的贡献,使各隐含层神经元的基函数之间趋于正交,从而使基函数之间没有信息冗余和性能相互嵌套。
相关文章:

数学建模——人工神经网络模型
一、人工神经网络简介 1、神经网络起源与应用 1943年心理学家McCulloch和数学家Pitts提出神经元生物数学模型(M-P模型),后来人工神经网络(Artifical Neural Network,ANN)是在生物神经网络(Biological Neural Network,BNN)基础上发展起来的&a…...

java合成多个pdf为一个pdf
pom文件 <dependency><groupId>com.lowagie</groupId><artifactId>itext</artifactId><version>2.1.7</version></dependency>主文件 import com.lowagie.text.Document; import com.lowagie.text.pdf.PdfCopy; import com.lo…...
“高级Vue状态管理 - Vuex的魅力与应用“
目录 引言1. Vuex的简介1.1 什么是Vuex?1.2 Vuex的核心概念 2. Vuex的值获取与改变(综合案例)3. Vuex的异步请求总结 引言 在现代Web开发中,前端应用变得越来越复杂。随着应用规模的扩大和数据流的复杂性增加,有效地管理应用的状态成为了一项…...

Vue整合
基础配置: 1.创建:cmd 中 输入 create vue vue_name 启动命令:npm run serve 2.当node_modules(依赖)丢失时通过 npm install 下载 【根据:package-lock.json下载】 3.下载路由 npm i vue-router3.5.2 -S main.js导入 // np…...

探秘PMP和六西格玛的不同:哪一个能为你的职业生涯加分?
今天,我们将带你深入了解一项相对冷门但价值不菲的证书——六西格玛黑带。 可能你曾听说过PMP,但相比之下,六西格玛黑带的资源分享似乎较少,考试内容却更为广泛深入。这里,让我为你详细解析这一考试,带你进…...
-hive分区表与分桶表)
大数据学习(3)-hive分区表与分桶表
&&大数据学习&& 🔥系列专栏: 👑哲学语录: 承认自己的无知,乃是开启智慧的大门 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言📝支持一下博>主哦&#x…...

JS 原生实现触底加载
创建一个容器来存储列表项。 监听滚动事件,当滚动接近底部时触发加载更多操作。 加载更多数据后,将新数据附加到容器中。 以下是一个简单的示例: <!DOCTYPE html> <html><head><style>#scroll-container {heigh…...

结构体,位段!
目录 1.什么是位段? 别急!在下面第二点我和大家介绍。 2.位段的内存怎么分配? 还有一种情况就是两种类型夹杂在一起的位段 3.位段的跨平台问题 4.位段能干嘛?(应用) 5.位段的注意事项 1.什么是位段&…...

当10年程序员是什么体验?存款几位数?
最近网上一个话题吸引了许多人的讨论,当10年程序员,是一种什么体验? 都说程序员的高收入和工作年限应该成正比,真的是这样吗?工作10年的程序员,工资应该是什么水平?不少网友纷纷“现身说法”..…...
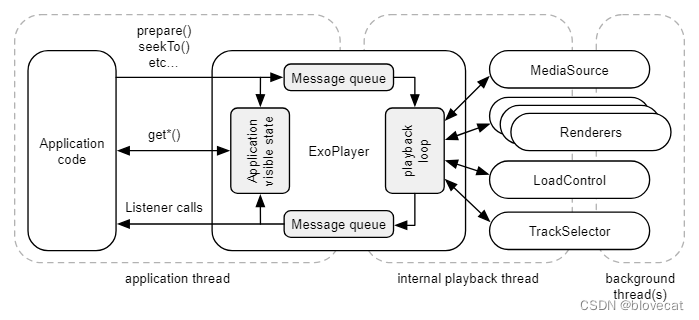
ExoPlayer架构详解与源码分析(4)——整体架构
系列文章目录 ExoPlayer架构详解与源码分析(1)——前言 ExoPlayer架构详解与源码分析(2)——Player ExoPlayer架构详解与源码分析(3)——Timeline ExoPlayer架构详解与源码分析(4)—…...

rust文件读写
std::fs模块提供了结构体File,它表示一个文件。 一、打开文件 结构体File提供了open()函数 open()以只读模式打开文件,如果文件不存在,则会抛出一个错误。如果文件不可读,那么也会抛出一个错误。 范例 fn main() {let file s…...

腾讯云我的世界mc服务器配置选择和价格表
开Minecraft我的世界服务器配置怎么选择?10人以内玩2核4G就够用了,开我的世界服务器选择轻量应用服务器就够了,腾讯云轻量应用服务器2核2G3M带宽轻量服务器一年95元,活动:txyfwq.com/go/tencent 轻量CPU采用至强白金处…...

基于安卓android微信小程序的旅游系统
项目介绍 随着人民生活水平的提高,旅游业已经越来越大众化,而旅游业的核心是信息,不论是对旅游管理部门、对旅游企业,或是对旅游者而言,有效的获取旅游信息,都显得特别重要.自助定制游将使旅游相关信息管理工作规范化、信息化、程序化,提供旅游景点、旅游线路,旅游新闻等服务本…...
文本编辑器去除PDF水印
用文本编辑器打开pdf,搜索水印的特殊文字,全部替换。 另外一个水印字母间有空格。 替换完后保存。 重新打开pdf:...
kubernetes负载感知调度
背景 kubernetes 的原生调度器只能通过资源请求来调度 pod,这很容易造成一系列负载不均的问题, 并且很多情况下业务方都是超额申请资源,因此在原生调度器时代我们针对业务的特性以及评估等级来设置 Requests/Limit 比例来提升资源利用效率。…...

Lock使用及效率分析(C#)
针对无Lock、Lock、ReadWriterLock、ReadWriterLockSlim四种方式,测试在连续写的情况下,读取的效率(原子操作Interlocked由于使用针对int,double等修改的地方特别多,而且使用范围受限,所以本文章没有测试) …...

安卓三防平板在行业应用中有哪些优势
在工业维修和检测中,安卓三防平板的应用也十分广泛。它可以搭载各种专业软件和工具,帮助工人们进行设备故障排查和维护,降低了维修成本和停机时间。 一、产品卖点: 1. 防水性能:该手持平板采用了防水设计,…...
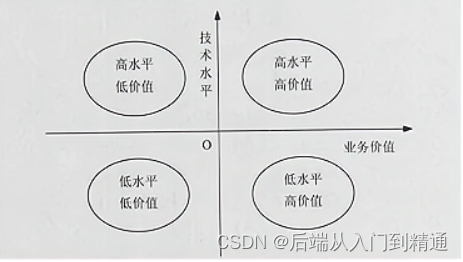
2015架构真题(五十)
供应链中信息流覆盖了供应商、制造商和分销商,信息流分为需求信息流和供应信息流,()属于需求信息流,()属于供应信息流。 库存记录生产计划商品入库单提货发运单 客户订单采购合同完工报告单销售…...
VScode Invoke-Expression: 无法将参数绑定到参数“Command”,因为该参数为空字符串
打开vscode时发生错误:Invoke-Expression : 无法将参数绑定到参数“Command”,因为该参数为空字符串。 解决办法:在anaconda prompt base中输入: conda upgrade -n base -c defaults --override-channels conda...

【图像融合】差异的高斯:一种简单有效的通用图像融合方法[用于融合红外和可见光图像、多焦点图像、多模态医学图像和多曝光图像](Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...

蓝桥杯 冶炼金属
原题目链接 🔧 冶炼金属转换率推测题解 📜 原题描述 小蓝有一个神奇的炉子用于将普通金属 O O O 冶炼成为一种特殊金属 X X X。这个炉子有一个属性叫转换率 V V V,是一个正整数,表示每 V V V 个普通金属 O O O 可以冶炼出 …...

嵌入式学习笔记DAY33(网络编程——TCP)
一、网络架构 C/S (client/server 客户端/服务器):由客户端和服务器端两个部分组成。客户端通常是用户使用的应用程序,负责提供用户界面和交互逻辑 ,接收用户输入,向服务器发送请求,并展示服务…...

Razor编程中@Html的方法使用大全
文章目录 1. 基础HTML辅助方法1.1 Html.ActionLink()1.2 Html.RouteLink()1.3 Html.Display() / Html.DisplayFor()1.4 Html.Editor() / Html.EditorFor()1.5 Html.Label() / Html.LabelFor()1.6 Html.TextBox() / Html.TextBoxFor() 2. 表单相关辅助方法2.1 Html.BeginForm() …...

Vue 模板语句的数据来源
🧩 Vue 模板语句的数据来源:全方位解析 Vue 模板(<template> 部分)中的表达式、指令绑定(如 v-bind, v-on)和插值({{ }})都在一个特定的作用域内求值。这个作用域由当前 组件…...
实现跳一跳小游戏)
鸿蒙(HarmonyOS5)实现跳一跳小游戏
下面我将介绍如何使用鸿蒙的ArkUI框架,实现一个简单的跳一跳小游戏。 1. 项目结构 src/main/ets/ ├── MainAbility │ ├── pages │ │ ├── Index.ets // 主页面 │ │ └── GamePage.ets // 游戏页面 │ └── model │ …...

针对药品仓库的效期管理问题,如何利用WMS系统“破局”
案例: 某医药分销企业,主要经营各类药品的批发与零售。由于药品的特殊性,效期管理至关重要,但该企业一直面临效期问题的困扰。在未使用WMS系统之前,其药品入库、存储、出库等环节的效期管理主要依赖人工记录与检查。库…...

Qwen系列之Qwen3解读:最强开源模型的细节拆解
文章目录 1.1分钟快览2.模型架构2.1.Dense模型2.2.MoE模型 3.预训练阶段3.1.数据3.2.训练3.3.评估 4.后训练阶段S1: 长链思维冷启动S2: 推理强化学习S3: 思考模式融合S4: 通用强化学习 5.全家桶中的小模型训练评估评估数据集评估细节评估效果弱智评估和民间Arena 分析展望 如果…...

【题解-洛谷】P10480 可达性统计
题目:P10480 可达性统计 题目描述 给定一张 N N N 个点 M M M 条边的有向无环图,分别统计从每个点出发能够到达的点的数量。 输入格式 第一行两个整数 N , M N,M N,M,接下来 M M M 行每行两个整数 x , y x,y x,y,表示从 …...
