当前位置：首页 > news >正文

『heqingchun-ubuntu系统下Qt报错connot find -lGL解决方法』

news 2025/12/15 15:02:47

ubuntu系统下Qt报错connot find -lGL解决方法

问题：
Qt报错
connot find -lGL
collect2:error:ld returned 1 exit status
解决方式：

cd /usr/lib/x86_64-linux-gnu

查看一下

ls | grep libGL

libGLdispatch.so.0
libGLdispatch.so.0.0.0
libGLESv2.so.2
libGLESv2.so.2.1.0
libGL.so.1
libGL.so.1.7.0
libGLU.so.1
libGLU.so.1.3.1
libGLX_indirect.so.0
libGLX_mesa.so.0
libGLX_mesa.so.0.0.0
libGLX.so.0
libGLX.so.0.0.0

发现：
没有名字为“libGL.so”的文件，只有“libGL.so.1”文件，那就链接一下：

sudo ln -s libGL.so.1 libGL.so

现在再执行Qt程序就可以找到libGL.so了，就不会报错了。
ubuntu系统下Qt报错connot find -lGL解决方法-完毕

『heqingchun-ubuntu系统下Qt报错connot find -lGL解决方法』

ubuntu系统下Qt报错connot find -lGL解决方法问题： Qt报错 connot find -lGL collect2:error:ld returned 1 exit status 解决方式： cd /usr/lib/x86_64-linux-gnu查看一下 ls | grep libGLlibGLdispatch.so.0 libGLdispatch.so.0.0.0 libGLESv2.so.…...

编程日记 2023/10/13 23:12:03

代码整洁之道：程序员的职业素养（十六）

辅导、学徒期与技艺导师的重要性在职业发展中是不可低估的。尽管最好的计算机科学学位教学计划可以提供坚实的理论基础，但面对实际工作中的挑战，年轻毕业生往往需要更多指导。幸运的是，有许多优秀的年轻人可以通过观察和模仿他们的导师来快…...

编程日记 2023/10/13 23:11:02

OSPF的原理与配置

第1章 OSPF[1] 本章阐述了OSPF协议的特征、术语，OSPF的路由器类型、网络类型、区域类型、LSA类型，OSPF报文的具体内容及作用，描述了OSPF的邻居关系，通过实例让读者掌握OSPF在各种场景中的配置。本章包含以下内容： …...

编程日记 2023/10/13 23:10:00

uni-app ：生成三位随机数、自定义全局变量、自定义全局函数、传参、多参数返回值

核心代码 function generateRandomNumber() {const min 100;const max 999;// 生成 min 到 max 之间的随机整数// Math.random() 函数返回一个大于等于 0 且小于 1 的随机浮点数。通过将其乘以 (max - min 1)，我们得到一个大于等于 0 且小于等于 (max - min 1…...

编程日记 2023/10/13 23:08:59

EF core 如何撤销对对象的更改

一般情况下 DB.SaveChanges() 就可以正常提交更改了. 但是如何撤销更改, 可以使用下面的代码. //撤销更改 //放弃更改. 防止后面的finally出错 DB.ChangeTracker.Entries().Where(e > e.Entity ! null).ToList().ForEach(e > e.State EntityState.Detached);...

编程日记 2023/10/13 23:07:58

以字符串mark作为分隔符，对字符串s进行分割

int main() {string s "How are you?";string mark " ";string tmp;int cur 0, first 0;//找到第一个标记while ((cur s.find_first_of(mark, cur)) ! string::npos){//获取第一个标记前的子串tmp s.substr(first, cur - first);cout << tmp …...

编程日记 2023/10/13 23:06:57

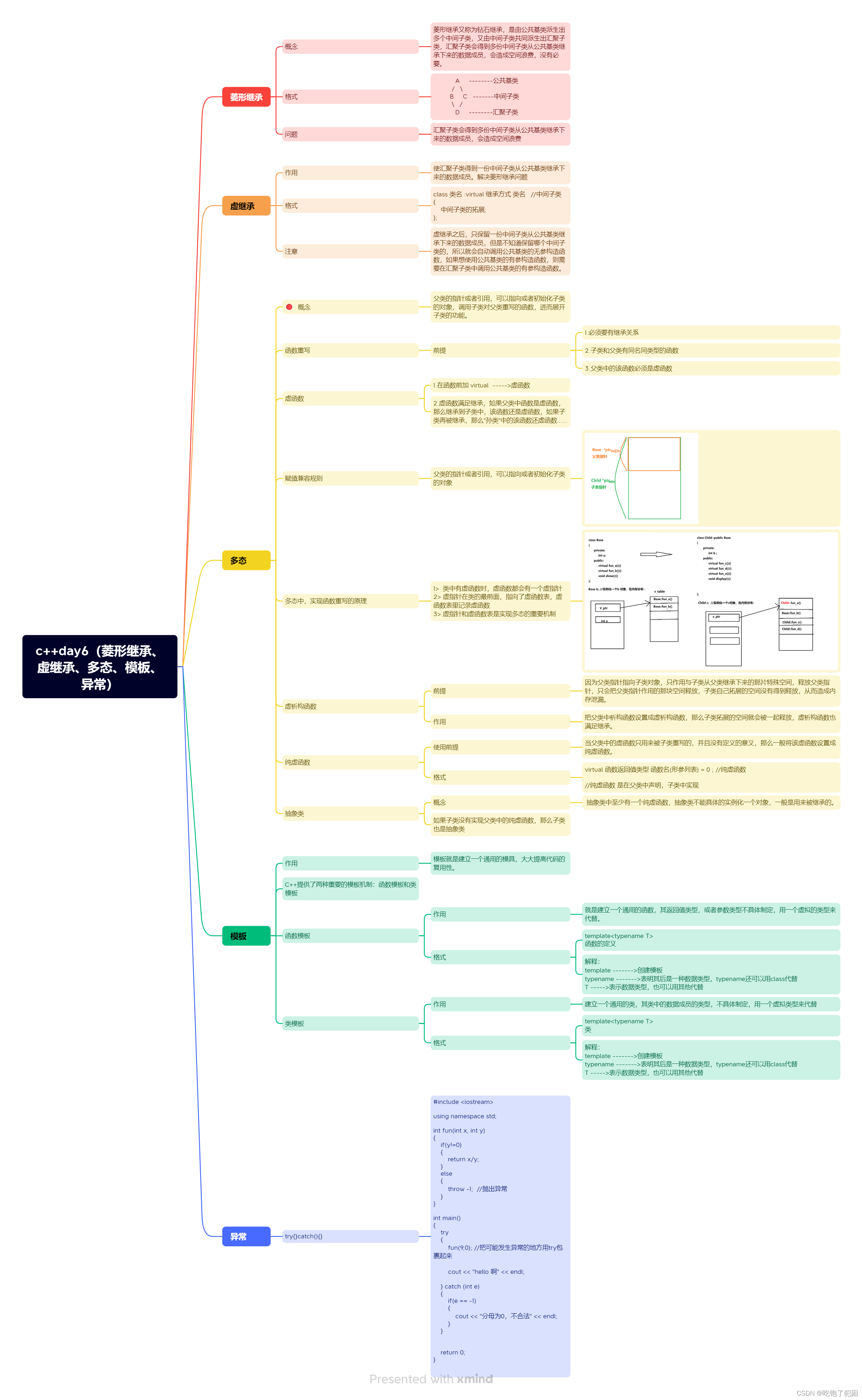
c++day6（菱形继承、虚继承、多态、模板、异常）

今日任务 1.思维导图 2.编程题： 代码： #include <iostream>using namespace std; /*以下是一个简单的比喻，将多态概念与生活中的实际情况相联系： 比喻：动物园的讲解员和动物表演想象一下你去了一家动物园&a…...

编程日记 2023/10/13 23:05:56

外卖跑腿系统开发的最佳实践和成功案例

外卖跑腿系统的开发既涉及技术实现，也需要考虑用户体验、运营策略和合规性。以下是一些最佳实践和一些成功的案例，以帮助您更好地理解这个领域的要点。 1. 技术框架的选择选择适合的技术框架是外卖跑腿系统成功的关键。您可以考虑使用以下技术&#…...

编程日记 2023/10/13 23:04:55

python中的range（）函数详解

range() 是 Python 内置的一个函数，用于生成一个整数序列。 range([start], [stop], [step])start、stop、step 分别表示序列的起始值、终止值和步长。start 和 step 是可选参数，如果不指定则默认为 0 和 1。一、range（）传递不…...

编程日记 2023/10/13 23:03:55

【taro react】 ---- 常用自定义 React Hooks 的实现【四】之遮罩层

1. 问题场景在实际开发中我们会遇到一个遮罩层会受到多个组件的操作影响，如果我们不采用 redux 之类的全局状态管理，而是选择组件之间的值传递，我们就会发现使用组件的变量来控制组件的显示和隐藏很不方便，更不要说像遮罩层这样一个项目多处使用的公共组件，他的隐藏和显示…...

编程日记 2023/10/13 23:02:54

【git】git命令行

首先要了解git整个流程的一个分类： workspace：工作区staging area：暂存区/缓存区local repository：版本库或本地仓库remote repository：远程仓库创建仓库 git clone gitgithub.comxxxxxxxxxxxx//拷贝一份远程仓库 …...

编程日记 2023/10/13 23:01:53

centos8 jenkins 搭建和使用

一、安装jenkins 直接war包搭建下载地址：https://get.jenkins.io/war-stable/ 下载稳定长期版本二、jenkins 启动依赖java, 安装java sdk ，好像支持java 11和17版本，21版本不支持会报错下载sdk地址，https://www.oracle.com/j…...

编程日记 2023/10/13 23:00:51

Hive实战(03)-深入了解Hive JDBC：在大数据世界中实现数据交互

在大数据领域，Hive作为一种数据仓库解决方案，为用户提供了一种SQL接口来查询和分析存储在Hadoop集群中的数据。为了更灵活地与Hive进行交互，我们可以使用Hive JDBC（Java Database Connectivity）驱动程序。本文将深入探…...

编程日记 2023/10/13 22:59:50

SQL开发笔记之专栏介绍

Sql是用于访问和处理数据库的标准计算机语言，使用SQL访问和处理数据系统中的数据，这类数据库包括：Mysql、PostgresSql、Oracle、Sybase、DB2等等，数据库无非围绕着“增删改查”的核心业务进行开发。并且目前绝大多数的后端程序开发…...

编程日记 2023/10/13 22:58:48

华为OD机考算法题：找终点

目录题目部分解读与分析代码实现题目部分题目找终点难度易题目说明给定一个正整数数组，设为nums，最大为100个成员，求从第一个成员开始，正好走到数组最后一个成员，所使用的最少步骤数。要求： 1.第…...

编程日记 2023/10/13 22:57:47

el-table通过scope.row获取表格每列的值，以及scope.$index

<el-table-column type"selection" width"55"></el-table-column><el-table-column prop"id" label"ID" width"80"></el-table-column><el-table-column prop"name" label"文件名…...

编程日记 2023/10/13 22:56:46

uni-app：本地缓存的使用

uni-app 提供了多种方法用于本地缓存的操作。下面是一些常用的 uni-app 本地缓存方法： uni.setStorageSync(key, data): 同步方式将数据存储到本地缓存中，可以使用对应的 key 来获取该数据。 uni.setStorage({key, data}): 异步方式将数据存储到本地缓存…...

编程日记 2023/10/13 22:54:44

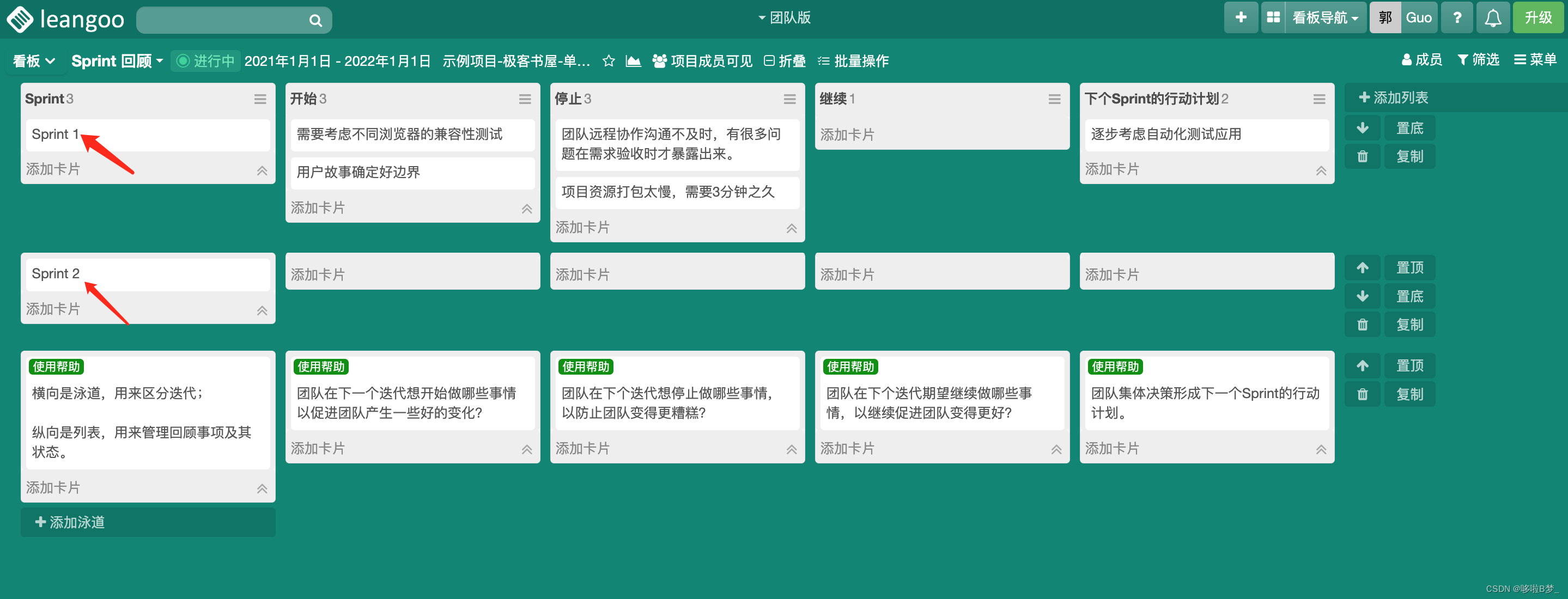
在Scrum敏捷开发中，开发人员（Developers）的职责

在Scrum敏捷开发中，开发人员（Developers）是Scrum团队中最重要的角色之一，负责产品的开发和交付，其重要性不言而喻。那开发人员的职责和需要参加的活动是什么呢？ Developers核心职责： 承诺并完…...

编程日记 2023/10/13 22:53:42

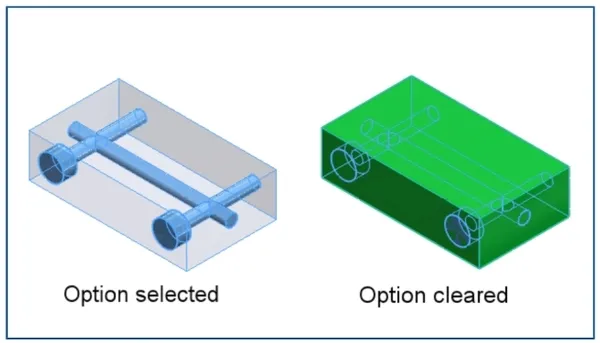
SOLIDWORKS® 2024 新功能 - 3D CAD

1、先前版本的兼容性 • 利用您订阅的 SOLIDWORKS，可将您的 SOLIDWORKS 设计作品保存为旧版本，与使用旧版本 SOLIDWORKS 的供应商无缝协作。 • 可将零件、装配体和工程图保存为新版本前两年之内的SOLIDWORKS 版本。优点： 即使其他用户正…...

编程日记 2023/10/13 22:52:41

系统架构设计：20 论软件需求管理

目录一需求工程 1 需求开发 1.1 需求获取 1.1.1 软件需求的分类 1.1.2 需求获取方法...

编程日记 2023/10/13 22:51:41

网络六边形受到攻击

大家读完觉得有帮助记得关注和点赞！！！ 抽象现代智能交通系统 （ITS） 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 （…...

编程新知 2025/12/12 19:56:45

CTF show Web 红包题第六弹

提示 1.不是SQL注入 2.需要找关键源码思路进入页面发现是一个登录框，很难让人不联想到SQL注入，但提示都说了不是SQL注入，所以就不往这方面想了先查看一下网页源码，发现一段JavaScript代码，有一个关键类ctfs…...

编程新知 2025/12/12 0:52:22

深入浅出：JavaScript 中的 `window.crypto.getRandomValues()` 方法

深入浅出：JavaScript 中的 window.crypto.getRandomValues() 方法在现代 Web 开发中，随机数的生成看似简单，却隐藏着许多玄机。无论是生成密码、加密密钥，还是创建安全令牌，随机数的质量直接关系到系统的安全性。Jav…...

编程新知 2025/10/8 4:56:09

连锁超市冷库节能解决方案：如何实现超市降本增效

在连锁超市冷库运营中，高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术，实现年省电费15%-60%，且不改动原有装备、安装快捷、…...

编程新知 2025/11/30 16:55:29

【AI学习】三、AI算法中的向量

在人工智能（AI）算法中，向量（Vector）是一种将现实世界中的数据（如图像、文本、音频等）转化为计算机可处理的数值型特征表示的工具。它是连接人类认知（如语义、视觉特征）与…...

编程新知 2025/8/12 22:58:13

【git】把本地更改提交远程新分支feature_g

创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

编程新知 2025/12/13 4:20:30

06 Deep learning神经网络编程基础激活函数 --吴恩达

深度学习激活函数详解一、核心作用引入非线性：使神经网络可学习复杂模式控制输出范围：如Sigmoid将输出限制在(0,1)梯度传递：影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...

编程新知 2025/11/17 21:48:26

dify打造数据可视化图表

一、概述在日常工作和学习中，我们经常需要和数据打交道。无论是分析报告、项目展示，还是简单的数据洞察，一个清晰直观的图表，往往能胜过千言万语。一款能让数据可视化变得超级简单的 MCP Server，由蚂蚁集团 AntV 团队…...

编程新知 2025/12/5 14:12:22

GC1808高性能24位立体声音频ADC芯片解析

1. 芯片概述 GC1808是一款24位立体声音频模数转换器（ADC），支持8kHz~96kHz采样率，集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器，适用于高保真音频采集场景。 2. 核心特性高精度：24位分辨率&#xff0c…...

编程新知 2025/12/15 14:40:07

AGain DB和倍数增益的关系

我在设置一款索尼CMOS芯片时，Again增益0db变化为6DB，画面的变化只有2倍DN的增益，比如10变为20。这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析： 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...

编程新知 2025/9/30 16:23:57

ubuntu系统下Qt报错connot find -lGL解决方法

相关文章：