Ps：选区的布尔运算
选区的布尔 Boolean运算指的是选区之间的相加（并集）、相减（差集）以及相交（交集），从而形成一个新的选区。
◆ ◆ ◆
使用工具选项栏
在 Ps 中，几乎所有的选区工具的工具选项栏上都有这四个按钮，如下图所示。
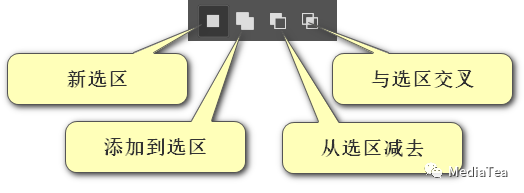
新选区
New selection
默认选项。
在此选项时，若画布中无选区，则创建新选区。
若画布中有选区，则新选区替换原来的选区。
添加到选区
Add to selection
将新绘制的选区添加到已有选区。
从选区减去
Subtract from selection
从已有选区中减去新绘制的区域。
与选区交叉
Intersect with selection
仅保留与已有选区相交的区域。
说明：
在实质操作时，建议保持在启用“新选区”按钮状态，并使用辅助键进行切换。注意观察鼠标形状的变化。
按住 Shift 键，添加到选区。按住 Alt 键，从选区减去。按住 Alt + Shift 键，与选区相交。
◆ ◆ ◆
使用图层面板
按住 Ctrl 键点击图层面板上的图层缩览图，可基于图层像素的透明度 Transparency将其载入为新的选区。不透明的完全选择，透明的则不选择，半透明的局部选择。
按住 Ctrl + Alt 键点击图层缩览图，则从当前画布上已有的选区中减去。按住 Ctrl + Alt + Shift 键点击图层缩览图，则与当前画布上已有的选区相交。
以上操作也可以在选中图层之后通过菜单命令来实现。
Ps菜单：选择/载入选区
Select/Load Selection
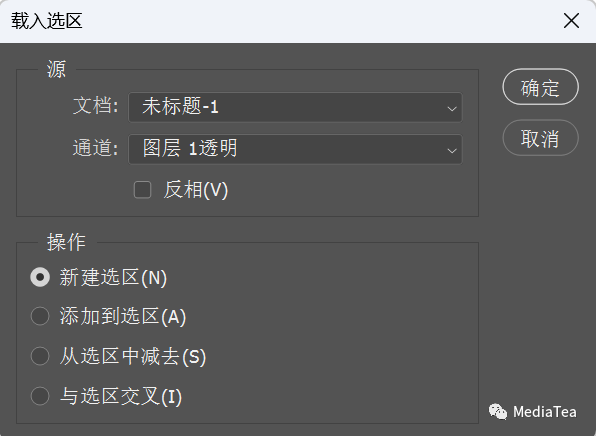
还可以从“通道”列表中选择当前图层的图层蒙版（如果有的话）或者是已建好的 Alpha 通道。
◆ ◆ ◆
使用通道或蒙版
Alpha 通道或蒙版本身存储的就是选区信息。白色代表选择，黑色代表不选择，灰色代表局部选择。
按住 Ctrl 键点击通道缩览图或蒙版缩览图，可将其载入为新的选区。
按住 Ctrl + Alt 键点击通道缩览图或蒙版缩览图，则从已有的选区中减去。按住 Ctrl + Alt + Shift 键点击通道缩览图或蒙版缩览图，则与已有的选区相交。
如果 Alpha 通道或图层蒙版上有灰色区域（即半透明区域），按住 Ctrl + Alt + Shift 键连续点击缩览图可渐次收缩选区。
对于原色通道，也可以按上述方式处理，同样也是基于通道上的黑白灰信息来创建选区。
对于复合通道，则是基于明度信息（本质上也是黑白灰）创建选区。
“点赞有美意，赞赏是鼓励”
相关文章：
Ps：选区的布尔运算
选区的布尔 Boolean运算指的是选区之间的相加（并集）、相减（差集）以及相交（交集），从而形成一个新的选区。 ◆ ◆ ◆ 使用工具选项栏 在 Ps 中，几乎所有的选区工具的工具选项栏上都有…...
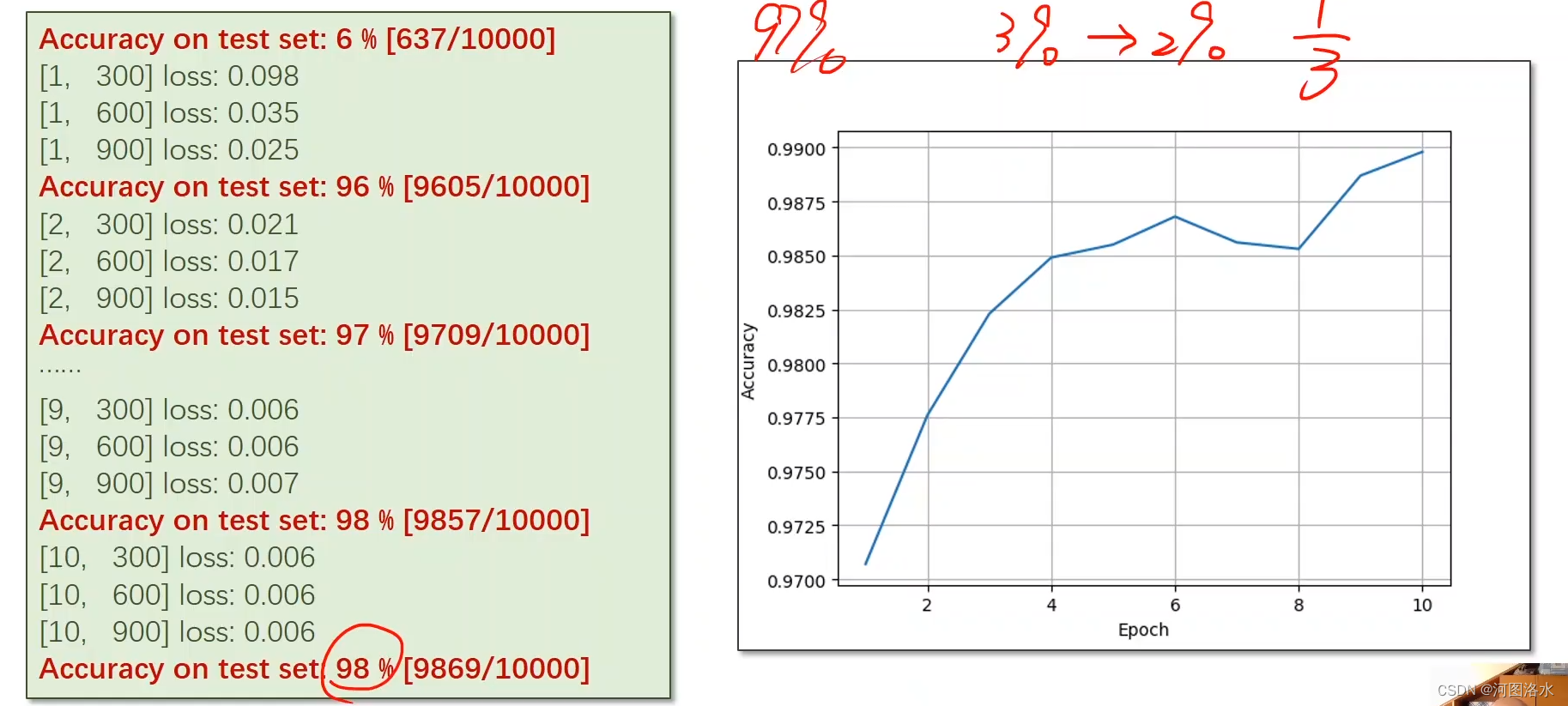
PyTorch 深度学习之卷积神经网络(基础篇)Basic CNN(九)
0. Revision: Fully connected Neural Network 全连接 1. Convolution Neural Network 保留空间信息 1.1 Convolution Convolution-Single Input Channel 单通道 数乘 3 input Channels 3通道 N input Channels N input Channels and M output channel M 个卷积核 1.2 conv…...
torch实现Gated PixelCNN
文章目录 PixelCNNGated PixelCNN PixelCNN import torch import torch.nn as nn import torch.nn.functional as F# Pixel CNNclass MaskConv2d(nn.Module):def __init__(self, conv_type, *args, **kwags):super().__init__()assert conv_type in (A, B)self.conv nn.Conv2…...
破局「二次创业」：合思的新解法
在新的水温下，寻找更为良性的发展正在成为企业的必答题。对此，合思给出的不仅是一份更“省”的答题方法。也更是从认知层到行动层，最后到工具层的一张授人以渔的“渔网”。 作者|思杭 编辑|皮爷 出品|产业家 今年4月初，广州…...
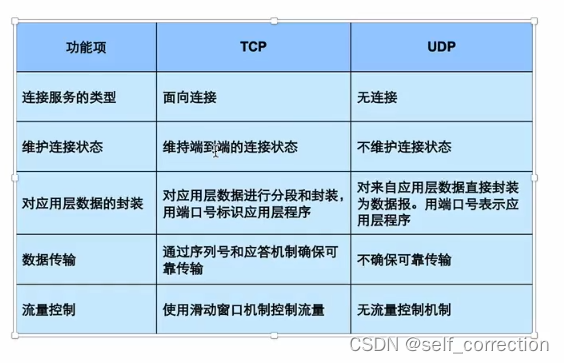
第五章：TCP和UDP基本原理
TCP和UDP基本原理 一、TCP/IP传输层的作用二、 端口1.范围2. 服务端3. 客户端4. 常见知名端口号4.1 TCP 80 HTTP4.2 TCP 20 21 FTP4.3 TCP 23 TELNET4.4 TCP 25 SMTP4.5 UDP 53 DNS4.6 TCP 443 HTTPS 三、 TCP原理1. TCP头部封装格式1.1 Source Port 源端口1.2 Destination Por…...
算法：动态规划的入门理解
文章目录 算法原理题目解析第n个泰波那契数列三步问题使用最小花费爬楼梯 从本篇开始总结的是动态规划的一些内容，动态规划是算法中非常重要的一个版块，因此也是学习算法中的一个重点，在学习动态规划前应当要把动态规划的基础知识学习一下 算…...
最新版nacos 2.2.3服务注册与发现版本依赖问题
最新版nacos的注册服务时配置文件写的是对的，但就是在nacos web页面无法看见服务，此时你需要注意你的依赖是否正确 spring: application:name: orderservicecloud:nacos:discovery:server-addr: 122.51.115.127:8848父工程依赖：现在最新的s…...
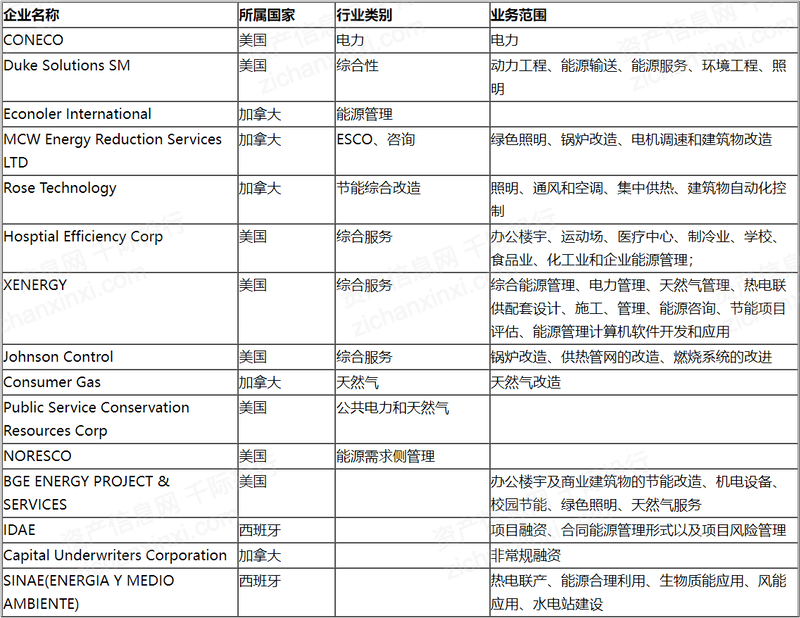
2023年中国合同能源管理行业研究报告
第一章 行业概况 1.1 定义及分类 合同能源管理 (Energy Performance Contracting, EPC) 是当前能源行业中一个重要的概念，它构建了一个桥梁，将节能服务公司 (Energy Management Company, EMCo) 与用能单位紧密联系在一起。通过特定的契约形式ÿ…...
php以半小时为单位，输出指定的时间范围
//可预订小时范围$hour [];for ($i$startHour*3600;$i<$endHour*3600;$i1800){//以半小时为单位输出$startHourItem date(H:i,strtotime(date(Y-m-d))$i);//小时开始$endHourItem date(H:i,strtotime(date(Y-m-d))$i1800);//当前时间再加半小时$hourItemStr $startHourI…...
Electron应用的 asar 打包 解压
前言： .asar文件是一种归档文件格式，通常用于封装Electron应用程序的资源。Electron是一个使得开发者能够使用Web技术构建跨平台桌面应用程序的框架。为了提高性能和简化部署，Electron应用程序的资源通常会被打包到一个.asar文件中。 安装 as…...
蓝桥等考Python组别十七级003
第一部分：选择题 1、Python L17 （15分） 运行下面程序，输出的结果是（ ）。 def func(x, y): return (x + y) // 3 print(func(7, 5)) 2468正确答案：B 2、Python L17 （15</...
Redis概述和与SpringBoot的整合
Redis是一种高性能的键值对存储数据库，它支持多种数据结构，包括字符串、哈希、列表、集合和有序集合等。Redis具有快速、可靠、灵活和可扩展等特点，也被广泛应用于缓存、队列和排行榜等场景。 SpringBoot是一种基于Spring框架的快速开发脚手…...
 函数：实现精确的数值舍入操作)
Python 中的 round() 函数：实现精确的数值舍入操作
round(x, n) 函数用于对数值 x 进行舍入操作，并指定保留的小数位数为 n。它的工作原理如下： 如果 x 的小数位数小于等于 n，则直接返回 x 本身。例如，round(3.1415, 2) 将返回 3.14。 如果 x 的小数位数大于 n，则按照四…...
在springboot中如何开启Bean数据校验
①：添加JSR303规范坐标与Hibernate校验框架对应坐标 <dependency><groupId>javax.validation</groupId><artifactId>validation-api</artifactId> </dependency><dependency><groupId>org.hibernate.validator<…...
【C语言好题系列三】
文章目录 学习导航一. 选择题二. 编程题(力扣/牛客网）三. 总结 学习导航 一. 选择题 如下程序的运行结果是（D） char c[5]{a, b, \0, c, \0}; printf("%s", c);A: ‘a’ ‘b’ B: ab\0c\0 C: ab c D: ab 答案解析： 正…...
ElasticSearch搜索引擎：常用的存储mapping配置项 与 doc_values详细介绍
一、ES的数据存储结构： ES底层使用 Lucene 存储数据，Lucene 的索引包含以下部分： A Lucene index is made of several components: an inverted index, a bkd tree, a column store (doc values), a document store (stored fields) and te…...
[Spring]事务的传播机制
一、背景 Mysql在修改完数据后，默认会自动触发事务Commit提交。 而在我们服务的一个方法里，需要多次修改Mysql记录。 为了保证原子性，我们需要将Mysql设为手动提交，多次修改后再commit提交。 二、Spring事务 1、编程式事务管理…...
linux下，如何查看一个文件的哈希值md5以及sha264
在linux终端中，可能存在多个相似的文件，而哈希值可以唯一确定一个文件。文件的哈希值计算可以有以下两种方式，MD5和SHA256，现将两种方式罗列如下： 1、MD5 命令：$ md5sum FileName 一个文件的 MD5 是固定的…...
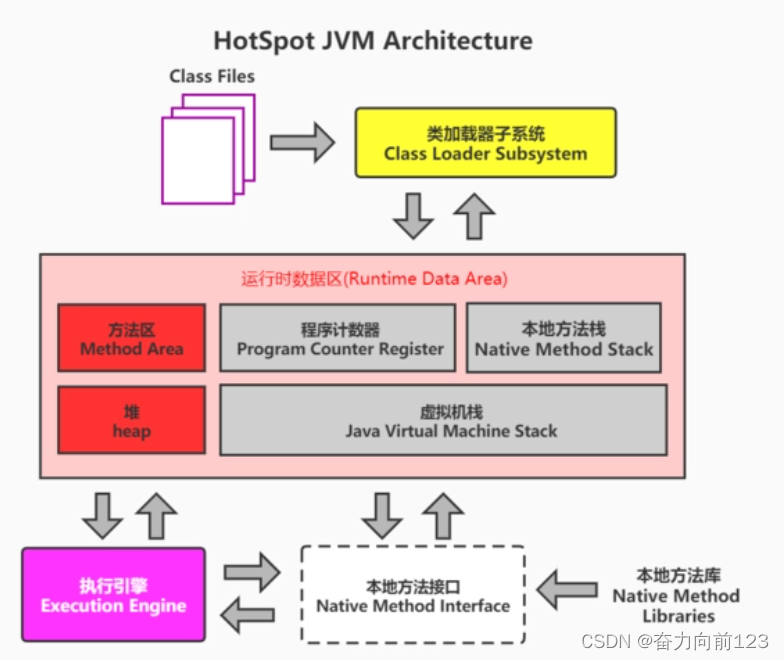
Java类加载过程
一、前言 我们都知道计算机的底层逻辑都是0和1的编码，当然除了现在所研究的量子计算除外。那么我们在计算机所做的一切操作，底层原理是不是都可以翻译到0和1呢。如果刨根问底的话，可以这么说，当然0和1的表示也属于逻辑门电路电的…...
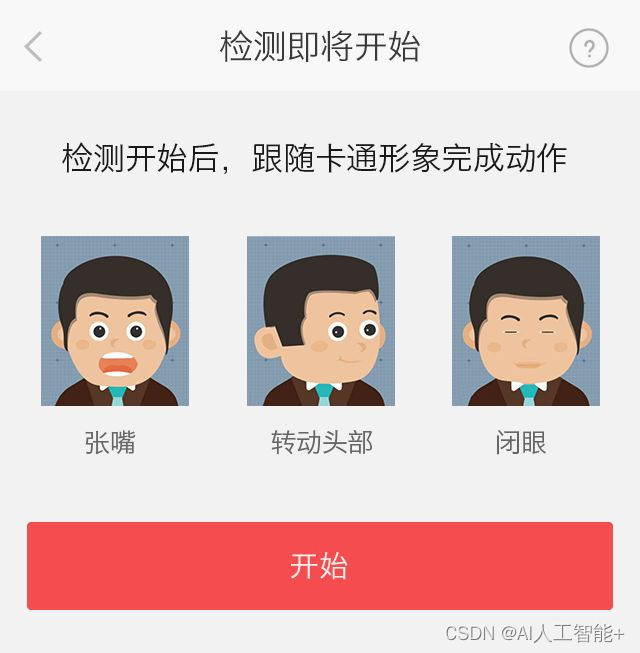
人脸活体检测技术的应用，有效避免人脸识别容易被攻击的缺陷
随着软件算法和物理终端的进步，人脸识别现在越来越被广泛运用到生活的方方面面，已经成为了重要的身份验证手段，但同时也存在着自身的缺陷，目前常规人脸识别技术可以精准识别目标人像特征，并迅速返回比对结果࿰…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 （1）连接查询（JOIN） 内连接（INNER JOIN）：返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...
Cesium1.95中高性能加载1500个点
一、基本方式： 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...
NLP学习路线图（二十三）：长短期记忆网络（LSTM）
在自然语言处理（NLP）领域，我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感，还是实现语言的翻译，都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心，而循环神经网络（RNN） 曾被视为…...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入（联动）2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...
HashMap中的put方法执行流程（流程图）
1 put操作整体流程 HashMap 的 put 操作是其最核心的功能之一。在 JDK 1.8 及以后版本中，其主要逻辑封装在 putVal 这个内部方法中。整个过程大致如下： 初始判断与哈希计算： 首先，putVal 方法会检查当前的 table（也就…...
基于Java+MySQL实现（GUI）客户管理系统
客户资料管理系统的设计与实现 第一章 需求分析 1.1 需求总体介绍 本项目为了方便维护客户信息为了方便维护客户信息，对客户进行统一管理，可以把所有客户信息录入系统，进行维护和统计功能。可通过文件的方式保存相关录入数据，对…...
uniapp手机号一键登录保姆级教程（包含前端和后端）
目录 前置条件创建uniapp项目并关联uniClound云空间开启一键登录模块并开通一键登录服务编写云函数并上传部署获取手机号流程(第一种) 前端直接调用云函数获取手机号（第三种）后台调用云函数获取手机号 错误码常见问题 前置条件 手机安装有sim卡手机开启…...
Golang——9、反射和文件操作
反射和文件操作 1、反射1.1、reflect.TypeOf()获取任意值的类型对象1.2、reflect.ValueOf()1.3、结构体反射 2、文件操作2.1、os.Open()打开文件2.2、方式一：使用Read()读取文件2.3、方式二：bufio读取文件2.4、方式三：os.ReadFile读取2.5、写…...
【Linux系统】Linux环境变量：系统配置的隐形指挥官
。# Linux系列 文章目录 前言一、环境变量的概念二、常见的环境变量三、环境变量特点及其相关指令3.1 环境变量的全局性3.2、环境变量的生命周期 四、环境变量的组织方式五、C语言对环境变量的操作5.1 设置环境变量：setenv5.2 删除环境变量:unsetenv5.3 遍历所有环境…...
在 Spring Boot 项目里，MYSQL中json类型字段使用
前言： 因为程序特殊需求导致，需要mysql数据库存储json类型数据，因此记录一下使用流程 1.java实体中新增字段 private List<User> users 2.增加mybatis-plus注解 TableField(typeHandler FastjsonTypeHandler.class) private Lis…...