494.目标和

1. 回溯算法
这题和之前做的那些排列、组合的回溯稍微有些不同,你不需要每次选数据时都是for遍历去选择,很明显这是顺序选择的
比如 数组[0,1],target=1;
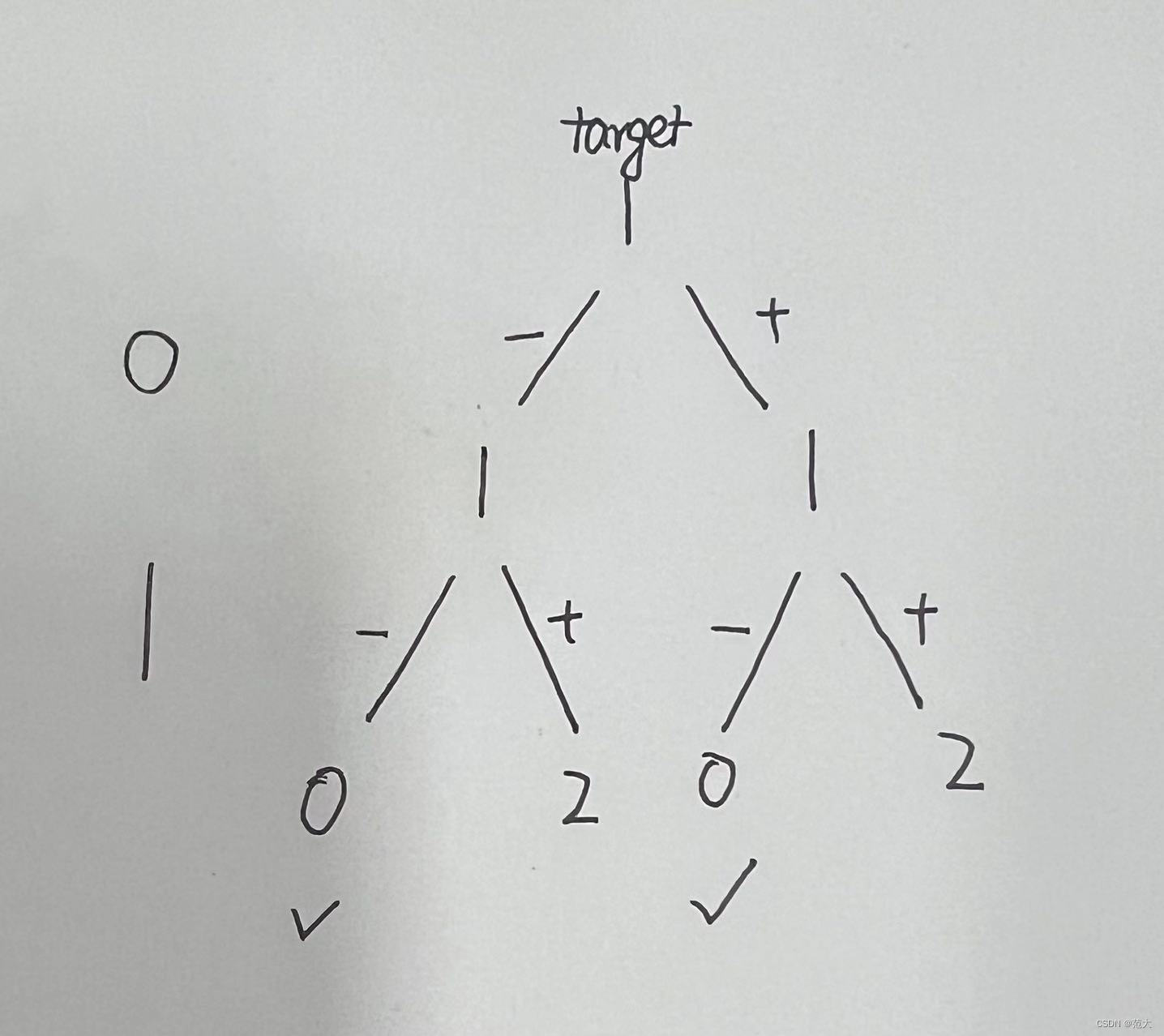
递归数组,每个元素都 + 或者 - ,然后取最后结果为0的即可
class Solution {public int findTargetSumWays(int[] nums, int target) {find(0,nums,target);return count;}private void find(int begin,int[] nums,int target){// 如果减完了,结束if(begin == nums.length){if(target == 0){count++;}return;}target-=nums[begin];find(begin+1,nums,target);target+=nums[begin];target+=nums[begin];find(begin+1,nums,target);target-=nums[begin]; }private int count=0;
}
2. 动态规划
这其实可以抽象为0/1背包问题。
数组中的元素,要么是前面+,要么是前面-,问计算结果为target的方案有多少种。
计算结果为0,即我们把前面为+的元素放在一个集合A中,前面为-的元素放在一个集合B中,二者之差为target即可。
我们如果知道了集合A,那么集合B自然就是数组中剩余元素组成。
可以列个简单的数学公式,假设A集合元素的和为left,B元素和为right,数组总和为sum
left + right = sum;
left - right = target;
二者一相加可以得到 left=(sum+target)/2;
由于都是正整数,left如果不是正整数,说明无解,即没有这种方案。
思路成功转换为,背包容量为left,在数组中找出和刚好为left的方案,并记录方案的最大数。
- 确定dp[i][j]
即dp[i][j] :在数组中下标为0~i的元素中任选,和刚好为j的方案数量
-
确定递推公式
如果第i个元素不选,那方案数量和dp[i-1][j]的一样
dp[i][j] = dp[i-1][j]
如果选了第i个元素,那方案就不仅仅从i-1个元素选出和为j的,从i-1个元素选出和为j-nums[i]的也可以,两种方案数相加。
dp[i][j] = dp[i-1][j] + dp[i-1][j-nums[i]] -
如何初始化
dp[0][0]=1 我可以都不选,那方案数就是1
初始化第一行 dp[0][nums[0]]+=1;
题目中提示给出nums[i]范围是可能为0,所以如果nums[0]=0,那就是dp[0][0]中都不选的方案中,再添加一种,选择元素0,那就是两个方案了!!!
重点细节,卡了我一个上午!!! -
确定遍历顺序
先数组元素,再背包容量 -
模拟推导
class Solution {public int findTargetSumWays(int[] nums, int target) {if(nums.length == 1){return target == nums[0]?1:target == 0-nums[0]?1:0;}// 把集合分成前面放+的正集合和前面放-的负集合.正集合的和为left,负集合的和为right// left+right=sum left-right=target => left = (target+sum)/2// 即转换为问题---把背包容量为left的背包装满有多少种方案// 同时,如果left不为整数,说明不行,返回0// dp[i][j] 在下标0为~i的元素中,填满背包容量为j,有多少种方案// dp[i][j] = dp[i-1][j] 如果不装i// dp[i][j] = Math.max(dp[i-1][j-nums[i]],dp[i-1][j]) 如果装iint sum=0;for(int i:nums){sum += i;}if((target+sum)%2 != 0 ){return 0;}if(target > sum || target < -sum){return 0;}int num = (target+sum)/2;num = num < 0?-num:num;int[][] dp = new int[nums.length][num+1];// 当容量为0的时候,都不选就是一种方案for(int i=0;i<nums.length;i++){dp[i][0]=1;}// 遍历第一行,dp[0][nums[0]]+=1 因为可能第一行中nums[0]=0,此时dp[0][0]其实已经初始化为1了,但是dp[0][0]其实有两个方案的,一个是都不选,一个是选了0,这个细节决定了我们后续的遍历从第二行开始是否成功!!!if(nums[0]<num+1){dp[0][nums[0]]+=1;}for(int i=1;i<nums.length;i++){for(int j=0;j<num+1;j++){dp[i][j] = dp[i-1][j];if(j>=nums[i]){dp[i][j] = dp[i-1][j-nums[i]] + dp[i-1][j]; } }}return dp[nums.length-1][num];}
}
优化成一维的
class Solution {public int findTargetSumWays(int[] nums, int target) {if(nums.length == 1){return target == nums[0]?1:target == 0-nums[0]?1:0;}// 把集合分成前面放+的正集合和前面放-的负集合.正集合的和为left,负集合的和为right// left+right=sum left-right=target => left = (target+sum)/2// 即转换为问题---把背包容量为left的背包装满有多少种方案// 同时,如果left不为整数,说明不行,返回0// dp[i][j] 在下标0为~i的元素中,填满背包容量为j,有多少种方案// dp[i][j] = dp[i-1][j] 如果不装i// dp[i][j] = Math.max(dp[i-1][j-nums[i]],dp[i-1][j]) 如果装iint sum=0;for(int i:nums){sum += i;}if((target+sum)%2 != 0 ){return 0;}if(target > sum || target < -sum){return 0;}int num = (target+sum)/2;num = num < 0?-num:num;int[]dp = new int[num+1];// 当容量为0的时候,都不选就是一种方案dp[0]=1;// 遍历第一行if(nums[0]<num+1){dp[nums[0]]+=1;}for(int i=1;i<nums.length;i++){for(int j=num;j>=nums[i];j--){dp[j] += dp[j-nums[i]]; }}return dp[num];}
}
这道题很经典,建议过段时间重复刷
相关文章:
494.目标和
1. 回溯算法 这题和之前做的那些排列、组合的回溯稍微有些不同,你不需要每次选数据时都是for遍历去选择,很明显这是顺序选择的 比如 数组[0,1],target1; 递归数组,每个元素都 或者 - ,然后取最后结果为0…...

滑台模组的应用有哪些?
在自动化生产中,我们常常会看到滑台模组的身影,那么,滑台模组究竟在自动化生产设备中起着怎样的作用呢? 简单点说,滑台模组由滑块、滚珠丝杆、导轨、主体等其它传动零件组成的自动化晋级单元,经过各单元的组…...
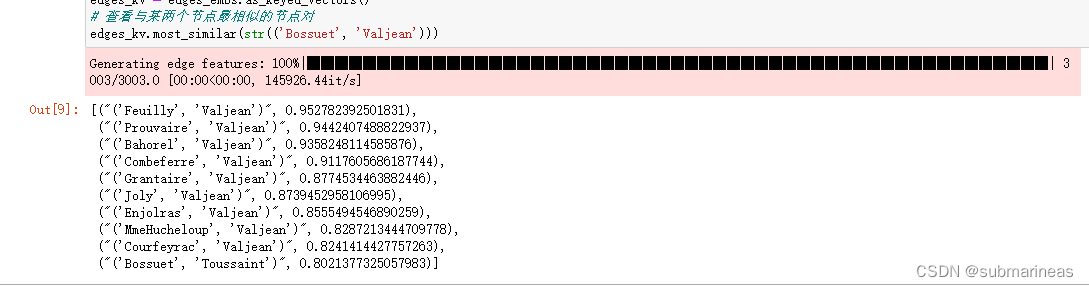
CS224W课程学习笔记(四):node2vec算法原理与说明
引言 什么是图嵌入? 我想从上节的deepwalk中已经有一个十分完整的轮廓了,这里引出deepwalk论文中的一张很形象的图(当然,上节的一些实战演练,也将这种嵌入关系进行了模拟与可视化,前文为:&…...

扩展lucas定理
前置知识: lucas定理中国剩余定理 介绍 当正整数n,mn,mn,m很大,且质数ppp较小的时候,要求CnmC_n^mCnm对ppp取模后的值,可以用lucas定理。 但如果ppp不是质数,那该怎么办呢?如果mmm较小,则…...
医疗影像工具LEADTOOLS 入门教程: 从 PDF 中提取附件 - 控制台 C#
LEADTOOLS 是一个综合工具包的集合,用于将识别、文档、医疗、成像和多媒体技术整合到桌面、服务器、平板电脑、网络和移动解决方案中,是一项企业级文档自动化解决方案,有捕捉,OCR,OMR,表单识别和处理&#…...
【LVGL】学习笔记--(1)Keil中嵌入式系统移植LVGL
一 LVGL简介最近emwin用的比较烦躁,同时被LVGL酷炫的界面吸引到了,所以准备换用LVGL试试水。LVGL(轻量级和通用图形库)是一个免费和开源的图形库,它提供了创建嵌入式GUI所需的一切,具有易于使用的图形元素,美丽的视觉效…...
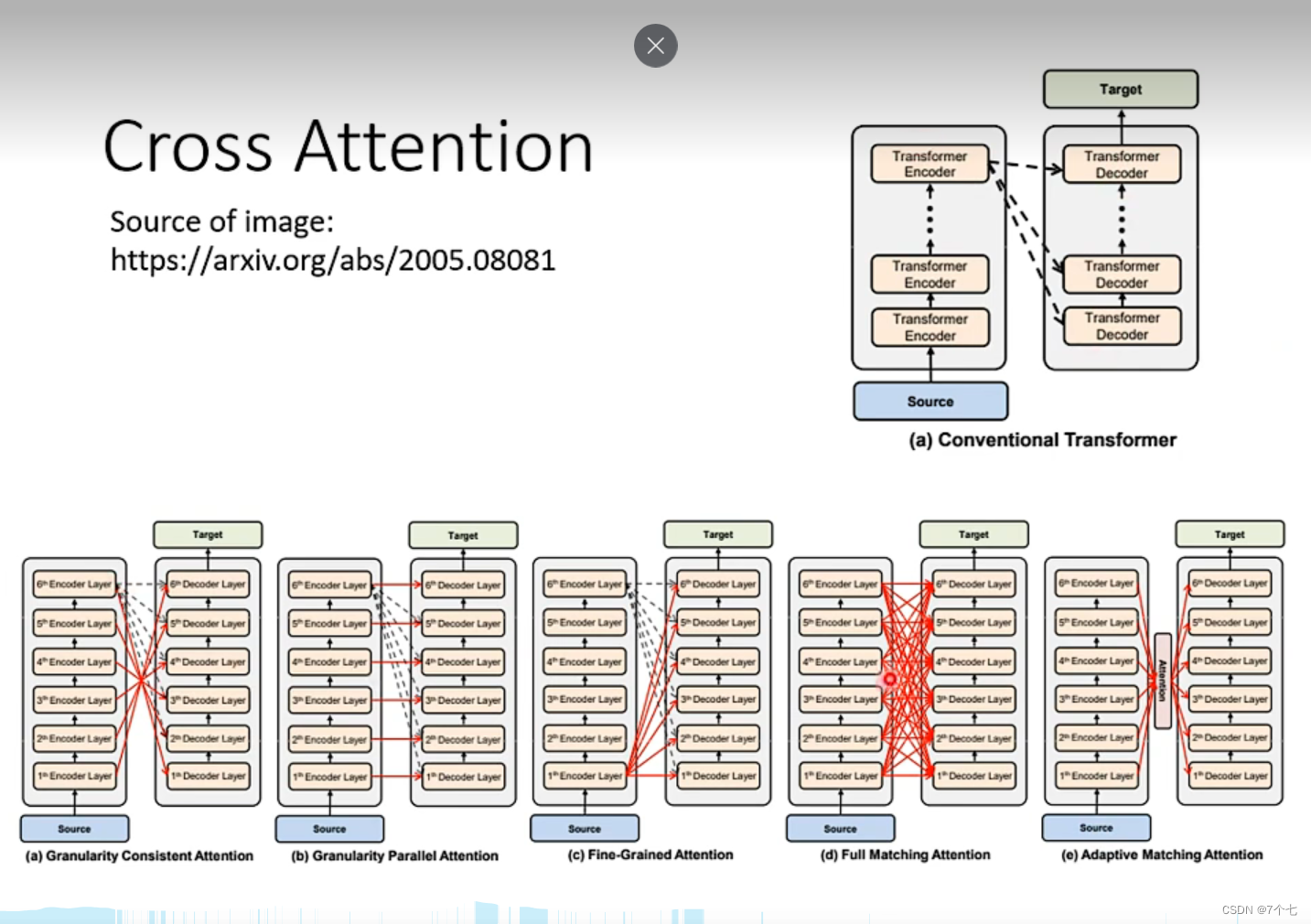
Transformer学习笔记
Transformer学习笔记1. 参考2. 模型图3.encoder部分3.1 Positional Encoding3.2 Muti-Head Attention3.3 ADD--残差连接3.4 Norm标准化3.5 单个Transformer Encoder流程图4.decoder部分4.1 mask Muti-Head Attention4.2 Muti-Head Attention5 多个Transformer Encoder和多个Tra…...
vue-cli引入wangEditor、Element,封装可上传附件的富文本编辑器组件(附源代码直接应用,菜单可调整)
关于Element安装引入,请参考我的另一篇文章:vue-cli引入Element Plus(element-ui),修改主题变量,定义全局样式_shawxlee的博客-CSDN博客_chalk variables 1、安装wangeditor npm i wangeditor --savewangE…...

移动办公时代,数智化平台如何赋能企业管理升级?
在传统的办公模式下,企业组织办公不仅时效低,周期长、成本高,且各办公系统相互独立。随着社会经济的发展,人们的工作生活变得多样化,对于办公的需求也越来越多,存在明显弊端的传统办公模式已不能满足企业对…...

2023“拼夕夕”为什么可以凭借简单的拼团做这么大?
2023“拼夕夕”为什么可以凭借简单的拼团做这么大? 2023-02-24 梦龙 大家好,我是你们熟悉而又陌生的好朋友梦龙,一个创业期的年轻人 大家都知道,拼夕夕背后的商业模式是拼团,但是大家知道为什么简单的拼团可以让拼夕…...
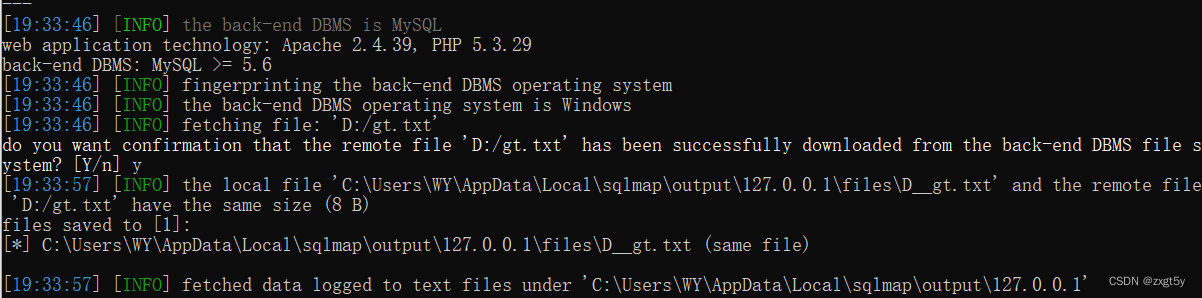
sqlmap工具
sqlmap Sqlmap是一个开源的渗透测试工具,可以用来自动化的检测,利用SQL注入漏洞,获取数据库服务器的权限。目前支持的数据库有MySQL、Oracle、PostgreSQL、Microsoft SQL Server、Microsoft Access等大多数据库 Sqlmap采用了以下5种独特的SQ…...
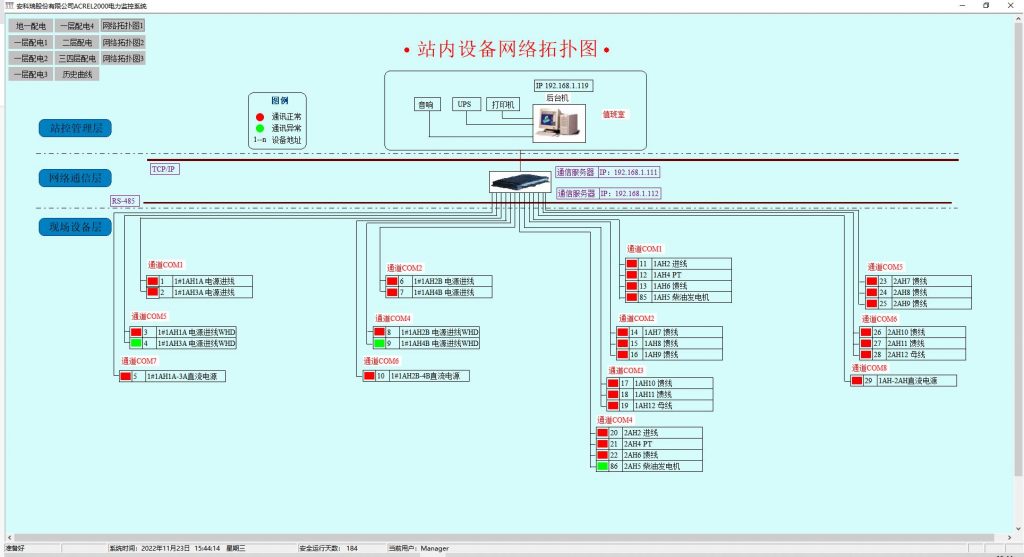
高/低压供配电系统设计——安科瑞变电站电力监控系统的应用
摘 要:在电力系统的运行过程中,变电站作为整个电力系统的核心,在保证电力系统可靠的运行方面起着至关重要的作用,基于此需对变电站监控系统的特点进行分析,结合变电站监控系统的功能需求,对变电站电力监控系…...
Tapdata 和 Databend 数仓数据同步实战
作者:韩山杰https://github.com/hantmacDatabend Cloud 研发工程师基础架构在云计算时代也发生着翻天地覆的变化,对于业务的支持变成了如何能利用好云资源实现降本增效,同时更好的支撑业务也成为新时代技术人员的挑战。 本篇文章通过…...
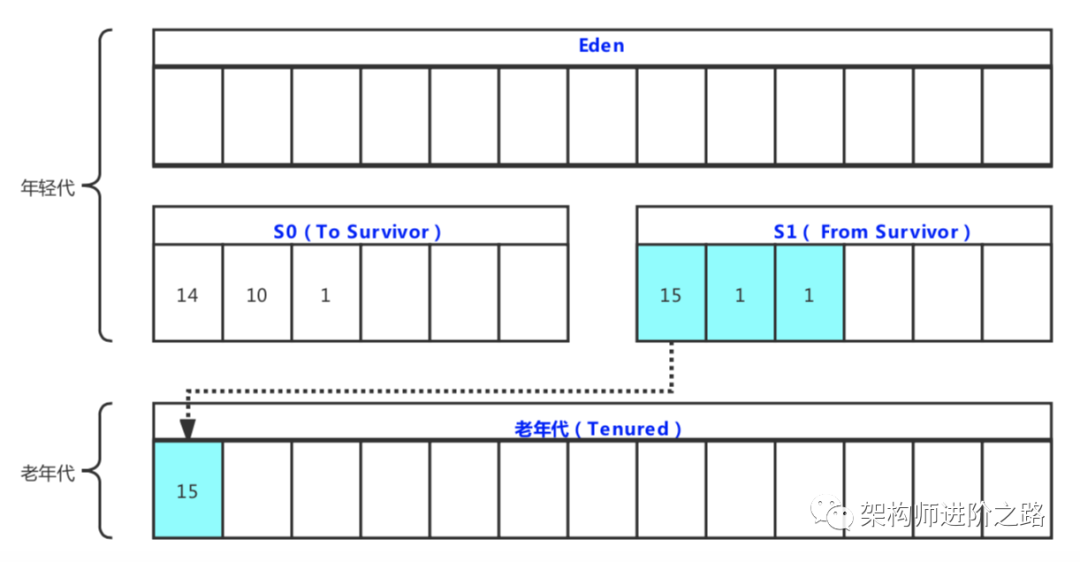
单核CPU, 1G内存,也能做JVM调优吗?
最近,笔者的技术群里有人问了一个有趣的技术话题:单核CPU, 1G内存的超低配机器,怎么做JVM调优?这实际上是两个问题。单核CPU的超低配机器,怎么充分利用CPU?单核CPU, 1G内存的超低配机器,怎么做J…...

《计算机应用研究》投稿经历和时间节点
记录四川计算机研究院《计算机应用研究》期刊投稿经历和时间节点。 日期状态周期2022.11.09上传稿件当天显示编辑部已接收稿件,开始初审2022.11.09 – 2022.11.15初审6天2022.11.15 – 2022.12.21外审36天2022.12.21收到退修意见(邮件形式)编…...
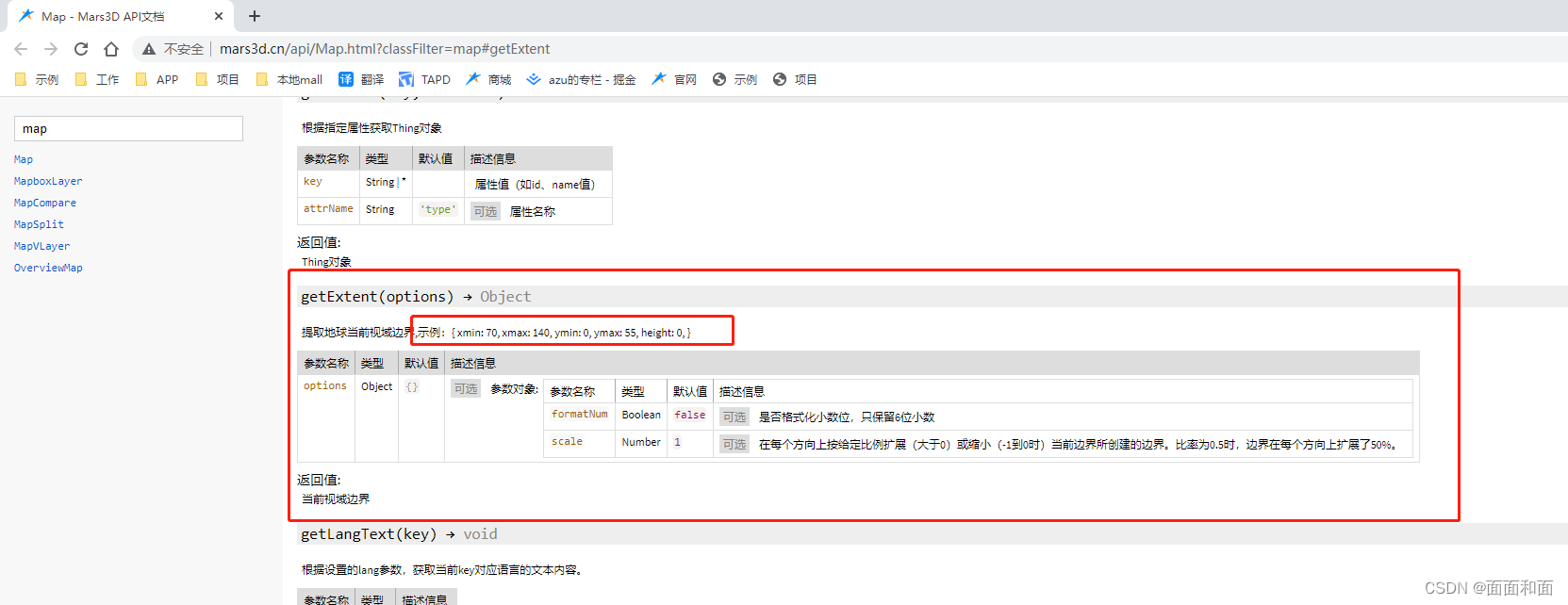
mars3d获取视窗的范围
期望效果 :1.我现在想获取到当前视窗的地图范围,请问有什么⽅法可以拿到吗 2.⽐如当前视窗地图范围的边界点,每个边界点的经纬度 回复:1.mars3d的API⽂档中有相关的⽅法 2.具体使⽤可以参考⽂档地址:http://mars3d.cn/api/Map.htm…...
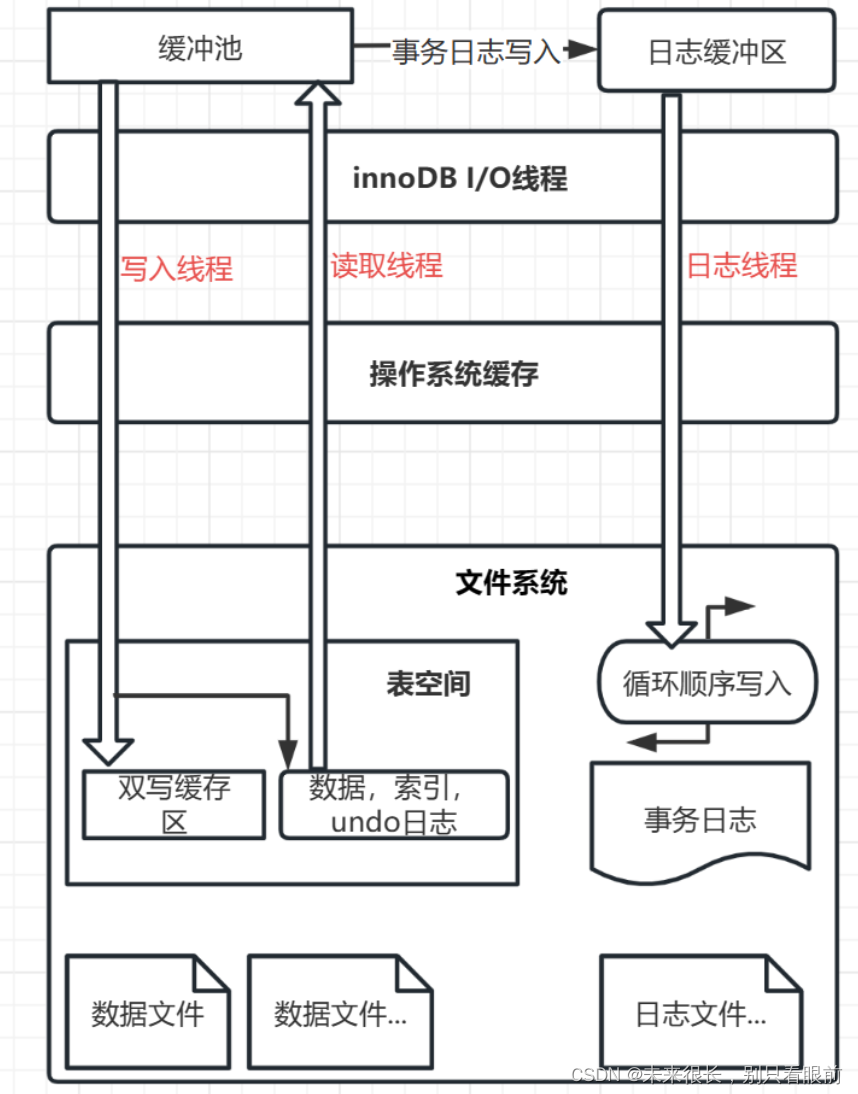
《高性能MySQL》读书笔记(上)
目录 MySQL的架构 MySQL中的锁 MySQL中的事务 事务特性 隔离级别 事务日志 多版本并发控制MVCC 影响MySQL性能的物理因素 InnoDB缓冲池 MySQL常用的数据类型以及优化 字符串类型 日期和时间类型 数据标识符 MySQL的架构 默认情况下,每个客户端连接都…...

05-代理模式
代理模式 代理模式使用代理对象来代替真实对象的访问,在不修改原有对象的前提下,提供额外的操作,扩展目标对象的功能。代理模式分为静态代理和动态代理。 静态代理 手动为目标对象中的方法进行增强,通过实现相同接口重写方法进…...

RocketMQ源码分析之消费队列、Index索引文件存储结构与存储机制-上篇
RocketMQ 存储基础回顾: 源码分析RocketMQ之CommitLog消息存储机制 本文主要从源码的角度分析 Rocketmq 消费队列 ConsumeQueue 物理文件的构建与存储结构,同时分析 RocketMQ 索引文件IndexFile 文件的存储原理、存储格式以及检索方式。RocketMQ 的存储…...
基于Java的浏览器的设计与实现毕业设计
技术:Java等摘要:当今世界是一个以计算机网络为核心的信息时代,互联网为人们快速获取、发布和传递信息提供了便捷,而浏览器作为互联网上查找信息的重要工具,给人们提供了巨大而又宝贵的信息财富,受到了大家…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

跨链模式:多链互操作架构与性能扩展方案
跨链模式:多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈:模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展(H2Cross架构): 适配层…...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...

全志A40i android7.1 调试信息打印串口由uart0改为uart3
一,概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本:2014.07; Kernel版本:Linux-3.10; 二,Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01),并让boo…...

AI书签管理工具开发全记录(十九):嵌入资源处理
1.前言 📝 在上一篇文章中,我们完成了书签的导入导出功能。本篇文章我们研究如何处理嵌入资源,方便后续将资源打包到一个可执行文件中。 2.embed介绍 🎯 Go 1.16 引入了革命性的 embed 包,彻底改变了静态资源管理的…...
