三数之和[中等]
优质博文:IT-BLOG-CN
一、题目
给你一个整数数组nums,判断是否存在三元组[nums[i], nums[j], nums[k]]满足i != j、i != k且j != k,同时还满足nums[i] + nums[j] + nums[k] == 0。请你返回所有和为0且不重复的三元组。
注意:答案中不可以包含重复的三元组。
示例 1:
输入:nums = [-1,0,1,2,-1,-4]
输出:[[-1,-1,2],[-1,0,1]]
解释:
nums[0] + nums[1] + nums[2] = (-1) + 0 + 1 = 0
nums[1] + nums[2] + nums[4] = 0 + 1 + (-1) = 0
nums[0] + nums[3] + nums[4] = (-1) + 2 + (-1) = 0
不同的三元组是[-1,0,1]和[-1,-1,2]
注意,输出的顺序和三元组的顺序并不重要。
示例 2:
输入:nums = [0,1,1]
输出:[]
解释:唯一可能的三元组和不为0
示例 3:
输入:nums = [0,0,0]
输出:[[0,0,0]]
解释:唯一可能的三元组和为0
3 <= nums.length <= 3000
-105 <= nums[i] <= 105
二、代码
排序 + 双指针: 题目中要求找到所有「不重复」且和为0的三元组,这个「不重复」的要求使得我们无法简单地使用三重循环枚举所有的三元组。这是因为在最坏的情况下,数组中的元素全部为0,即[0,0,0,0,0]任意一个三元组的和都为0。如果我们直接使用三重循环枚举三元组,会得到O(N3)个满足题目要求的三元组(其中N是数组的长度)时间复杂度至少为O(N3)。在这之后,我们还需要使用哈希表进行去重操作,得到不包含重复三元组的最终答案,又消耗了大量的空间。这个做法的时间复杂度和空间复杂度都很高,因此我们要换一种思路来考虑这个问题。
「不重复」的本质是什么?我们保持三重循环的大框架不变,只需要保证:第二重循环枚举到的元素不小于当前第一重循环枚举到的元素;第三重循环枚举到的元素不小于当前第二重循环枚举到的元素。
也就是说,我们枚举的三元组(a,b,c)满足a≤b≤ca,保证了只有(a,b,c)这个顺序会被枚举到,而(b,a,c)(c,b,a)等等这些不会,这样就减少了重复。要实现这一点,我们可以将数组中的元素从小到大进行排序,随后使用普通的三重循环就可以满足上面的要求。同时,对于每一重循环而言,相邻两次枚举的元素不能相同,否则也会造成重复。举个例子,如果排完序的数组为[]1,2,2,2,4]
nums.sort()
for first = 0 .. n-1// 只有和上一次枚举的元素不相同,我们才会进行枚举if first == 0 or nums[first] != nums[first-1] thenfor second = first+1 .. n-1if second == first+1 or nums[second] != nums[second-1] thenfor third = second+1 .. n-1if third == second+1 or nums[third] != nums[third-1] then// 判断是否有 a+b+c==0check(first, second, third)
这种方法的时间复杂度仍然为O(N3),毕竟我们还是没有跳出三重循环的大框架。然而它是很容易继续优化的,可以发现,如果我们固定了前两重循环枚举到的元素a和b,那么只有唯一的c满足a+b+c=0。当第二重循环往后枚举一个元素b时,由于b′>b,那么满足a+b′+c′=0的c′一定有c′<c,即c′在数组中一定出现在c的左侧。也就是说,我们可以从小到大枚举b,同时从大到小枚举c,即第二重循环和第三重循环实际上是并列的关系。
有了这样的发现,我们就可以保持第二重循环不变,而将第三重循环变成一个从数组最右端开始向左移动的指针,从而得到下面的伪代码:
nums.sort()
for first = 0 .. n-1if first == 0 or nums[first] != nums[first-1] then// 第三重循环对应的指针third = n-1for second = first+1 .. n-1if second == first+1 or nums[second] != nums[second-1] then// 向左移动指针,直到 a+b+c 不大于 0while nums[first]+nums[second]+nums[third] > 0third = third-1// 判断是否有 a+b+c==0check(first, second, third)
这个方法就是我们常说的「双指针」,当我们需要枚举数组中的两个元素时,如果我们发现随着第一个元素的递增,第二个元素是递减的,那么就可以使用双指针的方法,将枚举的时间复杂度从O(N2)减少至O(N)。为什么是O(N)呢?这是因为在枚举的过程每一步中,「左指针」会向右移动一个位置(也就是题目中的b),而「右指针」会向左移动若干个位置,这个与数组的元素有关,但我们知道它一共会移动的位置数为O(N),均摊下来,每次也向左移动一个位置,因此时间复杂度为O(N)。
注意到我们的伪代码中还有第一重循环,时间复杂度为O(N),因此枚举的总时间复杂度为O(N2)。由于排序的时间复杂度为O(NlogN),在渐进意义下小于前者,因此算法的总时间复杂度为O(N2)。
上述的伪代码中还有一些细节需要补充,例如我们需要保持左指针一直在右指针的左侧(即满足b≤c),具体可以参考下面的代码,均给出了详细的注释。
class Solution {public List<List<Integer>> threeSum(int[] nums) {//思想:1、先对 nums 进行排序// 2、先确定第一层循环,通过 0 - nums[x] 得到第二层和第三层的和// 3、将第二层和第三层汇总为一层,left = i + 1; right = nums.length - 1; 进行双指针移动,计算和,如果相等,加入队列,并继续移动指针,直到不满足 left < rightint left = 0, right = 0, size = 0;List<List<Integer>> res = new ArrayList();Arrays.sort(nums);for(int i = 0; i < nums.length; i++) {if (i > 0 && i < nums.length && nums[i] == nums[i-1]) {continue;}// i 发生变化之后,left 和 right 指针都需要发生变化。 第一次将right定义再外部,导致bugleft = i + 1;right = nums.length - 1;int tar = -nums[i];while(left < right) {if (nums[left] + nums[right] == tar) {List<Integer> temp = Arrays.asList(nums[i], nums[left], nums[right]);res.add(temp);// 数据去重while(left < right && nums[left] == nums[left + 1]) {++left;}while(right > left && nums[right] == nums[right - 1]) {--right;}++left;--right;} else if(nums[left] + nums[right] < tar){++left;} else {--right;}}}return res;}
}
时间复杂度: O(N2)其中N是数组nums的长度。
时间复杂度: O(N2),其中N是数组nums的长度。
相关文章:

三数之和[中等]
优质博文:IT-BLOG-CN 一、题目 给你一个整数数组nums,判断是否存在三元组[nums[i], nums[j], nums[k]]满足i ! j、i ! k且j ! k,同时还满足nums[i] nums[j] nums[k] 0。请你返回所有和为0且不重复的三元组。 注意:答案中不可以…...

基于天牛须优化的BP神经网络(分类应用) - 附代码
基于天牛须优化的BP神经网络(分类应用) - 附代码 文章目录 基于天牛须优化的BP神经网络(分类应用) - 附代码1.鸢尾花iris数据介绍2.数据集整理3.天牛须优化BP神经网络3.1 BP神经网络参数设置3.2 天牛须算法应用 4.测试结果&#x…...

渗透波菜网站
免责声明 本文发布的工具和脚本,仅用作测试和学习研究,禁止用于商业用途,不能保证其合法性,准确性,完整性和有效性,请根据情况自行判断。如果任何单位或个人认为该项目的脚本可能涉嫌侵犯其权利,…...

Spring Boot:Dao层-实例介绍
目录 Dao层的作用Dao层的特点与 Service 层和 Controller 层的关系实例介绍MenuDaoOperatorLogDaoRoleDaoUserDao四个文件的共同点引用的包使用Repository注解继承JpaRepository接口接口的实体类的主键类型使用 Query()注解 Dao层的作用 负责与数据库进行交互,主要…...

接口测试入门:深入理解接口测试!
很多人会谈论接口测试。到底什么是接口测试?如何进行接口测试?这篇文章会帮到你。 一、前端和后端 在谈论接口测试之前,让我们先明确前端和后端这两个概念。 前端是我们在网页或移动应用程序中看到的页面,它由 HTML 和 CSS 编写…...
Redis微服务架构
Redis微服务架构 缓存设计 缓存穿透 缓存穿透是指查询一个根本不存在的数据,缓存层和存储层都不会命中,通常出于容错的考虑,如果从存储层查不到数据则不写入缓层。 缓存穿透将导致不存在的数据每次请求都要到存储层去查询,失去…...

【C++】 局部对象,引用返回
1、new 关键字 会在堆内申请空间,如果仅仅是普通调用构造函数,不会在堆内开辟空间。 2、函数调用会形成栈帧,进行压栈操作,函数调用结束,会进行弹栈。 函数内的局部对象,会随着弹栈,而被销毁(…...

线性代数中涉及到的matlab命令-第二章:矩阵及其运算
目录 1,矩阵定义 2,矩阵的运算 3,方阵的行列式和伴随矩阵 4,矩阵的逆 5,克莱默法则 6,矩阵分块 1,矩阵定义 矩阵与行列式的区别: (1)形式上行列式…...

计算机毕业设计选什么题目好?springboot 美食推荐系统
✍✍计算机编程指导师 ⭐⭐个人介绍:自己非常喜欢研究技术问题!专业做Java、Python、微信小程序、安卓、大数据、爬虫、Golang、大屏等实战项目。 ⛽⛽实战项目:有源码或者技术上的问题欢迎在评论区一起讨论交流! ⚡⚡ Java实战 |…...
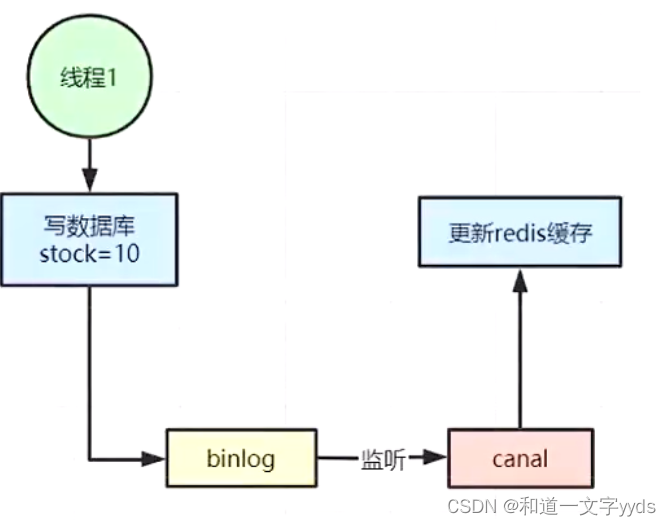
爆肝整理,Jmeter接口性能测试-跨线程调用变量实操(超详细)
目录:导读 前言一、Python编程入门到精通二、接口自动化项目实战三、Web自动化项目实战四、App自动化项目实战五、一线大厂简历六、测试开发DevOps体系七、常用自动化测试工具八、JMeter性能测试九、总结(尾部小惊喜) 前言 1、Jmeter中线程运…...
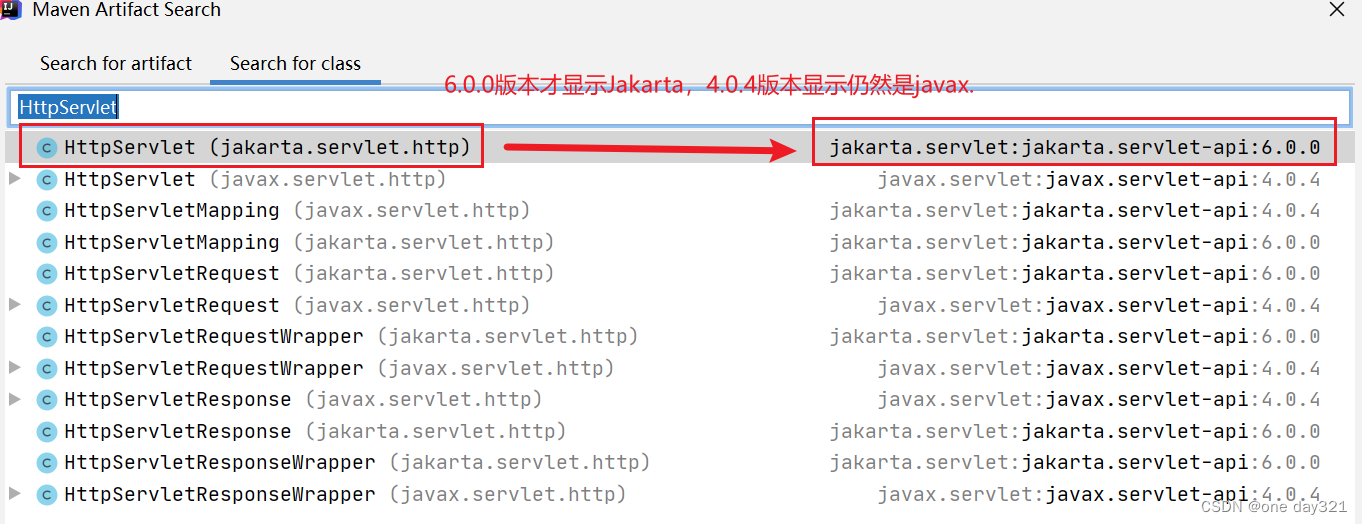
Maven导入程序包jakarta.servlet,但显示不存在
使用前提:(Tomcat10版本)已知tomcat10版本之后,使用jakart.servlet。而tomcat9以及之前使用javax.servlet。 问题描述:在maven仓库有导入了Jakarta程序包,但是界面仍然显示是javax。(下图&…...
es6(二)——常用es6说明
ES6的系列文章目录 es6(一)——var和let和const的区别 文章目录 ES6的系列文章目录一、变量的结构赋值1.数组的结构赋值2.对象的结构赋值 二、模板字符串三、扩展运算符1.字符串的使用2.数组的使用 四、箭头函数1.普通函数的定义2.箭头函数的定义3.箭头…...
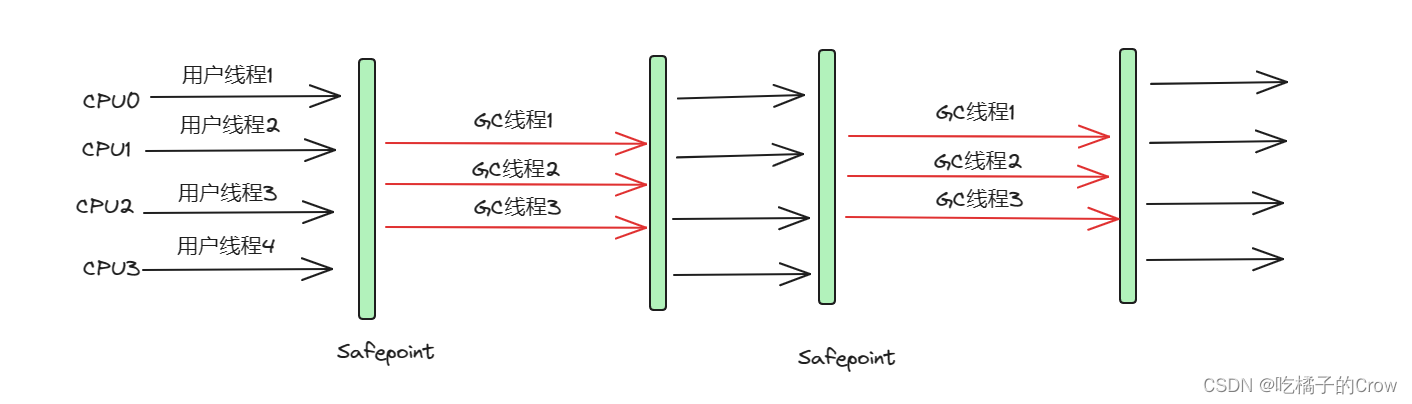
经典垃圾回收器
1.各垃圾回收器之间的配合使用关系 2.垃圾回收器的种类 2.1 Serial收集器(默认新生代收集器) Serial收集器是历史最悠久的收集器,曾经是新生代收集器的唯一选择,它是一个单线程工作的收集器,其“单线程”的意义不仅仅…...

台达DOP-B07S410触摸屏出现HMI no response无法上传的解决办法
台达DOP-B07S410触摸屏出现HMI no response无法上传的解决办法 台达触摸屏(B07S410)在上载程序时(显示No response from HMI)我以前的电脑是WIN7的,从来没出现过这样的问题,现在换成win10的,怎么都不行,(USB显示是一个大容量存储)换一台电脑(win10)有些行,有些不行…...

[资源推荐] 复旦大学张奇老师科研分享
刷B站的时候首页给我推了这个:【直播回放】复旦大学张奇教授亲授:人工智能领域顶会论文的发表指南先前也散漫地读了些许论文,但没有在一些宏观的方法论下去训练,读的时候能感觉出一些科研的套路,论文写作的套路&#x…...

C++数位动态规划算法:统计整数数目
题目 给你两个数字字符串 num1 和 num2 ,以及两个整数 max_sum 和 min_sum 。如果一个整数 x 满足以下条件,我们称它是一个好整数: num1 < x < num2 min_sum < digit_sum(x) < max_sum. 请你返回好整数的数目。答案可能很大&…...

ip 网段设置 --chatGPT
问:host all all 127.0.0.1/32 scram-sha-256 里的 127.0.0.1/32 是什么含义 ,要指定某个呢 gpt: 在 PostgreSQL 的 pg_hba.conf 文件中,127.0.0.1/32 是一个用于定义访问控制规则的CIDR(无类域间路由)标记࿰…...

使用JMeter进行接口测试教程
安装 使用JMeter的前提需要安装JDK,需要JDK1.7以上版本目前在用的是JMeter5.2版本,大家可自行下载解压使用 运行 进入解压路径如E: \apache-jmeter-5.2\bin,双击jmeter.bat启动运行 启动后默认为英文版本,可通过Options – Cho…...

文本生成解码策略
解码策略 1. sample实现了怎样的功能 不是直接选择概率最大的token,而是根据多项式分布进行采样获得下一个token 这里的概率通过设置一些策略,进行处理。例如,解码最小长度(当长度小于该值的时候,eos的采样概率为0&am…...
华为数通方向HCIP-DataCom H12-831题库(单选题:221-240)
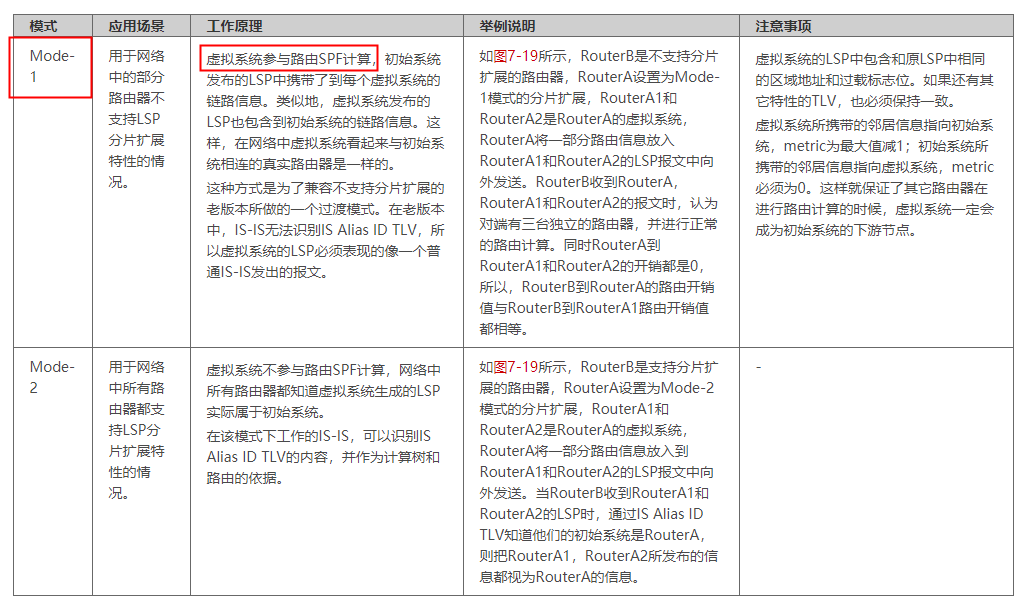
第221题 以下关于IS-IS的LSP分片功能的描述,正确的是哪一项? A、IS-IS的分片扩展功能的Mode-1模式,虚拟系统是需要参与路由SPF计算的 B、IS-IS的LSP分片功能,是用于让收到LSP分片报文的设备老化相关路由信息 C、IS-IS的分片扩展功能,是通过LSP报文中的LSPID实现的 D、IS-…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...

成都鼎讯硬核科技!雷达目标与干扰模拟器,以卓越性能制胜电磁频谱战
在现代战争中,电磁频谱已成为继陆、海、空、天之后的 “第五维战场”,雷达作为电磁频谱领域的关键装备,其干扰与抗干扰能力的较量,直接影响着战争的胜负走向。由成都鼎讯科技匠心打造的雷达目标与干扰模拟器,凭借数字射…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...

python执行测试用例,allure报乱码且未成功生成报告
allure执行测试用例时显示乱码:‘allure’ �����ڲ����ⲿ���Ҳ���ǿ�&am…...

React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store: 我们在使用异步的时候理应是要使用中间件的,但是configureStore 已经自动集成了 redux-thunk,注意action里面要返回函数 import { configureS…...

音视频——I2S 协议详解
I2S 协议详解 I2S (Inter-IC Sound) 协议是一种串行总线协议,专门用于在数字音频设备之间传输数字音频数据。它由飞利浦(Philips)公司开发,以其简单、高效和广泛的兼容性而闻名。 1. 信号线 I2S 协议通常使用三根或四根信号线&a…...
