【C++代码】最大二叉树,合并二叉树,二叉搜索树中的搜索,验证二叉搜索树--代码随想录
题目:最大二叉树
- 给定一个不重复的整数数组
nums。 最大二叉树 可以用下面的算法从nums递归地构建:- 创建一个根节点,其值为
nums中的最大值。 - 递归地在最大值 左边 的 子数组前缀上 构建左子树。
- 递归地在最大值 右边 的 子数组后缀上 构建右子树。
- 创建一个根节点,其值为
题解
-
构造树一般采用的是前序遍历,因为先构造中间节点,然后递归构造左子树和右子树。
-
确定递归函数的参数和返回值:参数传入的是存放元素的数组,返回该数组构造的二叉树的头结点,返回类型是指向节点的指针。
-
确定终止条件:题目中说了输入的数组大小一定是大于等于1的,所以我们不用考虑小于1的情况,那么当递归遍历的时候,如果传入的数组大小为1,说明遍历到了叶子节点了。那么应该定义一个新的节点,并把这个数组的数值赋给新的节点,然后返回这个节点。 这表示一个数组大小是1的时候,构造了一个新的节点,并返回。
-
确定单层递归的逻辑
- 先要找到数组中最大的值和对应的下标, 最大的值构造根节点,下标用来下一步分割数组。
- 最大值所在的下标左区间 构造左子树
- 最大值所在的下标右区间 构造右子树
-
class Solution { public:TreeNode* constructMaximumBinaryTree(vector<int>& nums) {TreeNode* temp_node = new TreeNode(0);if(nums.size()==1){temp_node->val=nums[0];return temp_node;}int maxval=0;int maxvalindex=0;for(int i=0;i<nums.size();i++){if(nums[i]>maxval){maxval=nums[i];maxvalindex=i;}}temp_node->val=maxval;if(maxvalindex>0){vector<int> leftvec(nums.begin(),nums.begin()+maxvalindex);temp_node->left=constructMaximumBinaryTree(leftvec);}if(maxvalindex<(nums.size()-1)){vector<int> rightvec(nums.begin()+maxvalindex+1,nums.end());temp_node->right=constructMaximumBinaryTree(rightvec);}return temp_node;} };
-
-
注意类似用数组构造二叉树的题目,每次分隔尽量不要定义新的数组,而是通过下标索引直接在原数组上操作,这样可以节约时间和空间上的开销。一般情况来说:如果让空节点(空指针)进入递归,就不加if,如果不让空节点进入递归,就加if限制一下, 终止条件也会相应的调整。
-
TreeNode* searsh(vector<int>& nums,int left,int right){if(left>=right){return nullptr;}int maxvalindex=left;for(int i=left+1;i<right;i++){if(nums[i]>nums[maxvalindex])maxvalindex=i;}TreeNode* root=new TreeNode(nums[maxvalindex]);root->left=searsh(nums,left,maxvalindex);root->right=searsh(nums,maxvalindex+1,right);return root;}
-
题目:合并二叉树
- 给你两棵二叉树:
root1和root2。当你将其中一棵覆盖到另一棵之上时,两棵树上的一些节点将会重叠(而另一些不会)。你需要将这两棵树合并成一棵新二叉树。合并的规则是:如果两个节点重叠,那么将这两个节点的值相加作为合并后节点的新值;否则,不为 null 的节点将直接作为新二叉树的节点。返回合并后的二叉树。注意: 合并过程必须从两个树的根节点开始。
题解
-
深度优先搜索:可以使用深度优先搜索合并两个二叉树。从根节点开始同时遍历两个二叉树,并将对应的节点进行合并。两个二叉树的对应节点可能存在以下三种情况,对于每种情况使用不同的合并方式。
- 如果两个二叉树的对应节点都为空,则合并后的二叉树的对应节点也为空;
- 如果两个二叉树的对应节点只有一个为空,则合并后的二叉树的对应节点为其中的非空节点;
- 如果两个二叉树的对应节点都不为空,则合并后的二叉树的对应节点的值为两个二叉树的对应节点的值之和,此时需要显性合并两个节点。
-
对一个节点进行合并之后,还要对该节点的左右子树分别进行合并。这是一个递归的过程。
-
class Solution { public:TreeNode* mergeTrees(TreeNode* root1, TreeNode* root2) {if(root1==nullptr){return root2;}if(root2==nullptr){return root1;}auto meged=new TreeNode(root1->val+root2->val);meged->left=mergeTrees(root1->left,root2->left);meged->right=mergeTrees(root1->right,root2->right);return meged;} }; -
时间复杂度:O(min(m,n)),其中 m 和 n 分别是两个二叉树的节点个数。对两个二叉树同时进行深度优先搜索,只有当两个二叉树中的对应节点都不为空时才会对该节点进行显性合并操作,因此被访问到的节点数不会超过较小的二叉树的节点数。
-
空间复杂度:O(min(m,n)),其中 m 和 n 分别是两个二叉树的节点个数。空间复杂度取决于递归调用的层数,递归调用的层数不会超过较小的二叉树的最大高度,最坏情况下,二叉树的高度等于节点数。
-
那么中序遍历也是可以的,代码如下:
-
class Solution { public:TreeNode* mergeTrees(TreeNode* t1, TreeNode* t2) {if (t1 == NULL) return t2; // 如果t1为空,合并之后就应该是t2if (t2 == NULL) return t1; // 如果t2为空,合并之后就应该是t1// 修改了t1的数值和结构t1->left = mergeTrees(t1->left, t2->left); // 左t1->val += t2->val; // 中t1->right = mergeTrees(t1->right, t2->right); // 右return t1;} };
-
-
后序遍历依然可以,代码如下:
-
class Solution { public:TreeNode* mergeTrees(TreeNode* t1, TreeNode* t2) {if (t1 == NULL) return t2; // 如果t1为空,合并之后就应该是t2if (t2 == NULL) return t1; // 如果t2为空,合并之后就应该是t1// 修改了t1的数值和结构t1->left = mergeTrees(t1->left, t2->left); // 左t1->right = mergeTrees(t1->right, t2->right); // 右t1->val += t2->val; // 中return t1;} };
-
题目:二叉搜索树中的搜索
- 给定二叉搜索树(BST)的根节点
root和一个整数值val。你需要在 BST 中找到节点值等于val的节点。 返回以该节点为根的子树。 如果节点不存在,则返回null。
题解
-
二叉搜索树是一个有序树:若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值;若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值;它的左、右子树也分别为二叉搜索树。
-
一提到二叉树遍历的迭代法,可能立刻想起使用栈来模拟深度遍历,使用队列来模拟广度遍历。对于二叉搜索树可就不一样了,因为二叉搜索树的特殊性,也就是节点的有序性,可以不使用辅助栈或者队列就可以写出迭代法。对于一般二叉树,递归过程中还有回溯的过程,例如走一个左方向的分支走到头了,那么要调头,在走右分支。而对于二叉搜索树,不需要回溯的过程,因为节点的有序性就帮我们确定了搜索的方向。
-
class Solution { public:TreeNode* searchBST(TreeNode* root, int val) {while(root!=nullptr){if(root->val>val){root=root->left;}else if(root->val<val){root=root->right;}else{return root;}}return nullptr;} }; -
确定递归函数的参数和返回值,递归函数的参数传入的就是根节点和要搜索的数值,返回的就是以这个搜索数值所在的节点。
-
确定终止条件,如果root为空,或者找到这个数值了,就返回root节点。
-
确定单层递归的逻辑,如果root->val > val,搜索左子树,如果root->val < val,就搜索右子树,最后如果都没有搜索到,就返回NULL。
-
class Solution { public:TreeNode* searchBST(TreeNode* root, int val) {if(root==nullptr||root->val==val){return root;}if(root->val>val){return searchBST(root->left,val);}if(root->val<val){return searchBST(root->right,val);}return nullptr;} };
题目:验证二叉搜索树
- 给你一个二叉树的根节点
root,判断其是否是一个有效的二叉搜索树。有效 二叉搜索树定义如下:节点的左子树只包含 小于 当前节点的数。节点的右子树只包含 大于 当前节点的数。所有左子树和右子树自身必须也是二叉搜索树。
题解
-
要知道中序遍历下,输出的二叉搜索树节点的数值是有序序列。有了这个特性,验证二叉搜索树,就相当于变成了判断一个序列是不是递增的了。
-
class Solution { public:vector<int> temp_vec;void trave(TreeNode *root){if(root==nullptr)return;trave(root->left);temp_vec.push_back(root->val);trave(root->right);}bool isValidBST(TreeNode* root) {temp_vec.clear();trave(root);for(int i=1;i<temp_vec.size();i++){if(temp_vec[i]<=temp_vec[i-1])return false;}return true;} }; -
可以用迭代法模拟二叉树中序遍历,
-
bool isValidBST(TreeNode* root) {stack<TreeNode*> st;TreeNode* cur=root;TreeNode* pre=nullptr;while(cur!=nullptr||!st.empty()){if(cur!=nullptr){st.push(cur);cur=cur->left;}else{cur=st.top();st.pop();if(pre!=nullptr&&cur->val<=pre->val){return false;}pre=cur;cur=cur->right;}}return true;}
相关文章:

【C++代码】最大二叉树,合并二叉树,二叉搜索树中的搜索,验证二叉搜索树--代码随想录
题目:最大二叉树 给定一个不重复的整数数组 nums 。 最大二叉树 可以用下面的算法从 nums 递归地构建: 创建一个根节点,其值为 nums 中的最大值。递归地在最大值 左边 的 子数组前缀上 构建左子树。递归地在最大值 右边 的 子数组后缀上 构建右子树。 …...
母婴用品会员商城小程序的作用是什么
随着政策放松,母婴行业相比以前迎来了更高的发展空间,由于可以与多个行业连接,因此市场规模也是连年上升,母婴用品是行业重要的分支,近些年从业商家连年增加,但在实际经营中,商家所遇经营痛点也…...

c++初阶--内存管理
目录 c/c 内存分布c内存管理方式new/delete操作内置类型new和delete操作自定义类型 operator new与operator delete函数new和delete的实现原理内置类型自定义类型 malloc/free和new/delete的区别内存泄露什么是内存泄漏,内存泄露的危害如何避免内存泄漏 在c语言中我…...
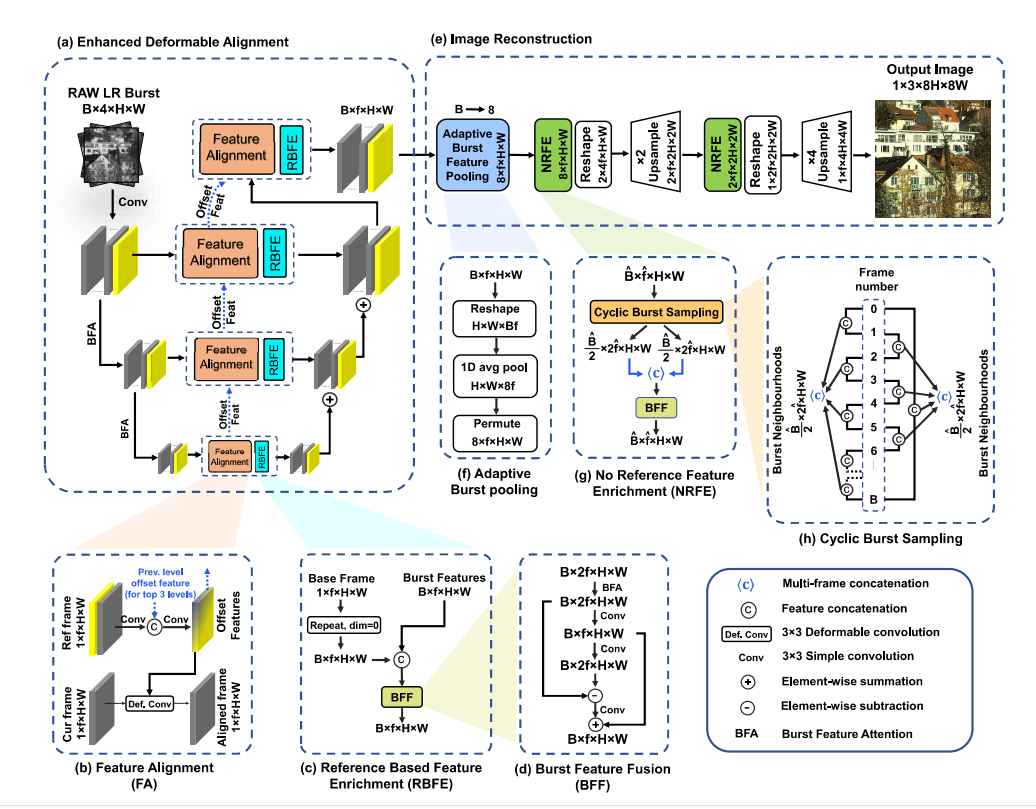
Burstormer论文阅读笔记
这是CVPR2023的一篇连拍图像修复和增强的论文,一作是阿联酋的默罕默德 本 扎耶得人工智能大学,二作是旷视科技。这些作者和CVPR2022的一篇BIPNet,同样是做连拍图像修复和增强的,是同一批。也就是说同一个方向,22年中了…...
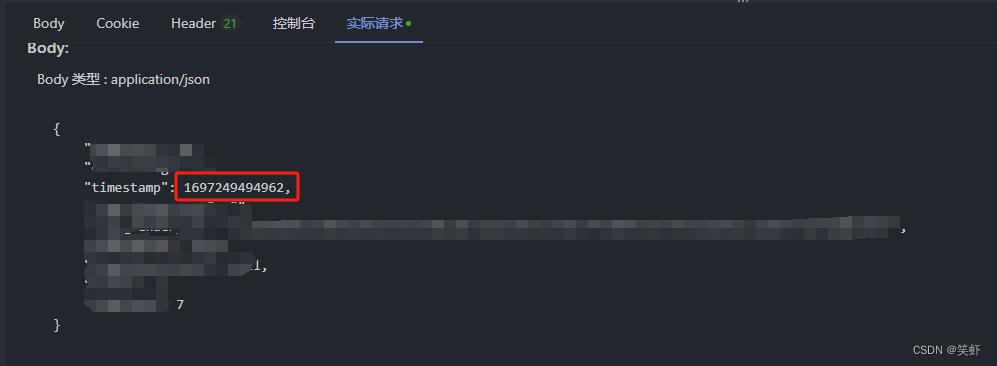
Apifox 学习笔记 - 前置操作之:动态更新请求体中的时间戳
Apifox 学习笔记 - 前置操作之:动态更新请求体中的时间戳 1. 在前置操作中添加一个:自定义脚本或公共脚本2. 定义我们所需的环境变量。3. 在请求参数中使用【时间戳】4. 检验参考资料 1. 在前置操作中添加一个:自定义脚本或公共脚本 2. 定义我…...
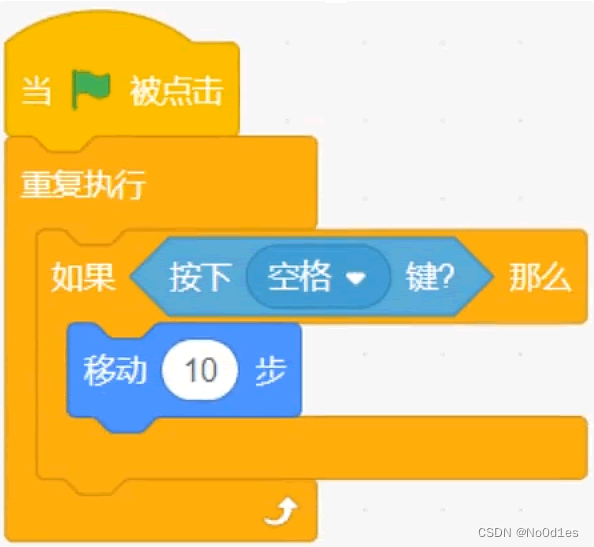
2023年9月 青少年软件编程等级考试Scratch二级真题
202309 青少年软件编程等级考试Scratch二级真题(电子学会等级考试) 试卷总分数:100分 试卷及格分:60 分 考试时长:60 分钟 第 1 题 点击绿旗,运行程序后,舞台上的图形是?( ) A:画…...

12.验证码以及付费代理
文章目录 一、验证码的处理1、验证码概述1、2 什么是图片验证码?1、2 验证码的作用1、3 图片验证码使用场景1、4 图片验证码的处理方案 2、图片在网页页面中的形式2、1 如何进行图片形式的转化 3、打码平台 二、代理的使用2、1 付费代理2、1、1 找付费代理服务站点2…...
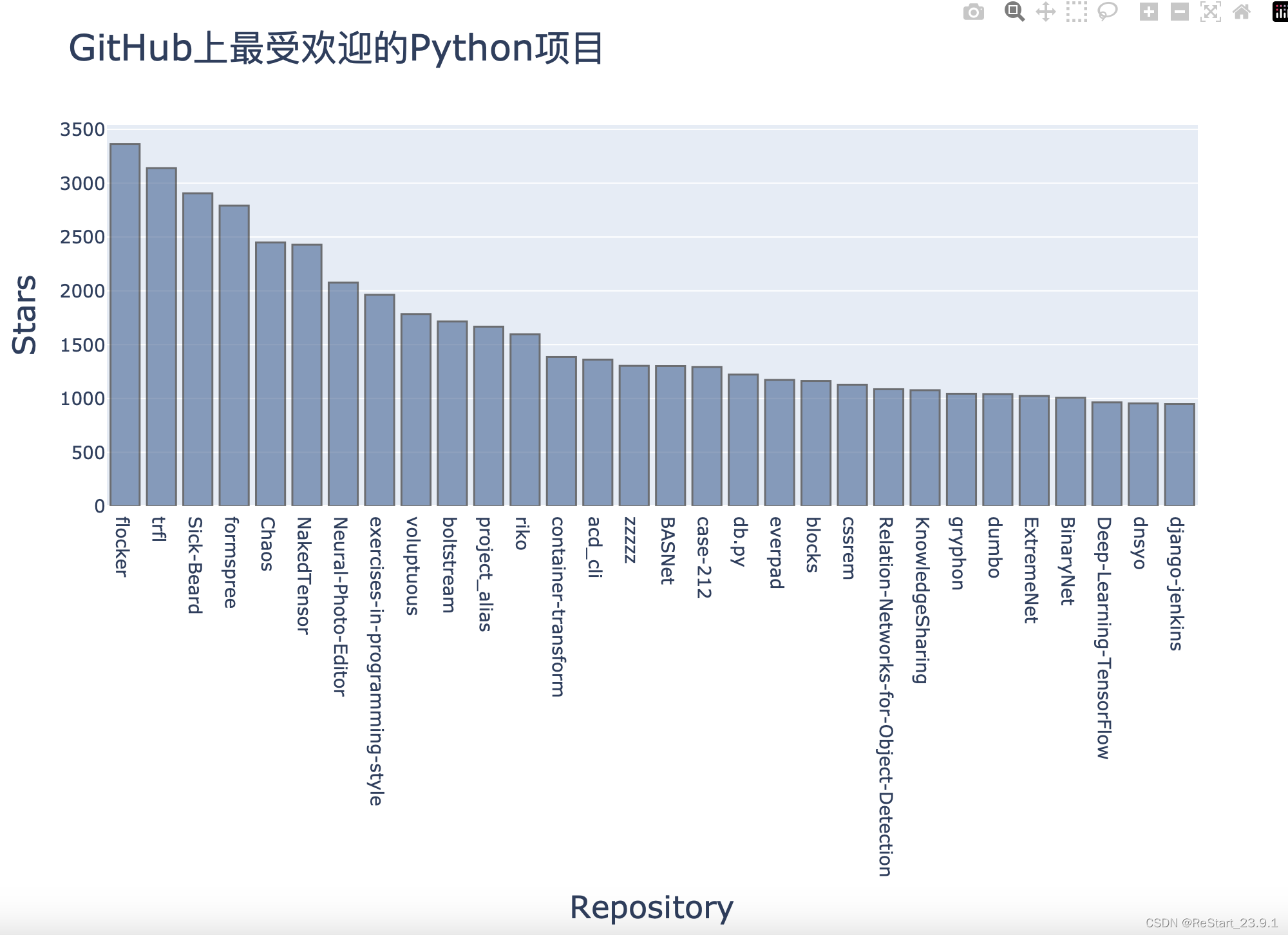
使用Plotly可视化
显示项目受欢迎程度 改进图表 设置颜色,字体...
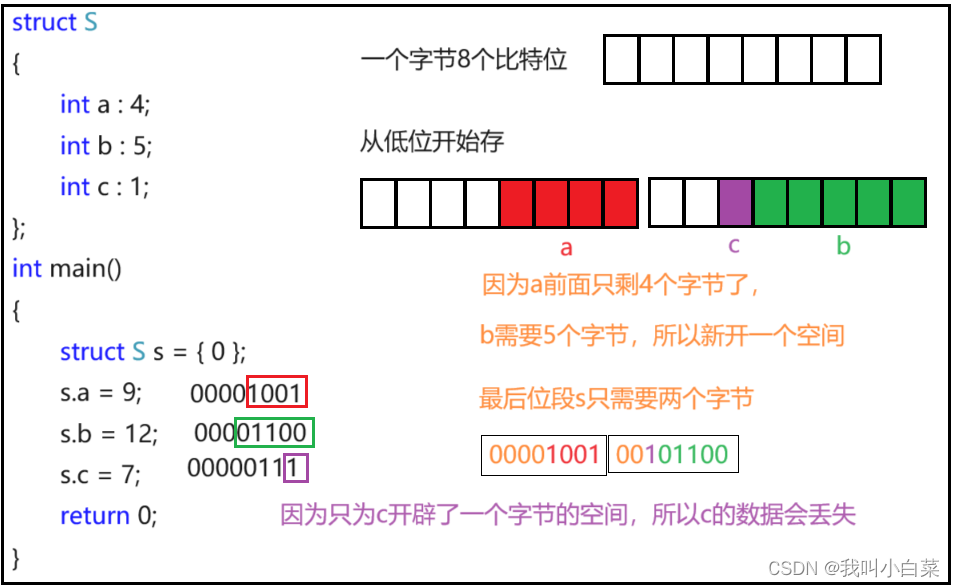
【C语言】结构体、位段、枚举、联合(共用体)
结构体 结构:一些值的集合,这些值称为成员变量。结构体的每个成员可以是不同类型的变量; 结构体声明:struct是结构体关键字,结构体声明不能省略struct; 匿名结构体:只能在声明结构体的时候声…...
“Python+”集成技术高光谱遥感数据处理与机器学习深度应用
涵盖高光谱遥感数据处理的基础、python开发基础、机器学习和应用实践。重点解释高光谱数据处理所涉及的基本概念和理论,旨在帮助学员深入理解科学原理。结合Python编程工具,专注于解决高光谱数据读取、数据预处理、高光谱数据机器学习等技术难题…...

Excel 转为 PDF,PNG,HTML等文件
1.安装 Spire.XLS for Java,下载jar包 下载地址 2.引入方式一(我这里这种方式一直无法引入,都是失败,所以用的方式二) <repositories><repository><id>com.e-iceblue</id><name>e-iceblue</na…...
docker中使用GPU+rocksdb
配置环境 delldell-Precision-3630-Tower ~ lsb_release -a No LSB modules are available. Distributor ID: Ubuntu Description: Ubuntu 20.04.6 LTS Release: 20.04 Codename: focaldelldell-Precision-3630-Tower ~ nvcc --version nvcc: NVIDIA (R) Cuda comp…...
好用的跨平台同步笔记工具,手机和电脑可同步的笔记工具
在这个快节奏的工作环境中,每个人都在寻找一种方便又高效的方式来记录工作笔记。记录工作笔记可以帮助大家统计工作进展,了解工作进程,而如果工作中常在一个地方办公,直接选择电脑或者手机中笔记工具来记录即可,但是对…...

【Python 千题 —— 基础篇】浮点数转换为整数
题目描述 题目描述 整数转换为浮点数。 输入描述 输入一个整数。 输出描述 程序将整数转换为浮点数并输出。 示例 示例 ① 2输出: 2.0代码讲解 下面是本题的代码: # 描述: 整数转换为浮点数。 # 输入: 输入一个整数。 # 输出: 程序将整数转换…...

金融科技论文D部分
总结 以每周为例, 动量因子定义每种货币为前一周的回报率 价值因子定义为当前市值与其区块链中过去 7 天平均链上交易价值 利差因子定义为前 7 天硬币发行总量的负数除以在7天期限开始时未偿还的硬币量。 因素定义 为了避免过拟合,我们试图定义每一…...

Apache Tomcat下载安装配置使用超详细
下载安装 tomcat官网 在此我们以Tomcat 9.0.81为例,点击下载压缩包,解压到自己的文件夹。 tar.gz是linux操作系统下的安装版本。zip是windows系统下的压缩版本。Windows Service Installer是windows操作系统下的exe安装版本。 检查是否配置JDK 1.…...
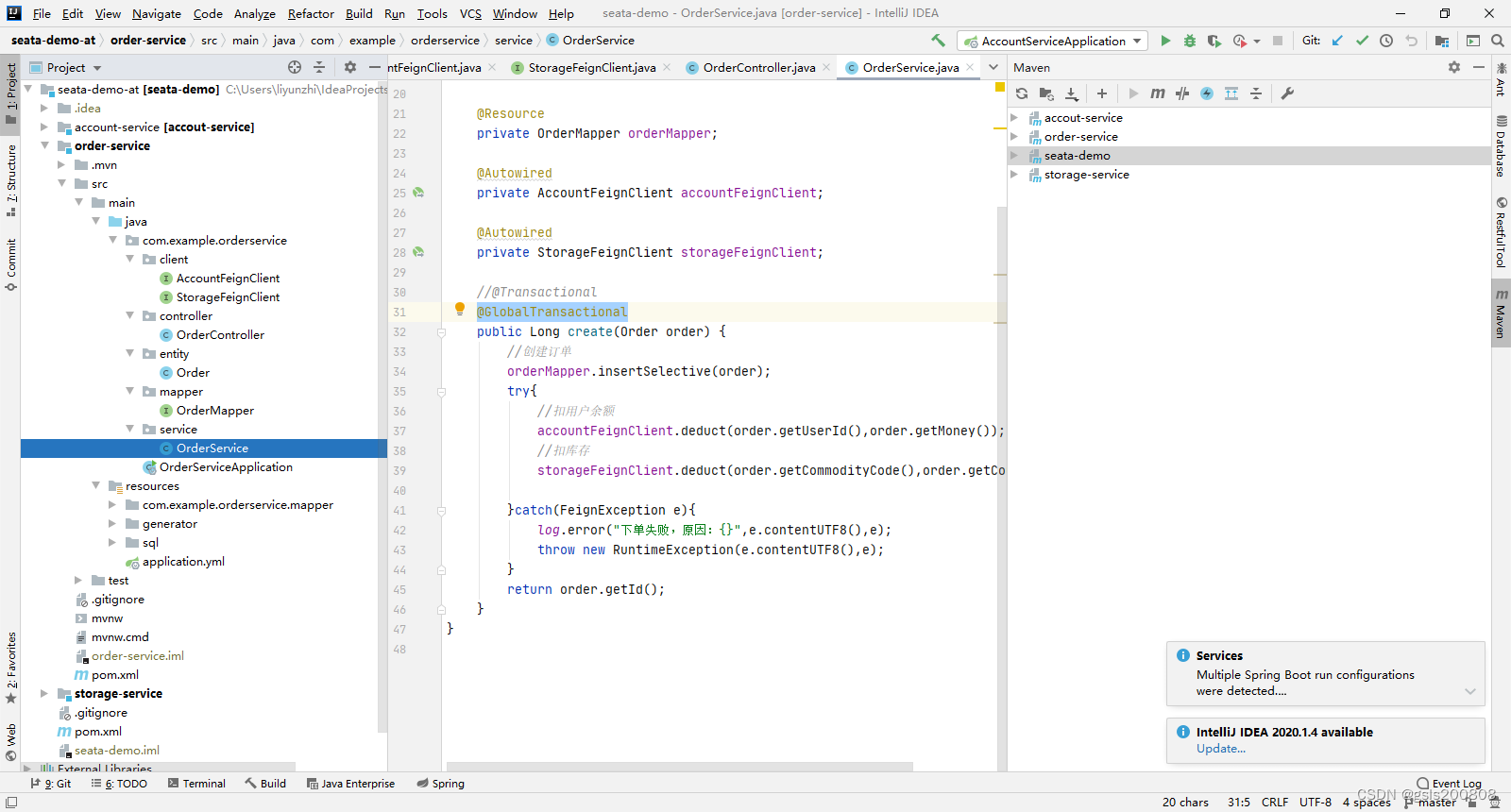
基于Seata的分布式事务方案
在Seata中,有4种分布式事务实现方案 XA、AT、TCC、Saga 其中XA利用了数据库的分布式事务特性,AT相当于框架去控制事务回滚。TCC手写三个方法,saga手写两个方法。 AT的性能和编写比较折中,是最常用的一种。TCC一些视频教程中介绍…...
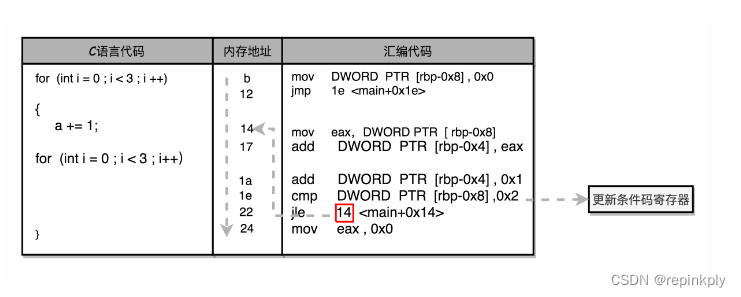
指令跳转:原来if...else就是goto
目录 CPU 是如何执行指令的? 从 if…else 来看程序的执行和跳转 如何通过 if…else 和 goto 来实现循环? 小结 你平时写的程序中,肯定不只有 int a 1 这样最最简单的代码或者指令。我们总是要用到 if…else 这样的条件判断语句、while 和…...
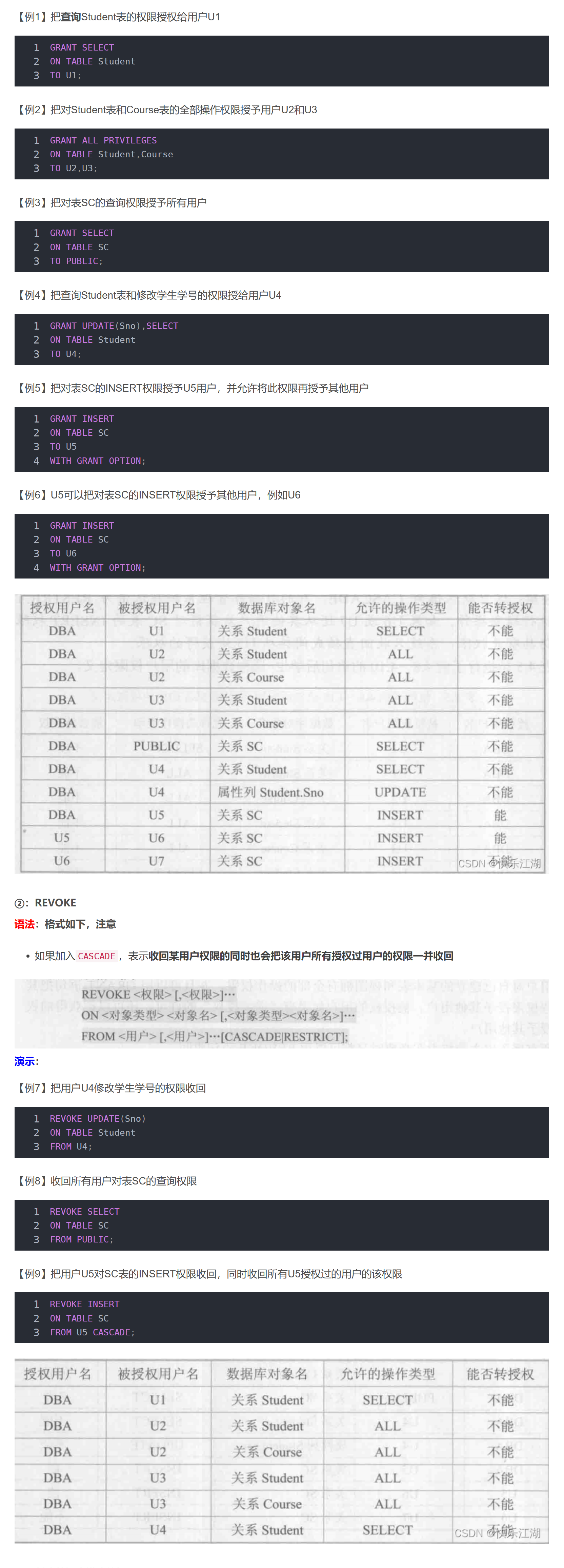
【数据库系统概论】第四章数据库安全性
数据库的安全性:保护数据库以防止不合法使用所造成的数据泄露、更改或破坏 grant和revoke语法...

如何正确的关闭Redis服务器
Redis官方原生版本是在Linux平台上开发和测试的,但是大多数初学者都是使用Windows系统来学习如何开发的。因此,官方提供了一个叫做“Microsoft Open Tech Redis”的项目,该项目专门为Windows平台提供了一个官方支持的Redis版本,但…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

vscode(仍待补充)
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh? debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...

2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...
