【计算机组成体系结构】电路基本原理与加法器设计

一、算术逻辑单元—ALU

 

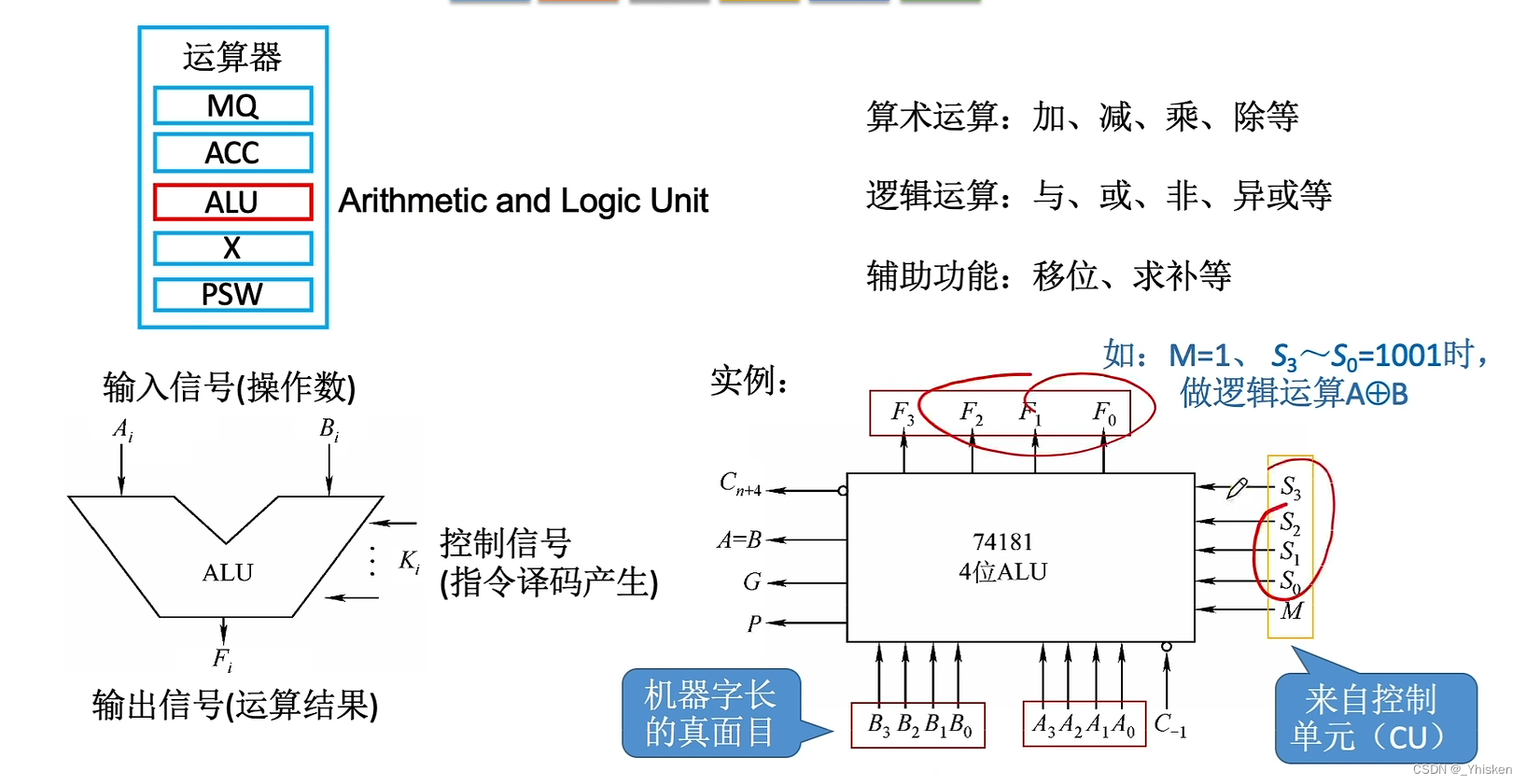
1.基本的逻辑运算（1bit的运算） 

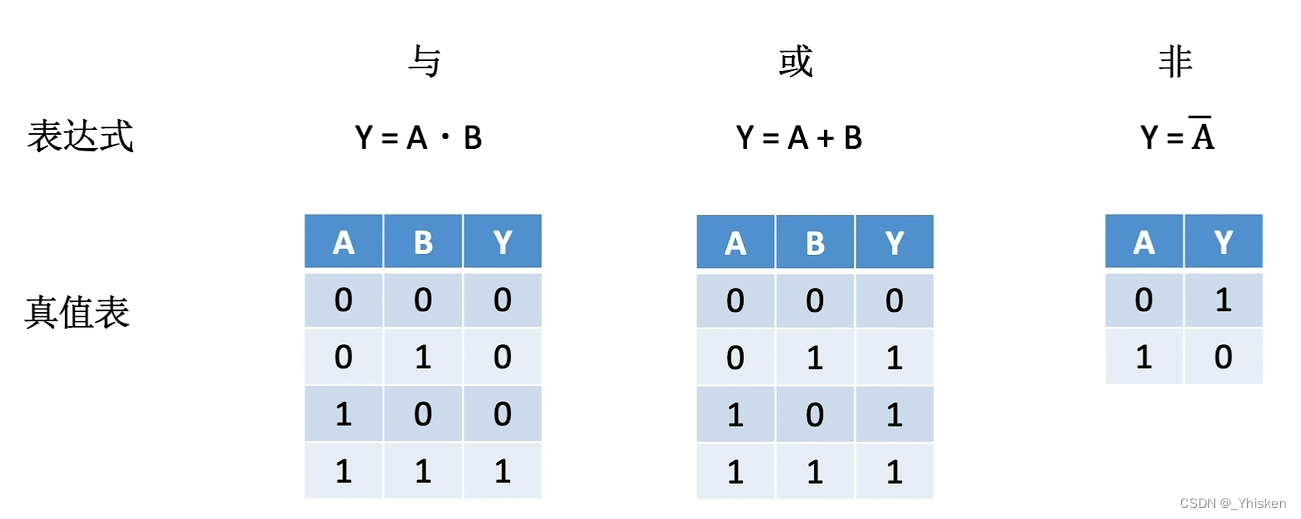
基本逻辑运算分为，与、或、非。大家应该很熟悉了，与：全1为1，否则为0。或：全0为0，否则为1。非：取反。三个基本的逻辑运算可以由对应的门电路实现。（与门，或门，非门）

这里以上图的与门为例，若输入端A为高电压5V，表示1，输入端B电压为1V，表示0。则输出端Y输出的是低电压1V，表示0。由此完成电信号表示的逻辑运算。或门同理。

(1)“与”和“或”的优先级

在加法乘法中，我们知道乘法的优先级是高于加法的。那么在逻辑运算中如果，与或运算同时出现，“与”运算的优先级是高于“或”运算的。

如“A·B + C·D”应该先计算A·B和C·D，再计算A·B + C·D。

(2)分配律和结合律

与或操作同时满足分配律，和结合律，同时类比加法和乘法的关系。

分配律——A·(C+D)= A·C+A·D 

结合律——A·B·C=A·(B·C)

结合律——A+B+C=A+(B+C)

同一种运算的两种电路实现

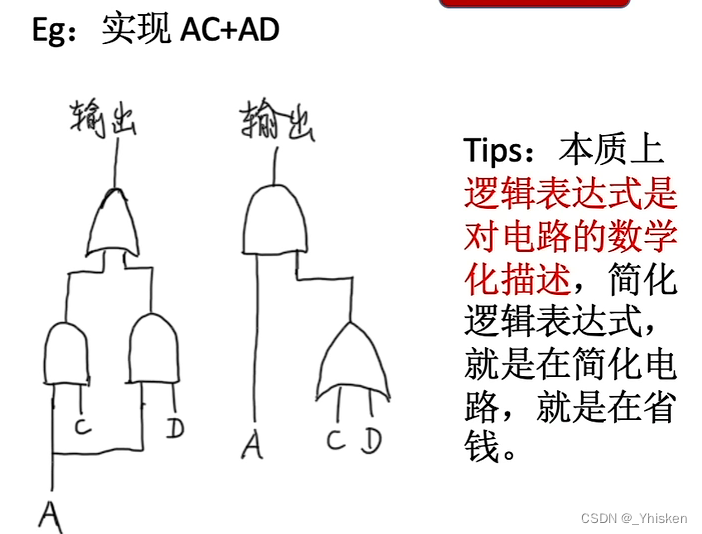
这些定律的用处，以上面的 A·C + A·D 为例，如果保持原来的式子不变，我们可以用两个与门和一个或门实现(如上图左)。但如果用分配律变换为A·(C+D)，我们仅仅需要一个与门和一个或门就可以实现相同的运算(如上图右)，并且会节省硬件成本。

2.复合逻辑（1bit的运算） 

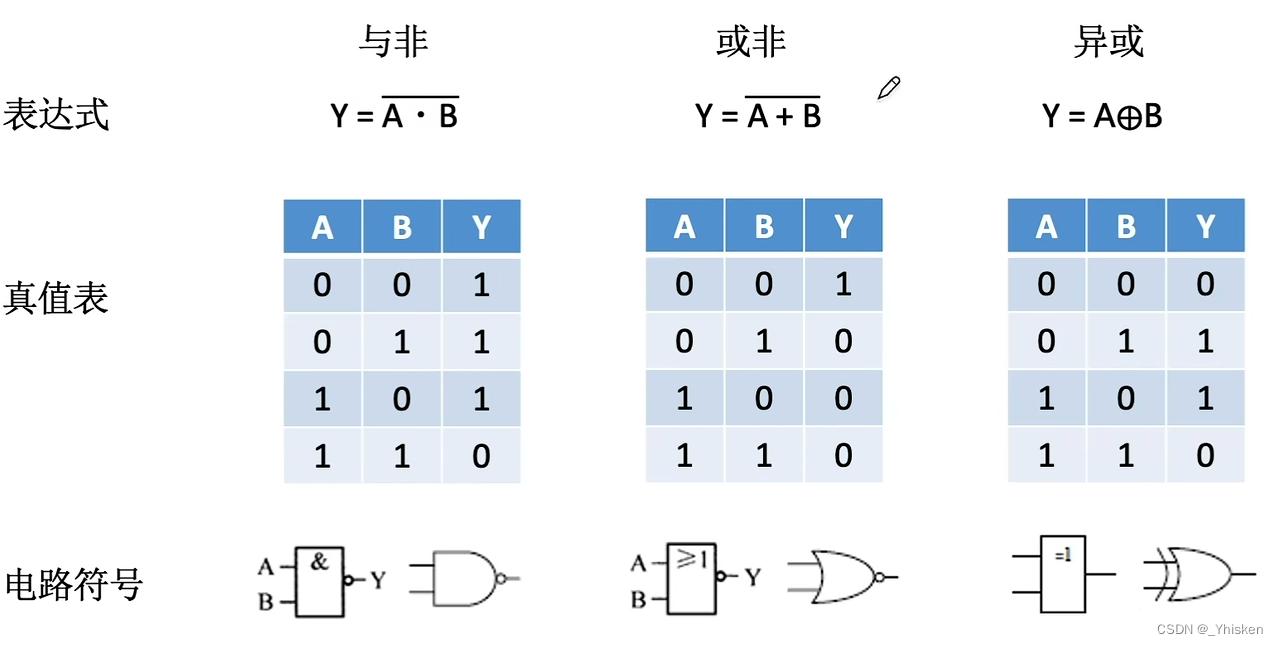
与非就是先进行与运算，再进行非运算。

或非就是先进行或运算，再进行非运算。

异或运算则是 相同为0，不同为1。 三种符合逻辑的电路构成如上图所示。

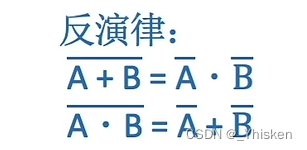
同时，有反演律，让我们可以把或非转换成非的与，把与非转换成非的或。 

(1)异或门的逻辑实现

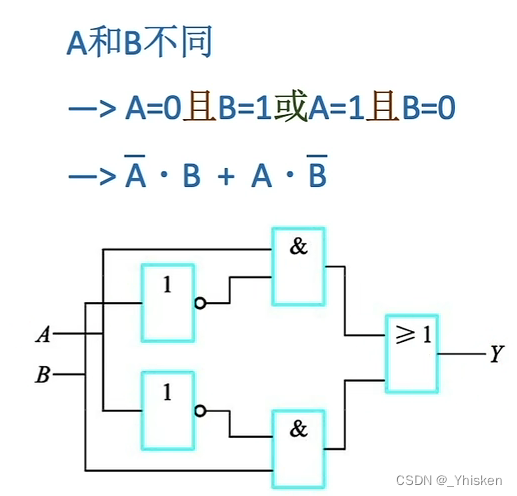
异或操作我们说是一种符合逻辑运算，因此我们可以用基本的逻辑运算实现，如上图所示。

分析得知A，B不同情况，A=0且B=1或A=1且B=0，即可得出逻辑表达式从而设计电路。

(2)同或运算

同或运算其实就是异或运算的取反

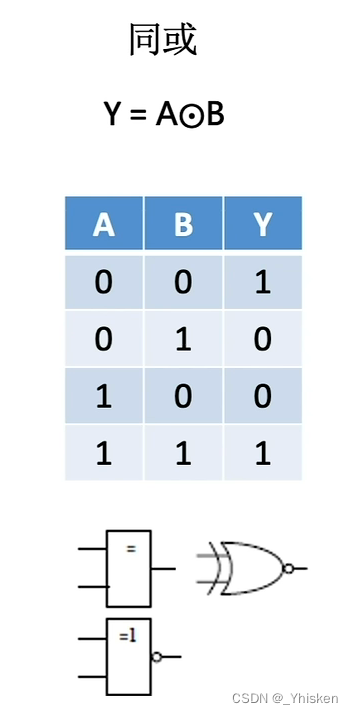
(3)异或门实现奇偶校验

通过以上的基本逻辑运算和符合逻辑运算，我们可以组成更复杂的逻辑运算，比如奇偶校验。奇偶校验和我们的异或门逻辑是对应的，所以完全可以由异或门实现。同时异或门也是天然的加法运算。

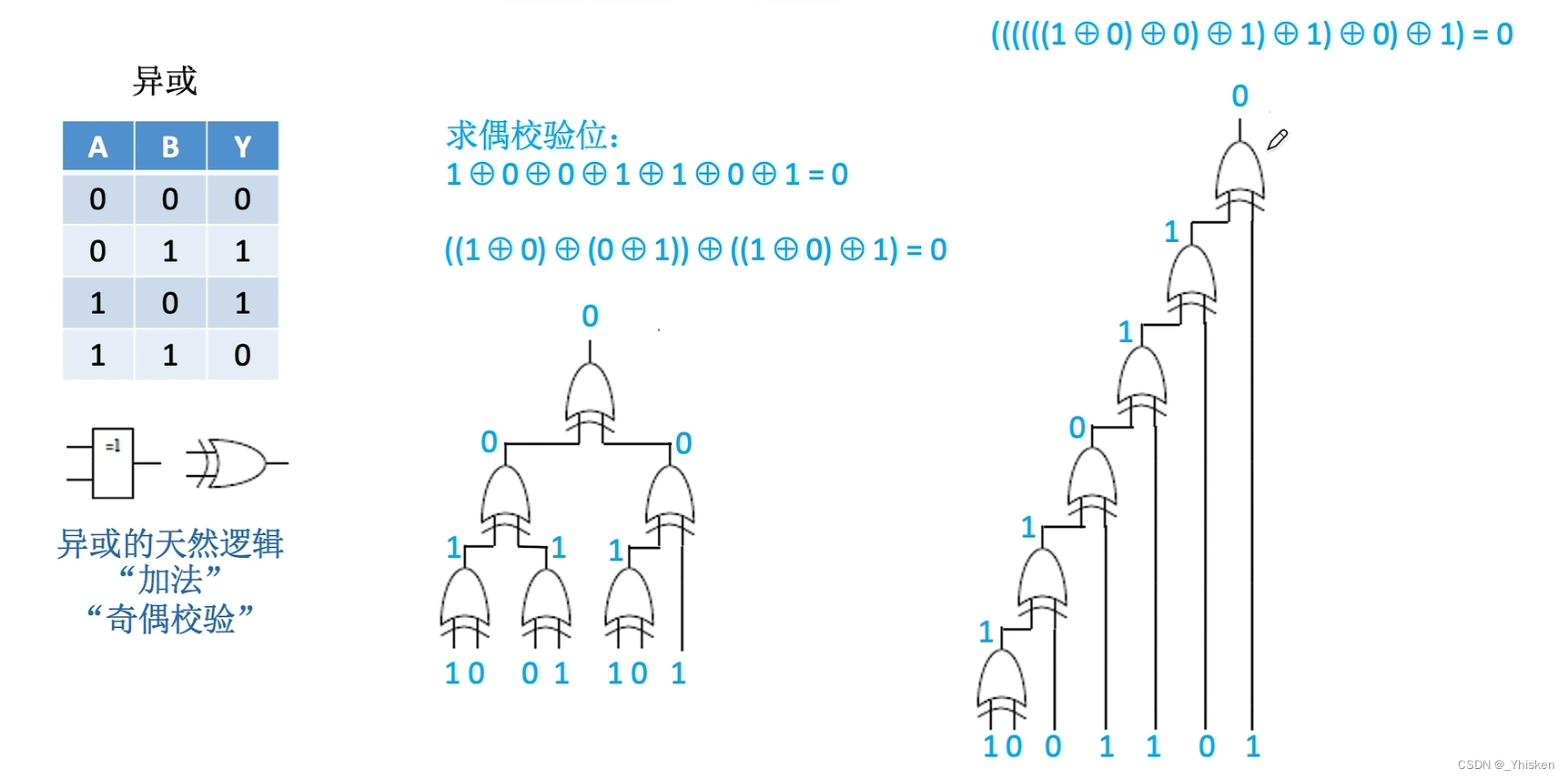
如上图所示，是两种不同计算顺序的逻辑表达式实现求偶校验位对应的异或门电路。（本质上就是判断有奇数个1还是偶数个1）

(4)异或门实现加法运算

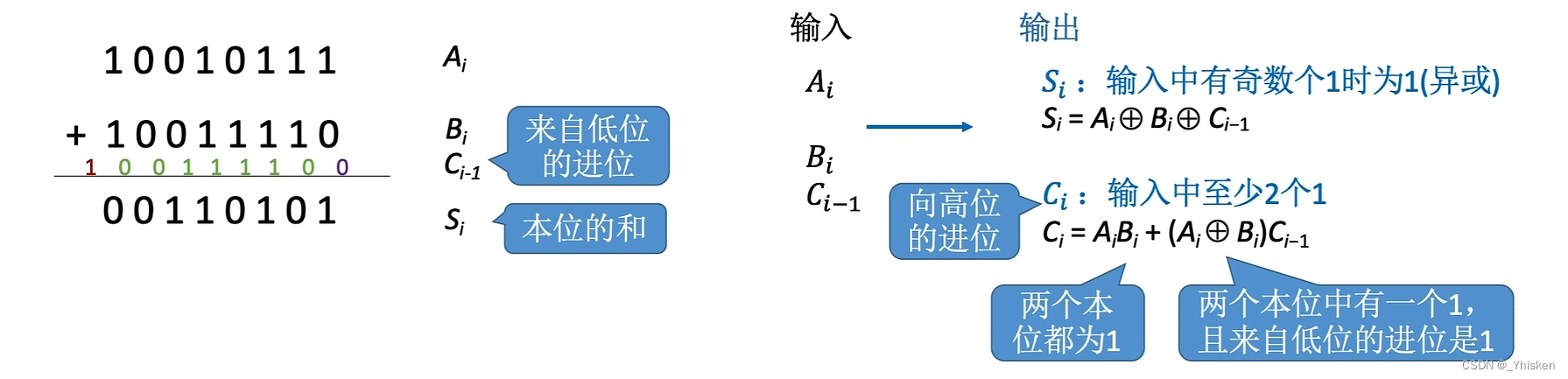
我们知道加法会产生进位，如上图8bit的加法所示。那么本位的和Si和是否进位由三个数决定，被加数的本位Ai，加数的本位Bi，以及来自低位的进位Ci-1。

很容易知道，Si由Ai和Bi的异或结果与Ci-1的异或得到，如上图所示。

而是否产生进位，则有两种情况，首先至少有2个1才能产生进位。那么2个1的情况有两种，我们需要进行或运算，一种情况是两个本位Ai和Bi都为1，或者Ai，Bi其中一个为1，然后进位是1。

一位全加器

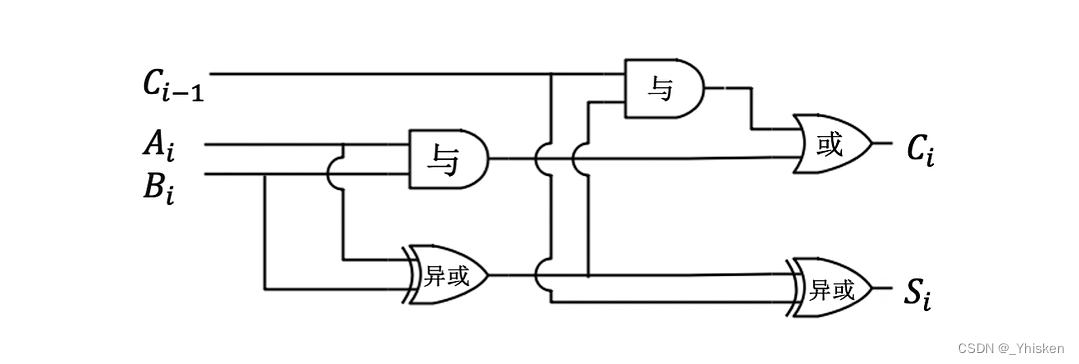
根据上面推断出的不同情况，列出逻辑表达式之后，我们就可以很容易的得到一位全加器（FA，Full Adder）的门电路表示，如上图所示。

(5)多位加法的实现——串行加法器

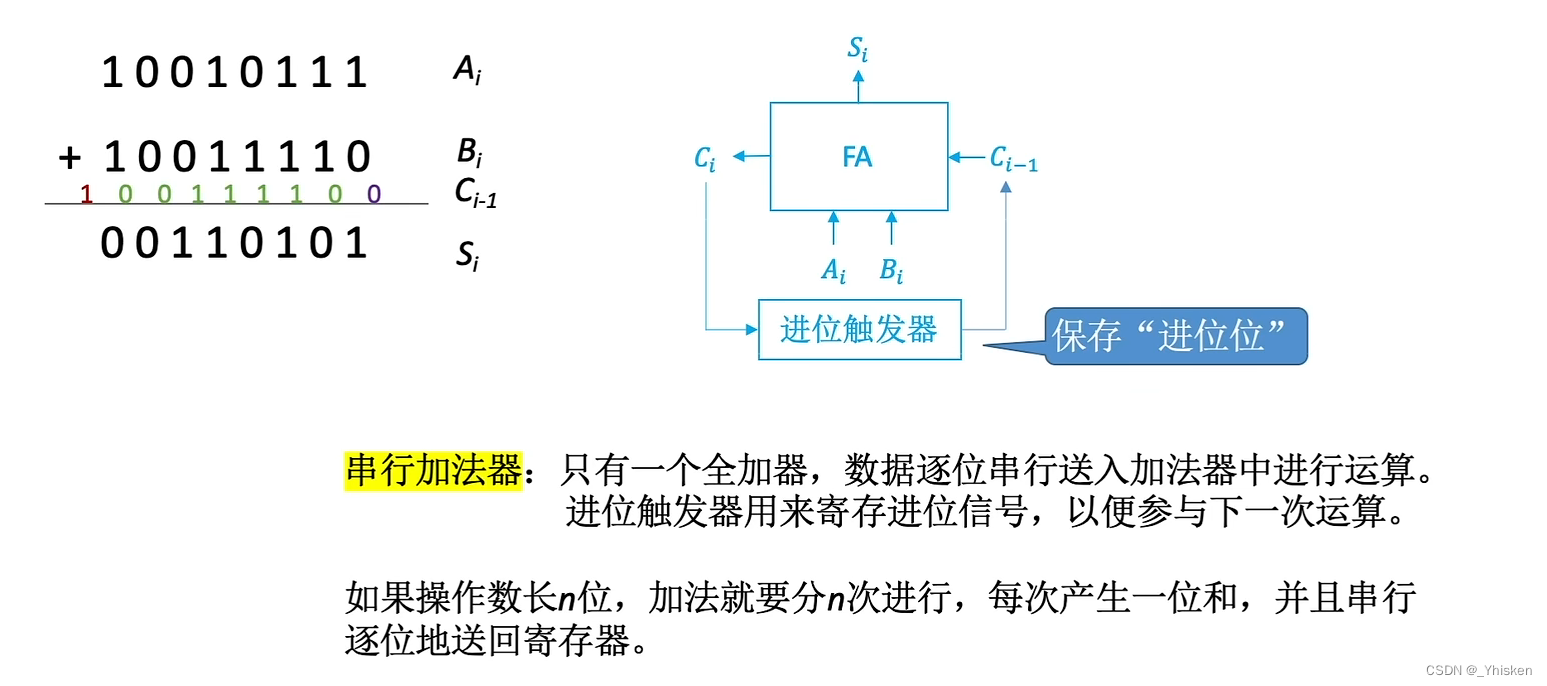
串行加法器，顾名思义就是串行运算。它是通过一位一位的运算来实现加法的，也正是因为如此，它只有一个一位全加器和一个进位触发器构成。 一位全加器负责我们上面提到的本位运算，而进位触发器则负责保存进位位。因为本位的进位位会决定高位的进位位。

以上图为例，最开始的Ai=1，Bi=0，Ci-1=0，经过一位全加器后得到高位进位位Ci为0，

接着进行高位运算Ai=1，Bi=1，Ci-1=0，经过一位全加器后得到高位进位位Ci为1。

继续进行高位运算Ai=1，Bi=1，Ci-1=1，经过一位全加器后得到高位进位位Ci为1。

以此类推……可以看到，由于逐位的运算，如果操作数长n位，就需要进行n次加法，并且需要串行送回寄存器，所以串行加法器的效率是比较低的。

---

(6)串行进位的并行加法器

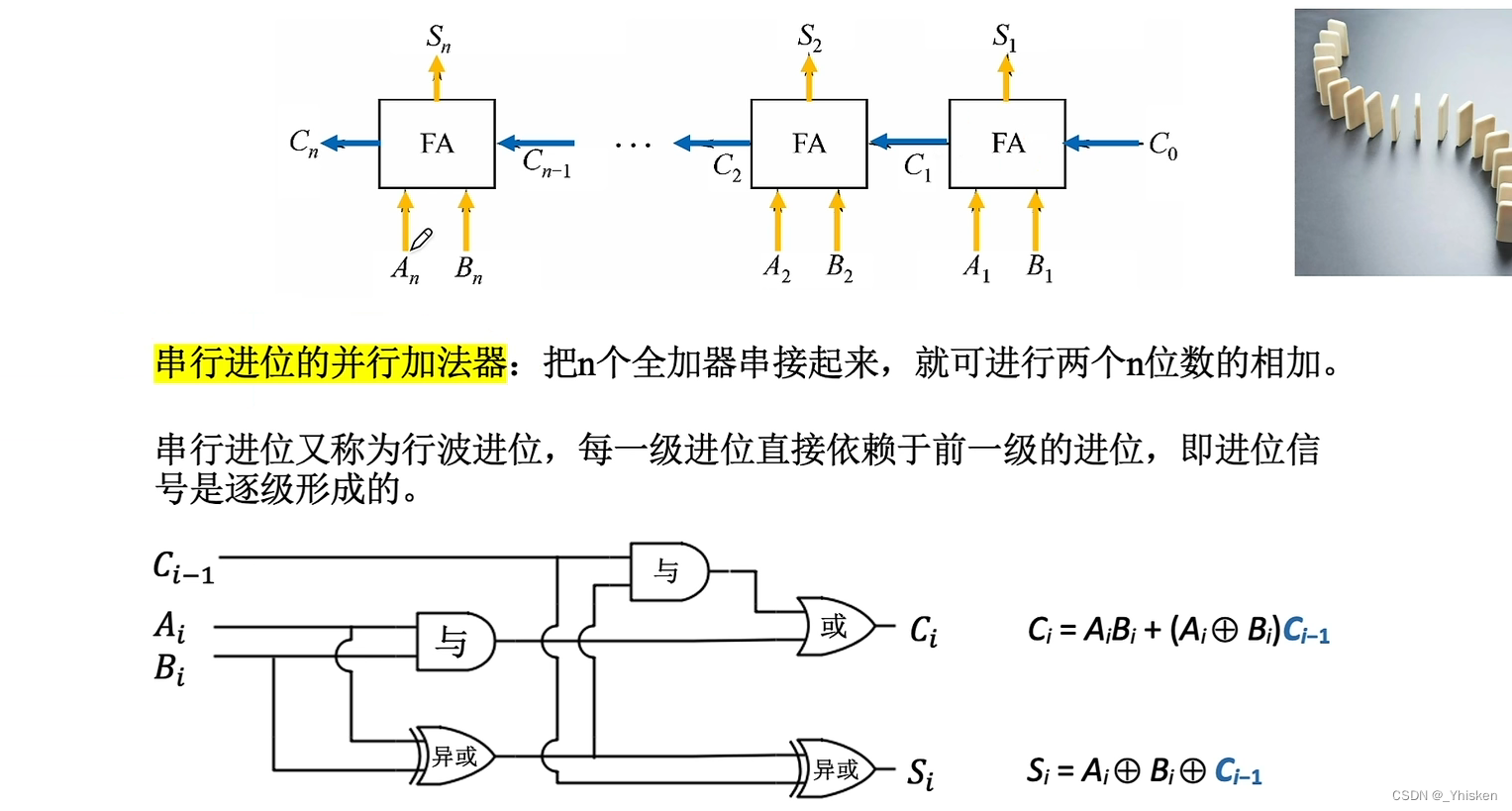
我们可以把多个一位全加器串联起来，组成串行进位的并行加法器，这样就可以同时输入n位的数，同时低位的进位会作为高位全加器的一个输入信号。

虽然我们可以同时输入A，B数值位的信息，但是电信号的传递依然是串行。也就是说只有低位运算结束之后，才知道往高位进的信号是什么，而高位的进位信号可能会导致更高位的进位信号发生改变，所以我们称之为串行进位的并行加法器。

以此，串行进位的并行加法器的进位信号是逐级形成的，只有来自低位的进位信号决定了，我们才能决定本位和和更高位的进位信号。因此串行进位的并行加法器的运算速度很大程度上取决于我们每一位进位的产生速度。