CCF CSP认证 历年题目自练Day31
题目一
试题编号: 202206-1
试题名称: 归一化处理
时间限制: 500ms
内存限制: 512.0MB
题目背景
在机器学习中,对数据进行归一化处理是一种常用的技术。
将数据从各种各样分布调整为平均值为 0、方差为 1的标准分布,在很多情况下都可以有效地加速模型的训练。

样例输入
7
-4 293 0 -22 12 654 1000
Data
样例输出
-0.7485510379073613
0.04504284674812264
-0.7378629047806881
-0.7966476369773906
-0.7057985054006686
1.0096468614303775
1.9341703768876082

题目分析(个人理解)
- 此题送分题,还是先看输入,第一行输入n,第二行输入n个数,每个数用空格分开。
- 再看输出,求的是每个数减去平均数在除以方差。
- 还是选择列表存储我将所有值都存入列表。我采用列表推导式。
l=[i for i in map(int,input().split())] - 然后用sum函数求和除以n获得平均数,用math库的sqrt函数来开根号求得F(ai)。
- 最后遍历输出fa即可。
- 上代码!!!
import math
D=[]
mean=0
n=int(input())
l=[i for i in map(int,input().split())]
mean=sum(l)/n
for i in range(n):d=abs(l[i]-mean)**2#不用abs求绝对值也行,只是数学逻辑严谨一些D.append(d)
Da=math.sqrt(sum(D)/n)
for i in range(n):fa=(l[i]-mean)/Daprint(fa)
题目二
试题编号: 202206-2
试题名称: 寻宝!大冒险!
时间限制: 500ms
内存限制: 512.0MB
题目背景
暑假要到了。可惜由于种种原因,小 P 原本的出游计划取消。失望的小 P 只能留在西西艾弗岛上度过一个略显单调的假期……直到……某天,小 P 获得了一张神秘的藏宝图。

输出格式
输出到标准输出。
输出一个整数,表示绿化图中有多少处坐标可以与藏宝图左下角对应,即可能埋藏着顿顿的宝藏。
样例 1 输入
5 100 2
0 0
1 1
2 2
3 3
4 4
0 0 1
0 1 0
1 0 0
Data
样例 1 输出
3
Data
样例 1 解释
绿化图上 (0,0)(1,1)(2,2)三处均可能埋有宝藏。
样例 2 输入
5 4 2
0 0
1 1
2 2
3 3
4 4
0 0 0
0 1 0
1 0 0
Data
样例 2 输出
0
Data
样例 2 解释
如果将藏宝图左下角与绿化图 (3,3) 处对应,则藏宝图右上角会超出绿化图边界,对应不成功。
题目分析(个人理解)
- 还是先读题目,大意是这样的,有一张地图A(绿化图,题目是这么叫的),用类矩阵表示里面只有数值1或0,1代表有树,0代表没树。还有一张图B(也就是题目中的藏宝图),B图比A图小,一样只有1或0表示是否有树,如何判断宝藏地点?
- 绿化图中有多少处坐标可以与藏宝图左下角对应,即可能埋藏着顿顿的宝藏。如何理解?就是满足b图作为A图的子图(0和1位置完全符合)且B图的左下角(只有一个点)才是一个藏宝地点,那么我只需要按照B图的大小以及数值,遍历A图(0和1)判断满足有几个子图那么就说明有几个藏宝地点。这里尤其注意输入,不管A图还是B图都是左下角是(0,0)点,而且,最先输入的是B[s][0]最后输入的是B[0][s];所以当给B图赋值的时候要倒序遍历。
- 那么如何判断满不满足B图是A图的子图的条件呢?只需要从a图左下角依次遍历以b图左下角为开始到右上角的值是否都相等,如果都相等,那么就是子图,否则则不是。
- 代码如何具体实现?我选择列表存储A图和B图,具体用列表推导式,用二维列表表示01矩阵。
- 然后分别将A,B两图的值输入,然后依次(从A图左下角开始)把和B图同等大小的A图的局部图抠下来,去和B图判断是否相等即可。如果相等计数器加1,最后输出计数器数值。
- 上代码!!!(只能拿70分,因为抠下来的图太多了,占用空间太大)
n, L, S = map(int, input().split()) # n棵树,L绿化图大小,S藏宝图大小
A = [[0 for _ in range(L+1)] for _ in range(L+1)] # A绿化图坐标
t = [] # 树的坐标列表
for _ in range(n): # 把n棵树写到A绿化图中x, y = map(int, input().split()) # 每棵树的坐标t.append([x,y])A[x][y] = 1
B = [[0 for _ in range(S+1)] for _ in range(S+1)] # B藏宝图坐标
for i in range(S,0-1,-1): # 把局部树写到B藏宝图中B[i] = list(map(int, input().split()))res = 0 # 可能情况的数量
for i in t:if i[0] + S <= L and i[1] + S <= L:T = [] # 同大小局部绿化图坐标for j in range(S+1):T.append(A[i[0]+j][i[1]:i[1]+S+1])if T == B:res = res + 1
print(res)- 只能换个思路了,第二种方法是这样的:
- 我完全可以只遍历A图中有树(值为1)的位置,作为B图的左下角(B图左下角必须有树,题目告诉了藏宝图左下角一定是一棵树)。那么我只需要遍历n次就可以判断完全。
- 为了减少判断次数,可先将是否满足B图是A图的子图作为第一个判断条件,具体就是如果A图中值为1坐标x,y轴分别加上B图的横,纵长度如果超过A图的大小就不满足是A图子图的条件,那么就没必要进行下一步判断了。
10.上代码!!!
# 输入三个正整数 n、L 和 S,分别表示西西艾弗岛上树的棵数、绿化图和藏宝图的大小
n, l, s = map(int, input().split())
# 输入每棵树的坐标
points = [[i for i in map(int,input().split())] for j in range(n)]
# 将树的坐标整理成集合的形式,方便后面进行地图与树位置的比对
temp = {}
for point in points:x, y = point[0], point[1]temp[(x, y)] = 1
# 建立藏宝图
money = []
for i in range(s+1):money.insert(0, list(map(int, input().split())))
# 设置time值来记录绿化图中有多少处坐标可以与藏宝图左下角对应
time = 0
# 开始遍历树的坐标与藏宝图中的树的坐标进行比对
for x, y in points:# 设置一个标志值来判定是否符合藏宝图要求flag = 0# 开始遍历比对for i in range(s+1):for j in range(s+1):if (x+i > l) or (y+j > l): #藏宝图的要求:大小必然小于绿化图flag = 1breakif money[i][j]: if (x+i, y+j) not in temp:flag = 1breakelse: if (x+i, y+j) in temp:flag = 1breakif flag == 1: breakif flag == 0:time += 1
print(time)总结

相关文章:

CCF CSP认证 历年题目自练Day31
题目一 试题编号: 202206-1 试题名称: 归一化处理 时间限制: 500ms 内存限制: 512.0MB 题目背景 在机器学习中,对数据进行归一化处理是一种常用的技术。 将数据从各种各样分布调整为平均值为 0、方差为 1的标准分布&a…...
)
PCL点云处理之从两片点云中获取具有匹配关系的同名点对 (二百一十八)
PCL点云处理之从两片点云中获取具有匹配关系的同名点对 (二百一十八) 一、算法介绍二、算法实现1.代码2.效果一、算法介绍 点云配准的前提是,我们知道或者预测了一些匹配对,我们认为这些匹配对就是两片点云中的同名点,同名点就是由于激光扫描存在误差的关系,导致同一地物…...
MySQL Row size too large (> 8126)
错误信息 ERROR 1118 (42000) at line 901: Row size too large (> 8126). Changing some columns to TEXT or BLOB or using ROW_FORMATDYNAMIC or ROW_FORMATCOMPRESSED may help. In current row format, BLOB prefix of 768 bytes is stored inline. 错误原因 这个问题…...
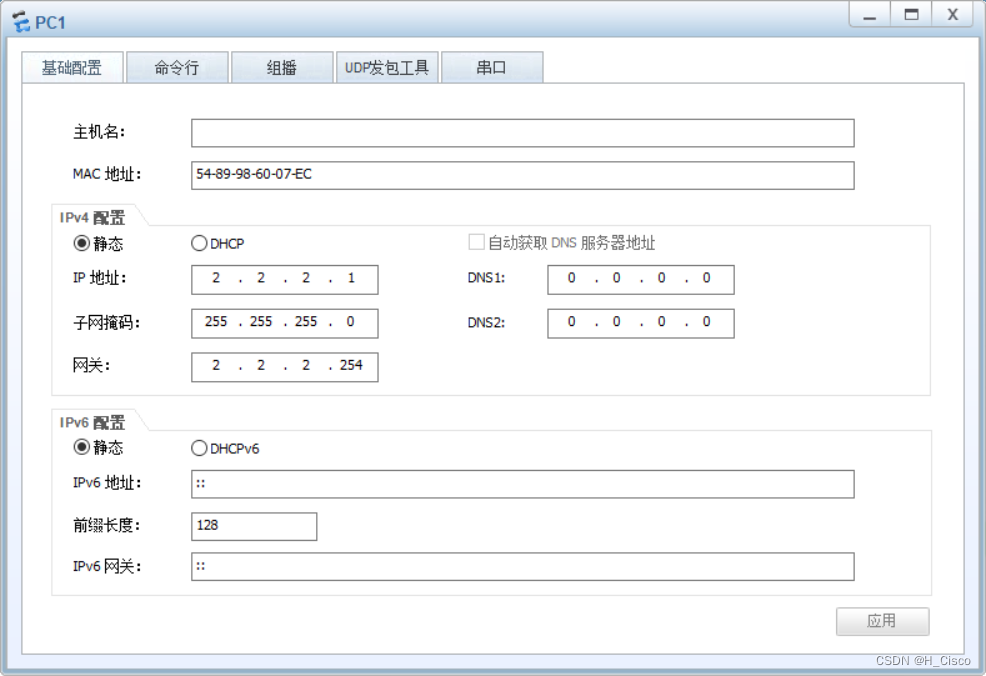
HUAWEI(26)——防火墙双机热备
一、拓扑 二、需求 PC2 ping PC1 FW1与FW2双机热备,FW1为active,FW2为Standby,抢占延时1s VRRP 三、配置 1.IP地址,防火墙接口加入区域 防火墙用户名:admin 防火墙旧密码:Admin@123 防火墙新密码:admin@123 [FW1]interface GigabitEthernet 1/0/0 [FW1-GigabitEthe…...

【ArcGIS】NDVI估算植被覆盖度FVC
NDVI估算植被覆盖度FVC NDVI计算植被覆盖度FVC计算NDVI估算植被覆盖度FVC操作步骤Step1:调出栅格计算器工具Step2:查找NDVIStep3: 参考 NDVI计算 植被覆盖度FVC计算 NDVI估算植被覆盖度FVC操作步骤 Step1:调出栅格计算器工具 1、首先打开软件&#x…...

vscode用密钥文件连接ssh:如果一直要输密码怎么办
commandshiftP:打开ssh配置文件 加上这么一段,host就是你给主机起的名字 对IdentityFile进行更改,改成相应的密钥文件 然后commandshiftP链接到主机就可以了 但是有时候它会让输入密码 这是由于你给这个IdentityFile的权限太多了…...

【AI视野·今日Robot 机器人论文速览 第五十三期】Thu, 12 Oct 2023
AI视野今日CS.Robotics 机器人学论文速览 Thu, 12 Oct 2023 Totally 25 papers 👉上期速览✈更多精彩请移步主页 Daily Robotics Papers Pixel State Value Network for Combined Prediction and Planning in Interactive Environments Authors Sascha Rosbach, St…...

【LeetCode第115场双周赛】100029. 和带限制的子多重集合的数目 | 前缀和背包 | 中等
题目内容 原题链接 给定一个长度为 n n n 的数组 n u m s nums nums 和一个区间左右端点 [ l , r ] [l,r] [l,r] 。 返回 n u m s nums nums 中子多重集合的和在闭区间 [ l , r ] [l, r] [l,r] 之间的 子多重集合的数目 。 子多重集合 指的是从数组中选出一些元素构成的 …...

ArcGIS笔记5_生成栅格文件时保存报错怎么办
本文目录 前言Step 1 直接保存到指定文件夹会报错Step 2 先保存到默认位置再数据导出到指定文件夹 前言 有时生成栅格文件时,保存在自定义指定的文件夹内会提示出错,而保存到默认位置则没有问题。因此可以通过先保存到默认位置,再数据导出到…...

YOLO目标检测——跌倒摔倒数据集【含对应voc、coco和yolo三种格式标签】
实际项目应用:公共安全监控、智能家居、工业安全等活动区域无监管情况下的人员摔倒事故数据集说明:YOLO目标检测数据集,真实场景的高质量图片数据,数据场景丰富。使用lableimg标注软件标注,标注框质量高,含…...
uniapp小程序实现绘制内容,生成海报并保存截图(Painter和Canvas两种方式举例)
一、Painter方法 Painter插件传送门 1.下载资源包 2.将资源包的如下部分 3.使用页面引入组件 ui样式 <paintercustomStyle=margin-left: 40rpx; height: 1000rpx;palette="{{palette}}"bind:imgOK="onImgOK"/>data 中数据(绘制内容,替换区域) pai…...

HTTPS双向认证及密钥总结
公钥私钥: 1)公钥加密,私钥解密:加解密 为什么不能私钥加密公钥解密? 私钥加密后,公钥是公开的都能解密,没有意义。 2)私钥签名,公钥验签:属于身份验证,防串改&#x…...
Mybatis用Byte[]存图片,前端显示图片
前端页面 static下 也就是说byte[] 转成JSON字符串后,和用BASE64编码后是一摸一样的,那么SpringBoot会自动将实体类转JSON字符串,也就是说根本不需要Base64编码 注意:两个值并非一摸一样,一个多了个双引号 byte[]的值前后有个双引号 有一点点区别 一个有双引号,一个没有…...

MacBook/MacOS如何更新到指定的版本
背景 现在是A版本,想要更新到B,而目前能最新更新到C。 是可以做到的,不一定更新就得更新到最新的。 只要下载好B之后更新即可。 方法 思路是下载好目标的版本后更新,这里可以下载: https://support.apple.com/zh-…...

使用VScode进行C++开发
需要的两个文件 .vscode 目录下 tasks.json {"tasks": [{"type": "cppbuild","label": "C/C: g.exe 生成活动文件","command": "C:/MinGW/bin/g.exe","args": ["-fdiagnostics-color…...

Android Studio的笔记--HttpsURLConnection使用POST请求
HttpsURLConnection使用POST请求 https post请求加返回MainActivity.javaAndroidMainfest.xmlactivity_main.xmllog https post请求加返回 MainActivity.java 用HttpsURLConnection POST方法进行需注意: 1、Android 9及以上版本需要设置这个,否则会有警…...

win redis 配置自启动服务
配置自启动 redis-server --service-install redis.windows-service.conf --loglevel verbose redis.windows-service.conf 配置 Logs 文件夹...

走进Spark
什么是Spark 是一个基于内存的,用于大规模数据处理(离线计算、实时计算、快速查询(交互式查询))的统一分析引擎,因为是基于内存的所以可以更快的完成任务 离线计算:离线计算一般存储在HDFS中使用MapReduce或…...
“小程序:改变电商行业的新趋势“
目录 引言1. 小程序的简介1.1 什么是小程序?1.2 小程序的优势 2. 小程序之电商演示1.注册微信小程序2.安装开发工具3.创建项目 3. 小程序之入门案例总结 引言 随着移动互联网的迅猛发展,小程序作为一种全新的应用形态,正在逐渐改变着传统电商…...
创建图案填充)
Python与CAD系列基础篇(五)创建图案填充
目录 0 简述1 win32com2 ezdxf0 简述 本篇详细介绍使用①pyautocadpyautocad本质是调用接口连接autocad,由于此处未找到正确的填充函数,通过win32com库找到相应填充函数,测试发现更为好用,因此后续将用win32com代替pyautocad连接AutoCAD进行处理 ②通过ezdxf处理dxf格式文…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

HTML 列表、表格、表单
1 列表标签 作用:布局内容排列整齐的区域 列表分类:无序列表、有序列表、定义列表。 例如: 1.1 无序列表 标签:ul 嵌套 li,ul是无序列表,li是列表条目。 注意事项: ul 标签里面只能包裹 li…...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...
)
安卓基础(aar)
重新设置java21的环境,临时设置 $env:JAVA_HOME "D:\Android Studio\jbr" 查看当前环境变量 JAVA_HOME 的值 echo $env:JAVA_HOME 构建ARR文件 ./gradlew :private-lib:assembleRelease 目录是这样的: MyApp/ ├── app/ …...

视频行为标注工具BehaviLabel(源码+使用介绍+Windows.Exe版本)
前言: 最近在做行为检测相关的模型,用的是时空图卷积网络(STGCN),但原有kinetic-400数据集数据质量较低,需要进行细粒度的标注,同时粗略搜了下已有开源工具基本都集中于图像分割这块,…...

Java数值运算常见陷阱与规避方法
整数除法中的舍入问题 问题现象 当开发者预期进行浮点除法却误用整数除法时,会出现小数部分被截断的情况。典型错误模式如下: void process(int value) {double half = value / 2; // 整数除法导致截断// 使用half变量 }此时...
