大厂真题:【模拟】OPPO2023秋招提前批-小欧数组求和
题目描述与示例
题目描述
小欧拿到了一个数组,她有q次操作,每次操作修改一个元素。小欧希望每次修改后得到当前数组所有元素之和。你能帮帮她吗?
输入描述
第一行输入两个正整数n和q,代表数组的大小和操作次数。
第二行输入n个正整数ai,代表小欧拿到的初始数组。
接下来的q行,每行输入两个正整数i和x,代表将第i个元素修改为x。
输出描述
输出q行,每行输出一个正整数,代表当前数组元素之和。
示例
输入
5 3
1 2 3 4 5
2 3
3 3
5 1
输出
16
16
12
说明
第一次修改后,数组变成[1,3,3,4,5],元素之和为16。
第二次修改后,数组变成[1,3,3,4,5],元素之和为16。
第三次修改后,数组变成[1,3,3,4,1],元素之和为12。
解题思路
本题属于非常简单的模拟题。
对于某一次特定的修改,假设我们已知上一次修改后的数组和为nums_sum,而本次修改将nums[i]修改为x,那么修改后的和应该为nums_sum-nums[i]+x。而此处修改后的和又可以作为下一次修改的上一次修改后的数组和来使用,即存在
nums_sum = nums_sum - nums[i] + x
需要被在本次修改后输出。同时nums[i]需要修改为x。上述核心代码为
nums_sum -= nums[i]
nums_sum += x
nums[i] = x
本题要特别注意,题目最后q行输入的索引值是从1开始的,故映射到数组的索引值,必须进行i -= 1的修改。
代码
Python
# 题目:【模拟】OPPO2023秋招提前批-小欧数组求和
# 作者:闭着眼睛学数理化
# 算法:模拟
# 代码有看不懂的地方请直接在群上提问# 数组长度n,操作次数q
n, q = map(int, input().split())
# 初始数组nums
nums = list(map(int, input().split()))
# 计算初始数组nums的和
nums_sum = sum(nums)
# 储存q次修改的结果
ans = list()# 循环q次,修改q次
for _ in range(q):# 修改的位置i和修改的内容xi, x = map(int, input().split())# 注意i输入表示的是第i个元素,将其改为索引需要-1i -= 1# 将nums[i]修改为x,则整体的和需要减少nums[i],增加xnums_sum -= nums[i]nums_sum += x# 同时nums[i]被修改为xnums[i] = x# 将本次修改后的数组和nums_sum储存在ans中,方便后续按顺序输出ans.append(nums_sum)for num in ans:print(num)
Java
import java.util.Scanner;public class Main {public static void main(String[] args) {Scanner scanner = new Scanner(System.in);int n = scanner.nextInt();int q = scanner.nextInt();int[] nums = new int[n];for (int i = 0; i < n; i++) {nums[i] = scanner.nextInt();}int numsSum = 0;for (int num : nums) {numsSum += num;}int[] ans = new int[q];for (int k = 0; k < q; k++) {int i = scanner.nextInt() - 1;int x = scanner.nextInt();numsSum -= nums[i];numsSum += x;nums[i] = x;ans[k] = numsSum;}for (int num : ans) {System.out.println(num);}}
}
C++
#include <iostream>
using namespace std;int main() {int n, q;cin >> n >> q;int nums[n];for (int i = 0; i < n; i++) {cin >> nums[i];}int numsSum = 0;for (int i = 0; i < n; i++) {numsSum += nums[i];}int ans[q];for (int k = 0; k < q; k++) {int i, x;cin >> i >> x;i--;numsSum -= nums[i];numsSum += x;nums[i] = x;ans[k] = numsSum;}for (int i = 0; i < q; i++) {cout << ans[i] << endl;}return 0;
}
时空复杂度
时间复杂度:O(N+q)。第一次计算nums的和的时间复杂度为O(N),进行q次修改的时间复杂度为O(q)
空间复杂度:O(1)。仅需若干常数变量。
华为OD算法/大厂面试高频题算法练习冲刺训练
-
华为OD算法/大厂面试高频题算法冲刺训练目前开始常态化报名!目前已服务100+同学成功上岸!
-
课程讲师为全网50w+粉丝编程博主@吴师兄学算法 以及小红书头部编程博主@闭着眼睛学数理化
-
每期人数维持在20人内,保证能够最大限度地满足到每一个同学的需求,达到和1v1同样的学习效果!
-
60+天陪伴式学习,40+直播课时,300+动画图解视频,300+LeetCode经典题,200+华为OD真题/大厂真题,还有简历修改、模拟面试、专属HR对接将为你解锁
-
可上全网独家的欧弟OJ系统练习华子OD、大厂真题
-
可查看链接 OD算法冲刺训练课程表 & OD真题汇总(持续更新)
-
绿色聊天软件戳
od1336了解更多
相关文章:

大厂真题:【模拟】OPPO2023秋招提前批-小欧数组求和
题目描述与示例 题目描述 小欧拿到了一个数组,她有q次操作,每次操作修改一个元素。小欧希望每次修改后得到当前数组所有元素之和。你能帮帮她吗? 输入描述 第一行输入两个正整数n和q,代表数组的大小和操作次数。 第二行输入n…...

Python括号匹配问题
给定一个只包含小写字母的字符串,判断该字符串中的括号是否闭合,如果每个左括号都有对应的右括号,并且括号的嵌套顺序正确,那么括号就能正确闭合。 否则,括号不能正确闭合,字符串中括号仅限于 "("…...
微信小程序备案内容常见问题汇总
一、备案时间点 自2023年09月01日起,新的微信小程序,必须备案后才能上架; 在2024年03月31日前,所有小程序都必须完成备案; 于2024年04月01日起,对未备案小程序进行清退处理。 微信小程序备案系统已于9月4日上线。 二、备案流程 [找备案入口]–[填主体信息]–[填小程…...

无人机新手防炸飞行技巧
不要在室内飞行,容易撞墙。起飞前设置好避障和返航模式。使用模拟器熟练掌握操控。选择开阔环境目视起飞。使用低速档平稳飞行。合理使用避障功能,不要盲目依赖。使用九宫格避障法。留意电量,及时返航。极低电量时放弃强行返航。飞行后及时为电池充电保养。...

webrtc opus 音频编码支持SILK和CELT模式
SILK CELT是指将SILK编解码器和CELT编解码器结合在一起的混合音频编码方案。 SILK(Super-wideband audio coding)是一种低延迟的音频编解码器,用于实时的语音通信。它提供高质量的音频传输,并且适用于各种比特率和带宽条件。SILK…...

掌握Python爬虫实现网站关键词扩展提升曝光率
目录 一、关键词优化的重要性 二、关键词优化的基本方法 1、选择与网站内容相关的关键词 2、控制关键词的密度和分布 3、关键词的层次布局 三、Python爬虫实现网站关键词扩展 1、确定目标网站 2、分析目标网站的HTML结构 3、编写Python爬虫代码 4、分析爬取到的关键词…...

ajax实现原理
网页应用能够快速地将增量更新呈现在用户界面上,而不需要重载(刷新)整个页面。这使得程序能够更快地回应用户的操作 Ajax的实现原理 创建Ajax对象 传入请求方式和请求地址 发送请求 获取服务器与客户端的响应数据 xhr.responseText // 1…...

图G的拉普拉斯矩阵为什么由L=D-A定义
图G的拉普拉斯矩阵由LD-A定义,其中D是度矩阵(Degree Matrix),A是邻接矩阵(Adjacency Matrix)。这种定义方式有以下原因: 1. 度矩阵D:度矩阵是一个对角矩阵,其对角线上的…...

实习项目遇到的bug
问题1: 大概是因为没设置ts类型,它查不到的问题,不定义的话加上问号,加上可选链就不会报错了 {{bizEquipmentInfo.lastUnlockingVO?.lastUnlockingTime.replace(T, )? bizEquipmentInfo.lastUnlockingVO?.lastUnlockingTime.r…...
)
python selenium下载一个合适的chromedriver.exe(稳定版本)
可以使用该脚本来进行下载: 下载前需要安装如下的依赖 requests2.27.1 selenium4.14.0 webdriver_manager4.0.1下载脚本代码: import json import subprocess import shutil import os import time import zipfileimport requests from webdriver_mana…...
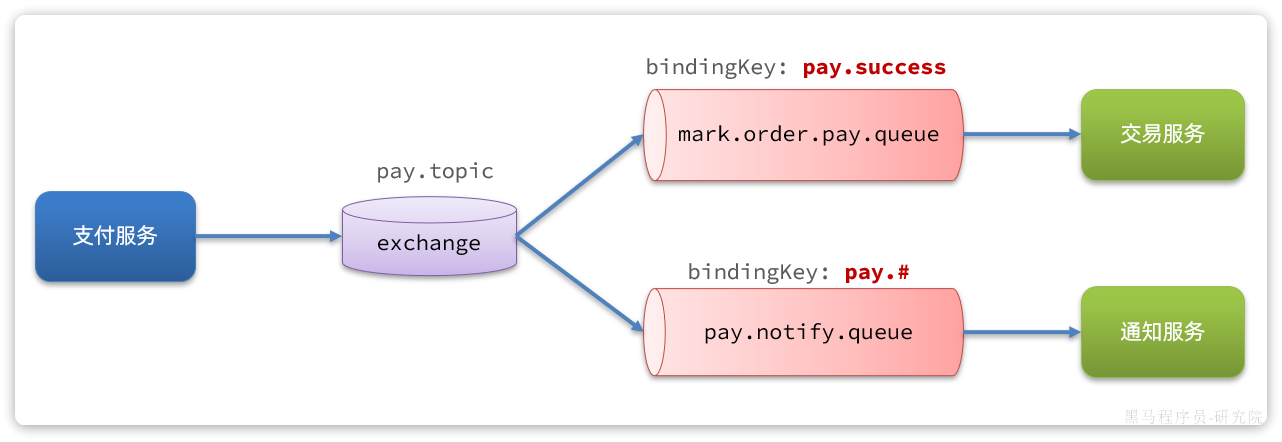
RabbitMQ从0到1完整学习笔记一:《基础篇》
目录 启篇 一、初识MQ 1.1 同步调用 1.2异步调用 1.3 技术选型 二、RabbitMQ 架构 2.2 收发消息 2.2.1 交换机 2.2.2 队列 2.2.3 绑定关系 2.2.4 发送消息 2.3 数据隔离 2.3.1 用户管理 2.3.2 virtual host 三、SpringAMQP 3.1 案例入门 3.1.1 导入依赖 3.1.2 消息发送 3.1.2 消…...

什么是时间冒泡?
时间冒泡是指当一个元素触发一个事件时,事件会像水泡一样,从触发元素向它的所有父节点传播,一直到根节点都会接收到此事件 1。如果父元素中注册了相应的事件处理函数,那么尽管事件在子节点触发的,在父元素上注册的事件…...

Go语言入门心法(三): 接口
Go语言入门心法(一) Go语言入门心法(二): 结构体 Go语言入门心法(三): 接口 一:go语言接口认知 Go语言中接口认知升维:解决人生问题的自我引导法则: 复盘思维|结构化思维|金字塔思维|体系化思维|系统化思维 面向对象编程(oop)三大特性: 封装,继承,多态 Go语言中,可…...

leetcode:210. 课程表 II
课程表 II 提示 中等 889 相关企业 现在你总共有 numCourses 门课需要选,记为 0 到 numCourses - 1。给你一个数组 prerequisites ,其中 prerequisites[i] [ai, bi] ,表示在选修课程 ai 前 必须 先选修 bi 。 例如,想要学习课程…...

[MT8766][Android12] 使用谷歌LPA实现ESIM功能的流程
文章目录 开发平台基本信息问题描述实现流程 其他问题 开发平台基本信息 芯片: MT8766 版本: Android 12 kernel: msm-4.19 问题描述 客户需要我们设备支持ESIM功能,5月份的时候在高通6125上面预研过ESIM功能,当时ESIM供应商是Links field,…...
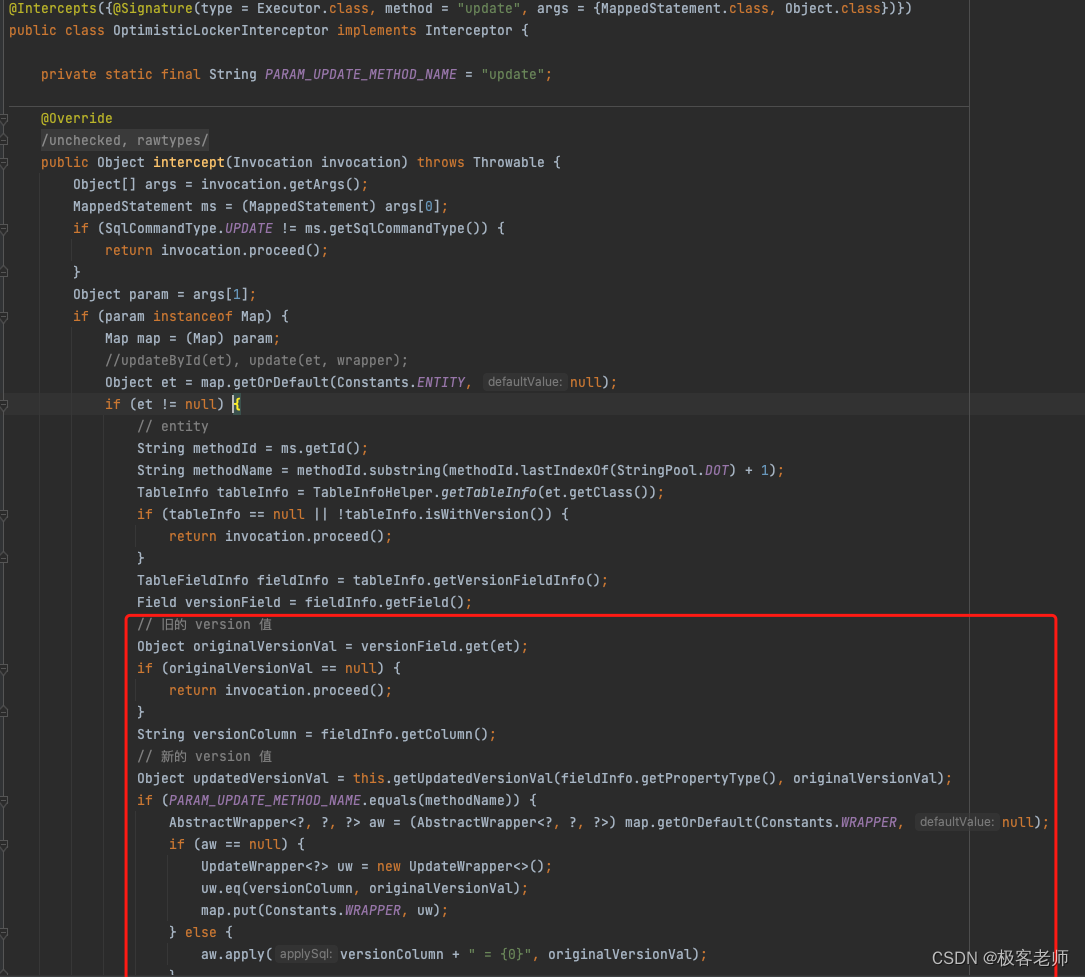
MyBatis-Plus为简化开发而生
简介 MyBatis-Plus 简称 MP是一个 MyBatis 的增强工具,在 MyBatis 的基础上只做增强不做改变,为简化开发、提高效率而生。 他们的愿景是成为 MyBatis 最好的搭档,就像魂斗罗中的 1P、2P,基友搭配,效率翻倍。 特性 无…...
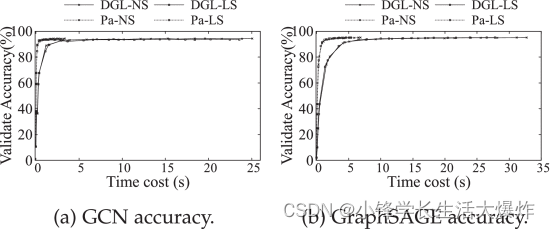
【翻译】Efficient Data Loader for Fast Sampling-Based GNN Training on Large Graphs
转载请注明出处:小锋学长生活大爆炸[xfxuezhang.cn] 此内容为机器翻译的结果,若有异议的地方,建议查看原文。 机器翻译的一些注意点,比如: 纪元、时代 > epoch工人 > worker火车、培训、训练师 > train Effic…...

OPUS解码器PLC
OPUS解码器支持PLC(Packet Loss Concealment)技术。 在音频通信中,网络丢包是常见的情况。当网络丢失一些音频数据包时,接收端可能无法正常解码并播放这些丢失的音频信号,导致声音中断或质量下降。为了改善这种情况&a…...
Rancher 使用指南
Rancher 使用指南 Rancher 是什么?Rancher 与 OpenShift / Kubesphere 主要区别对比RancherOpenShiftKubesphere 对比 Rancher 和 OpenShift Rancher 安装 Rancher 是什么? 企业级Kubernetes管理平台 Rancher 是供采用容器的团队使用的完整软件堆栈。它解决了管理多个Kuber…...

百度SEO优化全攻略(提高网站排名的5个方面)
百度SEO入门介绍: 随着互联网的不断发展,SEO已经成为网站优化的重要一环。而百度作为中国最大的搜索引擎,其SEO优化更是至关重要。SEO不仅能够提高网站排名,还能够提高网站流量、用户体验以及品牌知名度。因此,掌握百…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...
中的KV缓存压缩与动态稀疏注意力机制设计)
大语言模型(LLM)中的KV缓存压缩与动态稀疏注意力机制设计
随着大语言模型(LLM)参数规模的增长,推理阶段的内存占用和计算复杂度成为核心挑战。传统注意力机制的计算复杂度随序列长度呈二次方增长,而KV缓存的内存消耗可能高达数十GB(例如Llama2-7B处理100K token时需50GB内存&a…...

回溯算法学习
一、电话号码的字母组合 import java.util.ArrayList; import java.util.List;import javax.management.loading.PrivateClassLoader;public class letterCombinations {private static final String[] KEYPAD {"", //0"", //1"abc", //2"…...
:观察者模式)
JS设计模式(4):观察者模式
JS设计模式(4):观察者模式 一、引入 在开发中,我们经常会遇到这样的场景:一个对象的状态变化需要自动通知其他对象,比如: 电商平台中,商品库存变化时需要通知所有订阅该商品的用户;新闻网站中࿰…...

LINUX 69 FTP 客服管理系统 man 5 /etc/vsftpd/vsftpd.conf
FTP 客服管理系统 实现kefu123登录,不允许匿名访问,kefu只能访问/data/kefu目录,不能查看其他目录 创建账号密码 useradd kefu echo 123|passwd -stdin kefu [rootcode caozx26420]# echo 123|passwd --stdin kefu 更改用户 kefu 的密码…...

Unity中的transform.up
2025年6月8日,周日下午 在Unity中,transform.up是Transform组件的一个属性,表示游戏对象在世界空间中的“上”方向(Y轴正方向),且会随对象旋转动态变化。以下是关键点解析: 基本定义 transfor…...
