OPUS解码器PLC
OPUS解码器支持PLC(Packet Loss Concealment)技术。
在音频通信中,网络丢包是常见的情况。当网络丢失一些音频数据包时,接收端可能无法正常解码并播放这些丢失的音频信号,导致声音中断或质量下降。为了改善这种情况,音频编解码器通常会使用PLC技术进行处理。
PLC技术是一种丢包补偿技术,用于在缺少部分音频数据包时生成合理的伪造音频数据来填充缺失的部分。通过PLC技术,解码器可以根据已有的音频数据和其它相关信息(如延迟、声学特性等)来预测并生成丢失音频数据的替代值,以保证连续的音频播放。
OPUS编解码器在设计上就考虑了对网络丢包的容错性,并且内置了PLC功能。当OPUS解码器检测到音频数据包丢失时,它会自动使用PLC技术进行处理,生成适当的补偿音频数据,以确保音频的连续性和质量。
需要注意的是,PLC技术虽然可以在一定程度上改善丢包带来的音频中断问题,但其生成的补偿音频并非原始音频数据,因此无法完全还原丢失的部分。实际应用中,为了最大程度地减少音频丢失和改善音频质量,还应该结合使用其他技术,例如前向纠错(Forward Error Correction)和丢包重传等。
OPUS解码器支持PLC技术,可以在网络丢包情况下生成合理的补偿音频数据,以提供连续的音频播放和改善音频质量。
相关文章:

OPUS解码器PLC
OPUS解码器支持PLC(Packet Loss Concealment)技术。 在音频通信中,网络丢包是常见的情况。当网络丢失一些音频数据包时,接收端可能无法正常解码并播放这些丢失的音频信号,导致声音中断或质量下降。为了改善这种情况&a…...
Rancher 使用指南
Rancher 使用指南 Rancher 是什么?Rancher 与 OpenShift / Kubesphere 主要区别对比RancherOpenShiftKubesphere 对比 Rancher 和 OpenShift Rancher 安装 Rancher 是什么? 企业级Kubernetes管理平台 Rancher 是供采用容器的团队使用的完整软件堆栈。它解决了管理多个Kuber…...

百度SEO优化全攻略(提高网站排名的5个方面)
百度SEO入门介绍: 随着互联网的不断发展,SEO已经成为网站优化的重要一环。而百度作为中国最大的搜索引擎,其SEO优化更是至关重要。SEO不仅能够提高网站排名,还能够提高网站流量、用户体验以及品牌知名度。因此,掌握百…...

华为云云耀云服务器L实例评测|华为云耀云服务器L实例私有库搭建verdaccio(八)
九、华为云耀云服务器L实例私有库搭建verdaccio: Verdaccio 是一个简单的、零配置本地私有 npm 软件包代理注册表。Verdaccio 开箱即用,拥有自己的小型数据库,能够代理其它注册表(例如 npmjs.org),缓存下载…...
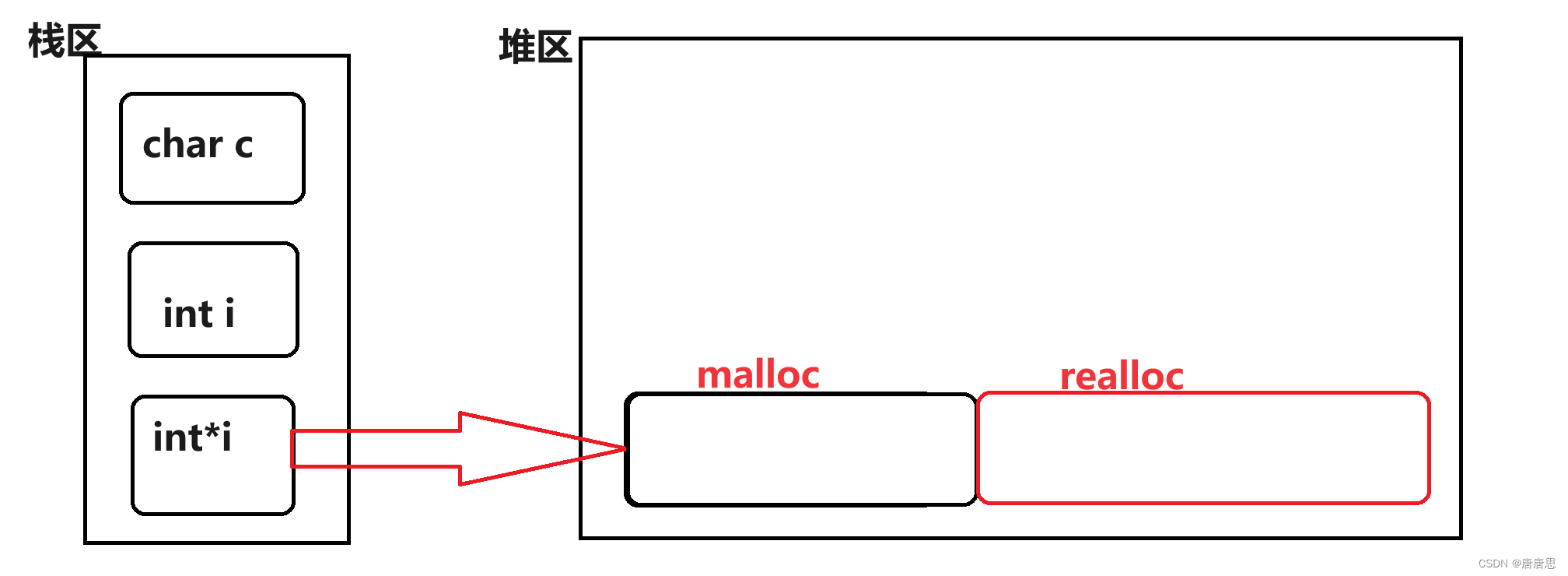
C语言之动态内存管理_柔性数组篇(2)
目录 柔性数组的特点 柔性数组的使用 动态内存函数增容柔性数组模拟实现 柔性数组的优势 今天接着来讲解一下柔性数组知识。 柔性数组的特点 C99中,结构中的最后一个元素允许是未知大小的数组,这就叫做【柔性数组】成员。 结构体中最后一个成员未…...

vue基础
引入vue文件 <div id"app"><!--{{}}插值表达式,绑定vue中的data数据-->{{message}} </div><script src"vue.min.js"></script> <script>new Vue({el:#app,data:{message:Hello Vue}}) </script>单项…...
访问量突破1W,纪念一下~
Mr.kanglong, 继续加油!...
)
C# 处理TCP数据的类(服务端)
using System; using System.Collections.Generic; using System.Net; using System.Net.Sockets; using System.Threading;namespace TestDemo {/// <summary>/// 处理TCP数据的类(服务端)/// </summary>public class TcpService{/// <s…...
【Jenkins】调用API构建并钉钉通知
文章目录 Jenkins API介绍提交作业带参数的作业API 令牌 Shell调用代码 Jenkins API介绍 Jenkins 提供了远程访问 API。目前它有三种格式: XML JSON Python 远程访问 API 形式为"…/api/" 例如, Jenkins 安装位于https://ci.jenkins.io&a…...

Java NIO三大核心组件
文章目录 一、Buffer1、重要属性2、重要方法1)allocate()创建缓冲区2)put()写入到缓冲区3)flip()翻转4)get()从缓冲区读取5)rewind()倒带6)mark()和reset()7)clear()清空缓冲区8)使用…...
?)
js数据排序方法(sort)?
在JavaScript中,可以使用Array的sort()方法对数据进行排序。下面是一个基本的例子,它展示了如何对一个数组进行升序和降序排序: // 创建一个数字数组 let numbers [2, 9, 1, 5, 8, 6];// 升序排序 let ascending numbers.sort(function(a,…...

若依框架学习笔记_mybatis
一、 在框架中引用的先后顺序 在ruoyi-system的resources下的xml中定义方法在java下的mapper包中引用方法在java下的service包中再引用mapper的方法 二、xml中的写法 标签: resultMap 返回数据sql 查询语句 可包含在其他操作中select 查询insert 插入update 更新…...

虚拟机的发展史:从分时系统到容器化
一、前世 早期计算机的价格非常昂贵,一台计算机可能需要花费几十万甚至上百万美元。例如,ENIAC计算机,作为世界上第一台通用电子数字计算机,当时的造价约为48万美元。科学家或者工程师们需要计算机的能力,但是买不起整…...

季涨约3~8%,DRAM合约价大幅回升 | 百能云芯
据TrendForce的研究显示,第4季DRAM与NAND Flash均价将开始全面上涨。特别是DRAM,预计第4季的合约价将季涨幅约在3%到8%之间。然而,这波上涨是否能持续,取决于供应商是否坚守减产策略以及实际需求的回升程度,尤其值得关…...

LocalDate的用法
日期时间转换 2023-03-30 14:25:00.000 DateTimeFormat(pattern "yyyy-MM-dd HH:mm:ss:sss")private LocalDateTime requestTimeStamp; 2021-06-18T10:46:19.67378508:00 new SimpleDateFormat("yyyy-MM-ddTHH:mm:ss:sssXXX");yyyy-mm-dd hh:mm:ss.sss 05…...

React通过ref获取子组件的数据和方法
父组件 1) ref必须传值, 否则childRef拿不到子组件的数据和方法 注意: 不一定使用app组件, 其他的任何父组件都可以 import "./App.css"; import React, { useEffect, useRef } from "react"; import RefToGetChild from "./components/RefToGetCh…...

Enhancing Self-Consistency and Performance of Pre-Trained Language Model
本文是LLM系列文章,针对《Enhancing Self-Consistency and Performance of Pre-Trained Language Models through Natural Language Inference》的翻译。 通过自然语言推理增强预训练语言模型的自一致性和性能 摘要1 引言2 相关工作3 通过关系检测进行一致性校正4 …...
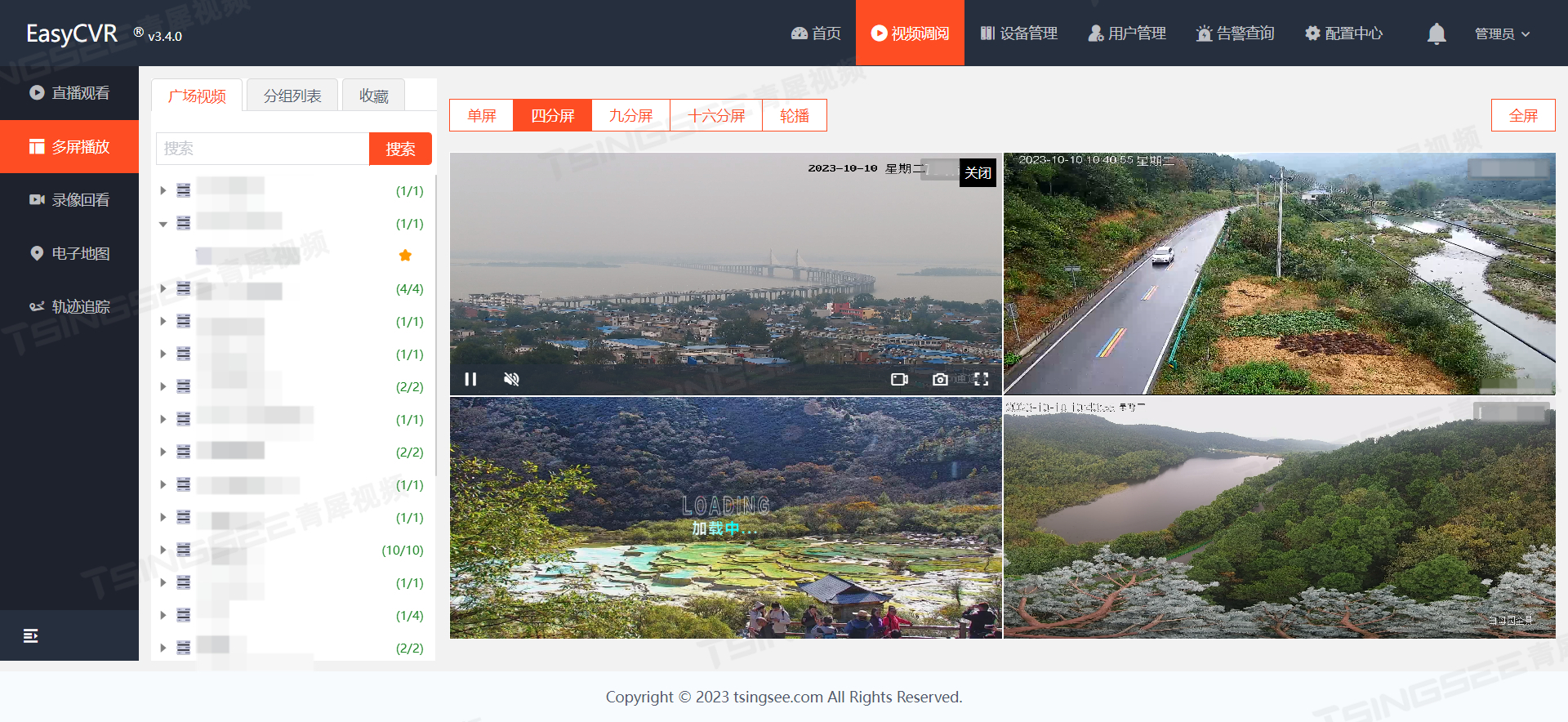
安防监控视频汇聚平台EasyCVR视频广场搜索异常,报错“通道未开启”的问题排查与解决
安防视频监控系统EasyCVR视频汇聚平台可拓展性强、视频能力灵活、部署轻快,可支持的主流标准协议有国标GB28181、RTSP/Onvif、RTMP等,以及厂家私有协议与SDK接入,包括海康Ehome、海大宇等设备的SDK等,能对外分发RTSP、RTMP、FLV、…...

css 星星闪烁加载框
今天带来的是普灵普灵的loader闪烁加载框 效果如下 开源精神给我们带来了源码 ,源码如下 <!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, in…...

代码随想录算法训练营第二十二天丨 二叉树part09
669. 修剪二叉搜索树 思路 递归法 从图中可以看出需要重构二叉树,想想是不是本题就有点复杂了。 其实不用重构那么复杂。 在上图中我们发现节点0并不符合区间要求,那么将节点0的右孩子 节点2 直接赋给 节点3的左孩子就可以了(就是把节点…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

优选算法第十二讲:队列 + 宽搜 优先级队列
优选算法第十二讲:队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...

React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store: 我们在使用异步的时候理应是要使用中间件的,但是configureStore 已经自动集成了 redux-thunk,注意action里面要返回函数 import { configureS…...

AI病理诊断七剑下天山,医疗未来触手可及
一、病理诊断困局:刀尖上的医学艺术 1.1 金标准背后的隐痛 病理诊断被誉为"诊断的诊断",医生需通过显微镜观察组织切片,在细胞迷宫中捕捉癌变信号。某省病理质控报告显示,基层医院误诊率达12%-15%,专家会诊…...

C++:多态机制详解
目录 一. 多态的概念 1.静态多态(编译时多态) 二.动态多态的定义及实现 1.多态的构成条件 2.虚函数 3.虚函数的重写/覆盖 4.虚函数重写的一些其他问题 1).协变 2).析构函数的重写 5.override 和 final关键字 1&#…...

打手机检测算法AI智能分析网关V4守护公共/工业/医疗等多场景安全应用
一、方案背景 在现代生产与生活场景中,如工厂高危作业区、医院手术室、公共场景等,人员违规打手机的行为潜藏着巨大风险。传统依靠人工巡查的监管方式,存在效率低、覆盖面不足、判断主观性强等问题,难以满足对人员打手机行为精…...
