代码随想录算法训练营第二十二天丨 二叉树part09
669. 修剪二叉搜索树
思路
递归法
从图中可以看出需要重构二叉树,想想是不是本题就有点复杂了。
其实不用重构那么复杂。
在上图中我们发现节点0并不符合区间要求,那么将节点0的右孩子 节点2 直接赋给 节点3的左孩子就可以了(就是把节点0从二叉树中移除),如图:

理解了最关键部分了我们再递归三部曲:
- 确定递归函数的参数以及返回值
这里我们为什么需要返回值呢?
因为是要遍历整棵树,做修改,其实不需要返回值也可以,我们也可以完成修剪(其实就是从二叉树中移除节点)的操作。
但是有返回值,更方便,可以通过递归函数的返回值来移除节点。
这样的做法在二叉树:搜索树中的插入操作 (opens new window)和二叉树:搜索树中的删除操作 (opens new window)中大家已经了解过了。
代码如下:
TreeNode trimNode(TreeNode cur, int low, int high)
- 确定终止条件
修剪的操作并不是在终止条件上进行的,所以就是遇到空节点返回就可以了。
if (cur == null){return null;
}- 确定单层递归的逻辑
如果root(当前节点)的元素小于low的数值,那么应该递归右子树,并返回右子树符合条件的头结点。
代码如下:
// 寻找符合区间[low, high]的节点
if (cur.val < low){TreeNode right = trimNode(cur.right, low, high);return right;
}如果root(当前节点)的元素大于high的,那么应该递归左子树,并返回左子树符合条件的头结点。
代码如下:
if (cur.val > high){TreeNode left = trimNode(cur.left,low,high);return left;
}接下来要将下一层处理完左子树的结果赋给root->left,处理完右子树的结果赋给root->right。
最后返回root节点,代码如下:
cur.left = trimNode(cur.left,low,high);//cur.left接入符合条件的左孩子
cur.right = trimNode(cur.right,low,high);//cur.right接入符合条件的右孩子
return cur;此时大家是不是还没发现这多余的节点究竟是如何从二叉树中移除的呢?
在回顾一下上面的代码,针对下图中二叉树的情况:
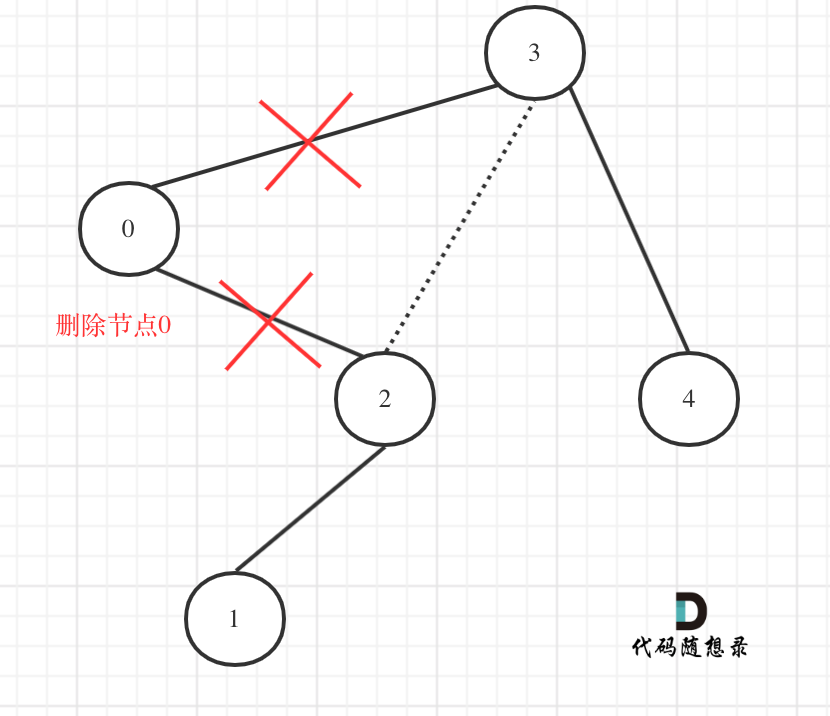
如下代码相当于把节点0的右孩子(节点2)返回给上一层,
// 寻找符合区间[low, high]的节点
if (cur.val < low){TreeNode right = trimNode(cur.right, low, high);return right;
}
然后如下代码相当于用节点3的左孩子 把下一层返回的 节点0的右孩子(节点2) 接住。
cur.left = trimNode(cur.left,low,high);//cur.left接入符合条件的左孩子此时节点3的左孩子就变成了节点2,将节点0从二叉树中移除了。
整体代码如下:
class Solution {public TreeNode trimBST(TreeNode root, int low, int high) {return trimNode(root,low,high);}TreeNode trimNode(TreeNode cur, int low, int high){if (cur == null){return null;}// 寻找符合区间[low, high]的节点if (cur.val < low){TreeNode right = trimNode(cur.right, low, high);return right;}if (cur.val > high){TreeNode left = trimNode(cur.left,low,high);return left;}cur.left = trimNode(cur.left,low,high);//cur.left接入符合条件的左孩子cur.right = trimNode(cur.right,low,high);//cur.right接入符合条件的右孩子return cur;}
}108.将有序数组转换为二叉搜索树
思路
题目中说要转换为一棵高度平衡二叉搜索树。为什么强调要平衡呢?
因为只要给我们一个有序数组,如果强调平衡,都可以以线性结构来构造二叉搜索树。
例如 有序数组[-10,-3,0,5,9] 就可以构造成这样的二叉搜索树,如图。

上图中,是符合二叉搜索树的特性吧,如果要这么做的话,是不是本题意义就不大了,所以才强调是平衡二叉搜索树。
其实数组构造二叉树,构成平衡树是自然而然的事情,因为大家默认都是从数组中间位置取值作为节点元素,一般不会随机取。所以想构成不平衡的二叉树是自找麻烦。
本质就是寻找分割点,分割点作为当前节点,然后递归左区间和右区间。
分割点就是数组中间位置的节点。
那么为问题来了,如果数组长度为偶数,中间节点有两个,取哪一个?
取哪一个都可以,只不过构成了不同的平衡二叉搜索树。
例如:输入:[-10,-3,0,5,9]
如下两棵树,都是这个数组的平衡二叉搜索树:

如果要分割的数组长度为偶数的时候,中间元素为两个,是取左边元素 就是树1,取右边元素就是树2。
递归
递归三部曲:
- 确定递归函数返回值及其参数
删除二叉树节点,增加二叉树节点,都是用递归函数的返回值来完成,这样是比较方便的。
相信大家如果仔细看了二叉树:搜索树中的插入操作 (opens new window)和二叉树:搜索树中的删除操作 (opens new window),一定会对递归函数返回值的作用深有感触。
那么本题要构造二叉树,依然用递归函数的返回值来构造中节点的左右孩子。
再来看参数,首先是传入数组,然后就是左下标left和右下标right,我们在二叉树:构造二叉树登场! (opens new window)中提过,在构造二叉树的时候尽量不要重新定义左右区间数组,而是用下标来操作原数组。
所以代码如下:
// 左闭右闭区间[left, right]
TreeNode sortTree(int[] nums,int left,int right)
这里注意,我这里定义的是左闭右闭区间,在不断分割的过程中,也会坚持左闭右闭的区间,这又涉及到我们讲过的循环不变量。
- 确定递归终止条件
这里定义的是左闭右闭的区间,所以当区间 left > right的时候,就是空节点了。
代码如下:
if (left > right){return null;}
- 确定单层递归的逻辑
首先取数组中间元素的位置,不难写出int mid = (left + right) / 2;,这么写其实有一个问题,就是数值越界,例如left和right都是最大int,这么操作就越界了,在二分法 (opens new window)中尤其需要注意!
所以可以这么写:int mid = left + ((right - left) / 2);
但本题leetcode的测试数据并不会越界,所以怎么写都可以。但需要有这个意识!
取了中间位置,就开始以中间位置的元素构造节点,代码:TreeNode cur = new TreeNode(nums[mid]); 。
接着划分区间,root的左孩子接住下一层左区间的构造节点,右孩子接住下一层右区间构造的节点。
最后返回root节点,单层递归整体代码如下:
int mid = (left+right) /2;
TreeNode cur = new TreeNode(nums[mid]);
cur.left = sortTree(nums,left,mid-1);
cur.right = sortTree(nums,mid+1,right);
return cur;- 递归整体代码如下:
class Solution {public TreeNode sortedArrayToBST(int[] nums) {return sortTree(nums,0, nums.length-1);}// 左闭右闭区间[left, right]TreeNode sortTree(int[] nums,int left,int right){if (left > right){return null;}int mid = (left+right) /2;TreeNode cur = new TreeNode(nums[mid]);cur.left = sortTree(nums,left,mid-1);cur.right = sortTree(nums,mid+1,right);return cur;}
}538.把二叉搜索树转换为累加树
思路
如何累加?遇到一个节点,然后再遍历其他节点累加?
然后再发现这是一棵二叉搜索树,二叉搜索树啊,这是有序的啊。
那么有序的元素如何求累加呢?
其实这就是一棵树,大家可能看起来有点别扭,换一个角度来看,这就是一个有序数组[2, 5, 13],求从后到前的累加数组,也就是[20, 18, 13],是不是感觉这就简单了。
为什么变成数组就是感觉简单了呢?
因为数组大家都知道怎么遍历啊,从后向前,挨个累加就完事了,这换成了二叉搜索树,看起来就别扭了一些是不是。
那么知道如何遍历这个二叉树,也就迎刃而解了,从树中可以看出累加的顺序是右中左,所以我们需要反中序遍历这个二叉树,然后顺序累加就可以了。
#递归
遍历顺序如图所示:

本题依然需要一个pre指针记录当前遍历节点cur的前一个节点,这样才方便做累加。
pre指针的使用技巧,在二叉树:搜索树的最小绝对差 (opens new window)和二叉树:我的众数是多少? (opens new window)都提到了,这是常用的操作手段。
- 递归函数参数以及返回值
这里很明确了,不需要递归函数的返回值做什么操作了,要遍历整棵树。
同时需要定义一个全局变量pre,用来保存cur节点的前一个节点的数值。
代码如下:
// 记录前一个节点的数值
TreeNode pre = new TreeNode(0);- 确定终止条件
遇空就终止。
if (node == null){return null;
}- 确定单层递归的逻辑
注意要右中左来遍历二叉树, 中节点的处理逻辑就是让cur的数值加上前一个节点的数值。
代码如下:
//右
sumTree(node.right);
//中
node.val = node.val + pre.val;
pre = node;
//左
sumTree(node.left);return node;
递归法整体代码如下:
class Solution {public TreeNode convertBST(TreeNode root) {return sumTree(root);}// 记录前一个节点的数值TreeNode pre = new TreeNode(0);//右中左TreeNode sumTree(TreeNode node){if (node == null){return null;}//右sumTree(node.right);//中node.val = node.val + pre.val;pre = node;//左sumTree(node.left);return node;}
}以上为我做题时候的相关思路,自己的语言组织能力较弱,很多都是直接抄卡哥的,有错误望指正。
相关文章:

代码随想录算法训练营第二十二天丨 二叉树part09
669. 修剪二叉搜索树 思路 递归法 从图中可以看出需要重构二叉树,想想是不是本题就有点复杂了。 其实不用重构那么复杂。 在上图中我们发现节点0并不符合区间要求,那么将节点0的右孩子 节点2 直接赋给 节点3的左孩子就可以了(就是把节点…...
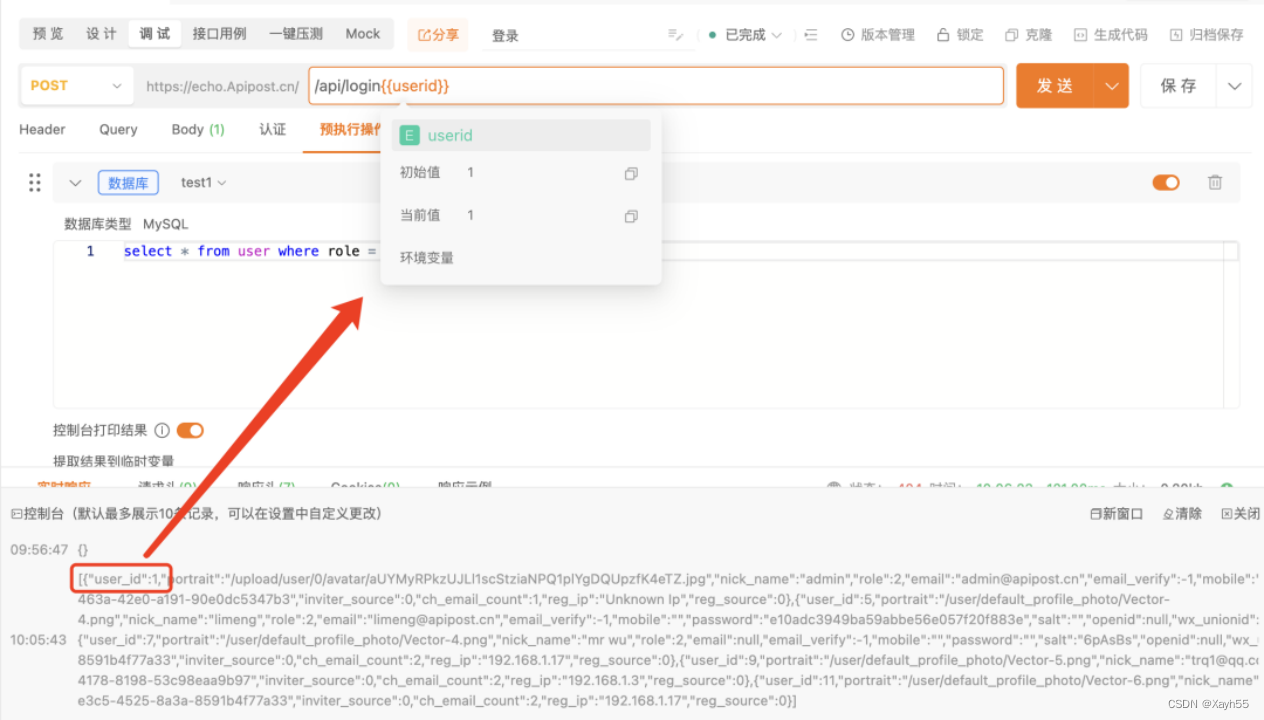
Apipost连接数据库详解
Apipost提供了数据库连接功能,在接口调试时可以使用数据库获取入参或进行断言校验。目前的Apipost支持:Mysql、SQL Sever、Oracle、Clickhouse、达梦数据库、PostgreSQL、Redis、MongoDB 8种数据库的连接操作 新建数据库连接: 在「项目设置…...
让 Visual Studio 用上 ChatGPT
一、简介 Visual chatGPT Studio 是 Visual Studio 的一个免费扩展,它直接在 IDE 中添加了 chatGPT 功能。它允许用户以可以根据菜单功能的方式使用 chatGPT。 二、功能介绍 该扩展提供了一组使用 ChatGPT 命令,可以在编辑器中选择你需要处理的代码或…...

如何删除错误堆栈里的数据
修改某个主数据。然后发现N年前,某位开发在DTP上做了一个错误堆栈。 这里面有很多历史错误信息,有几千条了,一条条删肯定不可能。 如果不删除,DTP增量无法激活,明天处理链肯定出问题。 于是找到一位印度大神的方法&a…...

k8s使用minio分布式集群作为存储--基础配置篇
背景:minio分布式集群是单独的服务,并没有被k8s管理,k8s与minio集群在不同的服务器上部署,k8s需要使用minio分布式集群作为k8s集群的配置文件及其他文件的存储介质。 1、安装fuse: sudo yum install fuse1.1查询是否有fusemount3 sudo find / -name fusermount31.2确认…...
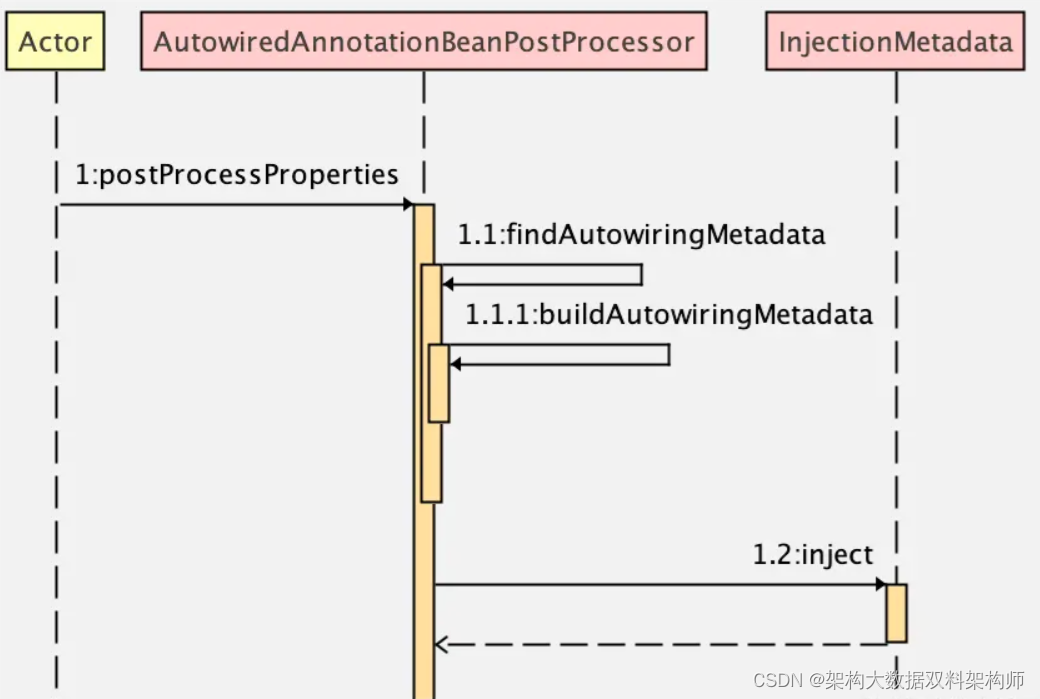
@Autowired 到底是怎么把变量注入进来的?
[toc] 在 Spring 容器中,当我们想给某一个属性注入值的时候,有多种不同的方式,例如可以通过构造器注入、可以通过 set 方法注入,也可以使用 Autowired、Inject、Resource 等注解注入。 今天我就来和小伙伴们聊一聊,Au…...

【Python学习笔记】函数
1. 函数组成 Python中,我们是这样定义函数的: def function(para1, para2):print("func start")print(para1)print(para2)print("func end")print("让技术总监面试 求职者")return "func return"def 是关键字…...

简单实现一个todoList(上移、下移、置顶、置底)
演示 html部分 <!DOCTYPE html> <html> <head><title>表格示例</title> </head> <body><table border"1"><thead><tr><th>更新时间</th><th>操作</th></tr></thead…...

计算机视觉:池化层的作用是什么?
本文重点 在深度学习中,卷积神经网络(CNN)是一种非常强大的模型,广泛应用于图像识别、目标检测、自然语言处理等领域。而池化层作为CNN中的一个关键步骤,扮演着优化神经网络、提升深度学习性能的重要角色。本文将深入探讨池化层的作用及其重要性,帮助读者更好地理解和应…...

luffy项目前端创建、配置、解决跨域问题、后端数据库迁移
前端 创建前端vue 使用vue-cil创建前端将无用的东西删除 配置 跟后端交互:axios 安装插件:cnpm install -S axios在main.js中写import axios from "axios"; Vue.prototype.$axios axios后续使用就直接this.$axios即可 操作cookie&am…...

电商数据API接口:新服务下电商网站、跨境电商独立站,移动APP的新型拉新武器
互联网的发展改变了我们的生活方式,也改变了企业商家们的营销方式,越来越多的企业商家把产品营销从线下转到线上,选择在线商城、移动APP、微信公众号等互联网工具进行营销活动。而随着营销模式的多元化和电子支付渠道的进一步发展,…...

多线程并发篇---第十一篇
系列文章目录 文章目录 系列文章目录前言一、CAS的原理二、CAS有什么缺点吗?三、引用类型有哪些?有什么区别?前言 一、CAS的原理 CAS叫做CompareAndSwap,比较并交换,主要是通过处理器的指令来保证操作的原子性,它包含 三个操作数: 变量内存地址,V表示旧的预期值,A表示…...

JVM第六讲:JVM 基础 - Java 内存模型引入
JVM 基础 - Java 内存模型引入 很多人都无法区分Java内存模型和JVM内存结构,以及Java内存模型与物理内存之间的关系。本文是JVM第六讲,从堆栈角度引入JMM,然后介绍JMM和物理内存之间的关系, 为后面JMM详解, JVM 内存结构详解, Java 对象模型详…...

机房安全管理制度
#安全运维管理制度# 1、总则 1.1、目的 为进一步规范XXXXX单位机房安全管理工作,防止未经授权的访问,做好机房的防火、防盗等工作,确保XXXXX单位机房物理设施的安全,制定本制度。 1.2、范围 本制度适用于XXXXX单位机房的安全…...
【自然语言处理】— 隐马尔可夫模型详解、例解
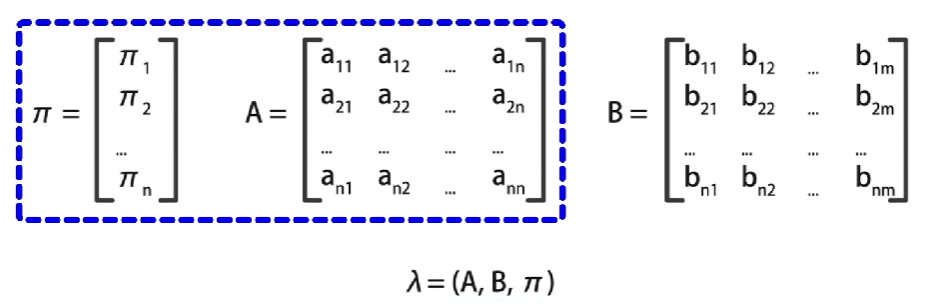
【自然语言处理】— 隐马尔可夫模型 【自然语言处理】— 隐马尔可夫模型引例隐马尔可夫模型概念隐马尔可夫模型的关键隐马尔可夫模型的数学表示隐含状态与观测结果状态转移矩阵观测概率矩阵初始状态概率向量 小结 【自然语言处理】— 隐马尔可夫模型 引例 假设有三种不同的骰…...

运行的 akrun 会打印信息到控制台,如何取消打印 -- chatGPT
gpt: 如果运行的程序 akrun 打印信息到控制台,但您希望取消或禁止它的输出,可以尝试以下方法: 1. **重定向输出到空文件**:您可以将程序的标准输出重定向到一个空文件,从而禁止信息输出到控制台。执行以下命令&#…...

【React】03-React面向组件编程2
文章目录 2.6. 组件的生命周期2.6.1. 效果2.6.2. 理解2.6.3. 生命周期流程图(旧)2.6.4. 生命周期流程图(新)2.6.5. 重要的勾子2.6.6. 即将废弃的勾子2.6.7 getSnapshotBeforeUpdate 2.7. 虚拟DOM与DOM Diffing算法2.7.1. 效果2.7.2. 基本原理图 2.6. 组件的生命周期 2.6.1. 效…...

【python编程】python无法import模块的一种原因分析
python系统路径添加错误 报错原因原因分析解决办法补充 最近写代码的时候遇到一个问题,就是想添加工程下fu_convert文件夹下自己编写的convert_fw.py模块,但是出现报错,是个比较低级的问题,但还是简单记录一下 报错原因 无法找到…...

vue3.0与vue2.0的区别
前言 Vue 3.0是一个用于构建用户界面的JavaScript框架。相比于Vue 2.x,Vue 3.0在性能、体积和开发体验上都有了很大的提升。 以下将从不同的角度上去分析Vue 3.0与Vue 2.0的区别: 一、项目架构 从项目搭建和打包工具的选择来看: Vue 2.0 中…...
09_Webpack打包工具
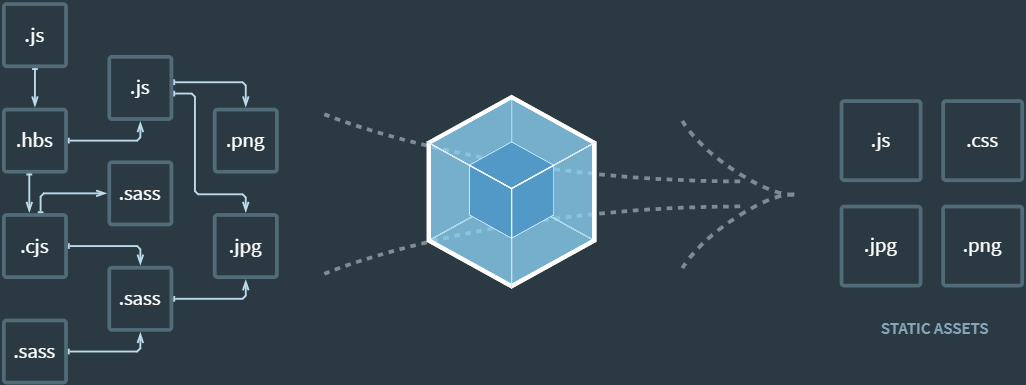
1 初识Webpack 1.1 什么是Webpack Webpack打包工具对项目中的复杂文件进行打包处理,可以实现项目的自动化构建,并且给前端开发人员带来了极大的便利。 目前,企业中的绝大多数前端项目是基于Webpack打包工具来进行开发的。 1.2 Webpack的安…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...

CSS | transition 和 transform的用处和区别
省流总结: transform用于变换/变形,transition是动画控制器 transform 用来对元素进行变形,常见的操作如下,它是立即生效的样式变形属性。 旋转 rotate(角度deg)、平移 translateX(像素px)、缩放 scale(倍数)、倾斜 skewX(角度…...

goreplay
1.github地址 https://github.com/buger/goreplay 2.简单介绍 GoReplay 是一个开源的网络监控工具,可以记录用户的实时流量并将其用于镜像、负载测试、监控和详细分析。 3.出现背景 随着应用程序的增长,测试它所需的工作量也会呈指数级增长。GoRepl…...

基于小程序老人监护管理系统源码数据库文档
摘 要 近年来,随着我国人口老龄化问题日益严重,独居和居住养老机构的的老年人数量越来越多。而随着老年人数量的逐步增长,随之而来的是日益突出的老年人问题,尤其是老年人的健康问题,尤其是老年人产生健康问题后&…...

新版NANO下载烧录过程
一、序言 搭建 Jetson 系列产品烧录系统的环境需要在电脑主机上安装 Ubuntu 系统。此处使用 18.04 LTS。 二、环境搭建 1、安装库 $ sudo apt-get install qemu-user-static$ sudo apt-get install python 搭建环境的过程需要这个应用库来将某些 NVIDIA 软件组件安装到 Je…...

初级程序员入门指南
初级程序员入门指南 在数字化浪潮中,编程已然成为极具价值的技能。对于渴望踏入程序员行列的新手而言,明晰入门路径与必备知识是开启征程的关键。本文将为初级程序员提供全面的入门指引。 一、明确学习方向 (一)编程语言抉择 编…...
