【自然语言处理】— 隐马尔可夫模型详解、例解
【自然语言处理】— 隐马尔可夫模型
- 【自然语言处理】— 隐马尔可夫模型
- 引例
- 隐马尔可夫模型概念
- 隐马尔可夫模型的关键
- 隐马尔可夫模型的数学表示
- 隐含状态与观测结果
- 状态转移矩阵
- 观测概率矩阵
- 初始状态概率向量
- 小结
【自然语言处理】— 隐马尔可夫模型
引例
假设有三种不同的骰子,分别是立方体,正四面体,正八面体,分别有1-6,1-4,1-8,分别记作D6、D4、D8。每个面出现的概率分别是1/6,1/4,1/8。
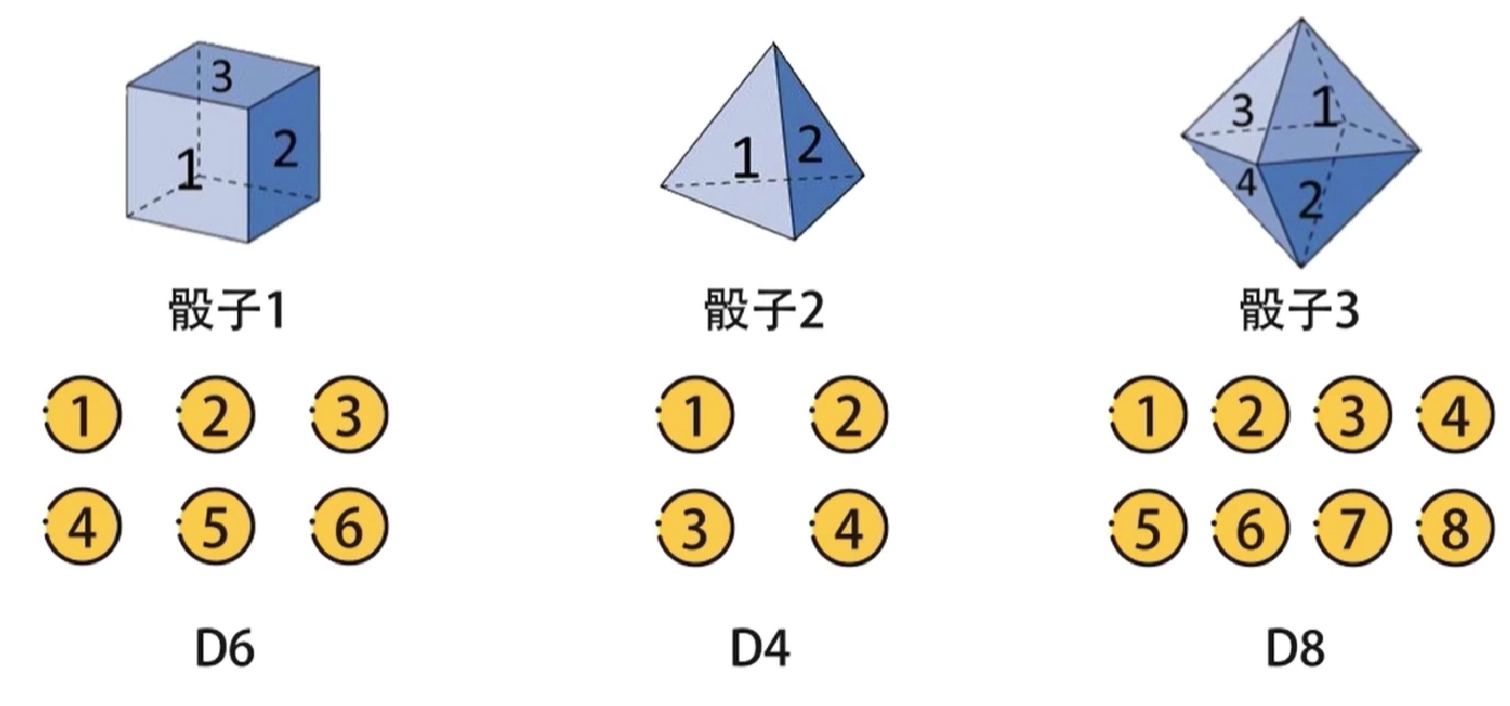
在不观察的情况下,从三个骰子中随机选一个,进行抛掷,结果可能是1-8中的任意数字。依照这种方式,随机选择骰子,重复抛掷,可以得到一串数字,这串数字对我们是可见的,并且直接记录下来了,因此将这串数字记作可见状态链

在抛掷的过程中,被我们随机选择的骰子编号也组成了一串序列,因为我们是随机选择的骰子,因此将这串序列称为隐含状态链
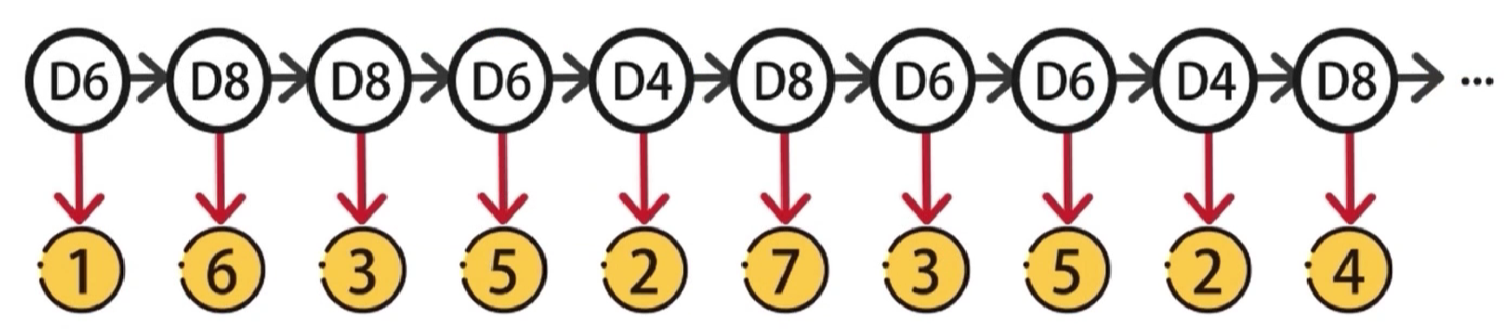
实验过程中产生了两个数据链,隐含状态链和可见状态链,隐马尔可夫模型=隐含状态链➕可见状态链
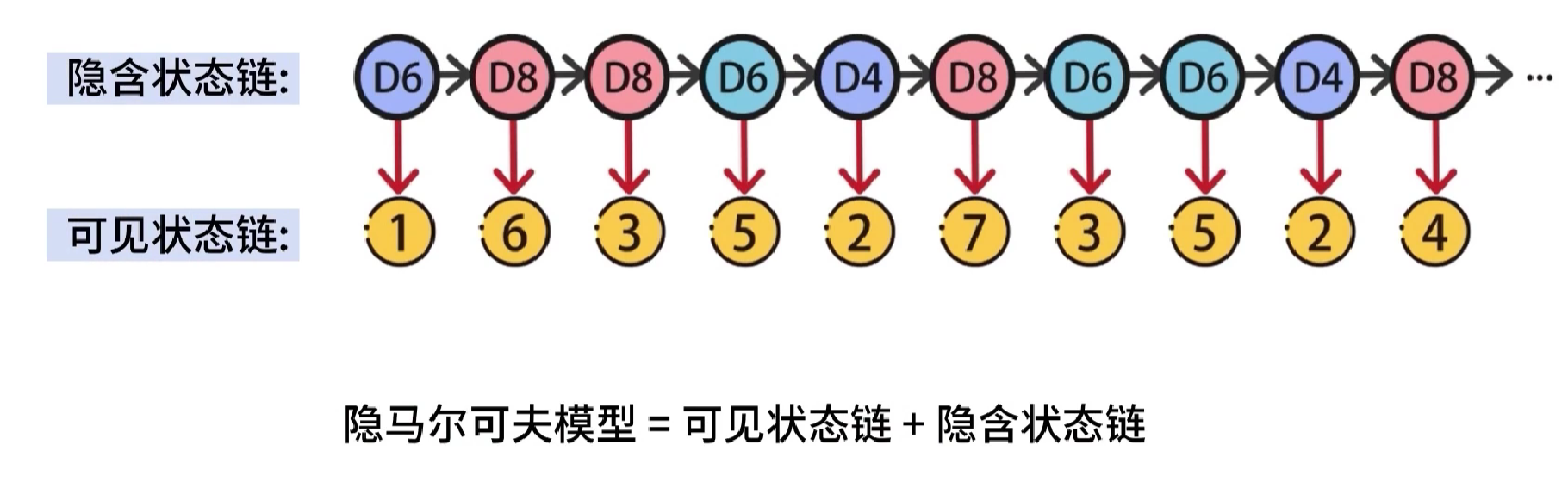
隐马尔可夫模型概念
隐马尔可夫模型(Hidden Markov Model),简称HMM,它是关于时序的概率模型,该模型包含随机生成的不可观测序列,该序列被称为状态序列,使用S表示,每个不可观测状态都会产生一个可观测的结果,这样会得到一个观测序列,使用O表示。
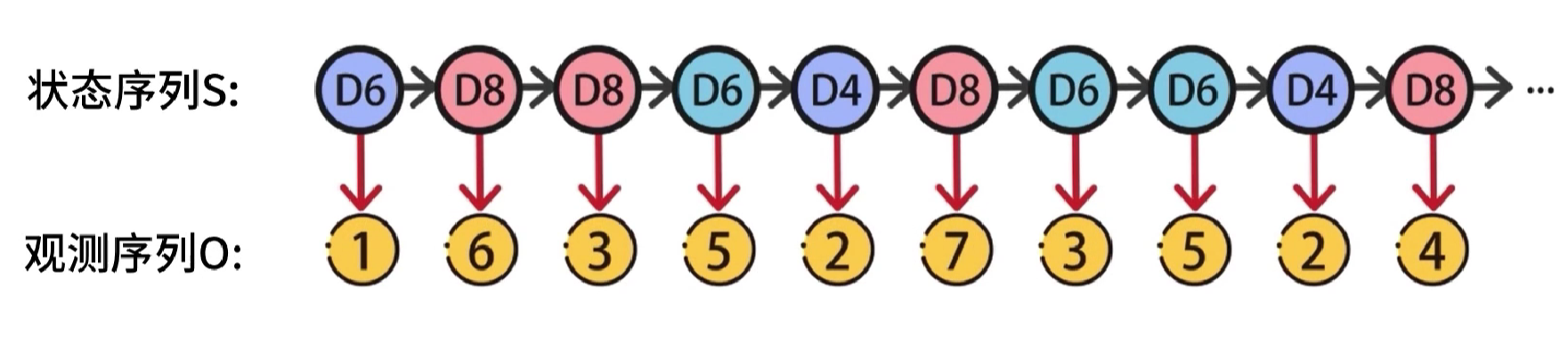
每个状态和时刻都会与一个时刻进行对应,如果有t个时刻,就产生了 s 1 → s t , o 1 → o t s_1→s_t,o_1→o_t s1→st,o1→ot,相当于一次一次掷骰子,t就代表第几次掷骰子
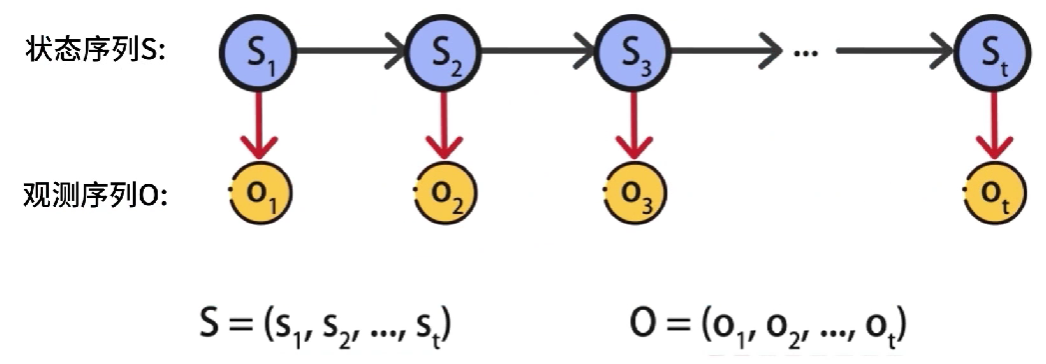
在HMM中,状态序列是隐藏的,无法被观测到,因此状态变量是一个隐变量,隐藏的状态序列是由一个马尔可夫链,随机生成的
隐马尔可夫模型的关键
在隐马尔可夫模型中, 包含了四个关键因素,分别是:
- 隐含状态
- 可见状态
- 隐含状态转换
- 可见状态输出
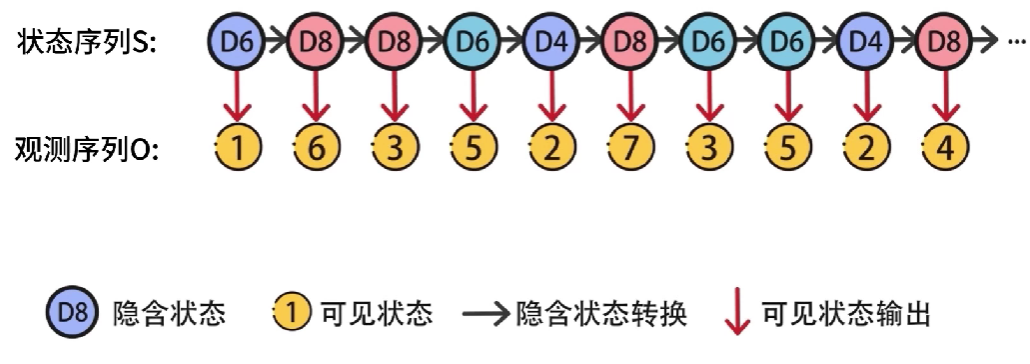
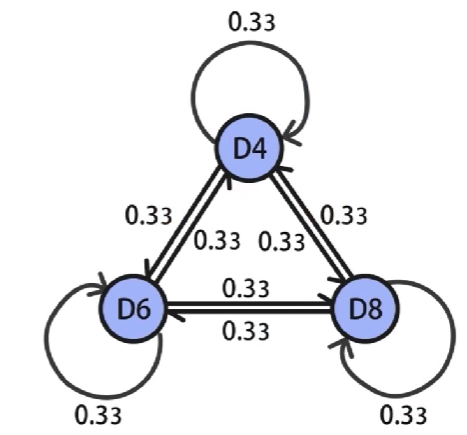
各个隐含状态之间会进行转换,存在着对应的转换概率
隐含状态会输出可见状态,隐含状态和可见状态之间有一个输出概率,不同隐含状态到可见状态的输出概率可能不同
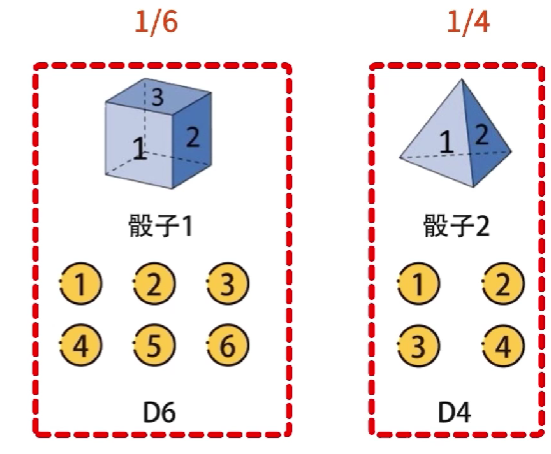
例如,隐含状态D6输出可见状态1到6概率是 1 6 \cfrac{1}{6} 61,隐含状态D4输出可见状态1到4概率是 1 4 \cfrac{1}{4} 41,
隐马尔可夫模型的数学表示
为了进一步讨论隐马尔可夫模型,需要使用数学符号来表示HMM,其中包括隐含状态 Q Q Q和观测结果 V V V两个集合,状态转移概率矩阵 A A A,观测概率矩阵 B B B,初始状态概率向量 π \pi π,三个概率矩阵。
隐含状态与观测结果
例如,隐含状态集合 Q = { q 1 , q 2 , . . . , q n } Q = \{q_1,q_2,...,q_n\} Q={q1,q2,...,qn}包括 q 1 到 q n n q_1到q_n n q1到qnn种状态
观测结果集合 V = { v 1 , v 2 , . . . , v m } V=\{v_1,v_2,...,v_m\} V={v1,v2,...,vm}包括 v 1 到 v m m v_1到v_m m v1到vmm种可能的结果
在掷骰子的案例中, n = 3 q 1 , q 2 , q 3 对应 D 6 , D 4 , D 8 n=3\ \ \ q_1,q_2,q_3对应D_6,D_4,D_8 n=3 q1,q2,q3对应D6,D4,D8
m = 8 v 1 到 v 8 对应数字 1 到 8 m=8 \ \ \ v_1到v_8对应数字1到8 m=8 v1到v8对应数字1到8

状态转移矩阵
状态转移的概率矩阵 A A A是一个是一个 N ∗ N N*N N∗N的矩阵
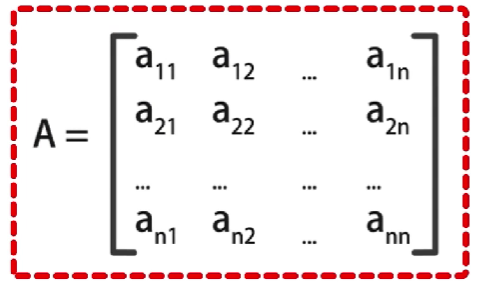
其中 a i j a_{ij} aij代表了状态 q i q_i qi转移到状态 q j q_j qj的概率
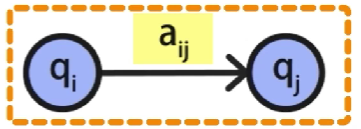
具体地, a i j 等于在 s t = q i 的条件下, s t + 1 = q j 的概率 a_{ij}等于在s_t = q_i的条件下,s_{t+1}=q_j的概率 aij等于在st=qi的条件下,st+1=qj的概率
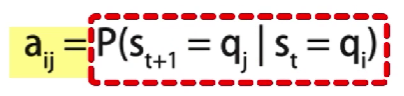
例如,3个骰子,选择任意骰子的概率都是 1 3 \cfrac{1}{3} 31,那么就得到了 3 ∗ 3 3*3 3∗3的状态转移概率矩阵,其中的每个元素都是 0.33 0.33 0.33,
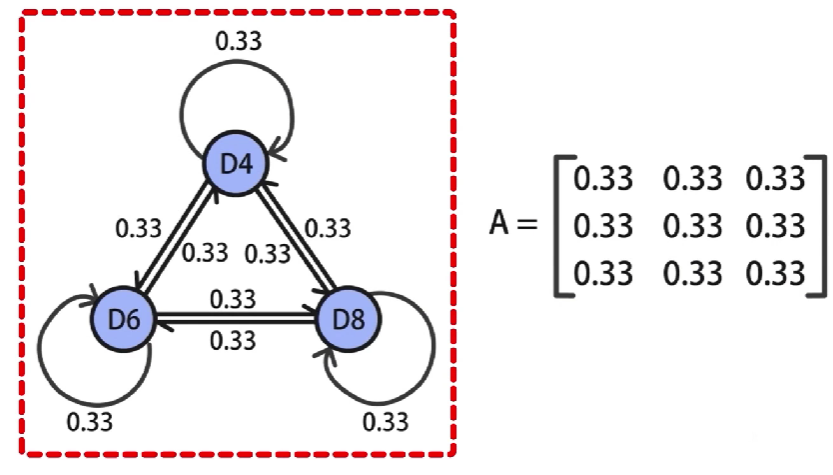
观测概率矩阵
观测概率矩阵为 B B B,由于每一个状态 q q q都可以输出一个观测结果 v v v,因此B是一个 N ∗ M N*M N∗M的矩阵
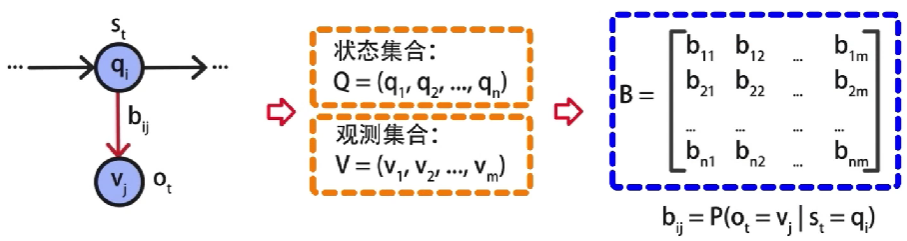
其中 b i j b_ij bij代表了在时刻 t t t,状态 q i q_i qi输出观测结果 v j v_j vj的概率。
例如,在掷骰子时,根据三种骰子的输出,可以得到一个 3 ∗ 8 3*8 3∗8的概率矩阵,第一行对应六面骰子,输出1到6的概率是1/6,输出7和8的概率是0,而第二行和第三行,分别代表投掷四面骰子和八面骰子的输出1到8的概率
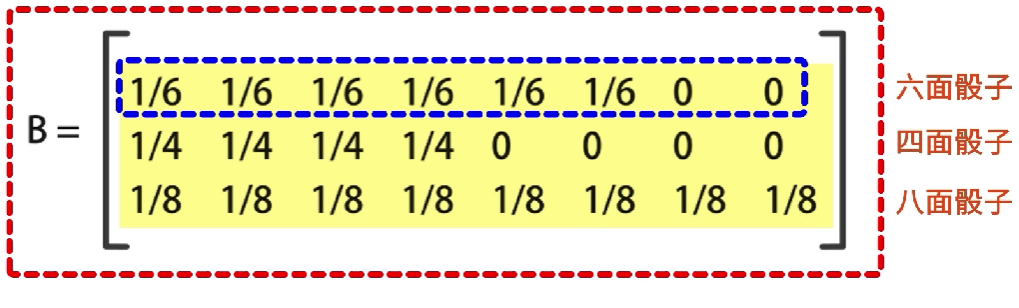
初始状态概率向量
初始状态的概率向量是 π \pi π,它是一个 N ∗ 1 N*1 N∗1的列向量, π i \pi_i πi代表在时刻 t = 1 t=1 t=1时,状态为 q i q_i qi的概率,例如,掷骰子时,三种骰子的概率都是1/3

小结
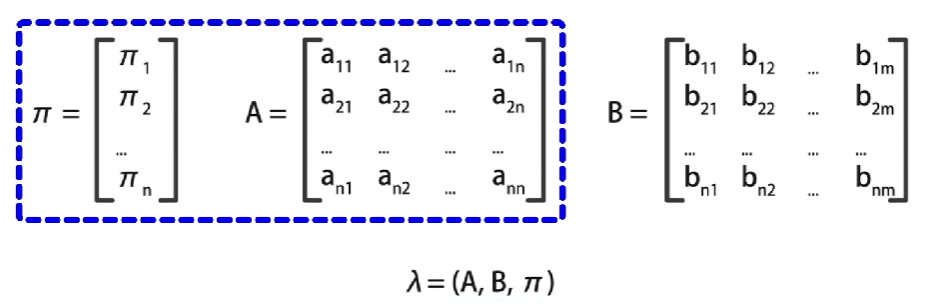
π 和 A \pi和A π和A确定了隐藏的马尔可夫链,也就是如何生成不可观测的状态序列 S S S, B B B确定了如何从隐藏状态产生观测状态序列 O O O,隐马尔可夫模型由 A 、 B 、 π A、B、\pi A、B、π共同决定,使用三元符号 λ = ( A , B , π ) λ=(A,B,\pi) λ=(A,B,π)表示。
参考视频:什么是HMM隐马尔可夫模型,自然语言处理中的最基础算法之一_哔哩哔哩_bilibili
相关文章:

【自然语言处理】— 隐马尔可夫模型详解、例解
【自然语言处理】— 隐马尔可夫模型 【自然语言处理】— 隐马尔可夫模型引例隐马尔可夫模型概念隐马尔可夫模型的关键隐马尔可夫模型的数学表示隐含状态与观测结果状态转移矩阵观测概率矩阵初始状态概率向量 小结 【自然语言处理】— 隐马尔可夫模型 引例 假设有三种不同的骰…...

运行的 akrun 会打印信息到控制台,如何取消打印 -- chatGPT
gpt: 如果运行的程序 akrun 打印信息到控制台,但您希望取消或禁止它的输出,可以尝试以下方法: 1. **重定向输出到空文件**:您可以将程序的标准输出重定向到一个空文件,从而禁止信息输出到控制台。执行以下命令&#…...

【React】03-React面向组件编程2
文章目录 2.6. 组件的生命周期2.6.1. 效果2.6.2. 理解2.6.3. 生命周期流程图(旧)2.6.4. 生命周期流程图(新)2.6.5. 重要的勾子2.6.6. 即将废弃的勾子2.6.7 getSnapshotBeforeUpdate 2.7. 虚拟DOM与DOM Diffing算法2.7.1. 效果2.7.2. 基本原理图 2.6. 组件的生命周期 2.6.1. 效…...

【python编程】python无法import模块的一种原因分析
python系统路径添加错误 报错原因原因分析解决办法补充 最近写代码的时候遇到一个问题,就是想添加工程下fu_convert文件夹下自己编写的convert_fw.py模块,但是出现报错,是个比较低级的问题,但还是简单记录一下 报错原因 无法找到…...

vue3.0与vue2.0的区别
前言 Vue 3.0是一个用于构建用户界面的JavaScript框架。相比于Vue 2.x,Vue 3.0在性能、体积和开发体验上都有了很大的提升。 以下将从不同的角度上去分析Vue 3.0与Vue 2.0的区别: 一、项目架构 从项目搭建和打包工具的选择来看: Vue 2.0 中…...
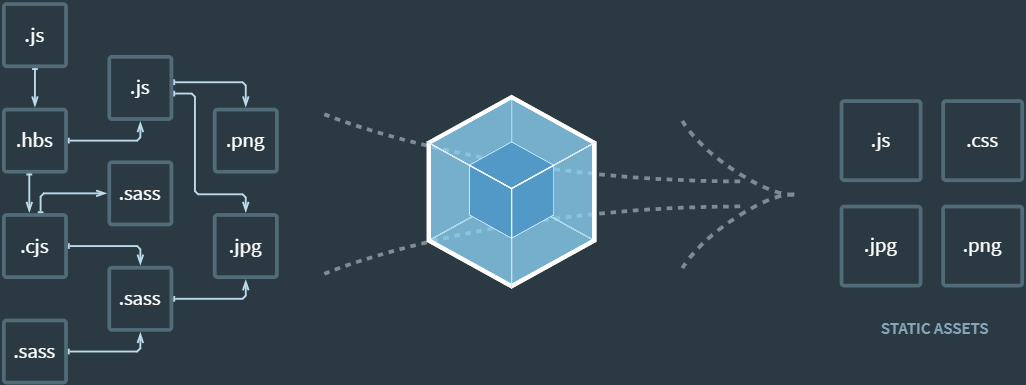
09_Webpack打包工具
1 初识Webpack 1.1 什么是Webpack Webpack打包工具对项目中的复杂文件进行打包处理,可以实现项目的自动化构建,并且给前端开发人员带来了极大的便利。 目前,企业中的绝大多数前端项目是基于Webpack打包工具来进行开发的。 1.2 Webpack的安…...

小程序 | 小程序后端用什么语言开发比较好
目录 ♣️ 引言 选择合适的后端语言 推荐使用Node.js Node.js 的优点 其他备选语言 ♣️ 小结 ♣️ 引言 小程序的兴起已经成为了当今移动互联网时代的热点之一,而小程序后端的好坏直接影响着小程序的使用体验,因此,选择一种好的语言来…...
Websocket升级版
之前写过一个关于websocket的博客,是看书时候做的一个demo。但是纸上得来终觉浅,这次实战后实打实的踩了不少坑,写个博客记录总结。 1.安装postman websocket接口调试,需要8.5以及以上版本的postman 先把以前的卸载,…...
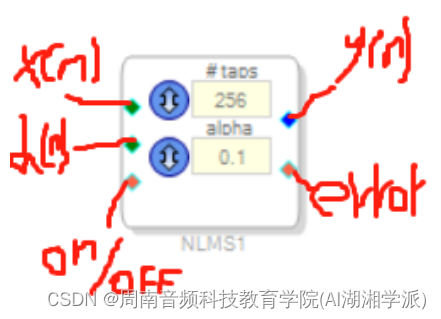
基于音频SOC开发板的主动降噪ANC算法源码实现
基于音频SOC开发板的主动降噪ANC算法源码实现 是否需要申请加入数字音频系统研究开发交流答疑群(课题组)?可加我微信hezkz17, 本群提供音频技术答疑服务,+群附加赠送降噪开发资料,...
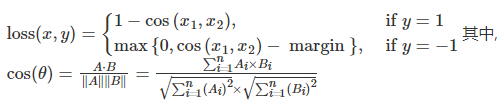
【Pytorch】深度学习之损失函数
文章目录 二分类交叉熵损失函数交叉熵损失函数L1损失函数MSE损失函数平滑L1(Smooth L1)损失函数目标泊松分布的负对数似然损失KL散度MarginRankingLoss多标签边界损失函数二分类损失函数多分类的折页损失三元组损失HingEmbeddingLoss余弦相似度CTC损失函数参考资料 学习目标&am…...

3.4 构造方法
思维导图: 3.4.1 定义构造方法 ### Java中的构造方法 #### **定义与目的** 构造方法,也称为构造器,是一个特殊的成员方法,用于在实例化对象时为对象赋值或执行初始化操作。其主要目的是确保对象在被创建时具有有效和合适的初始状…...

代码随想录
前言 代码随想录算法训练营day43 一、Leetcode 1049. 最后一块石头的重量 II 1.题目 有一堆石头,用整数数组 stones 表示。其中 stones[i] 表示第 i 块石头的重量。 每一回合,从中选出任意两块石头,然后将它们一起粉碎。假设石头的重量分…...
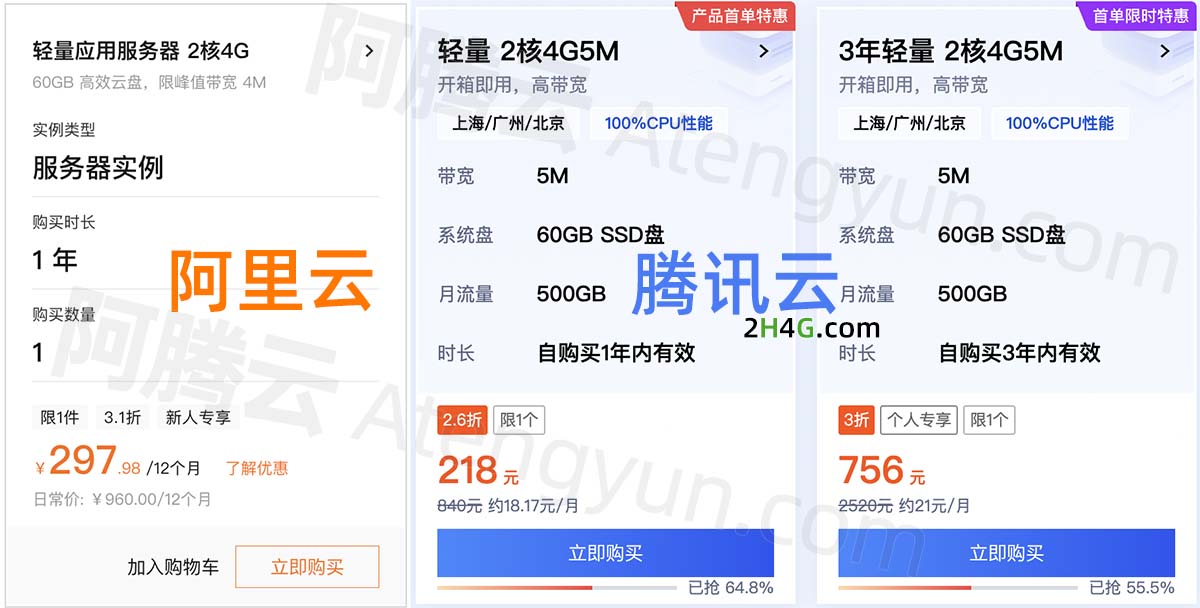
2核4G游戏服务器推荐(阿里云/腾讯云/华为云)
2核4G游戏服务器推荐,首选腾讯云2核4G5M带宽轻量应用服务器218元一年、阿里云2核4G4M带宽轻量应用服务器297元一年,华为云2核2G3M云耀L服务器95元一年,阿腾云来详细说下2核4G游戏服务器推荐配置大全: 目录 2核4G游戏服务器推荐 …...
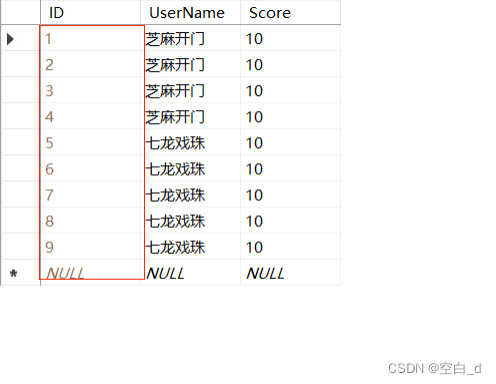
SQL标识列实现自动编号的步骤和技巧以及优势
目录 前言: 过程: 1.步骤: 2.标识种子和表示增量: 效果展示: 优势: 总结: 前言: 在.NET中的例子里面遇到这么一个问题,不能将NULL插入列‘ID’,表Login.dbo.Scores’;列不允许有NULL值。INSERT失败。这个问题很明显,我在SQL数据库中…...
【Debian】报错:su: Authentication failure
项目场景: 今天我重新刷了一个debian系统。 系统版本: # 查看系统版本 lsb_release -a 我的系统版本: No LSB modules are available. Distributor ID:Debian Description: Debian GNU/Linux 12 (bookwormÿ…...

我测试用的mark down教程
Markdown 教程 欢迎使用 Markdown 你好,Markdown是一种类似 Word 的排版工具,你需要仔细阅读这篇文章,了解一下 Markdown 基础知识。 Markdown 功能和列表演示 Markdown 有以下功能,帮助你用它写博客: 数学公式代码高亮导航功能等等Markdown 的优点: 间接高效大厂支持…...
网络编程基础知识总结——IP,端口,协议
目录 1. 什么是网络编程? 2. 网络编程的三要素 3. IP 3.1 IP地址的概念 3.2 IP地址的分类 3.3 IPv4解析 3.4 Ipv6解析 4. IPv4 的使用细节 5. 特殊IP地址 4. 端口号 5. 协议 5.1 UDP协议 5.2 TCP协议 1. 什么是网络编程? 总的来说就是一句…...

【LeetCode力扣】297. 二叉树的序列化与反序列化
目录 1、题目介绍 2、解题思路 2.1、详细过程图解 2.2、代码描述 2.3、完整代码 1、题目介绍 原题链接:297. 二叉树的序列化与反序列化 - 力扣(LeetCode) 示例 1: 输入:root [1,2,3,null,null,4,5] 输出&#…...

Linux寄存器+Linux2.6内核进程调度队列+命令行参数+环境变量
目录 一、寄存器 二、Linux2.6内核进程调度队列 (一)优先级 (二)活动队列 (三)过期队列 (四)active指针和expired指针 三、命令行参数 (一)举例一 &…...
获取C(n,k)组合数列表的QT实现)
组合数(2)获取C(n,k)组合数列表的QT实现
1)工程文件 QT coreCONFIG c17 cmdline# You can make your code fail to compile if it uses deprecated APIs. # In order to do so, uncomment the following line. #DEFINES QT_DISABLE_DEPRECATED_BEFORE0x060000 # disables all the APIs deprecated before Qt 6.…...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

《基于Apache Flink的流处理》笔记
思维导图 1-3 章 4-7章 8-11 章 参考资料 源码: https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...

ArcGIS Pro制作水平横向图例+多级标注
今天介绍下载ArcGIS Pro中如何设置水平横向图例。 之前我们介绍了ArcGIS的横向图例制作:ArcGIS横向、多列图例、顺序重排、符号居中、批量更改图例符号等等(ArcGIS出图图例8大技巧),那这次我们看看ArcGIS Pro如何更加快捷的操作。…...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...

为什么要创建 Vue 实例
核心原因:Vue 需要一个「控制中心」来驱动整个应用 你可以把 Vue 实例想象成你应用的**「大脑」或「引擎」。它负责协调模板、数据、逻辑和行为,将它们变成一个活的、可交互的应用**。没有这个实例,你的代码只是一堆静态的 HTML、JavaScript 变量和函数,无法「活」起来。 …...

深入理解Optional:处理空指针异常
1. 使用Optional处理可能为空的集合 在Java开发中,集合判空是一个常见但容易出错的场景。传统方式虽然可行,但存在一些潜在问题: // 传统判空方式 if (!CollectionUtils.isEmpty(userInfoList)) {for (UserInfo userInfo : userInfoList) {…...

wpf在image控件上快速显示内存图像
wpf在image控件上快速显示内存图像https://www.cnblogs.com/haodafeng/p/10431387.html 如果你在寻找能够快速在image控件刷新大图像(比如分辨率3000*3000的图像)的办法,尤其是想把内存中的裸数据(只有图像的数据,不包…...

【C++】纯虚函数类外可以写实现吗?
1. 答案 先说答案,可以。 2.代码测试 .h头文件 #include <iostream> #include <string>// 抽象基类 class AbstractBase { public:AbstractBase() default;virtual ~AbstractBase() default; // 默认析构函数public:virtual int PureVirtualFunct…...
