代码随想录
前言
代码随想录算法训练营day43
一、Leetcode 1049. 最后一块石头的重量 II
1.题目
有一堆石头,用整数数组 stones 表示。其中 stones[i] 表示第 i 块石头的重量。
每一回合,从中选出任意两块石头,然后将它们一起粉碎。假设石头的重量分别为 x 和 y,且 x <= y。那么粉碎的可能结果如下:
ini
复制代码
如果 x == y,那么两块石头都会被完全粉碎; 如果 x != y,那么重量为 x 的石头将会完全粉碎,而重量为 y 的石头新重量为 y-x。
最后,最多只会剩下一块 石头。返回此石头 最小的可能重量 。如果没有石头剩下,就返回 0。
示例 1:
输入:stones = [2,7,4,1,8,1] 输出:1 解释: 组合 2 和 4,得到 2,所以数组转化为 [2,7,1,8,1], 组合 7 和 8,得到 1,所以数组转化为 [2,1,1,1], 组合 2 和 1,得到 1,所以数组转化为 [1,1,1], 组合 1 和 1,得到 0,所以数组转化为 [1],这就是最优值。
示例 2:
输入:stones = [31,26,33,21,40] 输出:5
提示:
css
复制代码
1 <= stones.length <= 30 1 <= stones[i] <= 100
来源:力扣(LeetCode) 链接:leetcode.cn/problems/la…
2.解题思路
方法一:动态规划
记石头的总重量为 sumsum,ki=−1ki=−1 的石头的重量之和为 negneg,则其余 ki=1ki=1 的石头的重量之和为 sum−negsum−neg。则有
∑i=0n−1ki⋅stonesi=(sum−neg)−neg=sum−2⋅negi=0∑n−1ki⋅stonesi=(sum−neg)−neg=sum−2⋅neg
要使最后一块石头的重量尽可能地小,negneg 需要在不超过 ⌊sum/2⌋⌊sum/2⌋ 的前提下尽可能地大。因此本问题可以看作是背包容量为 ⌊sum/2⌋⌊sum/2⌋,物品重量和价值均为 stonesistonesi 的 0-1 背包问题。
对于该问题,定义二维布尔数组 dpdp,其中 dp[i+1][j]dp[i+1][j] 表示前 ii 个石头能否凑出重量 jj。特别地,dp[0][]dp[0][] 为不选任何石头的状态,因此除了 dp[0][0]dp[0][0] 为真,其余 dp[0][j]dp[0][j] 全为假。
对于第 ii 个石头,考虑凑出重量 jj:
css
复制代码
若 j<stones[i]j<stones[i],则不能选第 ii 个石头,此时有 dp[i+1][j]=dp[i][j]dp[i+1][j]=dp[i][j]; 若 j≥stones[i]j≥stones[i],存在选或不选两种决策,不选时有 dp[i+1][j]=dp[i][j]dp[i+1][j]=dp[i][j],选时需要考虑能否凑出重量 j−stones[i]j−stones[i],即 dp[i+1][j]=dp[i][j−stones[i]]dp[i+1][j]=dp[i][j−stones[i]]。若二者均为假则 dp[i+1][j]dp[i+1][j] 为假,否则 dp[i+1][j]dp[i+1][j] 为真。
因此状态转移方程如下:
dp[i+1][j]={dp[i][j],j<stones[i]dp[i][j]∨dp[i][j−stones[i]],j≥stones[i]dp[i+1][j]={dp[i][j],dp[i][j]∨dp[i][j−stones[i]],j<stones[i]j≥stones[i]
其中 ∨∨ 表示逻辑或运算。求出 dp[n][]dp[n][] 后,所有为真的 dp[n][j]dp[n][j] 中,最大的 jj 即为 negneg 能取到的最大值。代入 sum−2⋅negsum−2⋅neg 中即得到最后一块石头的最小重量。
3.代码实现
java
复制代码
class Solution { public int lastStoneWeightII(int[] stones) { int sum = 0; for (int weight : stones) { sum += weight; } int n = stones.length, m = sum / 2; boolean[][] dp = new boolean[n + 1][m + 1]; dp[0][0] = true; for (int i = 0; i < n; ++i) { for (int j = 0; j <= m; ++j) { if (j < stones[i]) { dp[i + 1][j] = dp[i][j]; } else { dp[i + 1][j] = dp[i][j] || dp[i][j - stones[i]]; } } } for (int j = m;; --j) { if (dp[n][j]) { return sum - 2 * j; } } } }
二、Leetcode 494. 目标和
1.题目
给你一个整数数组 nums 和一个整数 target 。
向数组中的每个整数前添加 '+' 或 '-' ,然后串联起所有整数,可以构造一个 表达式 :
ini
复制代码
例如,nums = [2, 1] ,可以在 2 之前添加 '+' ,在 1 之前添加 '-' ,然后串联起来得到表达式 "+2-1" 。
返回可以通过上述方法构造的、运算结果等于 target 的不同 表达式 的数目。
示例 1:
输入:nums = [1,1,1,1,1], target = 3 输出:5 解释:一共有 5 种方法让最终目标和为 3 。 -1 + 1 + 1 + 1 + 1 = 3 +1 - 1 + 1 + 1 + 1 = 3 +1 + 1 - 1 + 1 + 1 = 3 +1 + 1 + 1 - 1 + 1 = 3 +1 + 1 + 1 + 1 - 1 = 3
示例 2:
输入:nums = [1], target = 1 输出:1
提示:
scss
复制代码
1 <= nums.length <= 20 0 <= nums[i] <= 1000 0 <= sum(nums[i]) <= 1000 -1000 <= target <= 1000
来源:力扣(LeetCode) 链接:leetcode.cn/problems/ta…
2.解题思路
方法一:回溯
数组 numsnums 的每个元素都可以添加符号 ++ 或 --,因此每个元素有 22 种添加符号的方法,nn 个数共有 2n2n 种添加符号的方法,对应 2n2n 种不同的表达式。当 nn 个元素都添加符号之后,即得到一种表达式,如果表达式的结果等于目标数 targettarget,则该表达式即为符合要求的表达式。
可以使用回溯的方法遍历所有的表达式,回溯过程中维护一个计数器 countcount,当遇到一种表达式的结果等于目标数 targettarget 时,将 countcount 的值加 11。遍历完所有的表达式之后,即可得到结果等于目标数 targettarget 的表达式的数目。
3.代码实现
java
复制代码
class Solution { int count = 0; public int findTargetSumWays(int[] nums, int target) { backtrack(nums, target, 0, 0); return count; } public void backtrack(int[] nums, int target, int index, int sum) { if (index == nums.length) { if (sum == target) { count++; } } else { backtrack(nums, target, index + 1, sum + nums[index]); backtrack(nums, target, index + 1, sum - nums[index]); } } }
三、Leetcode 474.一和零
1.题目
给你一个二进制字符串数组 strs 和两个整数 m 和 n 。
请你找出并返回 strs 的最大子集的长度,该子集中 最多 有 m 个 0 和 n 个 1 。
如果 x 的所有元素也是 y 的元素,集合 x 是集合 y 的 子集 。
示例 1:
输入:strs = ["10", "0001", "111001", "1", "0"], m = 5, n = 3 输出:4 解释:最多有 5 个 0 和 3 个 1 的最大子集是 {"10","0001","1","0"} ,因此答案是 4 。 其他满足题意但较小的子集包括 {"0001","1"} 和 {"10","1","0"} 。{"111001"} 不满足题意,因为它含 4 个 1 ,大于 n 的值 3 。
示例 2:
输入:strs = ["10", "0", "1"], m = 1, n = 1 输出:2 解释:最大的子集是 {"0", "1"} ,所以答案是 2 。
提示:
matlab
复制代码
1 <= strs.length <= 600 1 <= strs[i].length <= 100 strs[i] 仅由 '0' 和 '1' 组成 1 <= m, n <= 100
来源:力扣(LeetCode) 链接:leetcode.cn/problems/on…
2.解题思路
方法一:动态规划
这道题和经典的背包问题非常相似,但是和经典的背包问题只有一种容量不同,这道题有两种容量,即选取的字符串子集中的 00 和 11 的数量上限。
经典的背包问题可以使用二维动态规划求解,两个维度分别是物品和容量。这道题有两种容量,因此需要使用三维动态规划求解,三个维度分别是字符串、00 的容量和 11 的容量。
定义三维数组 dpdp,其中 dp[i][j][k]dp[i][j][k] 表示在前 ii 个字符串中,使用 jj 个 00 和 kk 个 11 的情况下最多可以得到的字符串数量。假设数组 strstr 的长度为 ll,则最终答案为 dp[l][m][n]dp[l][m][n]。
当没有任何字符串可以使用时,可以得到的字符串数量只能是 00,因此动态规划的边界条件是:当 i=0i=0 时,对任意 0≤j≤m0≤j≤m 和 0≤k≤n0≤k≤n,都有 dp[i][j][k]=0dp[i][j][k]=0。
当 1≤i≤l1≤i≤l 时,对于 strsstrs 中的第 ii 个字符串(计数从 11 开始),首先遍历该字符串得到其中的 00 和 11 的数量,分别记为 zeroszeros 和 onesones,然后对于 0≤j≤m0≤j≤m 和 0≤k≤n0≤k≤n,计算 dp[i][j][k]dp[i][j][k] 的值。
当 00 和 11 的容量分别是 jj 和 kk 时,考虑以下两种情况:
css
复制代码
如果 j<zerosj<zeros 或 k<onesk<ones,则不能选第 ii 个字符串,此时有 dp[i][j][k]=dp[i−1][j][k]dp[i][j][k]=dp[i−1][j][k]; 如果 j≥zerosj≥zeros 且 k≥onesk≥ones,则如果不选第 ii 个字符串,有 dp[i][j][k]=dp[i−1][j][k]dp[i][j][k]=dp[i−1][j][k],如果选第 ii 个字符串,有 dp[i][j][k]=dp[i−1][j−zeros][k−ones]+1dp[i][j][k]=dp[i−1][j−zeros][k−ones]+1,dp[i][j][k]dp[i][j][k] 的值应取上面两项中的最大值。
因此状态转移方程如下:
dp[i][j][k]={dp[i−1][j][k],j<zeros ∣ k<onesmax(dp[i−1][j][k],dp[i−1][j−zeros][k−ones]+1),j≥zeros & k≥onesdp[i][j][k]={dp[i−1][j][k],max(dp[i−1][j][k],dp[i−1][j−zeros][k−ones]+1),j<zeros ∣ k<onesj≥zeros & k≥ones
最终得到 dp[l][m][n]dp[l][m][n] 的值即为答案。
由此可以得到空间复杂度为 O(lmn)O(lmn) 的实现。
3.代码实现
java
复制代码
class Solution { public int findMaxForm(String[] strs, int m, int n) { int length = strs.length; int[][][] dp = new int[length + 1][m + 1][n + 1]; for (int i = 1; i <= length; i++) { int[] zerosOnes = getZerosOnes(strs[i - 1]); int zeros = zerosOnes[0], ones = zerosOnes[1]; for (int j = 0; j <= m; j++) { for (int k = 0; k <= n; k++) { dp[i][j][k] = dp[i - 1][j][k]; if (j >= zeros && k >= ones) { dp[i][j][k] = Math.max(dp[i][j][k], dp[i - 1][j - zeros][k - ones] + 1); } } } } return dp[length][m][n]; } public int[] getZerosOnes(String str) { int[] zerosOnes = new int[2]; int length = str.length(); for (int i = 0; i < length; i++) { zerosOnes[str.charAt(i) - '0']++; } return zerosOnes; } }
相关文章:

代码随想录
前言 代码随想录算法训练营day43 一、Leetcode 1049. 最后一块石头的重量 II 1.题目 有一堆石头,用整数数组 stones 表示。其中 stones[i] 表示第 i 块石头的重量。 每一回合,从中选出任意两块石头,然后将它们一起粉碎。假设石头的重量分…...
2核4G游戏服务器推荐(阿里云/腾讯云/华为云)
2核4G游戏服务器推荐,首选腾讯云2核4G5M带宽轻量应用服务器218元一年、阿里云2核4G4M带宽轻量应用服务器297元一年,华为云2核2G3M云耀L服务器95元一年,阿腾云来详细说下2核4G游戏服务器推荐配置大全: 目录 2核4G游戏服务器推荐 …...
SQL标识列实现自动编号的步骤和技巧以及优势
目录 前言: 过程: 1.步骤: 2.标识种子和表示增量: 效果展示: 优势: 总结: 前言: 在.NET中的例子里面遇到这么一个问题,不能将NULL插入列‘ID’,表Login.dbo.Scores’;列不允许有NULL值。INSERT失败。这个问题很明显,我在SQL数据库中…...
【Debian】报错:su: Authentication failure
项目场景: 今天我重新刷了一个debian系统。 系统版本: # 查看系统版本 lsb_release -a 我的系统版本: No LSB modules are available. Distributor ID:Debian Description: Debian GNU/Linux 12 (bookwormÿ…...

我测试用的mark down教程
Markdown 教程 欢迎使用 Markdown 你好,Markdown是一种类似 Word 的排版工具,你需要仔细阅读这篇文章,了解一下 Markdown 基础知识。 Markdown 功能和列表演示 Markdown 有以下功能,帮助你用它写博客: 数学公式代码高亮导航功能等等Markdown 的优点: 间接高效大厂支持…...
网络编程基础知识总结——IP,端口,协议
目录 1. 什么是网络编程? 2. 网络编程的三要素 3. IP 3.1 IP地址的概念 3.2 IP地址的分类 3.3 IPv4解析 3.4 Ipv6解析 4. IPv4 的使用细节 5. 特殊IP地址 4. 端口号 5. 协议 5.1 UDP协议 5.2 TCP协议 1. 什么是网络编程? 总的来说就是一句…...

【LeetCode力扣】297. 二叉树的序列化与反序列化
目录 1、题目介绍 2、解题思路 2.1、详细过程图解 2.2、代码描述 2.3、完整代码 1、题目介绍 原题链接:297. 二叉树的序列化与反序列化 - 力扣(LeetCode) 示例 1: 输入:root [1,2,3,null,null,4,5] 输出&#…...

Linux寄存器+Linux2.6内核进程调度队列+命令行参数+环境变量
目录 一、寄存器 二、Linux2.6内核进程调度队列 (一)优先级 (二)活动队列 (三)过期队列 (四)active指针和expired指针 三、命令行参数 (一)举例一 &…...
获取C(n,k)组合数列表的QT实现)
组合数(2)获取C(n,k)组合数列表的QT实现
1)工程文件 QT coreCONFIG c17 cmdline# You can make your code fail to compile if it uses deprecated APIs. # In order to do so, uncomment the following line. #DEFINES QT_DISABLE_DEPRECATED_BEFORE0x060000 # disables all the APIs deprecated before Qt 6.…...

SparkCore编程RDD
RDD概述 中文名为弹性分布式数据集,是数据处理基本单位。代表一个弹性的,不可变,可分区,里面的数据可并行计算的集合。 RDD和Hadoop MR 的区别: RDD是先明确数据处理流程,数据在行动算子执行前实际上并未…...

VBA技术资料MF69:添加和删除工作表中的分页符
我给VBA的定义:VBA是个人小型自动化处理的有效工具。利用好了,可以大大提高自己的工作效率,而且可以提高数据的准确度。我的教程一共九套,分为初级、中级、高级三大部分。是对VBA的系统讲解,从简单的入门,到…...

数字技术助力智慧公厕,让公厕变身为全新创新应用
在如今数字化的时代,数字技术的集成应用已经渗透到了生活的方方面面。其中一个令人瞩目的领域就是智慧公厕。以前只是简单的厕所,如今借助数字技术的力量,智慧公厕变得功能强大、智能高效。接下来,我们将以智慧公厕源头领航厂家广…...
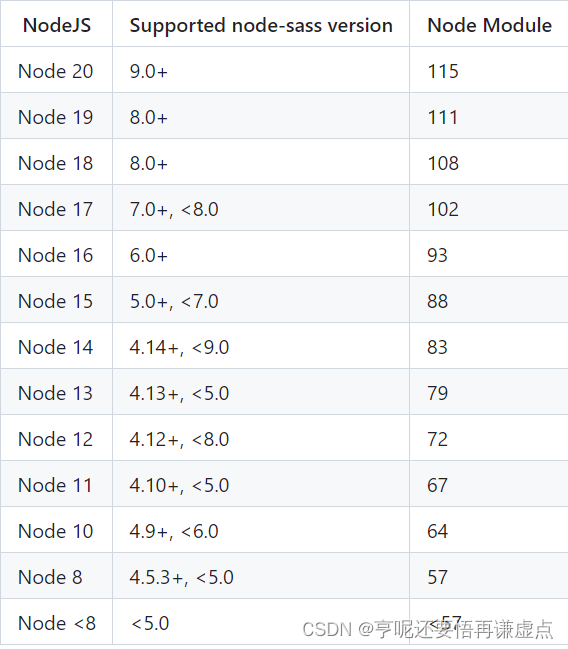
electron 升级 v22 遇到问题
Electron 漏洞 https://mp.weixin.qq.com/s/5LpSJb_5uV8EIDOl3fz9Tw 由于 23以上不在支持win 7 8 8.1 所以我选择安装 v22.3.24 electron 22.3.24 node-sass 6.0.1 sass-loader 10.4.1 对应的版本 npm i node-sass6.0.1 --sass_binary_sitehttps://npm.taobao.org/mirrors…...

跟我学c++中级篇——Pimpl
一、前向声明 前向声明或者前置声明(forward declaration),这个在c中用得还是比较多的。一般的框架或者库中,经常可以看到在一个类的前面声明了一个类,类似下面这样: class useclass; class mycall{...useclass *us; };前向声明…...
[补题记录] Atcoder Beginner Contest 295(E)
URL:https://atcoder.jp/contests/abc295 目录 E Problem/题意 Thought/思路 Code/代码 E Problem/题意 给定长度为 N 的数组 A。进行如下操作: 若 Ai 0,将 Ai 等概率地变为 1 ~ M 中的任意一个数;对 A 排序; …...
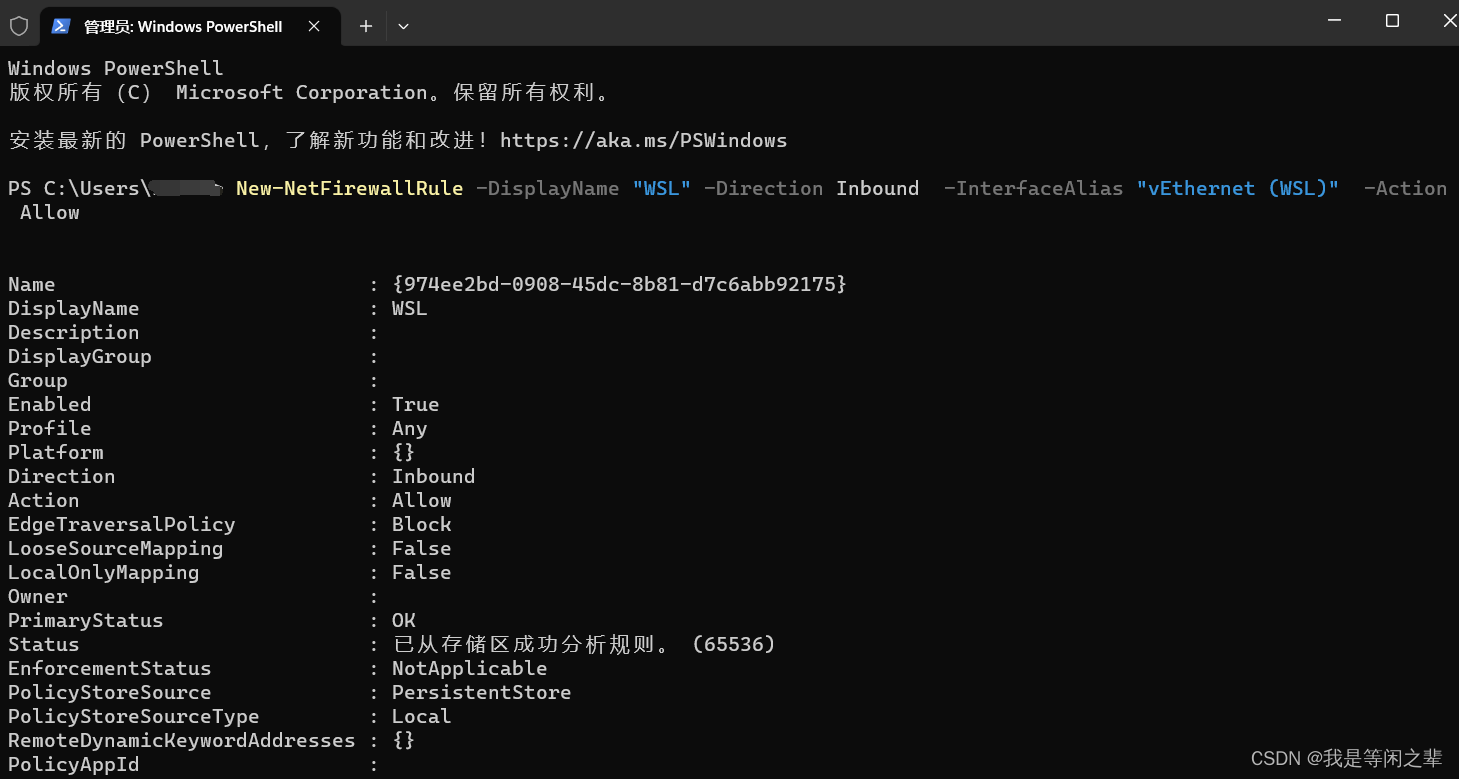
解决git在window11操作很慢,占用很大cpu的问题
【git在window11操作很慢,占用很大cpu,最后也执行失败】 在谷歌输入:git very slow in window 11。通过下面链接终于找到了解决方案: https://www.reddit.com/r/vscode/comments/sulebx/slow_git_in_wsl_after_updating_to_window…...
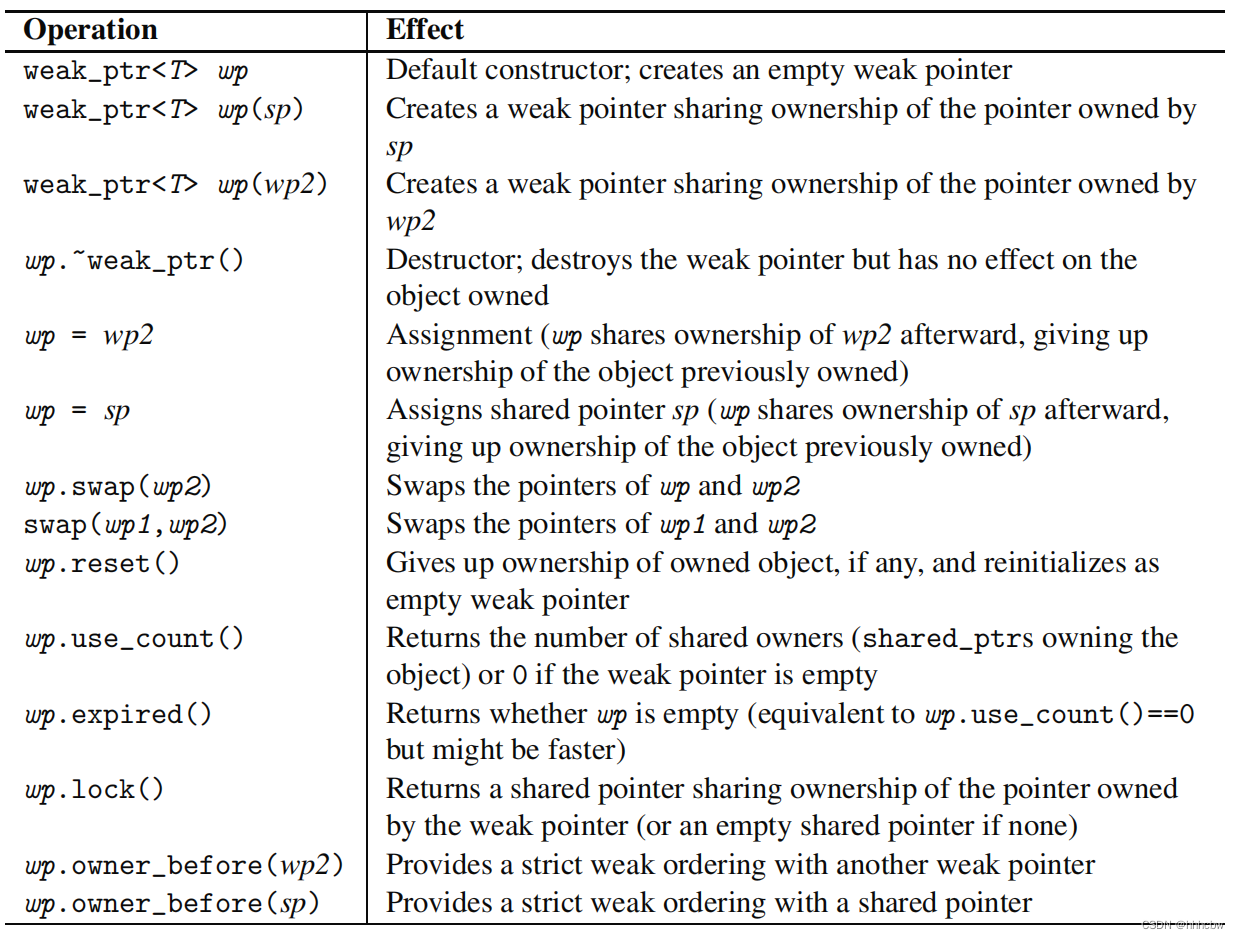
C++智能指针(二)——weak_ptr初探
文章目录 1. shared_ptr 存在的问题2. 使用weak_ptr2.1 初始化 weak_ptr2.2 访问数据 3. 附录4. 参考文献 1. shared_ptr 存在的问题 与 shared_ptr 的引入要解决普通指针存在的一些问题一样,weak_ptr 的引入,也是因为 shared_ptr 本身在某些情况下&…...
)
540 - Team Queue (UVA)
题目链接如下: Online Judge 对比刘汝佳的代码,我没有用queue来排整个队伍,因为那样的话遍历整个队伍太麻烦,vector比较方便。但vector删除元素比较耗时,所以就不删了,仅仅用pivot来指代目前队伍的开始。…...
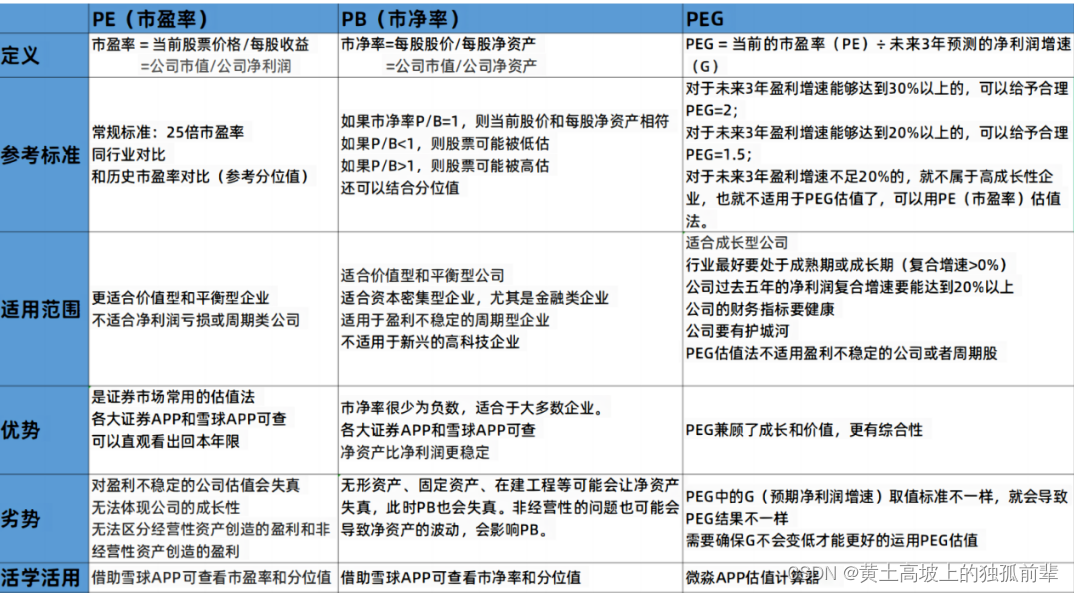
投资组合之如何估值
文章目录 如何估值一、PE估值法1、PE估值法的定义2、参考标准(1)常规标准:25倍合理市盈率。(2)同行业对比。(3)跟历史市盈率相比。 3、PE估值法的适用范围4、PE估值法的优势5、PE估值法的劣势&a…...
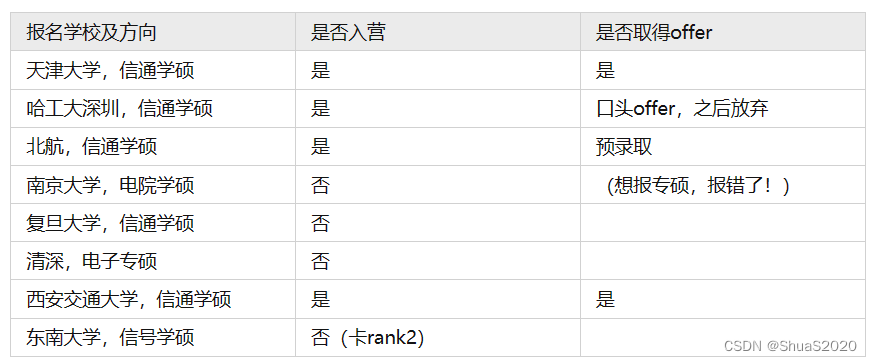
2024届通信工程保研经验分享(预推免入营即offer)
2024届通信工程保研经验分享(预推免入营即offer) BackGround夏令营情况:预推免情况: BackGround 本科院校:末九 专业:通信工程 rank:3/123(预推免绩点排名)࿰…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

技术栈RabbitMq的介绍和使用
目录 1. 什么是消息队列?2. 消息队列的优点3. RabbitMQ 消息队列概述4. RabbitMQ 安装5. Exchange 四种类型5.1 direct 精准匹配5.2 fanout 广播5.3 topic 正则匹配 6. RabbitMQ 队列模式6.1 简单队列模式6.2 工作队列模式6.3 发布/订阅模式6.4 路由模式6.5 主题模式…...

学习一下用鸿蒙DevEco Studio HarmonyOS5实现百度地图
在鸿蒙(HarmonyOS5)中集成百度地图,可以通过以下步骤和技术方案实现。结合鸿蒙的分布式能力和百度地图的API,可以构建跨设备的定位、导航和地图展示功能。 1. 鸿蒙环境准备 开发工具:下载安装 De…...

aardio 自动识别验证码输入
技术尝试 上周在发学习日志时有网友提议“在网页上识别验证码”,于是尝试整合图像识别与网页自动化技术,完成了这套模拟登录流程。核心思路是:截图验证码→OCR识别→自动填充表单→提交并验证结果。 代码在这里 import soImage; import we…...

【Ftrace 专栏】Ftrace 参考博文
ftrace、perf、bcc、bpftrace、ply、simple_perf的使用Ftrace 基本用法Linux 利用 ftrace 分析内核调用如何利用ftrace精确跟踪特定进程调度信息使用 ftrace 进行追踪延迟Linux-培训笔记-ftracehttps://www.kernel.org/doc/html/v4.18/trace/events.htmlhttps://blog.csdn.net/…...

鸿蒙Navigation路由导航-基本使用介绍
1. Navigation介绍 Navigation组件是路由导航的根视图容器,一般作为Page页面的根容器使用,其内部默认包含了标题栏、内容区和工具栏,其中内容区默认首页显示导航内容(Navigation的子组件)或非首页显示(Nav…...
