组合数(2)获取C(n,k)组合数列表的QT实现
1)工程文件
QT = coreCONFIG += c++17 cmdline# You can make your code fail to compile if it uses deprecated APIs.
# In order to do so, uncomment the following line.
#DEFINES += QT_DISABLE_DEPRECATED_BEFORE=0x060000 # disables all the APIs deprecated before Qt 6.0.0SOURCES += \main.cpp# Default rules for deployment.
qnx: target.path = /tmp/$${TARGET}/bin
else: unix:!android: target.path = /opt/$${TARGET}/bin
!isEmpty(target.path): INSTALLS += target
2)主程序
#include <QCoreApplication>
#include <vector>
#include <iostream>using namespace std;
const int N = 10;
const int K = 5;vector<vector<int>> getCombinationvector(int nums[],int ncount)
{vector<vector<int>> retvv = vector<vector<int>>();retvv.push_back(vector<int>());for (int n=0; n<ncount; n++) {int size = retvv.size();for (int i = 0; i < size; i++) {vector<int> newSub = vector<int>(retvv[i]);newSub.push_back(n);retvv.push_back(newSub);}}return retvv;
}void showCombinationvector( vector<vector<int>> va )
{std::cout << "C(" << N <<"," << K <<") = " << va.size() << "\n";std::cout << "[ \n";for (int var = 0; var < va.size(); ++var) {std::cout << " [ ";for(int j=0; j< va[var].size();j++){std::cout << va[var][j] << " ";}std::cout << "]\n";}std::cout << "]\n";
}vector<vector<int>> getCombineNK(int n, int k) {vector<int> nums = vector<int>();for(int i = 1; i < k + 1; ++i)nums.push_back(i);nums.push_back(n + 1);vector<vector<int>> retvv = vector<vector<int>>();int j = 0;while (j < k) {retvv.push_back(vector<int>(nums.begin(), nums.begin() + k));j = 0;while ((j < k) && (nums[j + 1] == nums[j] + 1)){nums[j] = j + 1;j++;}nums[j] ++ ;}return retvv;
}int main(int argc, char *argv[])
{QCoreApplication a(argc, argv);int test[] = {1,2,3,4,5};//vector<vector<int>> va = getCombinationvector(test, 5);vector<vector<int>> va = getCombineNK(10, 5);showCombinationvector(va);return a.exec();
}
3)运行结果
C(10,5) = 252
[
[ 1 2 3 4 5 ]
[ 1 2 3 4 6 ]
[ 1 2 3 5 6 ]
[ 1 2 4 5 6 ]
[ 1 3 4 5 6 ]
[ 2 3 4 5 6 ]
[ 1 2 3 4 7 ]
[ 1 2 3 5 7 ]
[ 1 2 4 5 7 ]
[ 1 3 4 5 7 ]
[ 2 3 4 5 7 ]
[ 1 2 3 6 7 ]
[ 1 2 4 6 7 ]
[ 1 3 4 6 7 ]
[ 2 3 4 6 7 ]
[ 1 2 5 6 7 ]
[ 1 3 5 6 7 ]
[ 2 3 5 6 7 ]
[ 1 4 5 6 7 ]
[ 2 4 5 6 7 ]
[ 3 4 5 6 7 ]
[ 1 2 3 4 8 ]
[ 1 2 3 5 8 ]
[ 1 2 4 5 8 ]
[ 1 3 4 5 8 ]
[ 2 3 4 5 8 ]
[ 1 2 3 6 8 ]
[ 1 2 4 6 8 ]
[ 1 3 4 6 8 ]
[ 2 3 4 6 8 ]
[ 1 2 5 6 8 ]
[ 1 3 5 6 8 ]
[ 2 3 5 6 8 ]
[ 1 4 5 6 8 ]
[ 2 45 6 8 ]
[ 3 4 5 6 8 ]
[ 1 2 3 7 8 ]
[ 1 2 4 7 8 ]
[ 1 3 4 7 8 ]
[ 2 3 4 7 8 ]
[ 1 2 5 7 8 ]
[ 1 3 5 7 8 ]
[ 2 3 5 7 8 ]
[ 1 4 5 7 8 ]
[ 2 4 5 7 8 ]
[ 3 4 5 7 8 ]
[ 1 2 6 7 8 ]
[ 1 3 6 7 8 ]
[ 2 3 6 7 8 ]
[ 1 4 6 7 8 ]
[ 2 4 6 7 8 ]
[ 3 4 6 7 8 ]
[ 1 5 6 7 8 ]
[ 2 5 6 7 8 ]
[ 3 5 6 7 8 ]
[ 4 5 6 7 8 ]
[ 1 2 3 4 9 ]
[ 1 2 3 5 9 ]
[ 1 2 4 5 9 ]
[ 1 3 4 5 9 ]
[ 2 3 4 5 9 ]
[ 1 2 3 6 9 ]
[ 1 2 4 6 9 ]
[ 1 3 4 6 9 ]
[ 2 3 4 6 9 ]
[ 1 2 5 6 9 ]
[ 1 3 5 6 9 ]
[ 2 3 5 6 9 ]
[ 1 4 5 6 9 ]
[ 2 4 5 6 9 ]
[ 3 4 5 6 9 ]
[ 1 2 3 7 9 ]
[ 1 2 4 7 9 ]
[ 1 3 4 7 9 ]
[ 2 3 4 7 9 ]
[ 1 2 5 7 9 ]
[ 1 3 5 7 9 ]
[ 2 3 5 7 9 ]
[ 1 4 5 7 9 ]
[ 2 4 5 7 9 ]
[ 3 4 5 7 9 ]
[ 1 2 6 7 9 ]
[ 1 3 6 7 9 ]
[ 2 3 6 7 9 ]
[ 1 4 6 7 9 ]
[ 2 4 6 7 9 ]
[ 3 4 6 7 9 ]
[ 1 5 6 7 9 ]
[ 2 5 6 7 9 ]
[ 3 5 6 7 9 ]
[ 4 5 6 7 9 ]
[ 1 2 3 8 9 ]
[ 1 2 4 8 9 ]
[ 1 3 4 8 9 ]
[ 2 3 4 8 9 ]
[ 1 2 5 8 9 ]
[ 1 3 5 8 9 ]
[ 2 3 5 8 9 ]
[ 1 4 5 8 9 ]
[ 2 45 8 9 ]
[ 3 4 5 8 9 ]
[ 1 2 6 8 9 ]
[ 1 3 6 8 9 ]
[ 2 3 6 8 9 ]
[ 1 4 6 8 9 ]
[ 2 4 6 8 9 ]
[ 3 4 6 8 9 ]
[ 1 5 6 8 9 ]
[ 2 5 6 8 9 ]
[ 3 5 6 8 9 ]
[ 4 5 6 8 9 ]
[ 1 2 7 8 9 ]
[ 1 3 7 8 9 ]
[ 2 3 7 8 9 ]
[ 1 4 7 8 9 ]
[ 2 4 7 8 9 ]
[ 3 4 7 8 9 ]
[ 1 5 7 8 9 ]
[ 2 5 7 8 9 ]
[ 3 5 7 8 9 ]
[ 4 5 7 8 9 ]
[ 1 6 7 8 9 ]
[ 2 6 7 8 9 ]
[ 3 6 7 8 9 ]
[ 4 6 7 8 9 ]
[ 5 6 7 8 9 ]
[ 1 2 3 4 10 ]
[ 1 2 3 5 10 ]
[ 1 2 4 5 10 ]
[ 1 3 4 5 10 ]
[ 2 3 4 5 10 ]
[ 1 2 3 6 10 ]
[ 1 2 4 6 10 ]
[ 1 3 4 6 10 ]
[ 2 3 4 6 10 ]
[ 1 2 5 6 10 ]
[ 1 3 5 6 10 ]
[ 2 3 5 6 10 ]
[ 1 4 5 6 10 ]
[ 2 4 5 6 10 ]
[ 3 4 5 6 10 ]
[ 1 2 3 7 10 ]
[ 1 2 4 7 10 ]
[ 1 3 4 7 10 ]
[ 2 3 4 7 10 ]
[ 1 2 5 7 10 ]
[ 1 3 5 7 10 ]
[ 2 3 5 7 10 ]
[ 1 4 5 7 10 ]
[ 2 4 5 7 10 ]
[ 3 4 5 7 10 ]
[ 1 2 6 7 10 ]
[ 1 3 6 7 10 ]
[ 2 3 6 7 10 ]
[ 1 4 6 7 10 ]
[ 2 4 6 7 10 ]
[ 3 4 6 7 10 ]
[ 1 5 6 7 10 ]
[ 2 5 6 7 10 ]
[ 3 5 6 7 10 ]
[ 4 5 6 7 10 ]
[ 1 2 3 8 10 ]
[ 1 2 4 8 10 ]
[ 1 3 4 8 10 ]
[ 2 3 4 8 10 ]
[ 1 2 5 8 10 ]
[ 1 3 5 8 10 ]
[ 2 3 5 8 10 ]
[ 1 4 5 8 10 ]
[ 2 4 5 8 10 ]
[ 3 4 5 8 10 ]
[ 1 2 6 8 10 ]
[ 1 3 6 8 10 ]
[ 2 3 6 8 10 ]
[ 1 4 6 8 10 ]
[ 2 4 6 8 10 ]
[ 3 4 6 8 10 ]
[ 1 5 6 8 10 ]
[ 2 5 6 8 10 ]
[ 3 5 6 8 10 ]
[ 4 5 6 8 10 ]
[ 1 2 7 8 10 ]
[ 1 3 7 8 10 ]
[ 2 3 7 8 10 ]
[ 1 4 7 8 10 ]
[ 2 4 7 8 10 ]
[ 3 4 7 8 10 ]
[ 1 5 7 8 10 ]
[ 2 5 7 8 10 ]
[ 3 5 7 8 10 ]
[ 4 5 7 8 10 ]
[ 1 6 7 8 10 ]
[ 2 6 7 8 10 ]
[ 3 6 7 8 10 ]
[ 4 6 7 8 10 ]
[ 2 6 8 9 10 ]
[ 3 6 8 9 10 ]
[ 4 6 8 9 10 ]
[ 5 6 8 9 10 ]
[ 1 7 8 9 10 ]
[ 2 7 8 9 10 ]
[ 3 7 8 9 10 ]
[ 4 7 8 9 10 ]
[ 5 7 8 9 10 ]
[ 6 7 8 9 10 ]
]
相关文章:
获取C(n,k)组合数列表的QT实现)
组合数(2)获取C(n,k)组合数列表的QT实现
1)工程文件 QT coreCONFIG c17 cmdline# You can make your code fail to compile if it uses deprecated APIs. # In order to do so, uncomment the following line. #DEFINES QT_DISABLE_DEPRECATED_BEFORE0x060000 # disables all the APIs deprecated before Qt 6.…...

SparkCore编程RDD
RDD概述 中文名为弹性分布式数据集,是数据处理基本单位。代表一个弹性的,不可变,可分区,里面的数据可并行计算的集合。 RDD和Hadoop MR 的区别: RDD是先明确数据处理流程,数据在行动算子执行前实际上并未…...

VBA技术资料MF69:添加和删除工作表中的分页符
我给VBA的定义:VBA是个人小型自动化处理的有效工具。利用好了,可以大大提高自己的工作效率,而且可以提高数据的准确度。我的教程一共九套,分为初级、中级、高级三大部分。是对VBA的系统讲解,从简单的入门,到…...

数字技术助力智慧公厕,让公厕变身为全新创新应用
在如今数字化的时代,数字技术的集成应用已经渗透到了生活的方方面面。其中一个令人瞩目的领域就是智慧公厕。以前只是简单的厕所,如今借助数字技术的力量,智慧公厕变得功能强大、智能高效。接下来,我们将以智慧公厕源头领航厂家广…...
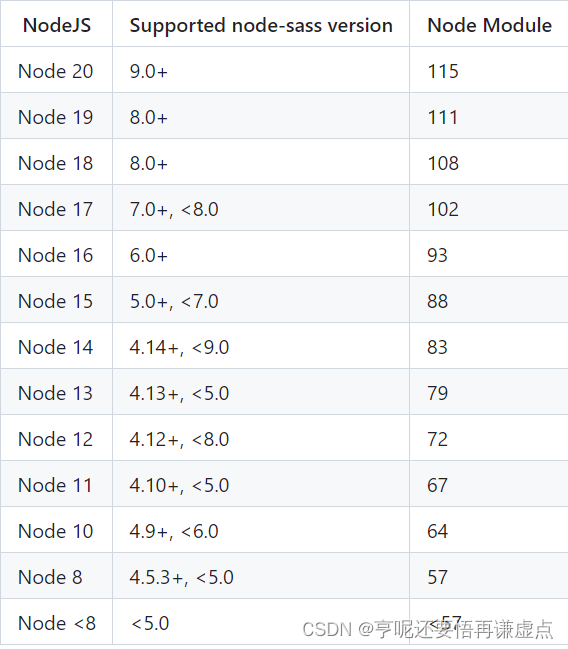
electron 升级 v22 遇到问题
Electron 漏洞 https://mp.weixin.qq.com/s/5LpSJb_5uV8EIDOl3fz9Tw 由于 23以上不在支持win 7 8 8.1 所以我选择安装 v22.3.24 electron 22.3.24 node-sass 6.0.1 sass-loader 10.4.1 对应的版本 npm i node-sass6.0.1 --sass_binary_sitehttps://npm.taobao.org/mirrors…...

跟我学c++中级篇——Pimpl
一、前向声明 前向声明或者前置声明(forward declaration),这个在c中用得还是比较多的。一般的框架或者库中,经常可以看到在一个类的前面声明了一个类,类似下面这样: class useclass; class mycall{...useclass *us; };前向声明…...
[补题记录] Atcoder Beginner Contest 295(E)
URL:https://atcoder.jp/contests/abc295 目录 E Problem/题意 Thought/思路 Code/代码 E Problem/题意 给定长度为 N 的数组 A。进行如下操作: 若 Ai 0,将 Ai 等概率地变为 1 ~ M 中的任意一个数;对 A 排序; …...
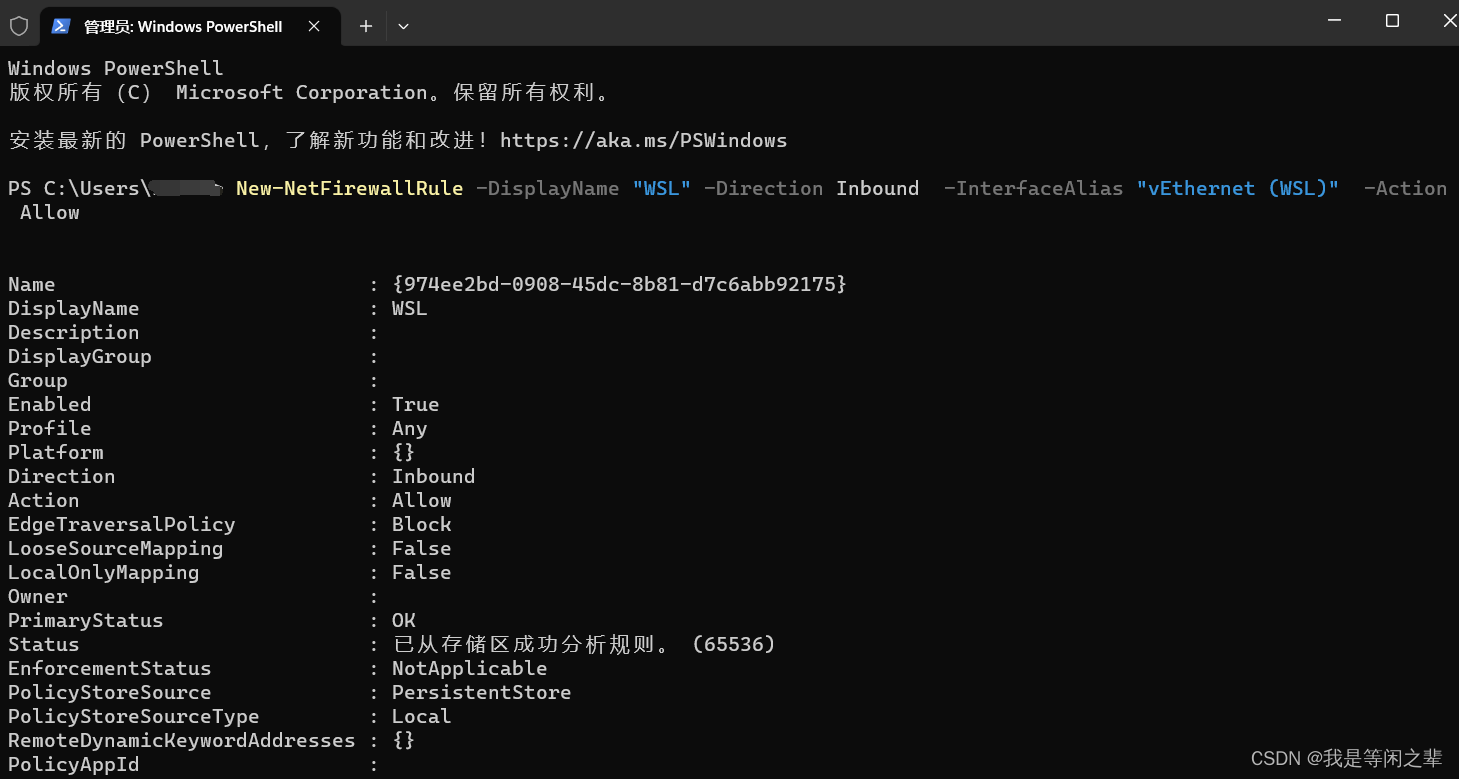
解决git在window11操作很慢,占用很大cpu的问题
【git在window11操作很慢,占用很大cpu,最后也执行失败】 在谷歌输入:git very slow in window 11。通过下面链接终于找到了解决方案: https://www.reddit.com/r/vscode/comments/sulebx/slow_git_in_wsl_after_updating_to_window…...
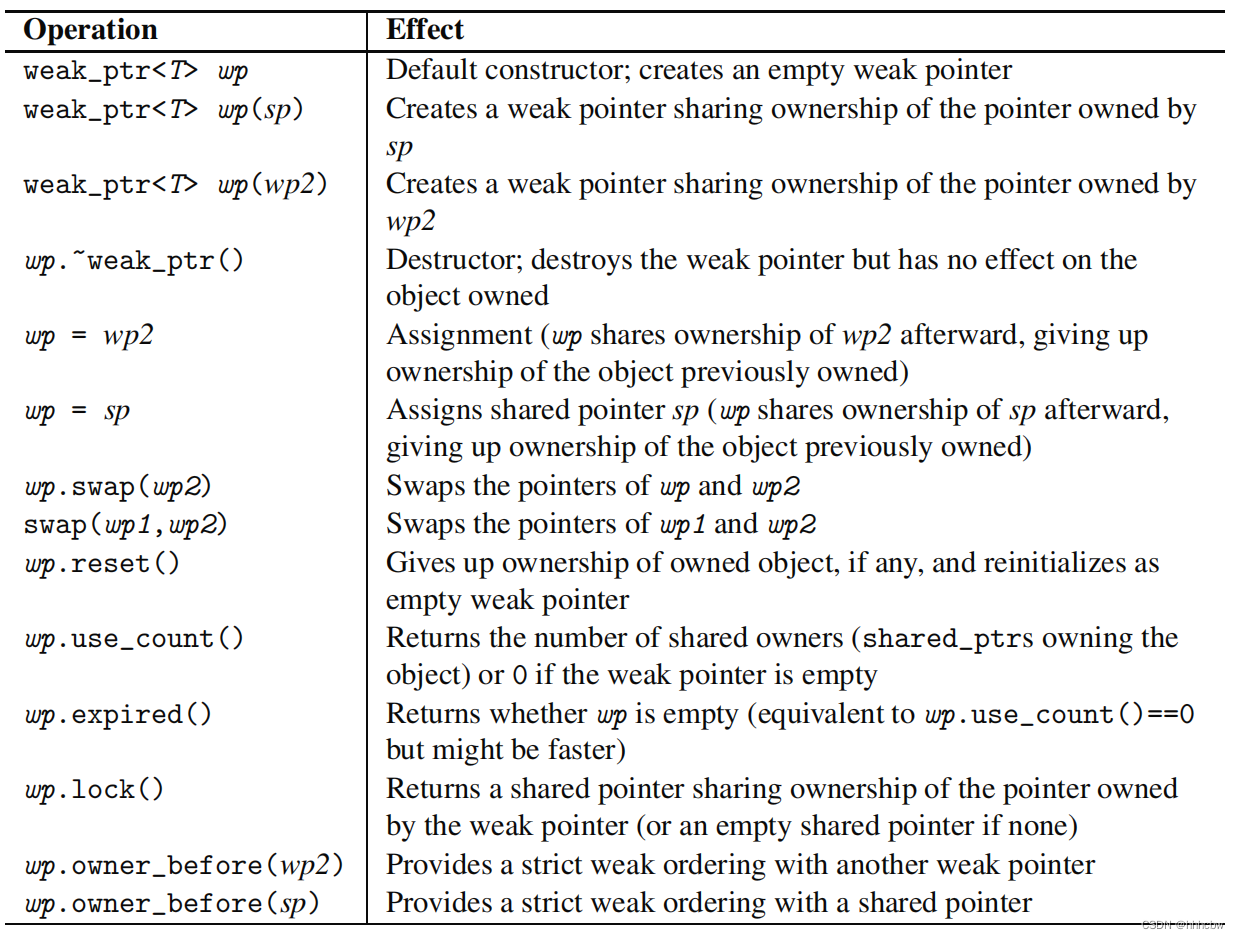
C++智能指针(二)——weak_ptr初探
文章目录 1. shared_ptr 存在的问题2. 使用weak_ptr2.1 初始化 weak_ptr2.2 访问数据 3. 附录4. 参考文献 1. shared_ptr 存在的问题 与 shared_ptr 的引入要解决普通指针存在的一些问题一样,weak_ptr 的引入,也是因为 shared_ptr 本身在某些情况下&…...
)
540 - Team Queue (UVA)
题目链接如下: Online Judge 对比刘汝佳的代码,我没有用queue来排整个队伍,因为那样的话遍历整个队伍太麻烦,vector比较方便。但vector删除元素比较耗时,所以就不删了,仅仅用pivot来指代目前队伍的开始。…...
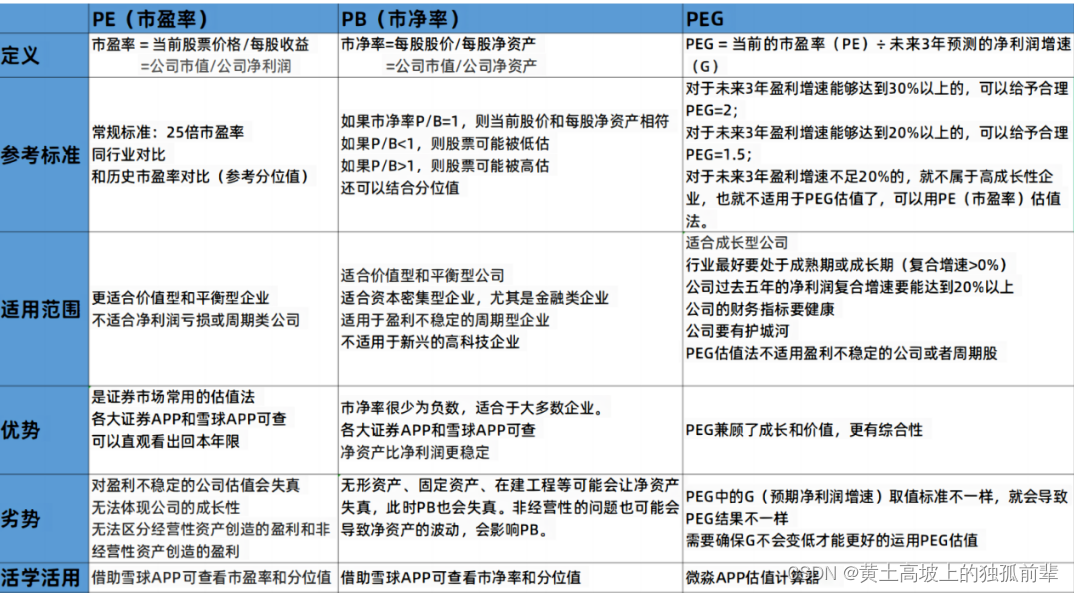
投资组合之如何估值
文章目录 如何估值一、PE估值法1、PE估值法的定义2、参考标准(1)常规标准:25倍合理市盈率。(2)同行业对比。(3)跟历史市盈率相比。 3、PE估值法的适用范围4、PE估值法的优势5、PE估值法的劣势&a…...
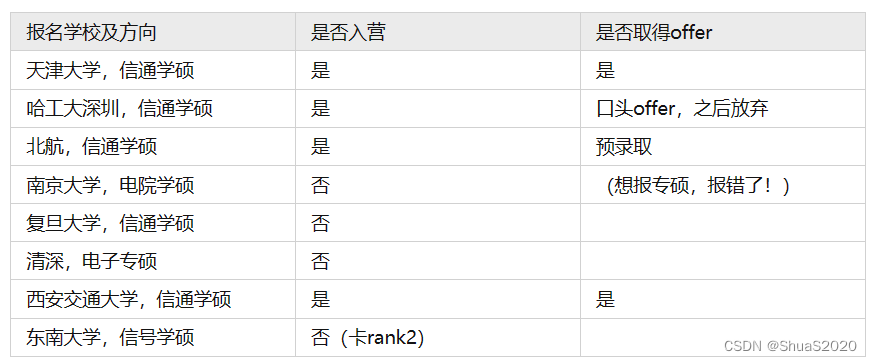
2024届通信工程保研经验分享(预推免入营即offer)
2024届通信工程保研经验分享(预推免入营即offer) BackGround夏令营情况:预推免情况: BackGround 本科院校:末九 专业:通信工程 rank:3/123(预推免绩点排名)࿰…...

L2-025 分而治之 - java
L2-025 分而治之 时间限制 600 ms 内存限制 64 MB 题目描述: 分而治之,各个击破是兵家常用的策略之一。在战争中,我们希望首先攻下敌方的部分城市,使其剩余的城市变成孤立无援,然后再分头各个击破。为此参谋部提供了若…...
Python+高光谱数据预处理-机器学习-深度学习-图像分类-参数回归
涵盖高光谱遥感数据处理的基础、python开发基础、机器学习和应用实践。重点解释高光谱数据处理所涉及的基本概念和理论,旨在帮助学员深入理解科学原理。结合Python编程工具,专注于解决高光谱数据读取、数据预处理、高光谱数据机器学习等技术难题…...

免费 AI 编程助手 Amazon CodeWhisperer 体验
文章作者:文章作者:米菲爸爸 2022 年 6 月 23 亚马逊云科技就已经推出了 Amazon CodeWhisperer(预览版)。经过不到一年的测试和 AIGC的飓风在 2023 年 4 月 18 日实时 AI 编程助手 Amazon CodeWhisperer正式可用 Amazon CodeWhis…...
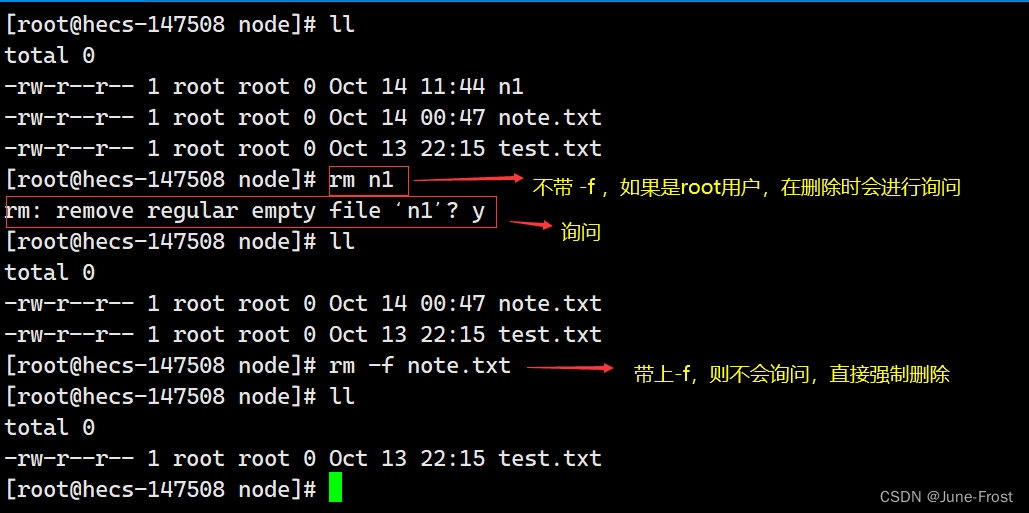
【Linux】从零开始学习Linux基本指令(一)
🚩纸上得来终觉浅, 绝知此事要躬行。 🌟主页:June-Frost 🚀专栏:Linux入门 🔥该文章主要了解Linux操作系统下的基本指令。 目录: ⌛️指令的理解⏳目录和文件的理解⏳一些常见指令✉…...

Java GC 算法
一、概述 理解Java虚拟机垃圾回收机制的底层原理,是成为一个高级Java开发者的基本功。本文从底层的垃圾回收算法开始,着重去阐释不同垃圾回收器在算法设计和实现时的一些技术细节,去探索「why」这一部分,通过对比不同的垃圾回收算…...

vue3 v-html中使用v-viewer
安装:npm install v-viewernext 在main.js中配置 import “viewerjs/dist/viewer.css”; import Viewer from “v-viewer”; app.use(Viewer, { Options: { inline: true, //默认值:false。启用内联模式。 button: true, //在查看器的右上角显示按钮。 …...
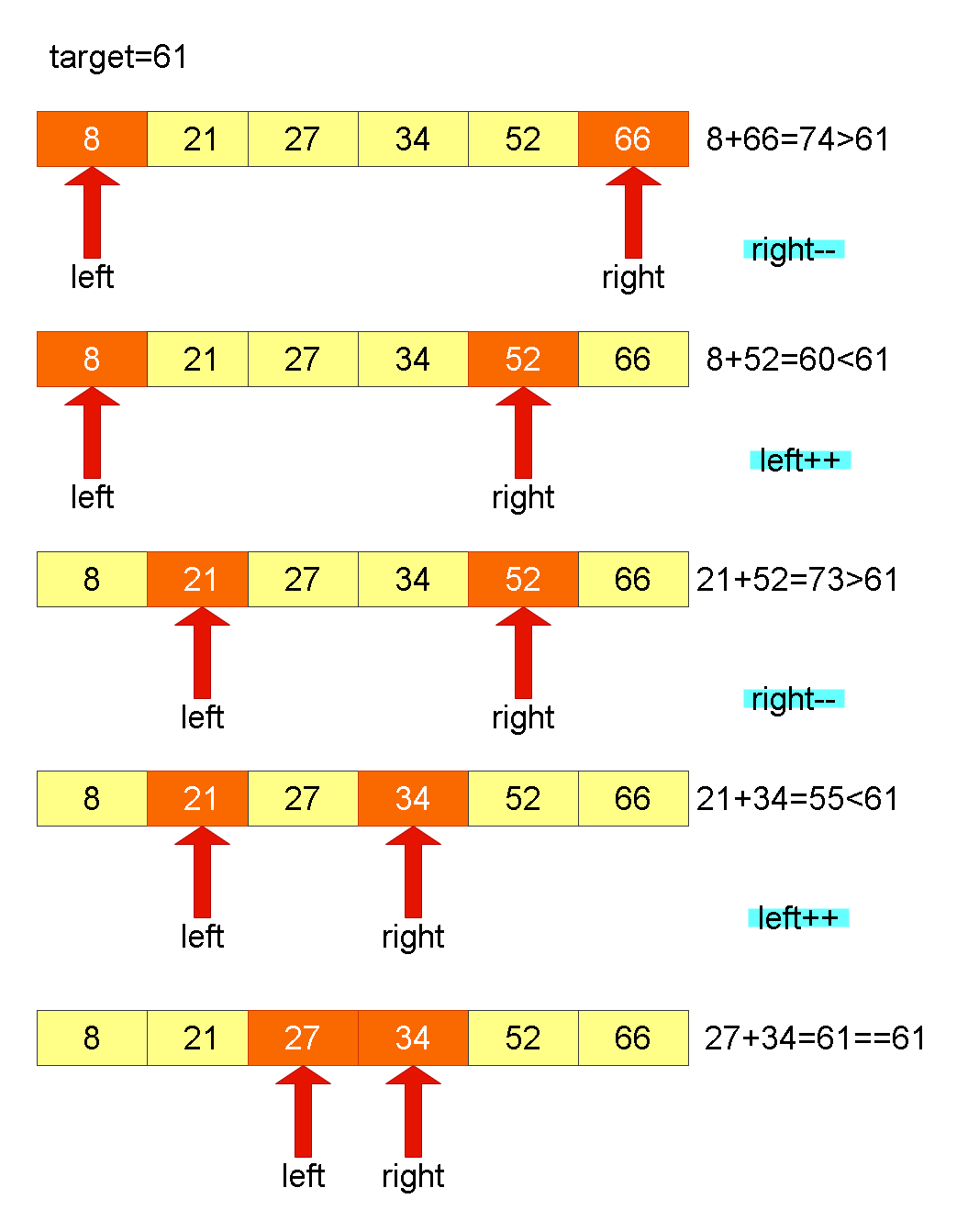
Leetcode算法解析——查找总价格为目标值的两个商品
1. 题目链接:LCR 179. 查找总价格为目标值的两个商品 2. 题目描述: 商品价格按照升序记录于数组 price。请在购物车中找到两个商品的价格总和刚好是 target。若存在多种情况,返回任一结果即可。 示例 1: 输入:price …...

unity游戏开发引擎unity3D开发
Unity(也被称为Unity3D)是一款强大的跨平台游戏引擎,用于开发2D和3D游戏,以及其他交互式应用程序。以下是Unity游戏开发的一般步骤: 安装和设置Unity: 首先,您需要下载并安装Unity。确保选择适…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

AI编程--插件对比分析:CodeRider、GitHub Copilot及其他
AI编程插件对比分析:CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展,AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者,分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...

成都鼎讯硬核科技!雷达目标与干扰模拟器,以卓越性能制胜电磁频谱战
在现代战争中,电磁频谱已成为继陆、海、空、天之后的 “第五维战场”,雷达作为电磁频谱领域的关键装备,其干扰与抗干扰能力的较量,直接影响着战争的胜负走向。由成都鼎讯科技匠心打造的雷达目标与干扰模拟器,凭借数字射…...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...

Python 包管理器 uv 介绍
Python 包管理器 uv 全面介绍 uv 是由 Astral(热门工具 Ruff 的开发者)推出的下一代高性能 Python 包管理器和构建工具,用 Rust 编写。它旨在解决传统工具(如 pip、virtualenv、pip-tools)的性能瓶颈,同时…...

Python ROS2【机器人中间件框架】 简介
销量过万TEEIS德国护膝夏天用薄款 优惠券冠生园 百花蜂蜜428g 挤压瓶纯蜂蜜巨奇严选 鞋子除臭剂360ml 多芬身体磨砂膏280g健70%-75%酒精消毒棉片湿巾1418cm 80片/袋3袋大包清洁食品用消毒 优惠券AIMORNY52朵红玫瑰永生香皂花同城配送非鲜花七夕情人节生日礼物送女友 热卖妙洁棉…...

使用LangGraph和LangSmith构建多智能体人工智能系统
现在,通过组合几个较小的子智能体来创建一个强大的人工智能智能体正成为一种趋势。但这也带来了一些挑战,比如减少幻觉、管理对话流程、在测试期间留意智能体的工作方式、允许人工介入以及评估其性能。你需要进行大量的反复试验。 在这篇博客〔原作者&a…...

深度学习水论文:mamba+图像增强
🧀当前视觉领域对高效长序列建模需求激增,对Mamba图像增强这方向的研究自然也逐渐火热。原因在于其高效长程建模,以及动态计算优势,在图像质量提升和细节恢复方面有难以替代的作用。 🧀因此短时间内,就有不…...
