Javascript自定义页面复制事件
Javascript自定义页面复制事件 – WhiteNight's Site
2023年10月13日
文章访问量:90
标签:Javascript
监听copy事件以达到自定义页面复制功能的效果。
写者注
需要注意的是,浏览器的部分拓展插件(如迅雷)会导致本文的代码报错。不过该报错不影响功能,而且只有在f12开发者控制台才能看见。不过如果觉得看着报错不顺眼的话,关闭导致你报错的拓展即可(自己一个一个试)。
什么是copy事件
用户的复制事件
当用户尝试在页面上复制某些内容时,就会触发copy事件。而通过监听copy事件,我们就可以自定义用户在页面上的复制的内容。比如当用户尝试复制时,出现弹窗或跳转页面(如百度文库);又或者是在用户复制的内容后加上copyright内容(如csdn)。
示例:禁止用户复制,并添加弹窗或跳转页面
代码和效果示例
先放一个能自由输入和复制的文本框在这里,方便调试。
测试文本:
先来实现禁止用户复制的逻辑。这里先放例子。可以试着复制下列文本,再粘贴到上方的文本框中,看看能不能复制成功。
-> 你不能复制该内容 <-
-> 你可以复制该内容 <-
写者注
样式实在不想改,琢磨css样式的话一琢磨就是一整天。还是先把文章完成再说。
上面这段代码实现了对<p>段落标签的监听,当用户尝试复制该内容时,阻止默认的复制事件,并实现你自定义的事件。这里自定义的是修改用户剪贴板的内容,并在浏览器中显示一个警告的弹窗。以下是代码(除去了css)
<div class="copypanel"><p id="content">-> 你不能复制该内容 <-</p><p id="content2">-> 你可以复制该内容 <-</p>
</div><script>content.addEventListener('copy',(e)=>{e.preventDefault();e.clipboardData.setData('text/plain','复制失败!');alert("不准复制!!!")})
</script>那跳转页面也不难实现,直接给实现效果和代码吧。现在当你尝试复制相关内容时,会自动打开我的网站首页。
-> 你不能复制该内容 <-
-> 你可以复制该内容 <-
<div class="copypanel2"><p id="content3">-> 你不能复制该内容 <-</p><p id="content4">-> 你可以复制该内容 <-</p>
</div><script>content3.addEventListener('copy',(e)=>{e.preventDefault();window.open("https://white-night.club"); })
</script>写者注
由于wordpress中自定义html区块就是直接把相关代码直接插入进当前html的一个div容器中,所以如果不指定要监听的元素,会导致当前页面的所有内容都无法访问。想监听当前页面所有dom的话把content换成document.addEventListener即可。
相关文章:

Javascript自定义页面复制事件
Javascript自定义页面复制事件 – WhiteNights Site 2023年10月13日 文章访问量:90 标签:Javascript 监听copy事件以达到自定义页面复制功能的效果。 写者注 需要注意的是,浏览器的部分拓展插件(如迅雷)会导致本文…...
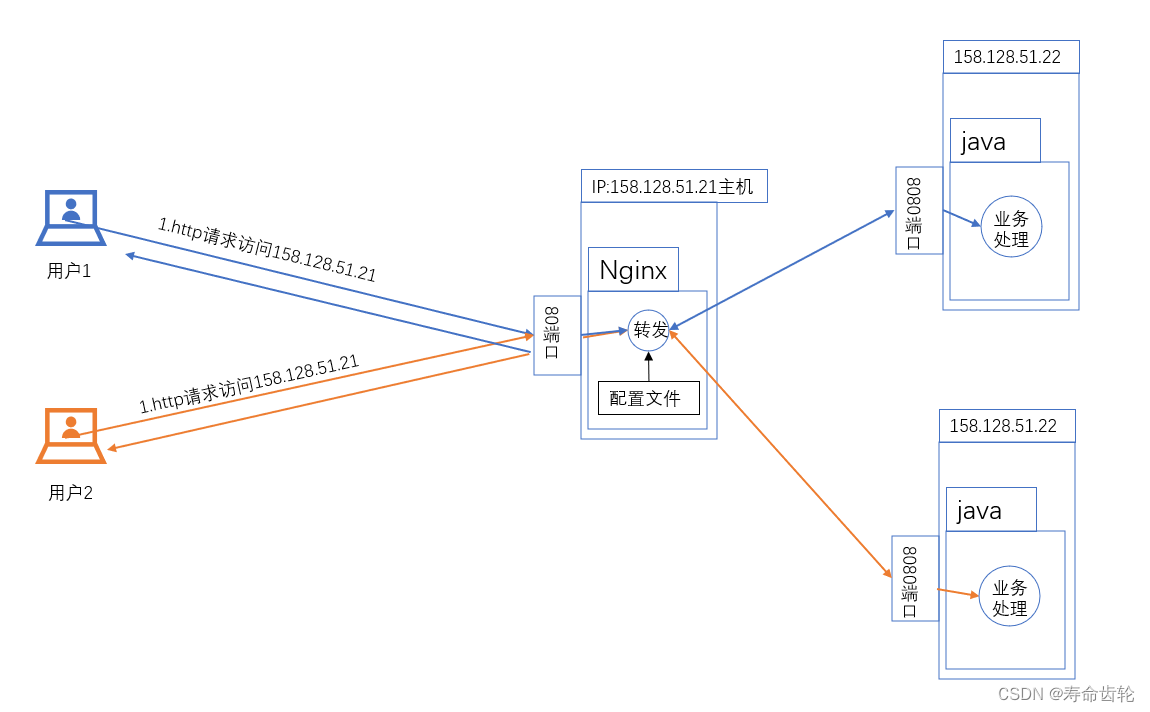
Nginx:反向代理(示意图+配置)
示意图: 反向代理 反向代理(Reverse Proxy)是代理服务器的一种,它代表服务器接收客户端的请求,并将这些请求转发到适当的服务器。当请求在后端服务器完成之后,反向代理搜集请求的响应并将其传输给客户端。…...
macbook笔记本电脑内存怎么清理才能干净流畅?
假如你还在为“你的系统内存不足”的提示所困扰,或者你的Mac电脑突然运行缓慢和卡顿,那么你一般需要认真了解一下macbook内存怎么清理了? MacBook是功能强大的电脑,这点毫无疑问,但是它仍旧会随着时间推移变得运行缓慢。值得庆幸…...

spark 与 mapreduce 对比
Spark 为什么比 MapReduce 快总结 首先澄清几个误区: 1)两者都是基于内存计算的,任何计算框架都肯定是基于内存的,所以说网上所说的 Spark 是基于内存计算所以快,显然是错误的。 2)DAG 计算模型减少的是磁…...
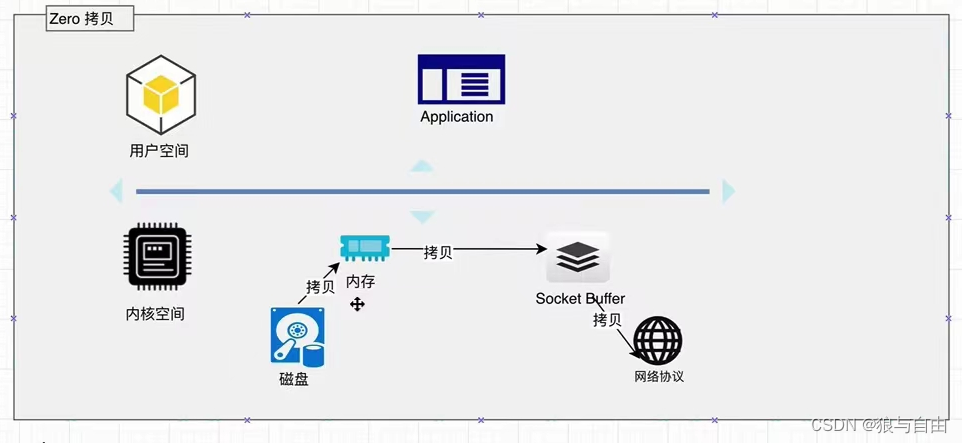
kafka 相关概念
1 kafka 生产者 kafka 用push的方式把消息推送到topic 每个topic下可以有多个分区, 可以用hash 也可以用轮询的方式指定分区 每个分区内部是可以保证顺序的,但是整体无法保证顺序,除非设置成一个topic只有一个分区。 kafka这种多分区的设置 带…...

Ubuntu下vscode配置OpenCV以及Libtorch
opencv安装 sudo apt-get updatesudo apt-get install libopencv-dev 该方式安装的版本可能比较旧。 测试代码 #include <opencv2/opencv.hpp>#include <iostream>int main() {cv::Mat image cv::imread("t.png");cv::imshow("Image", ima…...

关于共识算法Raft的常见误解
关于共识算法Raft的常见误解 Raft 共识算法最终一致性与线性一致性日志的覆盖与删除Remove节点时需要skip 总结参考文档 Raft 共识算法 最近翻了翻Raft相关的资料,同时也总结了日常工作的一些积累,就当做Raft技术笔记吧。 由于工作的关系,Ra…...
Python学习基础笔记七十——模块和库1
模块和库: 一个python代码文件就实现了功能。功能比较单一。 在企业中,项目开发的文件,可能有成百上千个。 不同的代码文件,实现了不同的功能模块,就像一块块积木一样。这些功能文件整合起来,实现一个完…...
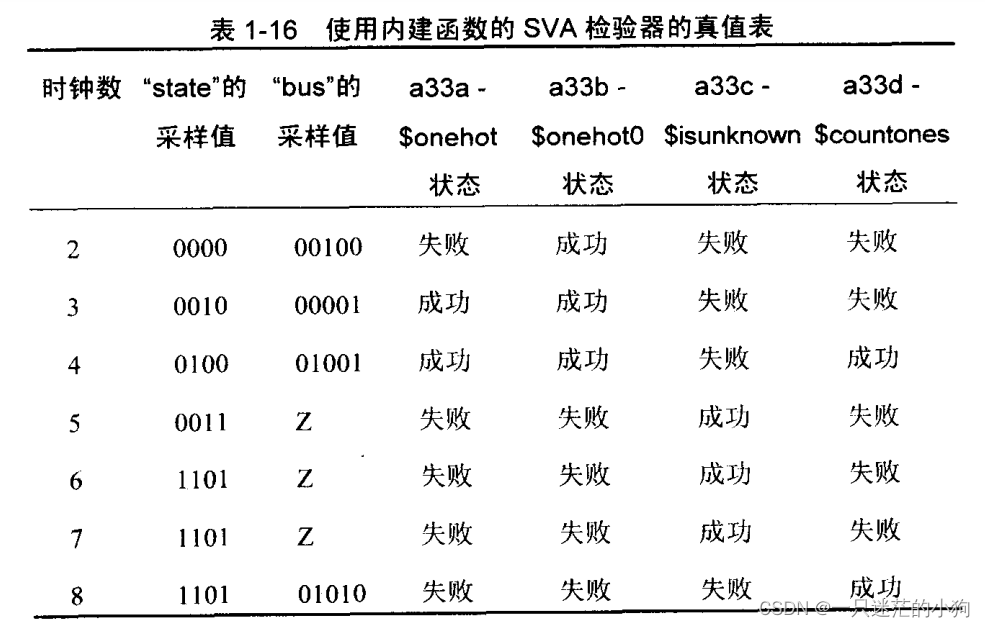
SystemVerilog Assertions应用指南 第一章(1.28章节 内建的系统函数)
SVA提供了几个内建的函数来检查一些最常用的设计条件。 $onehot(expression)—检验表达式满足“one-hot”,换句话说,就是在任意给定的时钟沿,表达式只有一位为高。 $onehot0( expression)—检验表达式满足“ zero one-hot”,换句话说,就是在任意给定…...
)
正则表达式(自用)
正则表达式 符号概述 分类符号用法示例元字符^以 ***开头$以 ***结尾d匹配数字s匹配任意的空白符.匹配除换行符以外的任意字符w匹配字母或数字或下划线或汉字\转义重复限定符*次数,至少一次至少1次?0次 或者 1次{n}{n,}{n,m}重复n次;n活更多次&#x…...

大厂真题:【模拟】OPPO2023秋招提前批-小欧数组求和
题目描述与示例 题目描述 小欧拿到了一个数组,她有q次操作,每次操作修改一个元素。小欧希望每次修改后得到当前数组所有元素之和。你能帮帮她吗? 输入描述 第一行输入两个正整数n和q,代表数组的大小和操作次数。 第二行输入n…...

Python括号匹配问题
给定一个只包含小写字母的字符串,判断该字符串中的括号是否闭合,如果每个左括号都有对应的右括号,并且括号的嵌套顺序正确,那么括号就能正确闭合。 否则,括号不能正确闭合,字符串中括号仅限于 "("…...
微信小程序备案内容常见问题汇总
一、备案时间点 自2023年09月01日起,新的微信小程序,必须备案后才能上架; 在2024年03月31日前,所有小程序都必须完成备案; 于2024年04月01日起,对未备案小程序进行清退处理。 微信小程序备案系统已于9月4日上线。 二、备案流程 [找备案入口]–[填主体信息]–[填小程…...

无人机新手防炸飞行技巧
不要在室内飞行,容易撞墙。起飞前设置好避障和返航模式。使用模拟器熟练掌握操控。选择开阔环境目视起飞。使用低速档平稳飞行。合理使用避障功能,不要盲目依赖。使用九宫格避障法。留意电量,及时返航。极低电量时放弃强行返航。飞行后及时为电池充电保养。...

webrtc opus 音频编码支持SILK和CELT模式
SILK CELT是指将SILK编解码器和CELT编解码器结合在一起的混合音频编码方案。 SILK(Super-wideband audio coding)是一种低延迟的音频编解码器,用于实时的语音通信。它提供高质量的音频传输,并且适用于各种比特率和带宽条件。SILK…...

掌握Python爬虫实现网站关键词扩展提升曝光率
目录 一、关键词优化的重要性 二、关键词优化的基本方法 1、选择与网站内容相关的关键词 2、控制关键词的密度和分布 3、关键词的层次布局 三、Python爬虫实现网站关键词扩展 1、确定目标网站 2、分析目标网站的HTML结构 3、编写Python爬虫代码 4、分析爬取到的关键词…...

ajax实现原理
网页应用能够快速地将增量更新呈现在用户界面上,而不需要重载(刷新)整个页面。这使得程序能够更快地回应用户的操作 Ajax的实现原理 创建Ajax对象 传入请求方式和请求地址 发送请求 获取服务器与客户端的响应数据 xhr.responseText // 1…...

图G的拉普拉斯矩阵为什么由L=D-A定义
图G的拉普拉斯矩阵由LD-A定义,其中D是度矩阵(Degree Matrix),A是邻接矩阵(Adjacency Matrix)。这种定义方式有以下原因: 1. 度矩阵D:度矩阵是一个对角矩阵,其对角线上的…...

实习项目遇到的bug
问题1: 大概是因为没设置ts类型,它查不到的问题,不定义的话加上问号,加上可选链就不会报错了 {{bizEquipmentInfo.lastUnlockingVO?.lastUnlockingTime.replace(T, )? bizEquipmentInfo.lastUnlockingVO?.lastUnlockingTime.r…...
)
python selenium下载一个合适的chromedriver.exe(稳定版本)
可以使用该脚本来进行下载: 下载前需要安装如下的依赖 requests2.27.1 selenium4.14.0 webdriver_manager4.0.1下载脚本代码: import json import subprocess import shutil import os import time import zipfileimport requests from webdriver_mana…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...

Yolov8 目标检测蒸馏学习记录
yolov8系列模型蒸馏基本流程,代码下载:这里本人提交了一个demo:djdll/Yolov8_Distillation: Yolov8轻量化_蒸馏代码实现 在轻量化模型设计中,**知识蒸馏(Knowledge Distillation)**被广泛应用,作为提升模型…...

JVM 内存结构 详解
内存结构 运行时数据区: Java虚拟机在运行Java程序过程中管理的内存区域。 程序计数器: 线程私有,程序控制流的指示器,分支、循环、跳转、异常处理、线程恢复等基础功能都依赖这个计数器完成。 每个线程都有一个程序计数…...

GO协程(Goroutine)问题总结
在使用Go语言来编写代码时,遇到的一些问题总结一下 [参考文档]:https://www.topgoer.com/%E5%B9%B6%E5%8F%91%E7%BC%96%E7%A8%8B/goroutine.html 1. main()函数默认的Goroutine 场景再现: 今天在看到这个教程的时候,在自己的电…...

水泥厂自动化升级利器:Devicenet转Modbus rtu协议转换网关
在水泥厂的生产流程中,工业自动化网关起着至关重要的作用,尤其是JH-DVN-RTU疆鸿智能Devicenet转Modbus rtu协议转换网关,为水泥厂实现高效生产与精准控制提供了有力支持。 水泥厂设备众多,其中不少设备采用Devicenet协议。Devicen…...

归并排序:分治思想的高效排序
目录 基本原理 流程图解 实现方法 递归实现 非递归实现 演示过程 时间复杂度 基本原理 归并排序(Merge Sort)是一种基于分治思想的排序算法,由约翰冯诺伊曼在1945年提出。其核心思想包括: 分割(Divide):将待排序数组递归地分成两个子…...

基于Java项目的Karate API测试
Karate 实现了可以只编写Feature 文件进行测试,但是对于熟悉Java语言的开发或是测试人员,可以通过编程方式集成 Karate 丰富的自动化和数据断言功能。 本篇快速介绍在Java Maven项目中编写和运行测试的示例。 创建Maven项目 最简单的创建项目的方式就是创建一个目录,里面…...
