想要精通算法和SQL的成长之路 - 滑动窗口和大小根堆
想要精通算法和SQL的成长之路 - 滑动窗口和大小根堆
- 前言
- 一. 大小根堆
- 二. 数据流的中位数
- 1.1 初始化
- 1.2 插入操作
- 1.3 完整代码
- 三. 滑动窗口中位数
- 3.1 在第一题的基础上改造
- 3.2 栈的remove操作
前言
想要精通算法和SQL的成长之路 - 系列导航
一. 大小根堆
先来说下大小根堆是什么:

- 大根堆:栈顶元素最大(上图左侧部分),栈底至栈顶元素值递增。
- 小根堆:栈顶元素最小(上图右侧部分),栈底至栈顶元素值递减。
在Java当中,可以用什么来表示大小根堆?
小根堆:
Queue<Integer> small = new PriorityQueue<>();
// 或者 x - y 是计算,在特殊情况下可能造成精度越界的情况
Queue<Integer> small = new PriorityQueue<>((x, y) -> x - y);
// 或者,Integer.compare 是纯比较,不会出现精度越界
Queue<Integer> small = new PriorityQueue<>((x, y) -> Integer.compare(x, y));
// 或者
Queue<Integer> small = new PriorityQueue<>(Integer::compare);
大根堆:
Queue<Integer> big = new PriorityQueue<>((x, y) -> y - x);
大小根堆的常规操作:
- 获取栈顶元素:
peek(); - 栈顶元素移除:
poll();
二. 数据流的中位数
原题链接


再说下我们的思路:
- 同时维护大小根堆,并且约定小根堆的元素个数总是 >= 大根堆元素个数(最多个数多一个)。
- 如果元素个数是奇数,那么中位数就是小根堆堆顶元素。
- 如果元素个数是偶数,那么中位数就是(大根堆堆顶 + 小根堆堆顶) / 2。
1.1 初始化
Queue<Integer> big, small;/*** big small* 最小值 ---> 大根堆顶 中位数 小根堆顶 ---> 最大值*/
public MedianFinder() {small = new PriorityQueue<>();// 小根堆,堆顶元素最小(存储比中位数大的部分)big = new PriorityQueue<>((x, y) -> y - x);// 大根堆,堆顶元素最大(存储比中位数小的部分)
}
1.2 插入操作
插入的时候,我们考虑到两种情况:
- 如果大小根堆的元素个数相等,我们优先把新元素加入到小根堆。
- 否则,将元素加入到大根堆。
但是,我们并不知道以下三者的关系:
- 大根堆堆顶元素值。
- 当前待加入元素值。
- 小根堆堆顶元素值。
而我们需要去维护他们,一定满足:大根堆堆顶元素值 < 小根堆堆顶元素值。
咋办呢?以第一种情况为例,我们可以:
- 先把元素加入到大根堆。那么经过排序后,大根堆的堆顶元素就是最大的那个(可能是当前元素,也可能不是)。此时大根堆
Size> 小根堆Size。 - 把大根堆堆顶元素移除,加入到小根堆。小根堆经过排序后,这样就能保证大根堆堆顶元素值 < 小根堆堆顶元素值。
写成代码就是:
public void addNum(int num) {// 如果大小根堆 的 大小 一样,我们往小根堆放元素。让小根堆size >= 大根堆sizeif (big.size() == small.size()) {// 方式一定是先让放大根堆,再把大根堆的堆顶元素移除到小根堆big.add(num);small.add(big.poll());} else {small.add(num);big.add(small.poll());}
}
1.3 完整代码
那么查询函数就更简单了,结合上面的思路,我们得到完整代码如下:
public class MedianFinder {Queue<Integer> big, small;/*** big small* 最小值 ---> 大根堆顶 中位数 小根堆顶 ---> 最大值*/public MedianFinder() {small = new PriorityQueue<>();// 小根堆,堆顶元素最小(存储比中位数大的部分)big = new PriorityQueue<>((x, y) -> y - x);// 大根堆,堆顶元素最大(存储比中位数小的部分)}public void addNum(int num) {// 如果大小根堆 的 大小 一样,我们往小根堆放元素。让小根堆size >= 大根堆sizeif (big.size() == small.size()) {// 方式一定是先让放大根堆,再把大根堆的堆顶元素移除到小根堆big.add(num);small.add(big.poll());} else {small.add(num);big.add(small.poll());}}public double findMedian() {return small.size() == big.size() ? (small.peek() + big.peek()) / 2.0 : small.peek();}
}
三. 滑动窗口中位数
原题链接
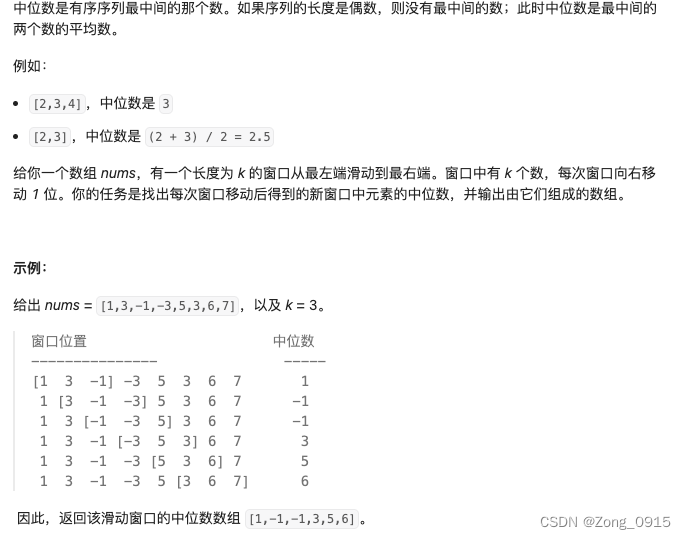
思路如下:
- 我们先创建一个窗口,把前k个数字通过大小根堆的方式去维护(题目一的思路)。
- 后续每次滑动窗口的移动,都带来两个变数:一个旧元素会从窗口出移除(但是从大根堆移除还是小根堆移除?),一个新元素会加入到窗口中(加入到大根堆还是小根堆?)
- 由于第二步的变数,可能导致大小根堆的
Size不均衡。我们的目的:让小根堆的Size>= 大根堆Size,最多多一个元素。 - 因此每次滑动窗口的移动,我们还需要维护大小根堆。
3.1 在第一题的基础上改造
首先考虑到精度的问题,我们的大小根堆不能在根据差值来比较了,而是:
right = new PriorityQueue<>((x, y) -> Integer.compare(x, y));// 小根堆,堆顶元素最小(存储比中位数大的部分)
left = new PriorityQueue<>((x, y) -> Integer.compare(y, x));// 大根堆,堆顶元素最大(存储比中位数小的部分)
其次,求中位数的时候,也需要大小根堆的堆顶元素,先除以2,再和相加:
if (left.size() == right.size()) {return (left.peek() / 2.0) + (right.peek() / 2.0);
最终代码如下:
public class Test480 {Queue<Integer> left, right;public double[] medianSlidingWindow(int[] nums, int k) {right = new PriorityQueue<>((x, y) -> Integer.compare(x, y));// 小根堆,堆顶元素最小(存储比中位数大的部分)left = new PriorityQueue<>((x, y) -> Integer.compare(y, x));// 大根堆,堆顶元素最大(存储比中位数小的部分)int len = nums.length;// 结果集double[] res = new double[len - k + 1];// 创建大小根堆for (int i = 0; i < k; i++) {right.add(nums[i]);}for (int i = 0; i < k / 2; i++) {left.add(right.poll());}// 初始化第一个中位数res[0] = findMedian();for (int i = k; i < len; i++) {// 滑动窗口长度固定,每次移动,都有一个元素要删除和一个元素要新加入int del = nums[i - k], add = nums[i];if (add >= right.peek()) {right.add(add);} else {left.add(add);}// 如果待删除元素在小根堆,在小根堆处删除,否则在大根堆中删除if (del >= right.peek()) {right.remove(del);} else {left.remove(del);}// 维护大小根堆的元素个数adjust();res[i - k + 1] = findMedian();}return res;}void adjust() {while (left.size() > right.size()) {right.add(left.poll());}while (right.size() - left.size() > 1) {left.add(right.poll());}}public double findMedian() {if (left.size() == right.size()) {return (left.peek() / 2.0) + (right.peek() / 2.0);} else {return right.peek() * 1.0;}}
}
这个写法其实是没问题的,但是在元素个数非常大的情况下,就容易超时:
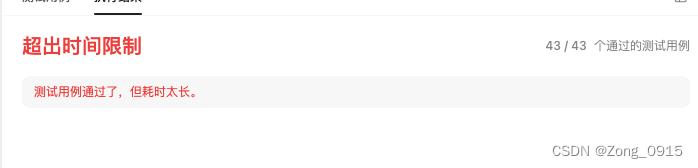
3.2 栈的remove操作
问题处在优先队列的的一个元素remove操作:
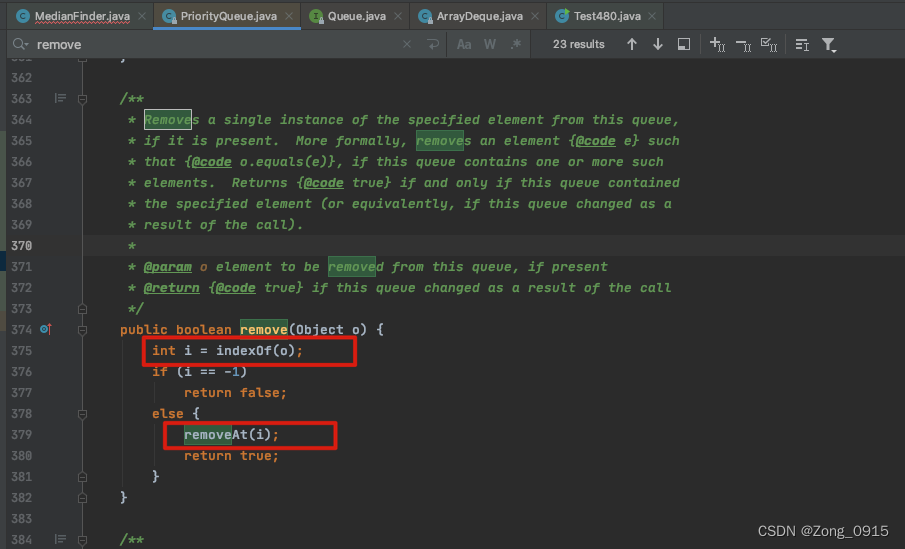
它是先查找(复杂度O(N)),再进行删除(复杂度O(logN)),所以会超时。因此我们这里可以引入红黑树来进行替代。
有这么几个需要注意的地方:
- 我们用
TreeSet存储元素的时候,不再是元素值,而是元素的下标。 因为题目中同一个窗口的元素可能重复。元素值相等的时候,根据下标大小来比较。
Comparator<Integer> comparator = (x, y) -> nums[x] != nums[y] ? Integer.compare(nums[x], nums[y]) : x - y;
right = new TreeSet<>(comparator);// 小根堆,堆顶元素最小(存储比中位数大的部分)
left = new TreeSet<>(comparator.reversed());// 大根堆,堆顶元素最大(存储比中位数小的部分)
- 滑动窗口移动的时候。需要删除对应的元素下标 ,由于存在重复值,我们需要大小根堆都把这个下标给剔除。
- 原
peek函数替代为first函数。poll函数替代为pollFirst函数。
完整代码如下:
public class Test480 {TreeSet<Integer> left, right;int[] nums;public double[] medianSlidingWindow(int[] nums, int k) {this.nums = nums;Comparator<Integer> comparator = (x, y) -> nums[x] != nums[y] ? Integer.compare(nums[x], nums[y]) : x - y;right = new TreeSet<>(comparator);// 小根堆,堆顶元素最小(存储比中位数大的部分)left = new TreeSet<>(comparator.reversed());// 大根堆,堆顶元素最大(存储比中位数小的部分)int len = nums.length;// 结果集double[] res = new double[len - k + 1];// 创建大小根堆for (int i = 0; i < k; i++) {addToWindow(i);}res[0] = findMedian();for (int i = k; i < len; i++) {// 滑动窗口长度固定,每次移动,都有一个元素要删除和一个元素要新加入left.remove(i - k);right.remove(i - k);addToWindow(i);res[i - k + 1] = findMedian();}return res;}void addToWindow(int index) {// 我们总是把新元素先统一加入到大根堆。right.add(index);left.add(right.pollFirst());// 然后再维护大小while (left.size() > right.size()) {right.add(left.pollFirst());}}public double findMedian() {if (left.size() == right.size()) {return (nums[left.first()] / 2.0) + (nums[right.first()] / 2.0);} else {return nums[right.first()] * 1.0;}}
}
相关文章:

想要精通算法和SQL的成长之路 - 滑动窗口和大小根堆
想要精通算法和SQL的成长之路 - 滑动窗口和大小根堆 前言一. 大小根堆二. 数据流的中位数1.1 初始化1.2 插入操作1.3 完整代码 三. 滑动窗口中位数3.1 在第一题的基础上改造3.2 栈的remove操作 前言 想要精通算法和SQL的成长之路 - 系列导航 一. 大小根堆 先来说下大小根堆是什…...
Python算法练习 10.15
leetcode 2130 链表的最大孪生和 在一个大小为 n 且 n 为 偶数 的链表中,对于 0 < i < (n / 2) - 1 的 i ,第 i 个节点(下标从 0 开始)的孪生节点为第 (n-1-i) 个节点 。 比方说,n 4 那么节点 0 是节点 3 的孪…...

智能防眩目前照灯系统控制器ADB
经纬恒润的自适应远光系统—— ADB(Adaptive Driving Beam) 是一种能够根据路况自适应变换远光光型的智能远光控制系统。根据本车行驶状态、环境状态以及道路车辆状态,ADB 系统自动为驾驶员开启或退出远光。同时,根据车辆前方视野…...
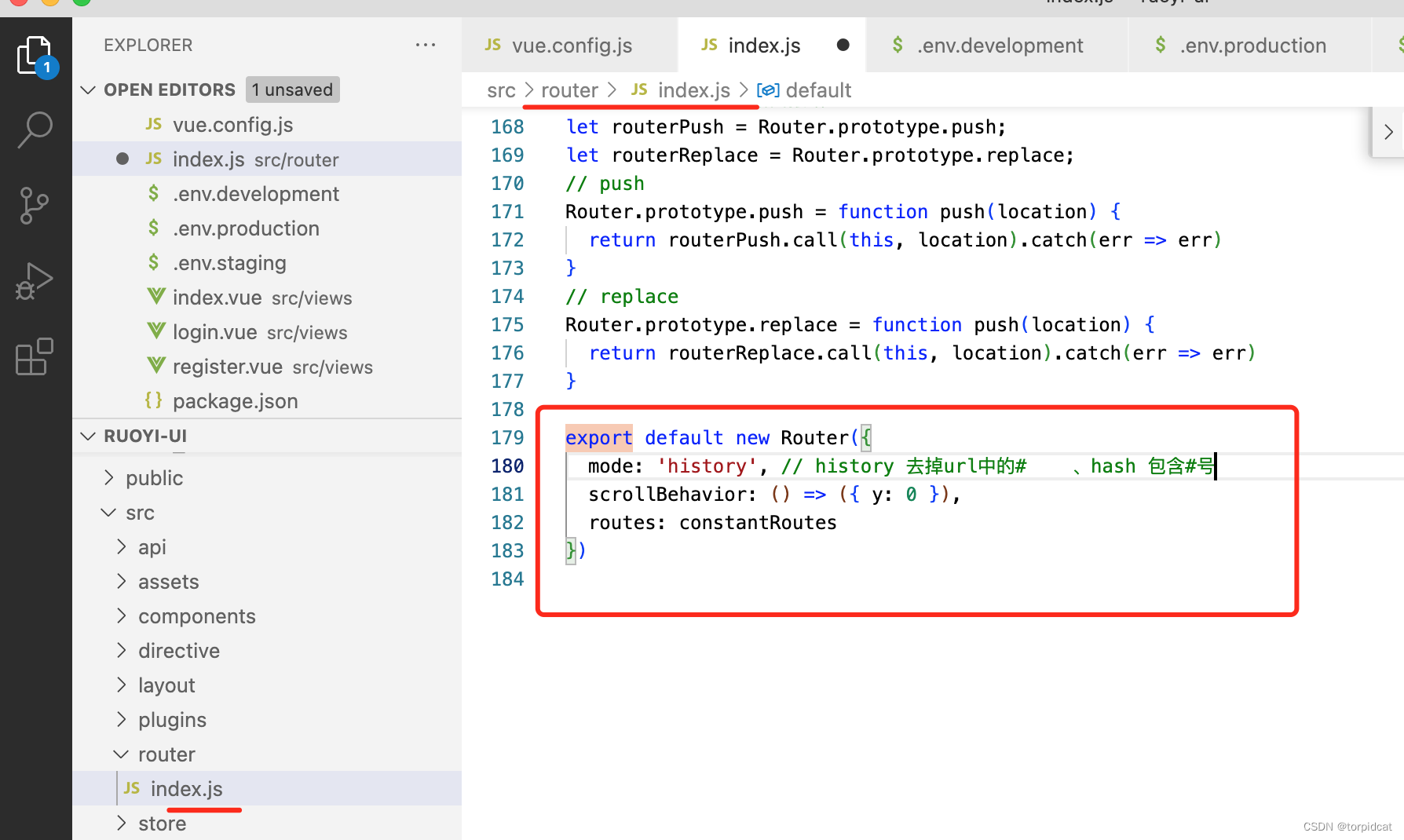
若依 ruoyi 路径 地址 # 井号去除
export default new Router({mode: history, // history 去掉url中的# 、hash 包含#号scrollBehavior: () > ({ y: 0 }),routes: constantRoutes })...
Elasticsearch 和 Arduino:一起变得更好!
作者:Enrico Zimuel 使用 Arduino IoT 设备与 Elasticsearch 和 Elastic Cloud 进行通信的简单方法 在 Elastic,我们不断寻找简化搜索体验的新方法,并开始关注物联网世界。 来自物联网的数据收集可能非常具有挑战性,尤其是当我们…...

基于Ubuntu环境Git 服务器搭建及使用
多人合作开发的时候 常常会需要使用代码管理平台,保持代码一致和解决冲突。在工作中我使用过SVN和TFS,本文说明另外一种平台,Git,下面是基于Ubuntu环境安装并简单使用Git服务器。 确认安装git apt install git levilevi-ThinkPa…...
【quartus13.1/Verilog】swjtu西南交大:计组课程设计
实验目的: 通过学习简单的指令系统及其各指令的操作流程,用 Verilog HDL 语言实 现简单的处理器模块,并通过调用存储器模块,将处理器模块和存储器模块连接形成简 化的计算机核心部件组成的系统。 二. 实验内容 1. 底层用 Verilog…...

基于springboot的网上点餐系统论文开题报告
一、选题背景 随着互联网和移动互联网技术的快速发展,网上点餐成为了人们越来越喜欢的一种点餐方式。一些具有创新意识的餐厅也开始逐渐尝试利用互联网技术来提升用户的点餐体验。因此,开发一个基于Spring Boot的网上点餐系统就显得非常必要和重要。 二…...
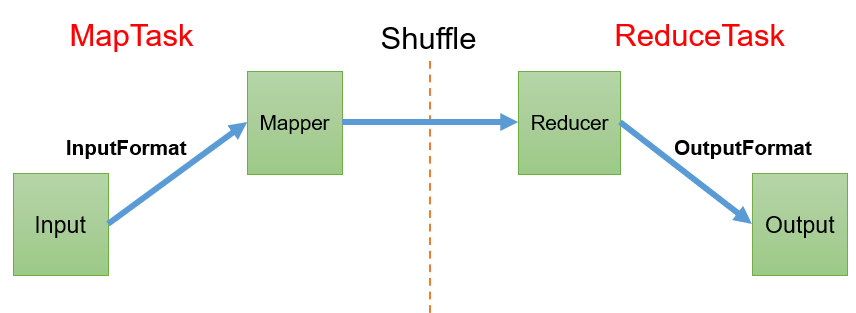
Hadoop3教程(九):MapReduce框架原理概述
文章目录 简介参考文献 简介 这属于整个MR中最核心的一块,后续小节会展开描述。 整个MR处理流程,是分为Map阶段和Reduce阶段。 一般,我们称Map阶段的进程是MapTask,称Reduce阶段是ReduceTask。 其完整的工作流程如图ÿ…...

使用PyTorch加载数据集:简单指南
💗💗💗欢迎来到我的博客,你将找到有关如何使用技术解决问题的文章,也会找到某个技术的学习路线。无论你是何种职业,我都希望我的博客对你有所帮助。最后不要忘记订阅我的博客以获取最新文章,也欢…...
)
【考研数学】线性代数第六章 —— 二次型(2,基本定理及二次型标准化方法)
文章目录 引言一、二次型的基本概念及其标准型1.2 基本定理1.3 二次型标准化方法1. 配方法2. 正交变换法 写在最后 引言 了解了关于二次型的基本概念以及梳理了矩阵三大关系后,我们继续往后学习二次型的内容。 一、二次型的基本概念及其标准型 1.2 基本定理 定理…...
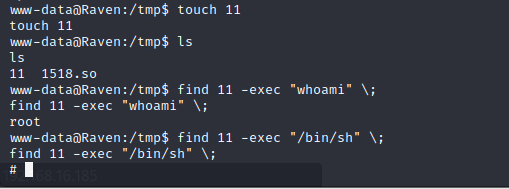
Raven2靶机渗透
1. 信息收集 1.1 主机探测 sudo arp-scan -l1.2 端口扫描 nmap -p- -A 192.168.16.185开放了80端口,尝试登录网址查看信息,通过浏览器插件找出指纹 1.3 目录扫描 访问登录界面,发现remember Me怀疑是shiro界面 登录/vendor/界面࿰…...

UE5中双pass解决半透明材质乱序问题
透明度材质乱序问题一直是半透明效果时遇到的比较多的问题,用多pass方案只能说一定程度上解决,当遇到多半透明物体穿插等情况时,仍然不能完美解决。 双pass方案Unity用的比较多,因为Unity支持多个pass绘制。在UE中我们可以以复制多…...
Cisdem Video Player for mac(高清视频播放器) v5.6.0中文版
Cisdem Video Player mac是一款功能强大的视频播放器,适用于 macOS 平台。它可用于播放不同格式的视频文件,并具有一些实用的特性和功能。 Cisdem Video Player mac 中文版软件特点 多格式支持:Cisdem Video Player 支持几乎所有常见的视频格…...

数据库管理-第109期 19c OCM考后感(20231015)
数据库管理-第109期 19c OCM考后感(202301015) 距离上一篇又过了两周多,为啥又卡了这么久,主要是后面几个问题:1. 9月1日的19c OCM upgrade考试木有过,因为有一次免费补考机会就又预约了10月8日的考试&…...
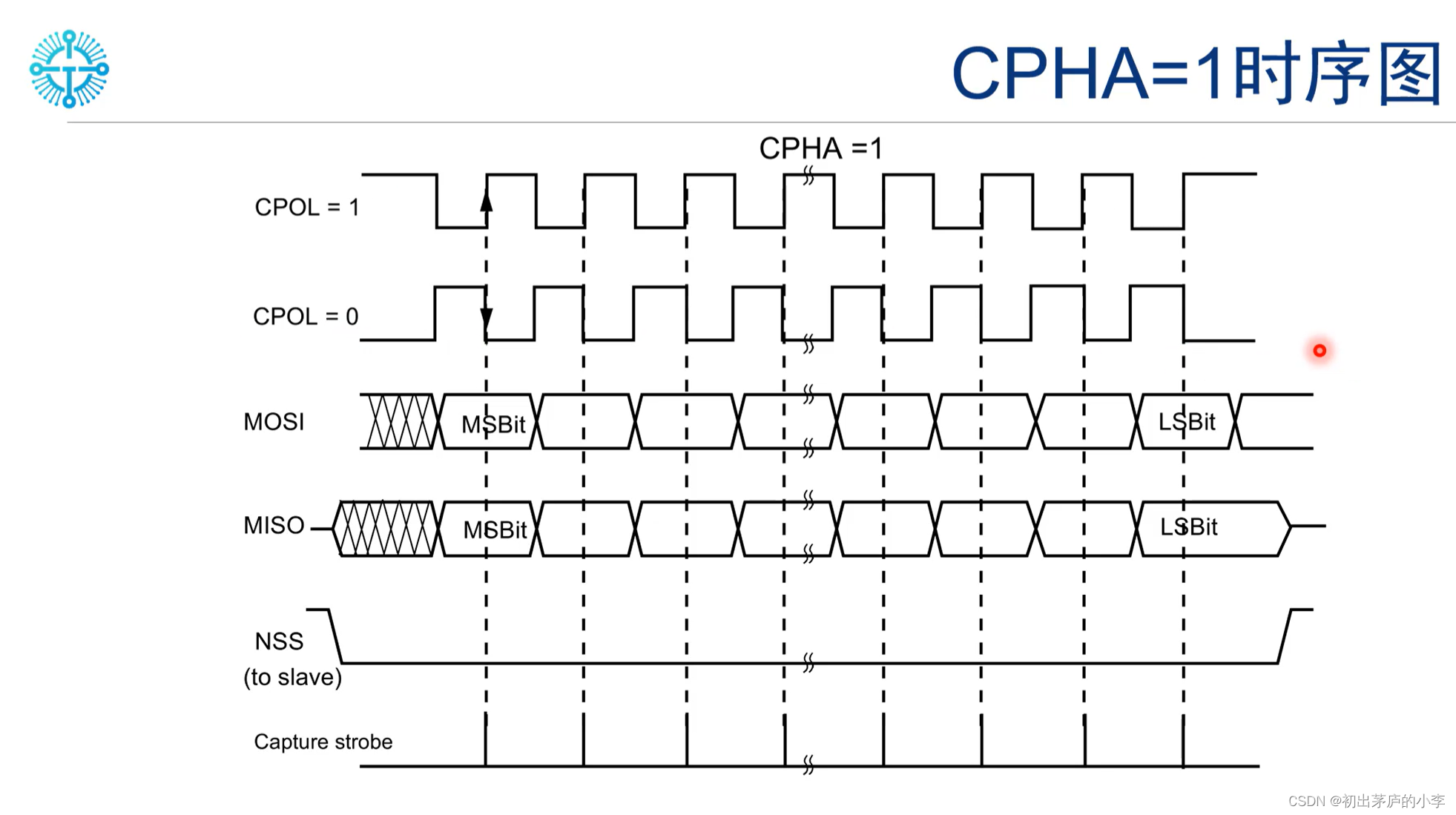
初出茅庐的小李博客之SPI工作模式
SPI的工作模式 SPI(Serial Peripheral Interface)是一种同步串行通信协议,常用于连接微控制器和外围设备。SPI有四种模式,分别是0、1、2、3模式。 0模式:时钟空闲时为低电平,数据在时钟的下降沿采样&#…...

SpringCloud-Bus
一、介绍 (1)bus搭配config可以实现客户端配置自动刷新 (2)bus支持两种消息代理,rabbitmq和kafka (3)使用topic模式分发消息 二、项目搭建(广播) (1&#…...
Adobe2024 全家桶更新了,PS、Ai、AE、PR应用尽有
Adobe2024 全家桶更新了,包含的PS、Ai、AE、PR......个人学习,专业领域都是必不可少的软件都有,需要的不要错过了。 如果你不知道从哪里安装这些工具,小编为大家带来了破J版资源,附上详细的安装包及安装教程。 Mac软件…...

【斗破年番】彩鳞换装美翻,雁落天惨死,萧炎暗杀慕兰三老遇险,彩鳞霸气护夫
Hello,小伙伴们,我是小郑继续为大家深度解析斗破苍穹年番资讯。 斗破苍穹动画已经更新了,小医仙与萧炎相认,三国联军撤退,随后彩鳞与萧炎以及小医仙夜晚相会,一起制定了刺杀行动。从官方公布的第68集预告,彩…...

华为端到端战略管理体系(DSTE开发战略到执行)的运作日历图/逻辑图及DSTE三大子流程介绍
华为端到端战略管理体系(DSTE开发战略到执行)的运作日历图/逻辑图及DSTE三大子流程介绍 本文作者 | 谢宁,《华为战略管理法:DSTE实战体系》、《智慧研发管理》作者 添加图片注释,不超过 140 字(可选&#…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

【从零学习JVM|第三篇】类的生命周期(高频面试题)
前言: 在Java编程中,类的生命周期是指类从被加载到内存中开始,到被卸载出内存为止的整个过程。了解类的生命周期对于理解Java程序的运行机制以及性能优化非常重要。本文会深入探寻类的生命周期,让读者对此有深刻印象。 目录 …...

【C++特殊工具与技术】优化内存分配(一):C++中的内存分配
目录 一、C 内存的基本概念 1.1 内存的物理与逻辑结构 1.2 C 程序的内存区域划分 二、栈内存分配 2.1 栈内存的特点 2.2 栈内存分配示例 三、堆内存分配 3.1 new和delete操作符 4.2 内存泄漏与悬空指针问题 4.3 new和delete的重载 四、智能指针…...

MySQL JOIN 表过多的优化思路
当 MySQL 查询涉及大量表 JOIN 时,性能会显著下降。以下是优化思路和简易实现方法: 一、核心优化思路 减少 JOIN 数量 数据冗余:添加必要的冗余字段(如订单表直接存储用户名)合并表:将频繁关联的小表合并成…...

如何应对敏捷转型中的团队阻力
应对敏捷转型中的团队阻力需要明确沟通敏捷转型目的、提升团队参与感、提供充分的培训与支持、逐步推进敏捷实践、建立清晰的奖励和反馈机制。其中,明确沟通敏捷转型目的尤为关键,团队成员只有清晰理解转型背后的原因和利益,才能降低对变化的…...

LangFlow技术架构分析
🔧 LangFlow 的可视化技术栈 前端节点编辑器 底层框架:基于 (一个现代化的 React 节点绘图库) 功能: 拖拽式构建 LangGraph 状态机 实时连线定义节点依赖关系 可视化调试循环和分支逻辑 与 LangGraph 的深…...

十九、【用户管理与权限 - 篇一】后端基础:用户列表与角色模型的初步构建
【用户管理与权限 - 篇一】后端基础:用户列表与角色模型的初步构建 前言准备工作第一部分:回顾 Django 内置的 `User` 模型第二部分:设计并创建 `Role` 和 `UserProfile` 模型第三部分:创建 Serializers第四部分:创建 ViewSets第五部分:注册 API 路由第六部分:后端初步测…...

ZYNQ学习记录FPGA(一)ZYNQ简介
一、知识准备 1.一些术语,缩写和概念: 1)ZYNQ全称:ZYNQ7000 All Pgrammable SoC 2)SoC:system on chips(片上系统),对比集成电路的SoB(system on board) 3)ARM:处理器…...
