机器学习-有监督算法-决策树和支持向量机
目录
- 决策树
- ID3
- C4.5
- CART
- 支持向量积
决策树
- 训练:构造树,测试:从模型从上往下走一遍。
- 建树方法:ID3,C4.5,CART
ID3
- 以信息论为基础,以信息增益为衡量标准
- 熵越小,混乱程度越小,不确定性越小
- 信息熵:
H ( D ) = − ∑ i = 1 n P ( D i ) log 2 P ( D i ) H(D) = -\sum_{i=1}^{n} P(D_i) \log_{2} P(D_i) H(D)=−i=1∑nP(Di)log2P(Di) - 条件熵:
H ( D ∣ A ) = − ∑ i = 1 n ∣ D i ∣ ∣ D ∣ log 2 ( ∣ D i ∣ ∣ D ∣ ) H(D|A) = -\sum_{i=1}^{n} \frac{|D_i|}{|D|} \log_{2} \left(\frac{|D_i|}{|D|}\right) H(D∣A)=−i=1∑n∣D∣∣Di∣log2(∣D∣∣Di∣) - 信息增益:
G ( D , A ) = H ( D ) − H ( D ∣ A ) G(D,A) = H(D) - H(D|A) G(D,A)=H(D)−H(D∣A) - 步骤
- 求特征对最后结果的信息熵,条件熵,和最后的信息增益
- 选择信息增益最大的作为当前决策节点
- 删除上一步使用的特征,用特征值划分不同的数据集合
- 重复2,3步
C4.5
- ID3算法的改进
- 利用信息增益率:
G R ( D , A ) = G ( D , A ) H ( D ) G_R(D,A) = \frac{G(D,A)}{H(D)} GR(D,A)=H(D)G(D,A) - 预剪枝:边建树边剪枝,限制深度、叶子节点个数、叶子结点样本数、信息增益率
- 后剪枝:建完树剪枝。用叶子节点替换非叶子节点,然后判断错误率是保持还是下降
CART
- 分类树利用基尼指数来进行分类,分类树最后叶子节点众数作为结果。
- 回归树利用方差来进行分类,利用特征划分成子集后,各自自己方差要最小,总体方差和也要最小。回归树用最后的均值或中位数作为结果。
支持向量积
- 解决问题:什么样的分类结果最好
- 监督学习、分类算法
- 距离定义,决策面,优化目标
- 拉格朗日乘子法
- 软间隔
- 核变换
相关文章:

机器学习-有监督算法-决策树和支持向量机
目录 决策树ID3C4.5CART 支持向量积 决策树 训练:构造树,测试:从模型从上往下走一遍。建树方法:ID3,C4.5,CART ID3 以信息论为基础,以信息增益为衡量标准熵越小,混乱程度越小&…...

luffy项目之后台项目搭建、目录调整、封装日志、全局异常、Response、数据库连接
luffy后台项目创建 在虚拟环境中创建luffy项目安装django:pip install django3.1.12命令创建项目django-admin startproject luffy_api也可以pycharm创建项目,创建项目时选则已经创建好的虚拟环境即可 luffy项目目录调整 """ ├── …...
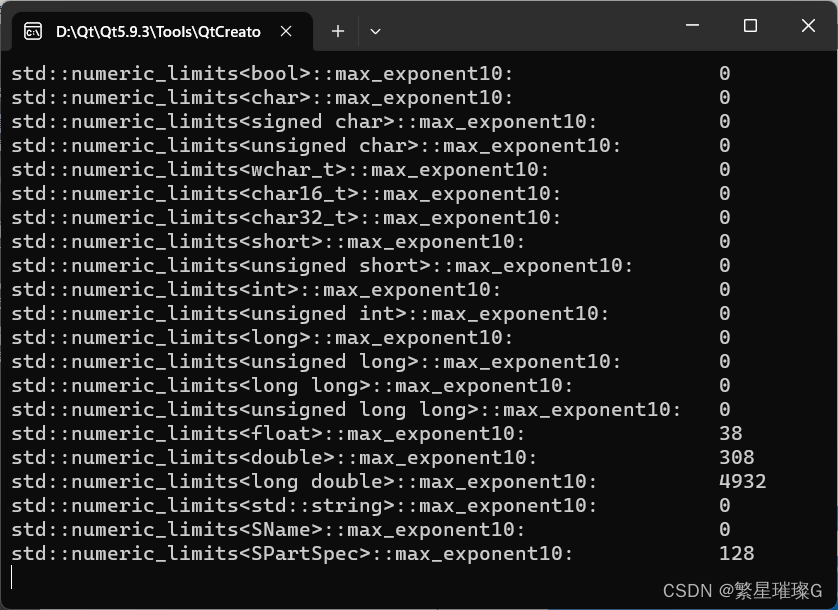
C++标准模板(STL)- 类型支持 (数值极限,min_exponent10,max_exponent,max_exponent10)
数值极限 std::numeric_limits 定义于头文件 <limits> 定义于头文件 <limits> template< class T > class numeric_limits; numeric_limits 类模板提供查询各种算术类型属性的标准化方式(例如 int 类型的最大可能值是 std::numeric_limits&l…...
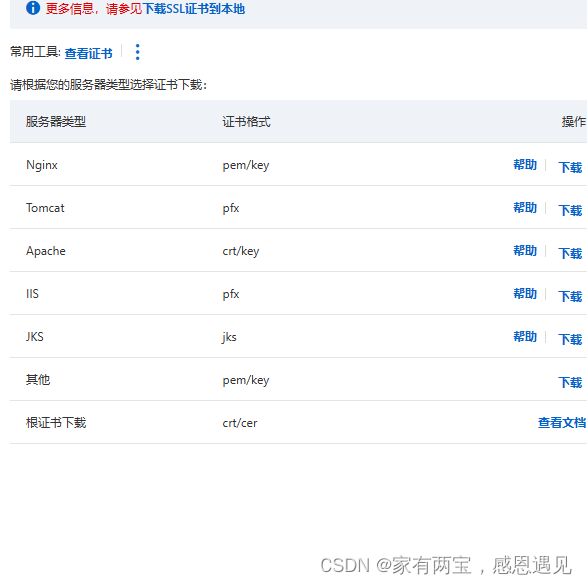
linux 服务器类型Apache配置https访问
一:查看服务器类型,下载相应的SSL证书 命令:netstat -anp | grep :80 httpd是Apache超文本传输协议(HTTP)服务器的主程序,所以下载Apache证书 二:将证书解压后复制到服务器上 三个文件:xxx.key xxx_publ…...
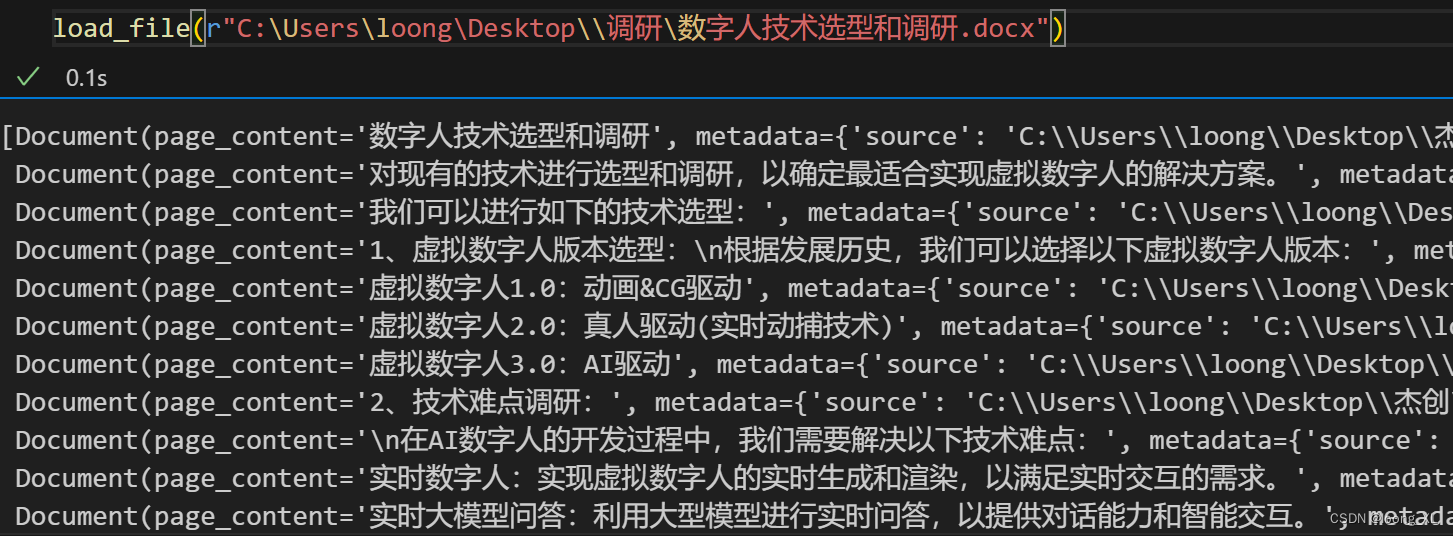
langchain 加载各种格式文件读取方法
参考:https://python.langchain.com/docs/modules/data_connection/document_loaders/ https://github.com/thomas-yanxin/LangChain-ChatGLM-Webui/blob/master/app.py 代码 可以支持pdf、md、doc、txt等格式 from langchain.document_loaders import Unstruct…...
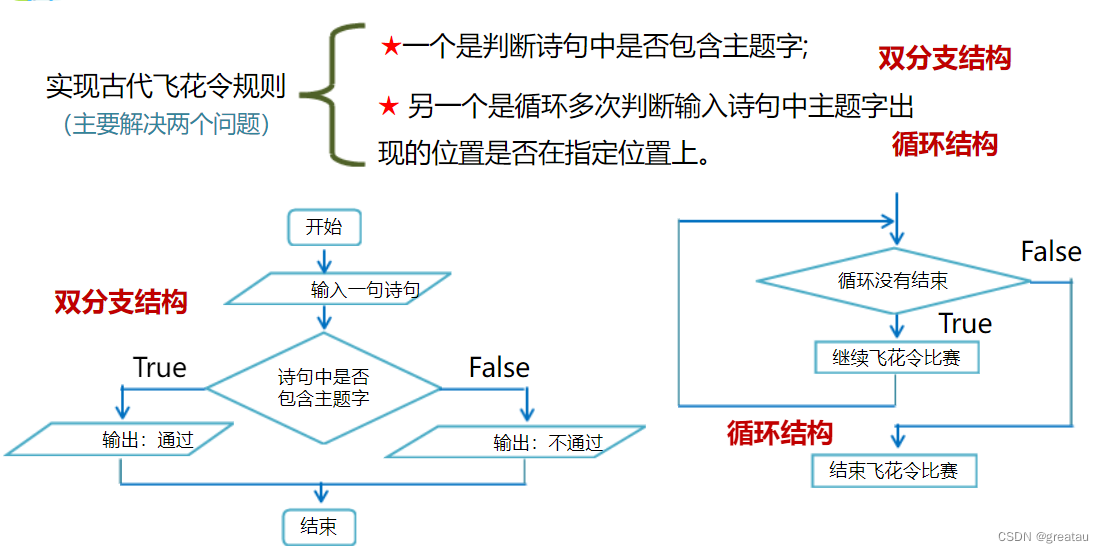
飞花令游戏(Python)
飞花令是古时候人们经常玩一种“行酒令”的游戏,是中国古代酒令之一,属雅令。“飞花”一词则出自唐代诗人韩翃《寒食》中 春城无处不飞花 一句。行飞花令时选用诗和词,也可用曲,但选择的句子一般不超过7个字。 在《中国诗词大会》…...
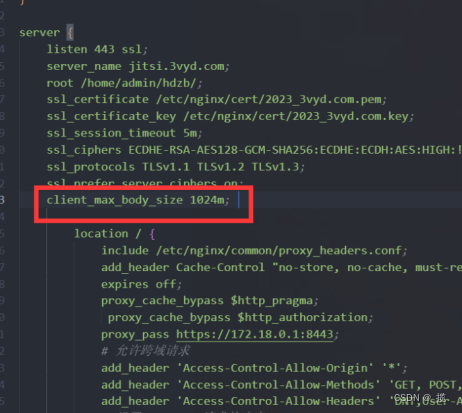
解决“413 Request Entity Too Large”错误 代表请求包太大,服务器拒绝响应
解决办法: 在nginx的配置文件nginx.conf中,添加这么一句client_max_body_size 1024m; 意思是最大请求是1024m。这个配置可以放到 http段 或者 server段 或者 location段。...
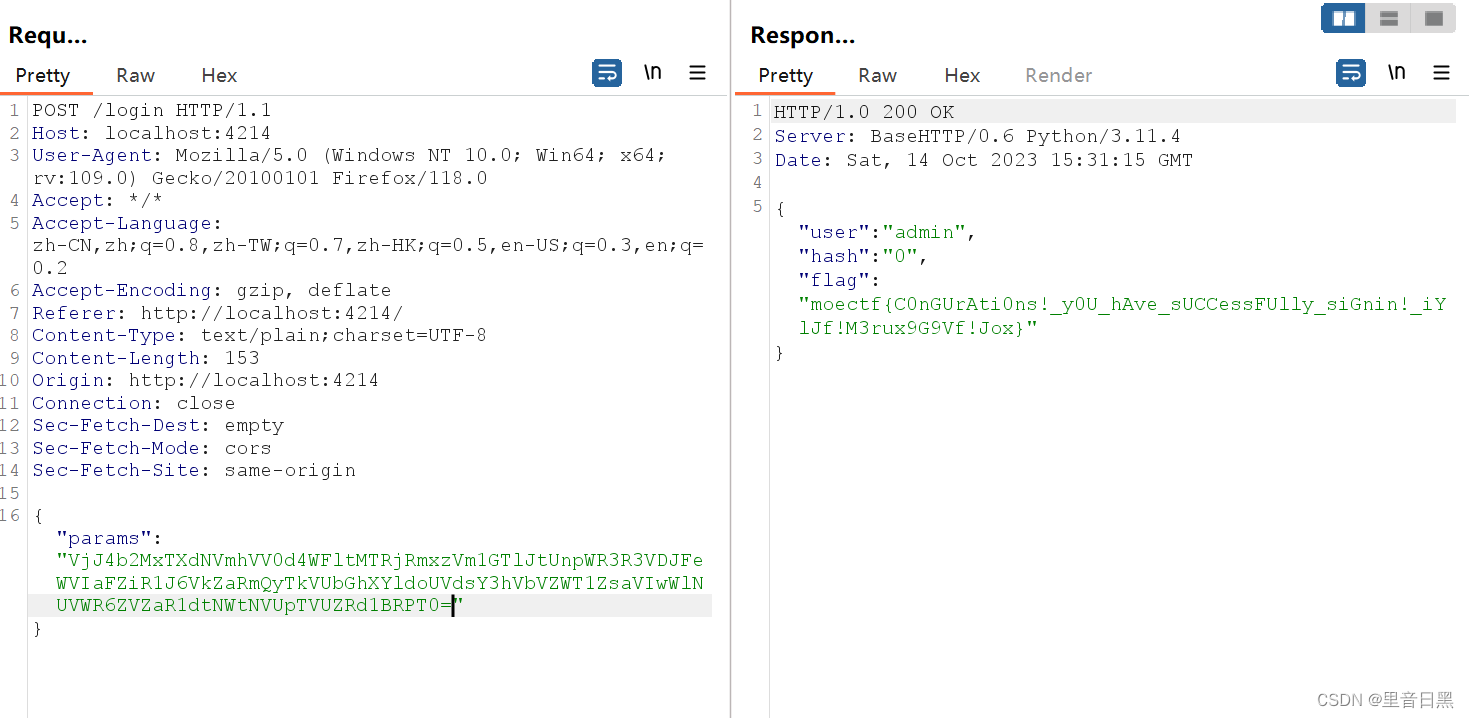
MoeCTF2023web
01http 打开题目环境 可以看到要求完成所有任务,这里用burp抓个包 按照要求修改可以得到flag moectf{basic_http_knowledge_HJbg427uFuznTqiJdtS1xhZNwpdsOnKU} 02 Web入门指北 直接找到结尾发现乱码,去解码 编码可以试试url编码和base64到16 这里用…...
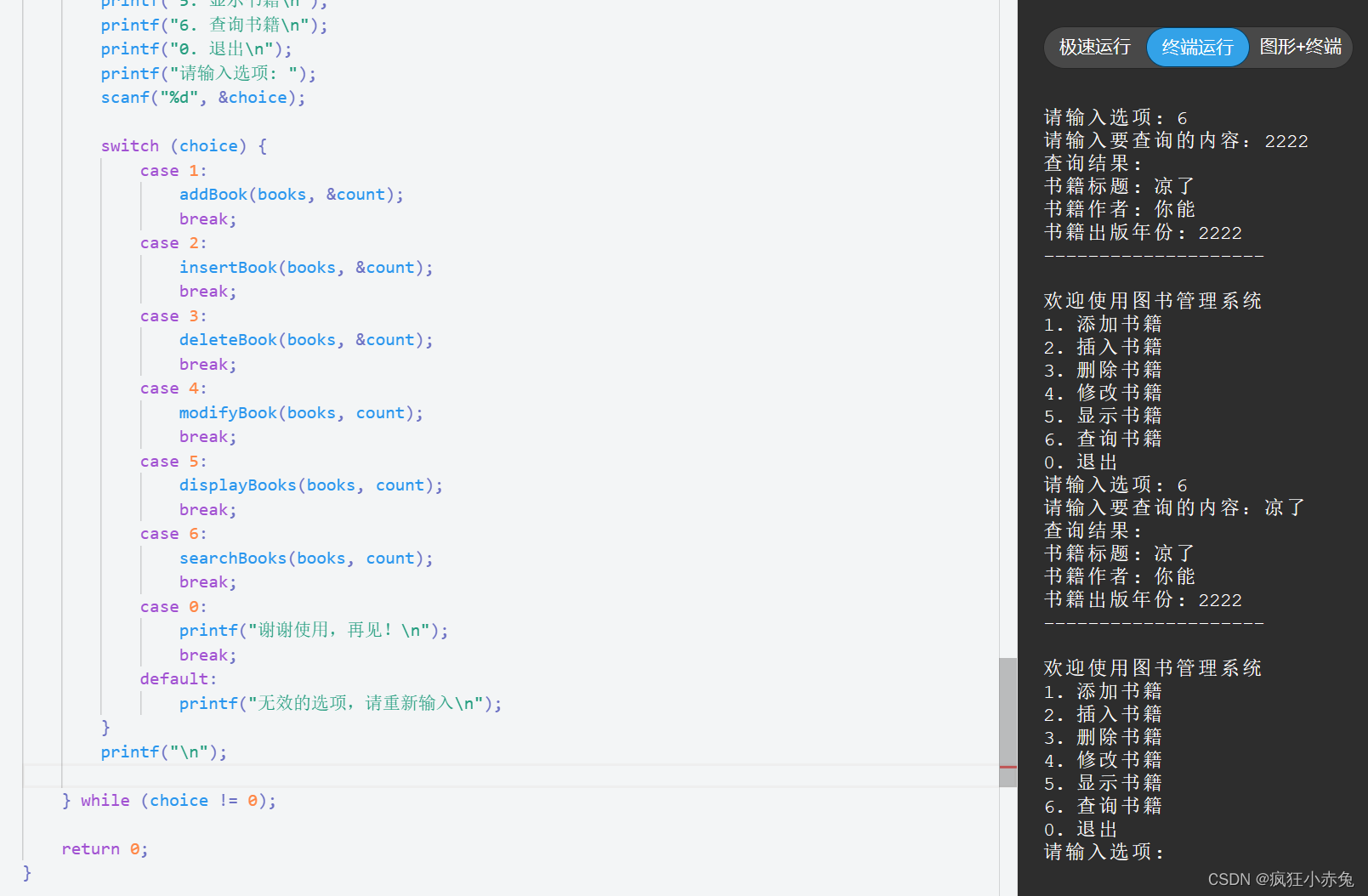
C语言编写简易图书管理系统
这篇文章介绍了一个基本的图书管理系统的实现,它允许用户添加、插入、删除、修改、显示和查询图书的功能。该系统通过使用二进制文件将图书信息保存到磁盘,并且在程序启动时能够加载已保存的图书信息。 介绍 在计算机科学中,图书管理系统是…...
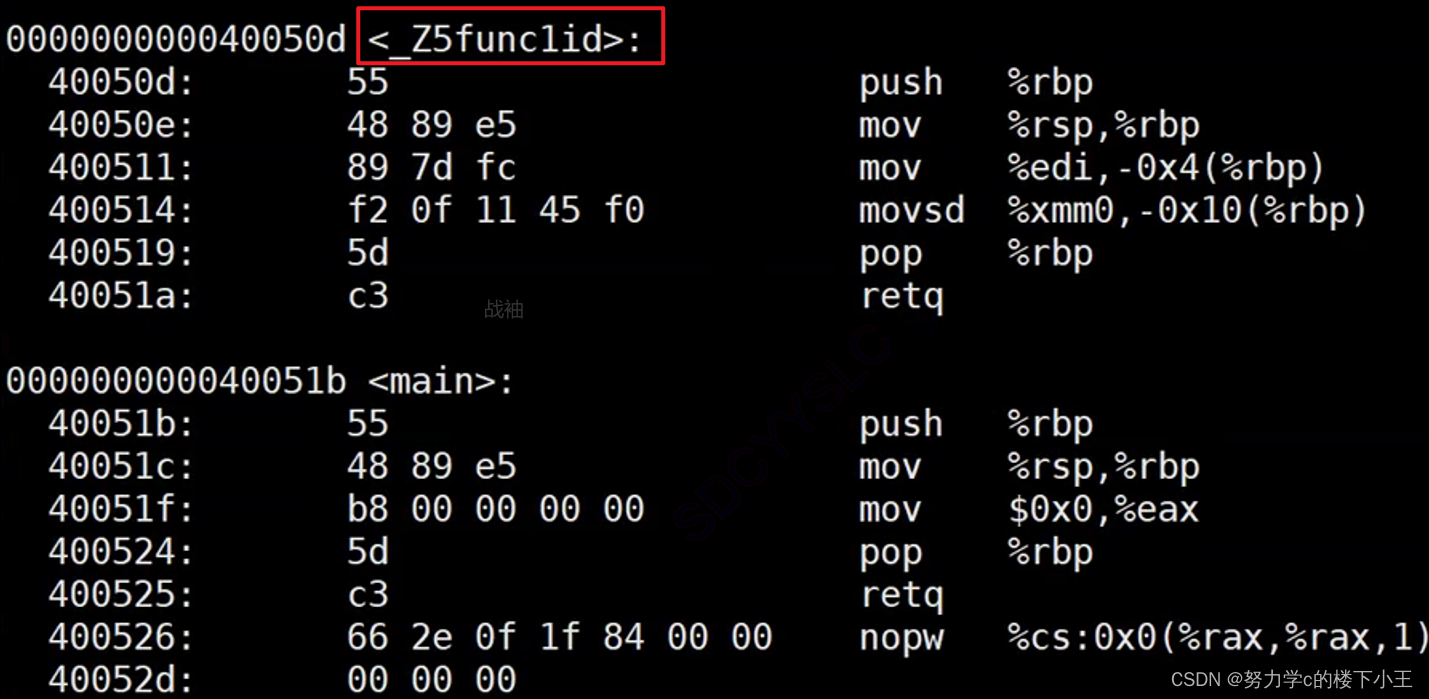
C++入门 第一篇(C++关键字, 命名空间,C++输入输出)
目录 1. C关键字 2. 命名空间 2.1 命名空间定义 2.2命名空间的使用 命名空间的使用有三种方式: 1.加命名空间名称及作用域限定符 2.使用using将命名空间中某个成员引入 3.使用using namespace 命名空间名称 引入 3. C输入&输出 4.缺省函数 4.1 缺省参…...

python股票波动性分析
一、简介 我们都经历过这样的情况——盯着股票图表,试图理解那些疯狂的价格上涨,或者只是想知道为什么突然平静。在这些波动中,有一个一致的因素常常脱颖而出:波动性。了解波动性为衡量任何特定点的市场情绪和情绪提供了一个视角。通过剖析波动性的细微差别,我们不仅可以更…...

53 打家劫舍
打家劫舍 题解1 DP1题解2 DP2 !经典DP! 你是一个专业的小偷,计划偷窃沿街的房屋。每间房内都藏有一定的现金,影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统,如果 两间相邻的房屋在同一晚上被小偷闯入…...
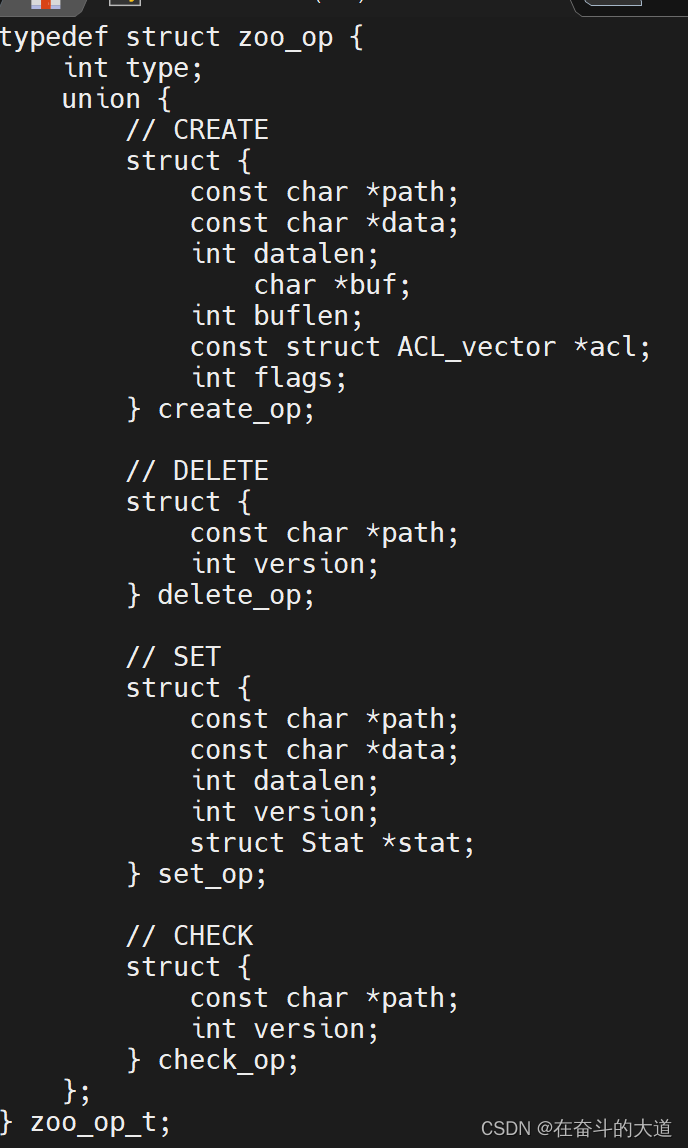
CentOS 7 基于C 连接ZooKeeper 客户端
前提条件:CentOS 7 编译ZooKeeper 客户端,请参考:CentOS 7 编译ZooKeeper 客户端 1、Docker 安装ZooKeeper # docker 获取zookeeper 最新版本 docker pull zookeeper# docker 容器包含镜像查看 docker iamges# 准备zookeeper 镜像文件挂载对…...

2023-2024-1 for循环-1(15-38)
7-15 输出闰年 输出21世纪中截止某个年份以来的所有闰年年份。注意:闰年的判别条件是该年年份能被4整除但不能被100整除、或者能被400整除。 输入格式: 输入在一行中给出21世纪的某个截止年份。 输出格式: 逐行输出满足条件的所有闰年年份,即每个年…...
初级问题 程序中的变量是指什么?中级问题 把若干个数据沿直线排列起来的数据结构叫作什么?高级问题 栈和队列的区别是什么?
目录 1.深刻主题 2.描写复杂人物 初级问题 程序中的变量是指什么? 中级问题 把若干个数据沿直线排列起来的数据结构叫作什么? 高级问题 栈和队列的区别是什么? 计算机图形学(有效边表算法) 介绍一下计算机图形学…...

clickhouse数据库简介,列式存储
clickhouse数据库简介 1、关于列存储 所说的行式存储和列式存储,指的是底层的存储形式,数据在磁盘上的真实存储,至于暴漏在上层的用户的使用是没有区别的,看到的都是一行一行的表格。 idnameuser_id1闪光10266032轨道物流10265…...

flask 发送ajax
前端 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><title>Title</title> </head> <body> <script src"https://cdn.lyshark.com/javascript/jquery/3.5.1/jquery.min.js"…...

Android Gradle 命令打包AAR
平台 Android Archive (AAR) 文件是一种特定于Android的存档文件格式,用于将Android库和资源打包成单个可重用的单元。AAR文件通常用于共享和分发Android库,以便其他Android应用项目可以轻松引用和使用这些库。 AAR文件是一种便捷的方式,用于…...
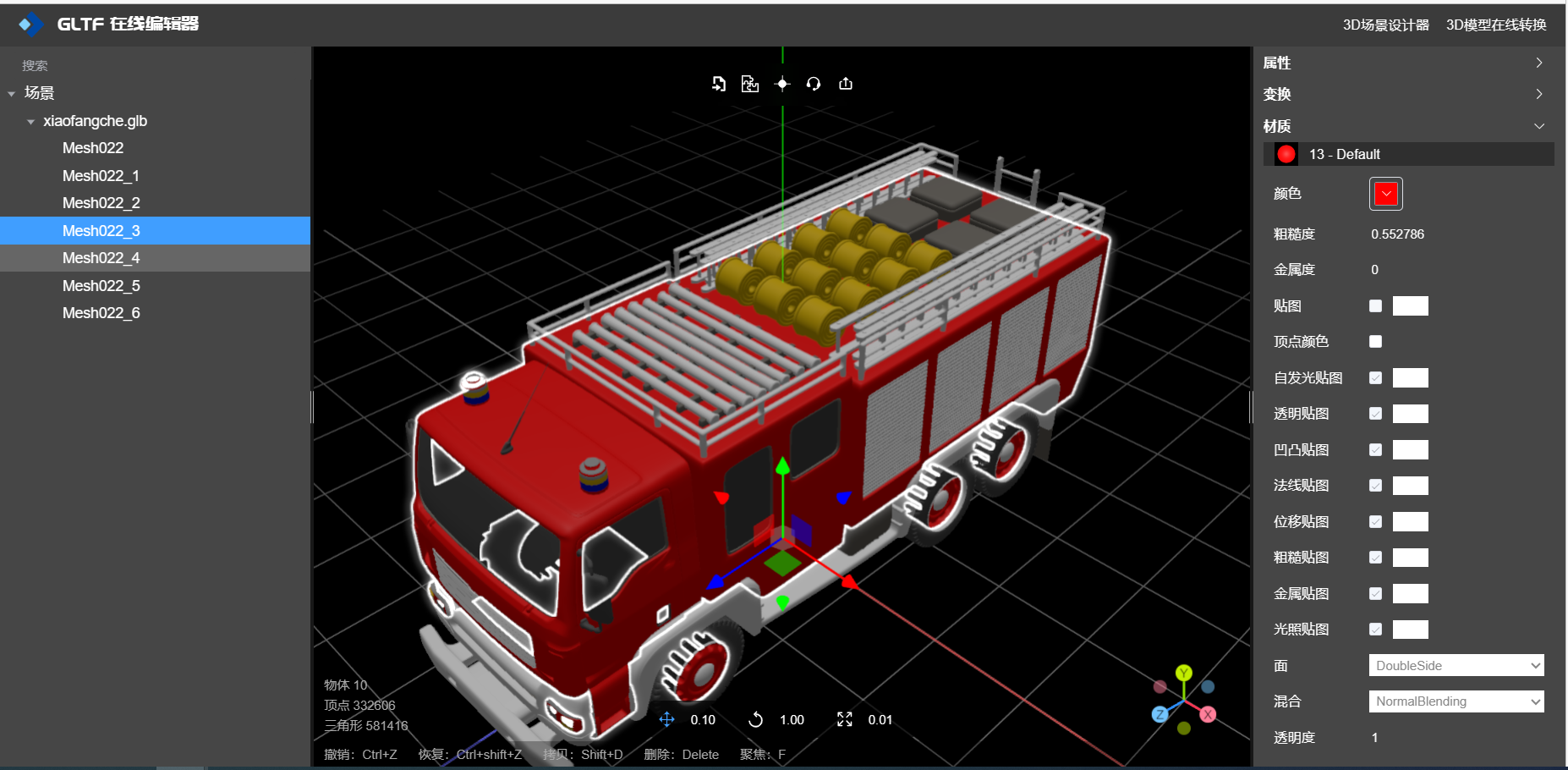
如何导出带有材质的GLB模型?
1、为什么要使用 GLB 模型? GLB格式(GLTF Binary)是一种用于存储和传输3D模型及相关数据的文件格式,具有以下优点和作用: 统一性:GLB是一种开放标准的3D文件格式,由Khronos Group制定和维护。它融合了GL…...

C/C++面试常见知识点
目录 C/C语言C内存分区malloc/free与new/delete的区别联合体联合体大小的计算 结构体对齐为什么需要结构体内存对齐 结构体与联合体的区别左值引用与右值引用指针和引用的区别迭代器失效static关键字在C语言的作用进程地址空间的分布内联函数 三大特性构造函数不能是虚函数析构…...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...
中的KV缓存压缩与动态稀疏注意力机制设计)
大语言模型(LLM)中的KV缓存压缩与动态稀疏注意力机制设计
随着大语言模型(LLM)参数规模的增长,推理阶段的内存占用和计算复杂度成为核心挑战。传统注意力机制的计算复杂度随序列长度呈二次方增长,而KV缓存的内存消耗可能高达数十GB(例如Llama2-7B处理100K token时需50GB内存&a…...

在Ubuntu24上采用Wine打开SourceInsight
1. 安装wine sudo apt install wine 2. 安装32位库支持,SourceInsight是32位程序 sudo dpkg --add-architecture i386 sudo apt update sudo apt install wine32:i386 3. 验证安装 wine --version 4. 安装必要的字体和库(解决显示问题) sudo apt install fonts-wqy…...

Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析
Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析 一、第一轮提问(基础概念问题) 1. 请解释Spring框架的核心容器是什么?它在Spring中起到什么作用? Spring框架的核心容器是IoC容器&#…...

动态 Web 开发技术入门篇
一、HTTP 协议核心 1.1 HTTP 基础 协议全称 :HyperText Transfer Protocol(超文本传输协议) 默认端口 :HTTP 使用 80 端口,HTTPS 使用 443 端口。 请求方法 : GET :用于获取资源,…...
混合(Blending))
C++.OpenGL (20/64)混合(Blending)
混合(Blending) 透明效果核心原理 #mermaid-svg-SWG0UzVfJms7Sm3e {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-icon{fill:#552222;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-text{fill…...

基于PHP的连锁酒店管理系统
有需要请加文章底部Q哦 可远程调试 基于PHP的连锁酒店管理系统 一 介绍 连锁酒店管理系统基于原生PHP开发,数据库mysql,前端bootstrap。系统角色分为用户和管理员。 技术栈 phpmysqlbootstrapphpstudyvscode 二 功能 用户 1 注册/登录/注销 2 个人中…...

十九、【用户管理与权限 - 篇一】后端基础:用户列表与角色模型的初步构建
【用户管理与权限 - 篇一】后端基础:用户列表与角色模型的初步构建 前言准备工作第一部分:回顾 Django 内置的 `User` 模型第二部分:设计并创建 `Role` 和 `UserProfile` 模型第三部分:创建 Serializers第四部分:创建 ViewSets第五部分:注册 API 路由第六部分:后端初步测…...
