【算法学习】-【滑动窗口】-【找到字符串中所有字母异位词】
LeetCode原题链接:438. 找到字符串中所有字母异位词
下面是题目描述:
给定两个字符串 s 和 p,找到 s 中所有 p 的 异位词 的子串,返回这些子串的起始索引。不考虑答案输出的顺序。
异位词 指由相同字母重排列形成的字符串(包括相同的字符串)。
示例 1:
输入: s = “cbaebabacd”, p = “abc”
输出: [0,6]
解释:
起始索引等于 0 的子串是 “cba”, 它是 “abc” 的异位词。
起始索引等于 6 的子串是 “bac”, 它是 “abc” 的异位词。
示例 2:
输入: s = “abab”, p = “ab”
输出: [0,1,2]
解释:
起始索引等于 0 的子串是 “ab”, 它是 “ab” 的异位词。
起始索引等于 1 的子串是 “ba”, 它是 “ab” 的异位词。
起始索引等于 2 的子串是 “ab”, 它是 “ab” 的异位词。
1、解题思路
前言:如果有第一次学习滑动窗口算法的朋友,可以先阅读一下笔者关于滑动窗口算法的第一篇文章:【算法学习】-【滑动窗口】-【长度最小的子数组】,那里对滑动窗口会有较详细的讲解,下面的解题思路中关于相关算法的步骤就仅进行简单的叙述啦。
由题目描述可得, 本题主要可分为以下两个步骤:
(1)判断一个字符串是否为另一个字符串的异位词
这里需要借助哈希表这个数据结构来进行判断,即将两个字符串中的字符分别放入两个哈希表中,然后对比这两个哈希表,若两个哈希表中的字符及字符个数都一样,则说明是异位词;否则不是。
(2)确定滑动窗口
相较于之前笔者有关滑动窗口算法的文章中的滑动窗口,这里的窗口大小是恒定的,即用于构成窗口大小的两个指针是 “共进退” 的。故此时直接照搬之前控制窗口移动的思路反而会使情况变得复杂。下面介绍一下算法的步骤:
- 先初始化两个哈希表,便于直接进行第一次判断
- 判断两个哈希表中的内容否相等,若相等,则记录索引(也就是构成窗口的前面的那个指针的值)
- 接着无论是否相等都需将字符串s对应的哈希表中的第一个字符删除(注意这里要先让数量
--,数量为0后才执行删除操作)而进行下一次枚举 - 删除后,向s对应的哈希表中插入新的字符,然后两个指针都向后移动一位,准备进行下一次的判断。循环执行上述过程。
2、具体代码
vector<int> findAnagrams(string s, string p){unordered_map<char, int> mapOfp;unordered_map<char, int> mapOfs;//初始化哈希表for (size_t i = 0; i < p.size(); i++){mapOfp[p[i]]++;mapOfs[s[i]]++;}vector<int> res;size_t cur = p.size();size_t begin = 0;while (cur <= s.size()){if (mapOfp == mapOfs){res.push_back(begin);}if( --mapOfs[s[begin]] == 0){mapOfs.erase(s[begin]);}begin++;mapOfs[s[cur++]]++;}if (mapOfp == mapOfs){res.push_back(begin);}return res;}
看完觉得有觉得帮助的话不妨点赞收藏鼓励一下,有疑问或看不懂的地方或有可优化的部分还恳请朋友们留个评论,多多指点,谢谢朋友们!🌹🌹🌹
相关文章:

【算法学习】-【滑动窗口】-【找到字符串中所有字母异位词】
LeetCode原题链接:438. 找到字符串中所有字母异位词 下面是题目描述: 给定两个字符串 s 和 p,找到 s 中所有 p 的 异位词 的子串,返回这些子串的起始索引。不考虑答案输出的顺序。 异位词 指由相同字母重排列形成的字符串&…...

利用python学习如何处理需要登录的网站
要处理需要登录的网站,你可以按照以下步骤进行学习: 了解网站的登录机制:登录机制通常有用户名密码登录、OAuth授权登录、Cookie登录等。了解目标网站使用的登录机制是学习处理的第一步。 使用Web抓取工具模拟登录:通过使用工具如…...

vue适配各个屏幕
1:不是响应式,只是用缩放来适配各个pc 2:使用中会出现由于 transform 属性导致的定位问题,具体的需要针对性的处理 App.vue <div id"app" ><div class"app-view" :style"{--scale:scale}"><…...

在conda创建的虚拟环境中安装jupyter以及使用
1. 进入你的虚拟环境 conda activate conda_env_name 2. 安装jupyter notebook conda install -y jupyter 3. 启动jupyter jupyter notebook 4. 将conda环境添加到jupyter的内核中 conda install ipykernel python -m ipykernel install --name conda_env_namepython -m…...

【Java 8的新特性】
引言 Java 8是Java编程语言的一个重要里程碑,它引入了许多令人兴奋的新特性和改进。这些新特性不仅使Java编程更加简洁和高效,还提供了更多的功能和灵活性。在本文中,我们将探讨Java 8的一些重要新特性,并展示它们是如何改变我们…...
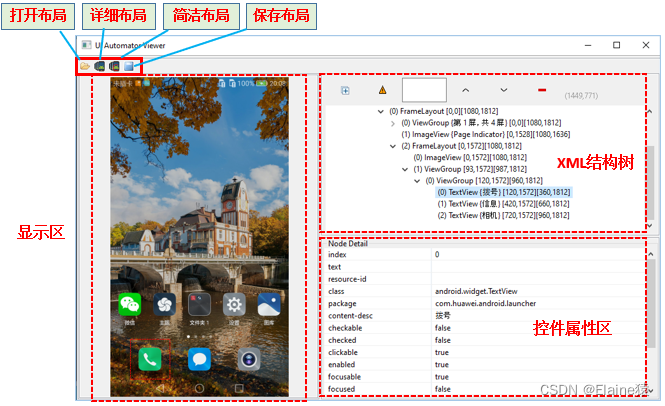
Android+Appium自动化测试环境搭建及实操
1、Appium简介1.1 Appium概念1.2 Appium工作原理 2、Appium Server环境搭建2.1 Java JDK2.1.1 下载JDK2.1.2 运行exe安装JDK,设置安装路径2.1.3 设置环境变量2.1.4 验证安装结果 2.2 Android SDK2.2.1 下载安装Android SDK安装包2.2.2 下载platform-tools࿰…...
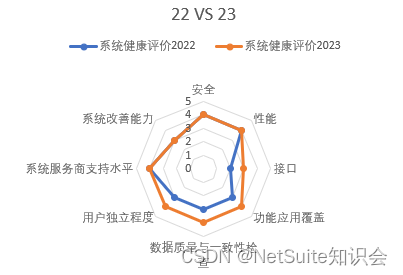
NetSuite ERP系统健康检查
这个题目来自最近的一个项目感受,“上线即停滞”。这是在中小型企业十分普遍的一个情况,一旦上线后,基本上信息化的建设就停止了。这是一个中小企业信息化的一个特点,因为其IT力量比较弱,所以在信息化的推动中缺乏话语…...
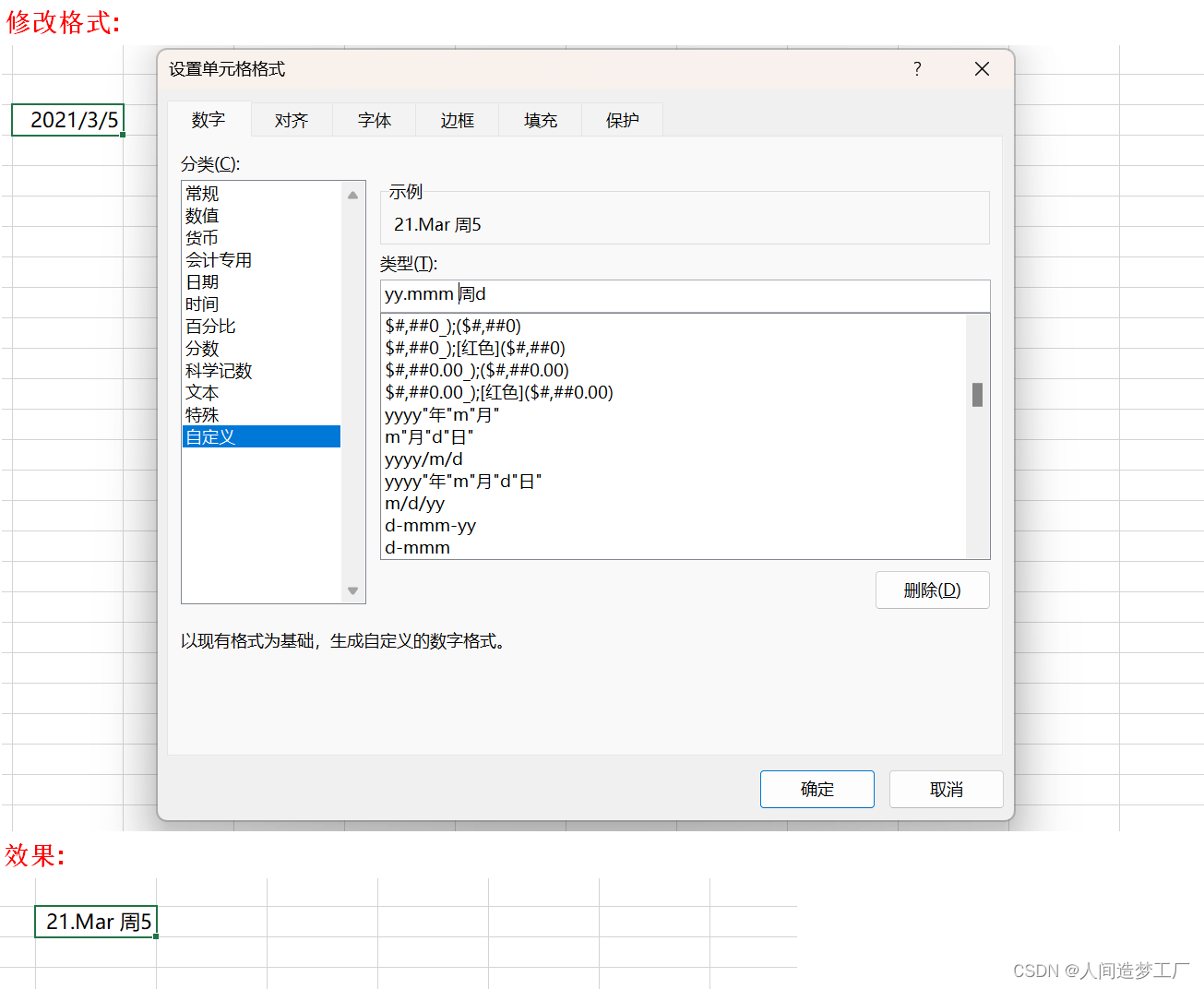
常用的数字格式代码
文章目录 数值占位符文本占位符 两类占位符: 数值占位符, 文本占位符. 数值占位符 有三种:0,#,? 0 是强制的占位符。 文本占位符 文本占位符只有一个: : 作用于文本的占位符,可以用英文引号" &quo…...
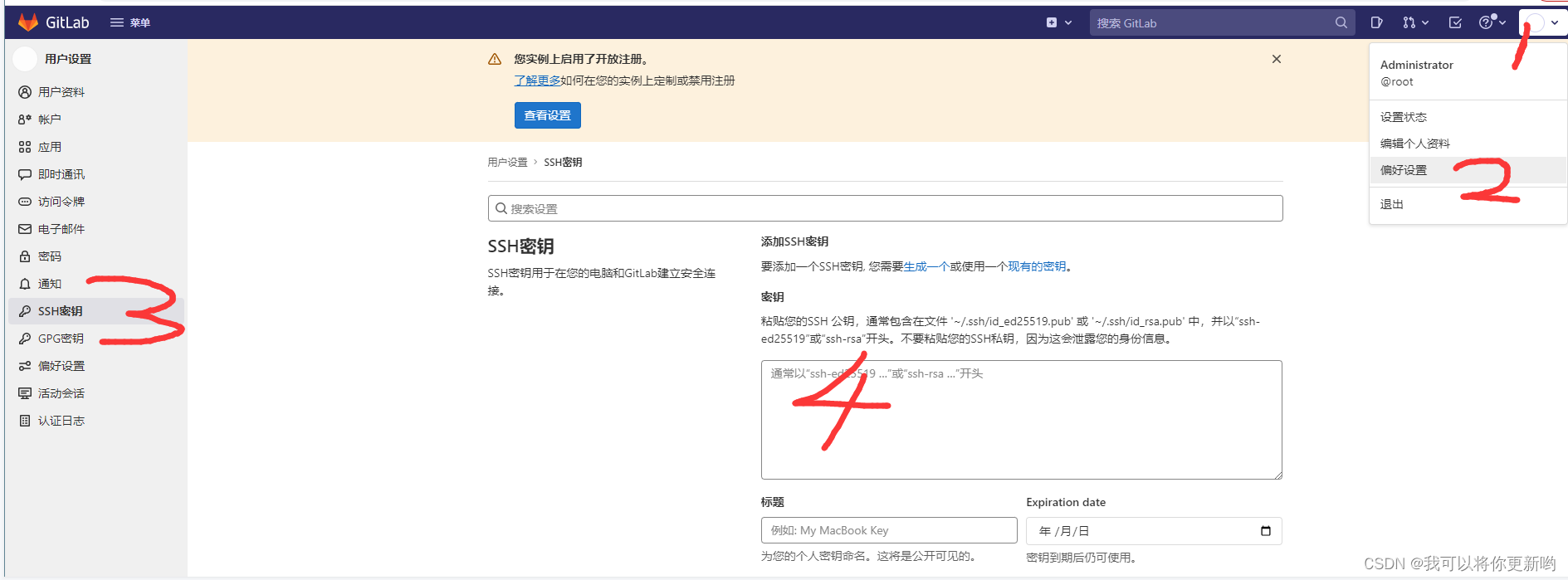
GitLab使用步骤
GitLab使用步骤 1 注册用户 1 访问:http://10.0.0.203/users/sign_up地址 2 填入注册信息,注册成功,需要管理员审核 3 用root登录,地址:http://10.0.0.203/users/sign_in账号:root密码:xxxx…...

基于MindSpore的llama微调在OpenI平台上运行
基于MindSpore的llama微调在OpenI平台上运行 克隆预训练模型 克隆chatglm-6b代码仓,下载分布式的模型文件 git lfs install git clone https://huggingface.co/openlm-research/open_llama_7b准备环境 安装Transformer pip install transformers执行转换脚本 …...
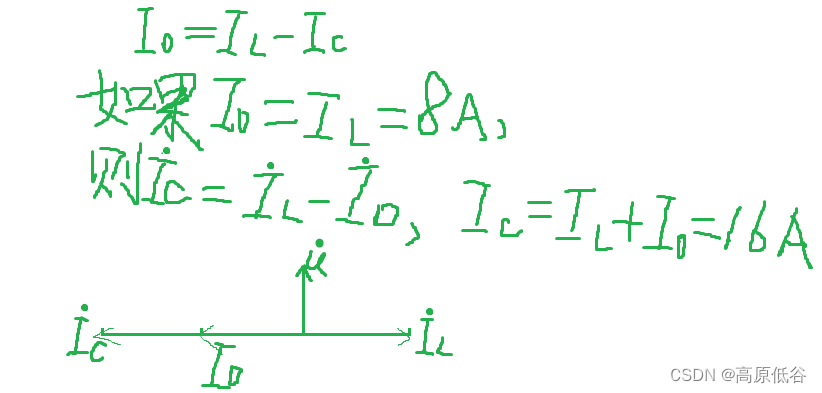
P34~36第八章相量法
8.1复数 复数可表示平面矢量、也可表示正弦量。特别是: 当复数表示正弦量的时候,此时复数称为相量。 8.2复数运算 复数除法也可看做乘法,乘法的几何意义是旋转(辐角相加)( e^x e^y e^xy),同时伸缩(模变…...
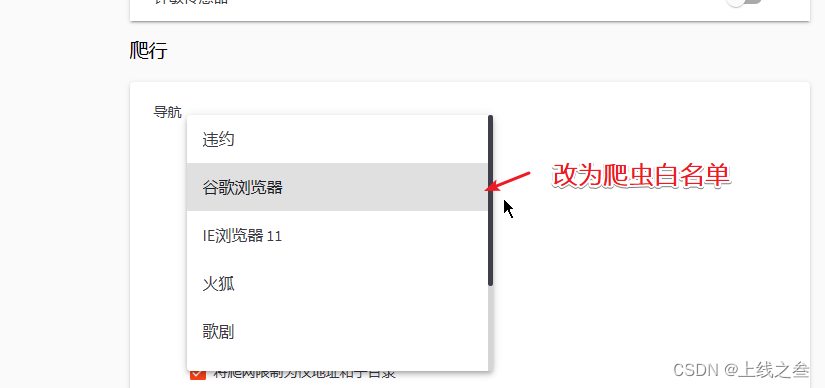
WAF绕过-漏洞发现之代理池指纹探针 47
工具 工具分为综合性的,有awvs,xray,单点的比如wpscan专门扫描wordpress的。而我们使用工具就可能会触发waf, 触发点 第一个就是扫描速度,太快了,可以通过演示,开代理池,白名单绕…...
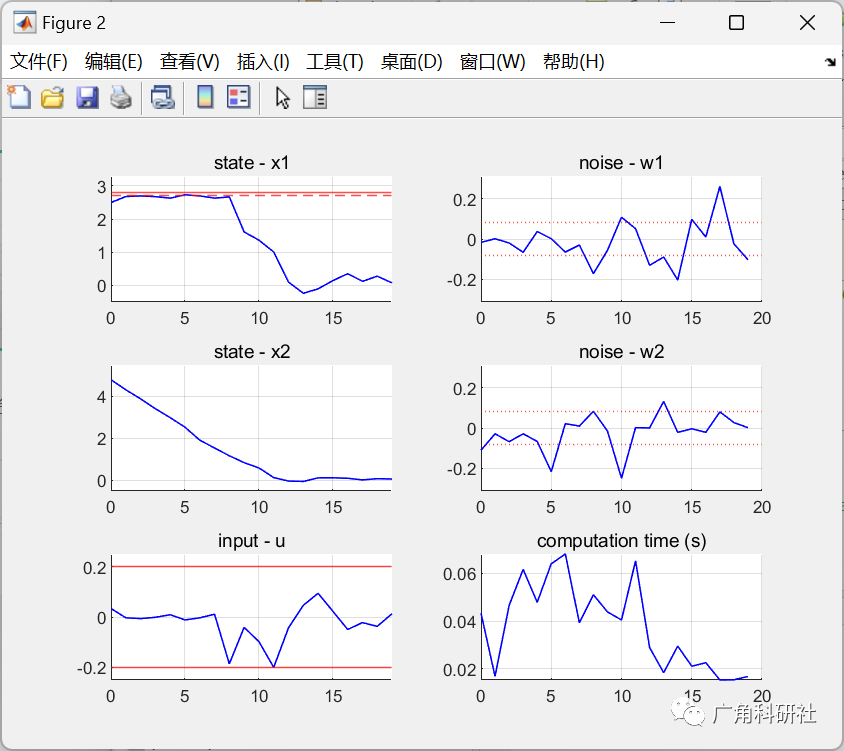
模型预测控制(MPC)中考虑约束中的不确定性(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...
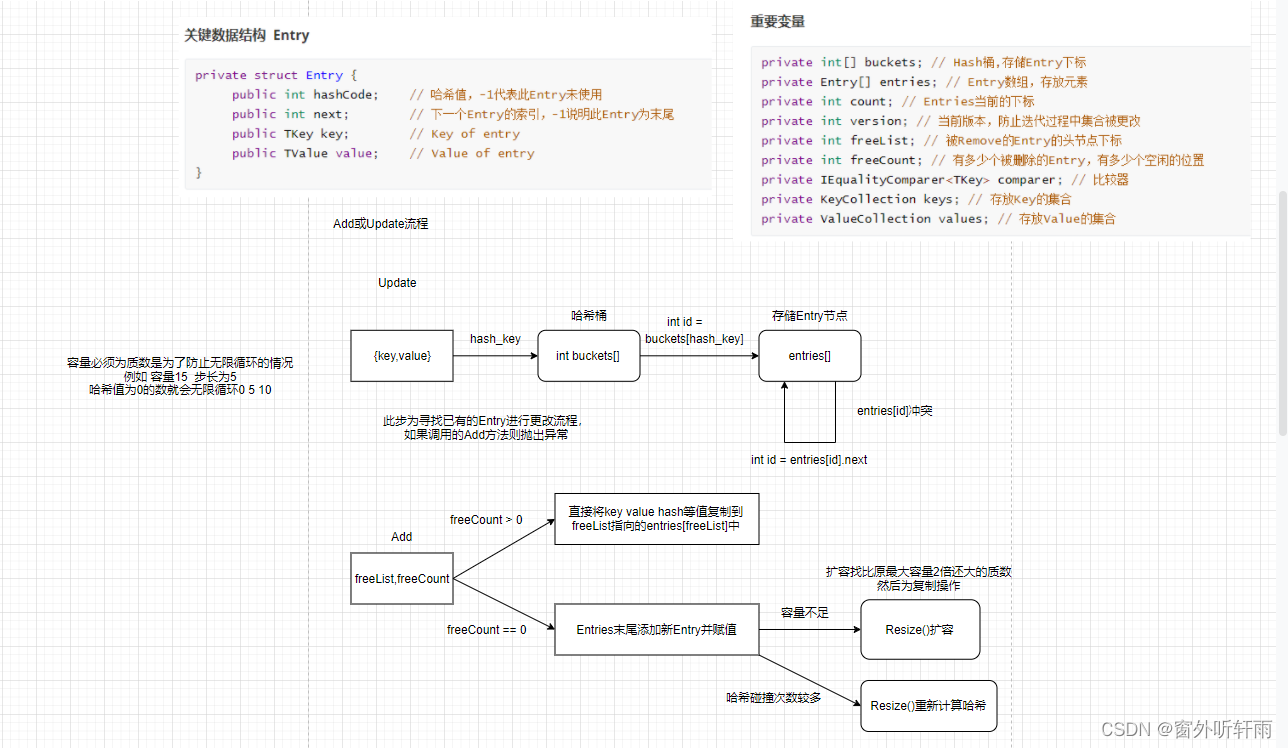
校招C#面试题整理—Unity客户端
前言 博客已经1年多没有更新了,这一年主要在实习并准备秋招和春招,目前已经上岸Unity客户端岗位,现将去年校招遇到的一些面试题的事后整理分享出来。答案是笔者自己整理的不一定保证准确,欢迎大家在评论区指出。 Unity客户端岗的…...

【数字IC设计】利用Design Compiler评估动态功耗
利用DC对RTL设计的动态功耗进行评估,主要可以分为以下步骤: 用vcs编译运行testbench,生成.saif文件(Switching Activity Interchange Format)在Design Compiler编译前,读入.saif文件Design Compiler编译完设计文件后,输出功耗报告 下面通过一个计数器的设计,来演示该过程…...

Docker Compose命令讲解+文件编写
docker compose的用处是对 Docker 容器集群的快速编排。(源码) 一个 Dockerfile 可以定义一个单独的应用容器。但我们经常碰到需要多个容器相互配合来完成某项任务的情况(如实现一个 Web 项目,需要服务器、数据库、redis等&#…...
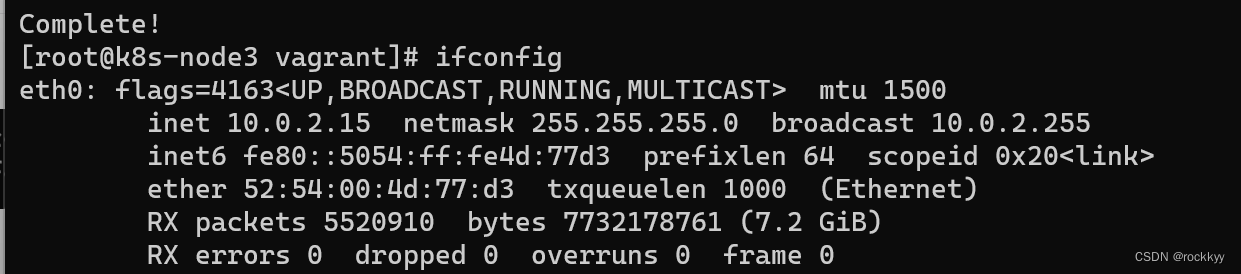
Linux bash: ipconfig: command not found解决方法
安装完centos7运行ifconfig命令发现找不到 安装相关工具 yum install net-tools.x86_64 无脑yes即可...
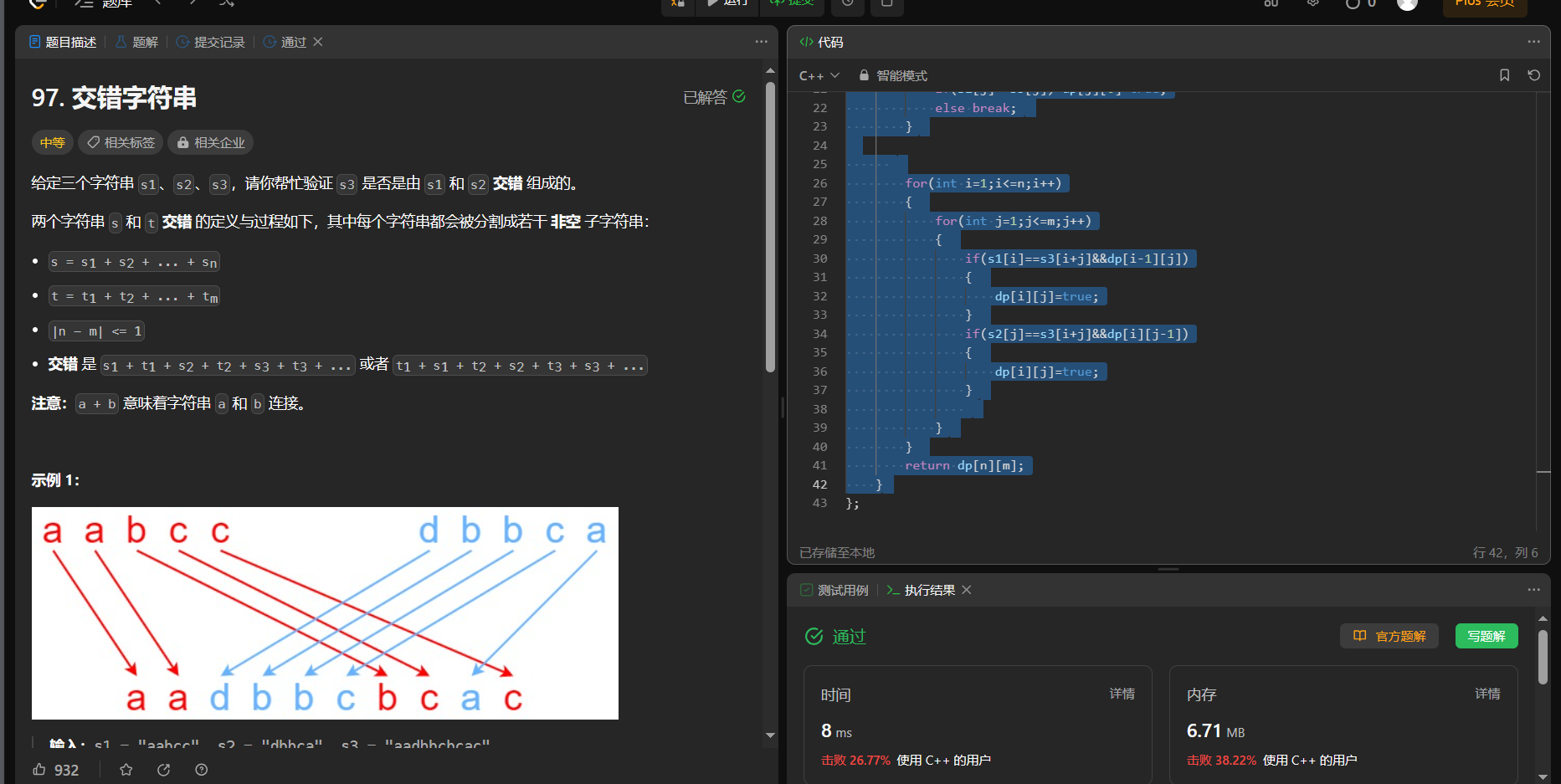
【面试算法——动态规划 21】正则表达式匹配(hard) 交错字符串
10. 正则表达式匹配 链接: 10. 正则表达式匹配 给你一个字符串 s 和一个字符规律 p,请你来实现一个支持 ‘.’ 和 ‘*’ 的正则表达式匹配。 ‘.’ 匹配任意单个字符 ‘*’ 匹配零个或多个前面的那一个元素 所谓匹配,是要涵盖 整个 字符串 s的…...

基于Python实现的神经网络分类MNIST数据集
神经网络分类MNIST数据集 目录 神经网络分类MNIST数据集 1 一 、问题背景 1 1.1 神经网络简介 1 前馈神经网络模型: 1 1.2 MINST 数据说明 4 1.3 TensorFlow基本概念 5 二 、实现说明 5 2.1 构建神经网络模型 5 为输入输出分配占位符 5 搭建分层的神经网络 6 处理预…...
设计模式之是简单工厂模式
分类 设计模式一般分为三大类:创建型模式、结构型模式、行为型模式。 创建型模式:用于创建对象,共五种,包括单例模式、简单工厂模式、工厂方法模式、抽象工厂模式、建造者模式、原型模式。结构型模式:用于处理类或对…...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...
` 方法)
深入浅出:JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出:JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中,随机数的生成看似简单,却隐藏着许多玄机。无论是生成密码、加密密钥,还是创建安全令牌,随机数的质量直接关系到系统的安全性。Jav…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

Go 语言并发编程基础:无缓冲与有缓冲通道
在上一章节中,我们了解了 Channel 的基本用法。本章将重点分析 Go 中通道的两种类型 —— 无缓冲通道与有缓冲通道,它们在并发编程中各具特点和应用场景。 一、通道的基本分类 类型定义形式特点无缓冲通道make(chan T)发送和接收都必须准备好࿰…...

scikit-learn机器学习
# 同时添加如下代码, 这样每次环境(kernel)启动的时候只要运行下方代码即可: # Also add the following code, # so that every time the environment (kernel) starts, # just run the following code: import sys sys.path.append(/home/aistudio/external-libraries)机…...

Xela矩阵三轴触觉传感器的工作原理解析与应用场景
Xela矩阵三轴触觉传感器通过先进技术模拟人类触觉感知,帮助设备实现精确的力测量与位移监测。其核心功能基于磁性三维力测量与空间位移测量,能够捕捉多维触觉信息。该传感器的设计不仅提升了触觉感知的精度,还为机器人、医疗设备和制造业的智…...
