动态规划算法(3)--0-1背包、石子合并、数字三角形
目录
一、0-1背包
1、概述
2、暴力枚举法
3、动态规划
二、石子合并问题
1、概述
2、动态规划
3、环形石子怎么办?
三、数字三角形问题
1、概述
2、递归
3、线性规划
四、租用游艇问题
一、0-1背包
1、概述
0-1背包:给定多种物品和一个固定重量W的背包,每种物品有一个固定的重量,价值
,现在要将物品装入背包,每种物品至多装入一个,使总重量不超过W,且总价值最大。
约束条件和优化目标如下:

2、暴力枚举法
暴力枚举法也是使用递归的方式,假设对前i个物品分析,总重量为c,当前总价值为P。那么存在递归条件:
另外当重量小于0时,总价值为-∞(代码中可以用-999替代),物品个数小于等于0,总价值为0。
暴力枚举法依赖递归方式,没有减少子问题个数,所以根据递归树计算,复杂度为。
伪代码如下:

代码实例:
//暴力枚举public static int violate_knapsack(int weight,int i,int weights[],int values[]){if (weight<0){return -9999; }if (i<=0) { return 0;}int p1=violate_knapsack(weight-weights[i],i-1,weights,values); //选中i物品int p2=violate_knapsack(weight,i-1,weights,values); //不选i物品int p=p1+values[i]>p2?p1+values[i]:p2; return p;}3、动态规划
动态规划方法通过建立备忘录的方式,前i个物品,总重量为j的时刻永远依赖于前面的子结构。M数组为加入前i个物品后,总重量为j时的总价值,Rec数组表示是否有物品添加,若添加则为1,不添加则为0。
原理:
参数:count代表总类别个数,weight代表背包重量,weights为物品重量,values为物品价值,name为物品名称。
(1)首先,M数组0行0列均为初值0,注意:行为重量,列为种类个数。
(2)按每行逐个值来填写M和Rec。如:前i个物品,总重量为j的情况下,即求M[i][j]时,如果该物品重量小于背包重量且在前i-1个物品,总重量为(j-当前物品重量)时的总重量+当前物品价值的总价值,大于前i-1个物品,总重量为j时的总价值时M填写较大的总价值,Rec=1。条件写为:
(3)由于调用j-当前物品重量时有可能为负数,所以保证最小值为0,设为minor。
(4)如果不满足(2)条件,则M[i][j]填上一行同列的M[i-1][j]值,即不选这个物品(索引为i-1)的总价值。Rec为0。
(5)最优解追寻:Rec数组倒序查找i取最大值,逐次减1,判断条件如果Rec数组为1,则从总重量weight中减少weights[i-1],输出name[i-1]物品,直到i取1。
//0-1背包问题
import java.util.ArrayList;
public class backage {public static void main(String []args){int values[]={24,2,9,10,9};int weights[]={10,3,4,5,4};int count=5;int weight=13;int M[][]=new int [count+1][weight+1];int Rec[][]=new int [count+1][weight+1];String name[]={"beer","cocacola","cookie","bread","milk"};//暴力求解System.out.println(violate_knapsack(weight,count-1,weights,values)); //建立M数组,Rec数组 knapsack(count,weight,M,Rec,weights,values);//M数组for(int i=0;i<count+1;i++){for(int j=0;j<weight+1;j++){System.out.print(M[i][j]+"\t");}System.out.println("");}//Rec数组for(int i=0;i<count+1;i++){for(int j=0;j<weight+1;j++){System.out.print(Rec[i][j]+"\t");}System.out.println("");}//输出最优解Print(count,weight,Rec,name,weights);} //动态规划public static void knapsack(int count,int weight,int M[][],int Rec[][],int weights[],int values[]){for(int i=0;i<count+1;i++) //0行0列没有值参与M[i][0]=0;for(int j=0;j<weight+1;j++)M[0][j]=0;for(int i=1;i<count+1;i++) //第一行的表示加入第一个物品,但是第一个物品在索引0处{for(int j=1;j<weight+1;j++){int minor; //minor的设计是防止j-weights出现小于0,有可能背包重量小于上一行物品的重量,从而小于背包质量,小于背包质量默认为0if(j-weights[i-1]<0)minor=0;elseminor=j-weights[i-1];if((weights[i-1]<=j) & (values[i-1]+M[i-1][minor]>M[i-1][j])) //如果可以替换,M替换为新值,Rec更新为1{M[i][j]=values[i-1]+M[i-1][minor];Rec[i][j]=1;}else{M[i][j]=M[i-1][j]; //不能修改时,M用上一行同列值替换,Rec更新为0Rec[i][j]=0;}}}}//输出最优解public static void Print(int count,int weight,int Rec[][],String name[],int weights[]){for(int i=count;i>0;i--){if(Rec[i][weight]==1){System.out.println(name[i-1]);weight=weight-weights[i-1];}}}M数组和Rec数组的写法:

二、石子合并问题
1、概述
现在有n堆石子排成一排,要求将石子有次序地合并成一堆,规定每次只能选相邻的两堆石子合并成新的一堆,并将新的一堆石子数记为该次合并的得分,设计一个算法将n堆石子合并成一堆的最小得分和最大得分。
类比矩阵连乘问题求解,利用动态规划,设计m和s数组,最大值为m[1][n]。
2、动态规划
动态规划转移方程(最小值):
动态规划转移方程(最大值):
3、环形石子怎么办?
如果题目要求石子堆围成一圈,其他要求不变,我们可以考虑将数组变为一个重复数组,由环形变为线性。如{1,2,3}则变为{1,2,3,1,2,3},n=2*n,然后考虑(j-i)>=arr_length时才满足原来的最多三个石子堆合并的问题。
动态规划转移方程相同,只是多了一个退出循环的条件,同样的生成m数组,假设石子堆为{4,4,5,9},当前生成最小值m数组应该为下图示例:

可以看到原先的m[1][n]为最小值,现在应该讨论,也就是四个数的最小值。
代码示例:
//石子合并问题
public class stonemerge {public static void main(String[] args){int arr[]={4,4,5,9};int n=arr.length;int m[][]=new int[n+1][n+1]; int m_[][]=new int[n*2+1][n*2+1];int s[][]=new int[n+1][n+1]; minserge(arr,m_);System.out.println(trackmin(arr, m_));maxserge(arr, m_);System.out.println(trackmax(arr,m_));}//最小合并m数组 public static void minserge(int arr_[],int m[][]){int n=arr_.length*2;int arr[]=new int[n];add_arr(arr,arr_);for(int i=1;i<n;i++)m[i][i]=0;for (int r = 2; r <=n; r++) {for (int i = 1; i <= n - r + 1; i++) { int j = i + r - 1;if((j-i)>=arr_.length)break; m[i][j] = m[i + 1][j] + sum(i,j,arr); for (int k = i + 1; k < j; k++){int t = m[i][k] + m[k + 1][j] + sum(i,j,arr);if (t < m[i][j]) m[i][j] = t;}}}}//最大合并m数组public static void maxserge(int arr_[],int m[][]){int n=arr_.length*2;int arr[]=new int[n];add_arr(arr,arr_);for(int i=1;i<n;i++)m[i][i]=0;for (int r = 2; r <=n; r++) {for (int i = 1; i <= n - r + 1; i++) { int j = i + r - 1;if((j-i)>=arr_.length)break; m[i][j] = m[i + 1][j] + sum(i,j,arr); for (int k = i + 1; k < j; k++){int t = m[i][k] + m[k + 1][j] + sum(i,j,arr);if (t > m[i][j]) m[i][j] = t;}}}}//合并代价public static int sum(int i,int j, int arr[]){int tot=0;for(int m=i-1;m<=j-1;m++)tot+=arr[m];return tot;}//环形转线性数组生成public static void add_arr(int arr[],int arr_[]){for(int i=0;i<arr.length;i++){if(i<arr_.length)arr[i]=arr_[i];elsearr[i]=arr_[i-arr_.length];}}//最小值public static int trackmin(int arr[],int m[][]){int n=arr.length;int min=m[1][n];for(int i=2;i<=n;i++){if(m[i][n+i-1]<min)min=m[i][n+i-1];}return min;}//最大值public static int trackmax(int arr[],int m[][]){int n=arr.length;int max=m[1][n];for(int i=2;i<=n;i++){if(m[i][n+i-1]>max)max=m[i][n+i-1];}return max;}
}三、数字三角形问题
1、概述
给定一个由n行数字组成的数字三角形,设计算法,计算从三角形的顶至底的一条路径,每次必须下降一层,使该路径经过数字总和最大,如下图路线7-3-8-7-5,总和30。

2、递归
递归条件:
当x==n-1时为最底层数字,返回该数字。
//递归方法
public static int test(int x,int y,int nums[][]) {int n=nums.length;if(x == n-1) {return nums[x][y];}return (nums[x][y] + (test(x+1,y,nums) >= test(x+1,y+1,nums) ? test(x+1,y,nums) : test(x+1,y+1,nums)));}3、线性规划
状态转移方程与递归条件一样,只不过从倒数第二层向上叠加(参数i),每层的值改变为当前层到底层的最大值,变量k遍历某一层的每个数字,计算到底层的最大值并保存。
//动态规划
public static int max(int nums[][])
{for(int i=nums.length-2;i>=0;i--){int j=nums[i].length;for(int k=0;k<j;k++){nums[i][k]+=(nums[i+1][k]>=nums[i+1][k+1]?nums[i+1][k]:nums[i+1][k+1]);}}return nums[0][0];
}四、租用游艇问题
游艇出租站租用游艇,并在下游的任何一个游艇出租站归还游艇,游艇出租站i到游艇出租站j之间的租金为r(i,j)(1<=i<j<=n),设计算法,计算出游艇出租站1到游艇出租站n的最少租金。
输入的数字,第一行代表1到2的距离和1到3的距离,第二行代表2到3的距离。
//租用游艇问题
public class rentyacht {public static void main(String [] args){int cost[][]={{5,15},{7}};int n=cost.length;System.out.println(rentmin(cost,n));} public static int rentmin(int[][] cost, int n) {int[][] best = new int[n + 1][n + 1];for(int i = n - 1; i >= 1; i--) {best[i][n] = cost[i-1][n-1];for(int j = n - 1; j > i; j--) {best[i][n] = cost[i-1][j-1] + best[j][n]<best[i][n]?cost[i-1][j-1] + best[j][n]:best[i][n];}}return best[1][n];}
}
相关文章:
动态规划算法(3)--0-1背包、石子合并、数字三角形
目录 一、0-1背包 1、概述 2、暴力枚举法 3、动态规划 二、石子合并问题 1、概述 2、动态规划 3、环形石子怎么办? 三、数字三角形问题 1、概述 2、递归 3、线性规划 四、租用游艇问题 一、0-1背包 1、概述 0-1背包:给定多种物品和一个固定…...
Linux C/C++ 嗅探数据包并显示流量统计信息
嗅探数据包并显示流量统计信息是网络分析中的一种重要技术,常用于网络故障诊断、网络安全监控等方面。具体来说,嗅探器是一种可以捕获网络上传输的数据包,并将其展示给分析人员的软件工具。在嗅探器中,使用pcap库是一种常见的方法…...

Vitis导入自制IP导致无法构建Platform
怎么还有这种问题( 解决Vitis导入自制IP导致无法构建Platform – TaterLi 个人博客 Vitis报错:fatal error: xxx.h: No such file or directory._ly2lj的博客-CSDN博客 在指定位置黏入以上代码即可: INCLUDEFILES$(wildcard *.h) LIBSOUR…...

SQLAlchemy 使用封装实例
类封装 database.py #! /usr/bin/env python # -*- coding: utf-8 -*-import sys import json import logging from datetime import datetimefrom core.utils import classlock, parse_bool from core.config import (MYSQL_HOST,MYSQL_PORT,MYSQL_USER,MYSQL_PASS,MYSQL_DA…...
Android Framework通信:Binder
文章目录 前言一、Linux传统跨进程通信原理二、Android Binder跨进程通信原理1、动态内核可加载模块2、内存映射3、Binder IPC 实现原理 三、Android Binder IPC 通信模型1、Client/Server/ServiceManager/驱动Binder与路由器之间的角色关系 2、Binder通信过程3、Binder通信中的…...

如何用精准测试来搞垮团队?
测试行业每年会冒出来一些新鲜词:混沌工程、精准测试、AI测试…… 这些新概念、新技术让我们感到很焦虑,逼着自己去学习和了解这些新玩意,担心哪一天被淘汰掉。 以至于给我这样的错觉,当「回归测试」、「精准测试」这两个词摆在一…...
暴力递归转动态规划(十)
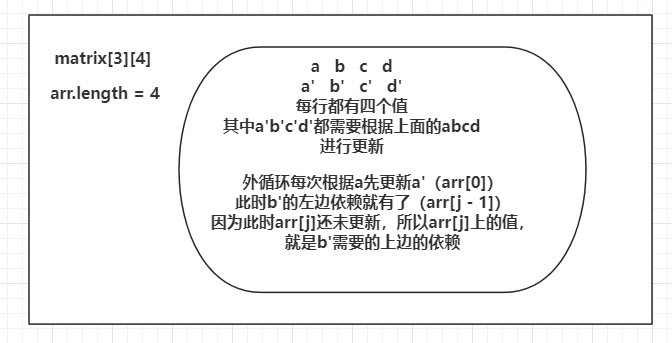
题目 给定一个二维数组matrix[][],一个人必须从左上角出发,最终到达右下角,沿途只可以向下或者向右走,沿途的数字都累加就是距离累加和。返回最小距离累加和。 这道题中会采用压缩数组的算法来进行优化 暴力递归 暴力递归方法的整…...

深度学习-房价预测案例
1. 实现几个函数方便下载数据 import hashlib import os import tarfile import zipfile import requests#save DATA_HUB dict() DATA_URL http://d2l-data.s3-accelerate.amazonaws.com/def download(name, cache_diros.path.join(.., data)): #save"""下载…...

【26】c++设计模式——>命令模式
c命令模式 C的命令模式是一种行为模式,通过将请求封装成对象,以实现请求发送者和接受者的解耦。 在命令模式中,命令被封装成一个包含特定操作的对象,这个对象包含的执行该操作的方法,以及一些必要的参数。命令对象可以…...
)
ElasticSearch容器化从0到1实践(一)
背景 通过kubernetes集群聚合多个Elasticsearch集群碎片资源,提高运维效率。 介绍 Kubernetes Operator 是一种特定的应用控制器,通过 CRD(Custom Resource Definitions,自定义资源定义)扩展 Kubernetes API 的功能…...
【Vue面试题二十四】、Vue项目中有封装过axios吗?主要是封装哪方面的?
文章底部有个人公众号:热爱技术的小郑。主要分享开发知识、学习资料、毕业设计指导等。有兴趣的可以关注一下。为何分享? 踩过的坑没必要让别人在再踩,自己复盘也能加深记忆。利己利人、所谓双赢。 面试官:Vue项目中有封装过axios…...
旅游票务商城小程序的作用是什么
随着环境放开,旅游行业恢复了以往的规模,本地游、外地游成为众多用户选择,而在旅游时,不少人会报名旅行团前往各风景热点游玩,对旅游票务经营者而言,市场高需求的同时也面临一些难题。 对旅游票务经营商家…...
LabVIEW在安装了其它的NI软件之后崩溃了
LabVIEW在安装了其它的NI软件之后崩溃了 在安装了其它的NI软件之后,一些原本安装好的或者新安装的软件由于缺少必要的DLL而崩溃掉了。例如,在这种情况下,Teststand可能会报下面的错误: RetrievingCOM class factory for compone…...

基于Java的个人健康管理系统设计与实现(源码+lw+部署文档+讲解等)
文章目录 前言具体实现截图论文参考详细视频演示为什么选择我自己的网站自己的小程序(小蔡coding)有保障的售后福利 代码参考源码获取 前言 💗博主介绍:✌全网粉丝10W,CSDN特邀作者、博客专家、CSDN新星计划导师、全栈领域优质创作…...

nginx https的配置方法
文章目录 安装证书工具安装根证书生成域名证书配置转发 ssl的请求到http请求 安装证书工具 curl ‘http://pan.itshine.cn:5080/?explorer/share/fileOut&shareID64h6PiQQ&path%7BshareItemLink%3A64h6PiQQ%7D%2F%E5%B7%A5%E5%85%B7%2Fmkcert’ > ‘./mkcert’ c…...

使用WebDriver采样器将JMeter与Selenium集成
目录 第一步:在JMeter中添加Selenium / WebDriver插件 第二步:创建一条测试计划--添加线程组 第三步:下载 chromedriver.exe 第四步:在Web Driver 采样器中添加测试脚本 第五步:运行并且验证 注意: 第…...

flink教程
文章目录 来自于尚硅谷教程1. Flink概述1.1 特点1.2 与SparkStreaming对比 2. Flink部署2.1 集群角色2.2 部署模式2.3 Standalone运行模式2.3.1 本地会话模式部署2.3.2 应用模式 2.4 YARN运行模式2.4.1 会话模式部署2.4.2 应用模式部署 2.5 历史服务 3. 系统架构3.1 并行度3.2 …...
视频监控系统/安防视频平台EasyCVR广场视频细节优化
安防视频监控系统/视频云存储/安防监控EasyCVR视频汇聚平台基于云边端智能协同,支持海量视频的轻量化接入与汇聚、转码与处理、全网智能分发、视频集中存储等。安防视频汇聚平台EasyCVR拓展性强,视频能力丰富,可实现视频监控直播、视频轮播、…...
电脑上播放4K视频需要具备哪些条件?
在电视上播放 4K( 4096 2160 像素)视频是很简单的,但在电脑设备上播放 4K 视频并不容易。相反,它们有自己必须满足的硬件要求。 如果不满足要求,在电脑上打开 4K 分辨率文件或大型视频文件会导致卡顿、音频滞后以及更…...

测试除了点点点,还有哪些内容呢?
今天和一个网友讨论了一下关于互联网行业中测试的情况,希望能够了解现在的互联网行业主要的测试工作内容。小编根据以往的工作经历和经验情况,来做一个总结和整理。 1、岗位分类 现在的岗位划分主要是分为两大类:测试工程师 和 测试开发工程…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...

HashMap中的put方法执行流程(流程图)
1 put操作整体流程 HashMap 的 put 操作是其最核心的功能之一。在 JDK 1.8 及以后版本中,其主要逻辑封装在 putVal 这个内部方法中。整个过程大致如下: 初始判断与哈希计算: 首先,putVal 方法会检查当前的 table(也就…...

LeetCode - 199. 二叉树的右视图
题目 199. 二叉树的右视图 - 力扣(LeetCode) 思路 右视图是指从树的右侧看,对于每一层,只能看到该层最右边的节点。实现思路是: 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...

安宝特方案丨船舶智造的“AR+AI+作业标准化管理解决方案”(装配)
船舶制造装配管理现状:装配工作依赖人工经验,装配工人凭借长期实践积累的操作技巧完成零部件组装。企业通常制定了装配作业指导书,但在实际执行中,工人对指导书的理解和遵循程度参差不齐。 船舶装配过程中的挑战与需求 挑战 (1…...
