C多线程编程- 近似求解π
本程序使用蒙特卡洛方法估算圆周率(π)。它首先创建了指定数量的线程,每个线程生成一个随机点并检查该点是否在单位圆内。基于这些线程的结果,程序计算在单位圆内的点的比例,并乘以4来估算π的值。为了对比,程序还直接在主线程中(没有并发)进行了相同的π估算过程(由于每次都是生成随机数,所以这个基准也没啥意义hh~)。最后,程序打印出两种方法得到的π值。
#include <pthread.h>
#include <stdio.h>
#include <stdlib.h>struct arg_t {float x;float y;
};void *start(void *arg) {struct arg_t *ll = (struct arg_t *)arg;float x1 = ll->x;float y1 = ll->y;long M = 0;if (x1*x1 + y1*y1 <= 1.0) {M ++;}pthread_exit((void *)M);
}int main(int argc, char **argv) {if (argc < 2) {fprintf(stderr, "Please provide a number as an argument.\n");exit(1);}long N1 = atol(argv[1]);// printf("%ld\n", N1);pthread_t tids[N1];// pai(concurrency)for (long i = 0; i < N1; ++ i) {struct arg_t *arg = malloc(sizeof(struct arg_t));int x = rand();int y = rand();arg->x = 1.0*x / RAND_MAX;arg->y = 1.0*y / RAND_MAX;pthread_create(&tids[i], 0, start, arg);}void *res = 0;long M = 0;for (long i = 0; i < N1; ++ i) {pthread_join(tids[i], &res);M += (long)res;}printf("pai = %f\n", 4.0*M/N1); // concurrency// pai(oracle)M = 0;for (long i = 0; i < N1; ++ i) {int x = rand();int y = rand();float x1 = 1.0*x / RAND_MAX;float y1 = 1.0*y / RAND_MAX;if (x1*x1 + y1*y1 <= 1.0) {M ++;}}printf("pai = %f\n", 4.0*M/N1); // oraclepthread_exit(0);
}
测试一下上述程序:
majn@tiger:~$ ./pai 10000
pai = 3.171200
pai = 3.142000
majn@tiger:~$ ./pai 100000
Segmentation fault (core dumped)
分析Segmentation fault的原因:
在上面的程序中,为每个线程都动态分配了 arg_t 结构的内存,但在线程执行完毕后,这些内存并没有被释放。虽然这不是立即的问题,但长期这样会导致内存泄露。应该在线程函数中或 pthread_join 之后释放这些内存。
改进方案:
一种方法是在线程函数 start 的结尾释放它(插个眼hh~)。但由于在主函数中可能还需要访问这些结构,更安全的方法是在 pthread_join 之后释放这些动态分配的内存。
修改上述代码:
#include <pthread.h>
#include <stdio.h>
#include <stdlib.h>struct arg_t {float x;float y;
};void *start(void *arg) {struct arg_t *ll = (struct arg_t *)arg;float x1 = ll->x;float y1 = ll->y;long M = 0;if (x1*x1 + y1*y1 <= 1.0) {M ++;}pthread_exit((void *)M);
}int main(int argc, char **argv) {if (argc < 2) {fprintf(stderr, "Please provide a number as an argument.\n");exit(1);}long N1 = atol(argv[1]);struct arg_t *args[N1];// printf("%ld\n", N1);pthread_t tids[N1];// pai(concurrency)for (long i = 0; i < N1; ++ i) {args[i] = malloc(sizeof(*args[i]));// struct arg_t *arg = malloc(sizeof(*arg));int x = rand();int y = rand();args[i]->x = 1.0*x / RAND_MAX;args[i]->y = 1.0*y / RAND_MAX;pthread_create(&tids[i], 0, start, args[i]);}void *res = 0;long M = 0;for (long i = 0; i < N1; ++ i) {pthread_join(tids[i], &res);M += (long)res;free(args[i]);}printf("pai = %f\n", 4.0*M/N1); // concurrency// pai(oracle)M = 0;for (long i = 0; i < N1; ++ i) {int x = rand();int y = rand();float x1 = 1.0*x / RAND_MAX;float y1 = 1.0*y / RAND_MAX;if (x1*x1 + y1*y1 <= 1.0) {M ++;}}printf("pai = %f\n", 4.0*M/N1); // oraclepthread_exit(0);
}
这样,每次线程执行完毕并被主线程收回后,对应的动态分配的内存都会被释放。
测试一下修改后的程序:
majn@tiger:~$ ./pai 100000
pai = 3.721760
pai = 3.137640
majn@tiger:~$ ./pai 1000000
Segmentation fault (core dumped)
好好好,这样玩儿是吧。
分析Segmentation fault的原因:
仔细观察上面的程序,我使用了一个固定大小的线程数组:pthread_t tids[N1];。对于大的 N1 值,这可能会导致栈溢出。在大多数系统上,默认的栈大小可能不足以容纳大量的 pthread_t 变量。
改进方案:
考虑动态分配线程ID数组的空间。
#include <pthread.h>
#include <stdio.h>
#include <stdlib.h>struct arg_t {float x;float y;
};void *start(void *arg) {struct arg_t *ll = (struct arg_t *)arg;float x1 = ll->x;float y1 = ll->y;long M = 0;if (x1*x1 + y1*y1 <= 1.0) {M ++;}pthread_exit((void *)M);
}int main(int argc, char **argv) {if (argc < 2) {fprintf(stderr, "Please provide a number as an argument.\n");exit(1);}long N1 = atol(argv[1]);struct arg_t *args[N1];// printf("%ld\n", N1);pthread_t *tids = malloc(N1 * sizeof(pthread_t));// pai(concurrency)for (long i = 0; i < N1; ++ i) {args[i] = malloc(sizeof(*args[i]));// struct arg_t *arg = malloc(sizeof(*arg));int x = rand();int y = rand();args[i]->x = 1.0*x / RAND_MAX;args[i]->y = 1.0*y / RAND_MAX;pthread_create(&tids[i], 0, start, args[i]);}void *res = 0;long M = 0;for (long i = 0; i < N1; ++ i) {pthread_join(tids[i], &res);M += (long)res;free(args[i]);}printf("pai = %f\n", 4.0*M/N1); // concurrency// pai(oracle)M = 0;for (long i = 0; i < N1; ++ i) {int x = rand();int y = rand();float x1 = 1.0*x / RAND_MAX;float y1 = 1.0*y / RAND_MAX;if (x1*x1 + y1*y1 <= 1.0) {M ++;}}printf("pai = %f\n", 4.0*M/N1); // oraclepthread_exit(0);
}
majn@tiger:~$ ./pai 1000000
pai = 3.972176
pai = 3.142136
majn@tiger:~$ ./pai 10000000
Segmentation fault (core dumped)
???不玩儿了!!! 到此为止,我们把输入数据的规模N1从一开始最大接受10000扩大到现在最大接受1000000。
彩蛋: 要不然把为每个线程都动态分配的 arg_t 结构在线程函数 start 的结尾释放试一试?
#include <pthread.h>
#include <stdio.h>
#include <stdlib.h>struct arg_t {float x;float y;
};void *start(void *arg) {struct arg_t *ll = (struct arg_t *)arg;float x1 = ll->x;float y1 = ll->y;long M = 0;if (x1*x1 + y1*y1 <= 1.0) {M ++;}free(arg);pthread_exit((void *)M);
}int main(int argc, char **argv) {if (argc < 2) {fprintf(stderr, "Please provide a number as an argument.\n");exit(1);}long N1 = atol(argv[1]);// printf("%ld\n", N1);// pthread_t tids[N1];pthread_t *tids = malloc(N1 * sizeof(pthread_t));// pi(concurrency)for (long i = 0; i < N1; ++ i) {struct arg_t *arg = malloc(sizeof(struct arg_t));int x = rand();int y = rand();arg->x = 1.0*x / RAND_MAX;arg->y = 1.0*y / RAND_MAX;pthread_create(&tids[i], 0, start, arg);}void *res;long M = 0;for (long i = 0; i < N1; ++ i) {pthread_join(tids[i], &res);M += (long)res;}printf("pai = %f\n", 4.0*M/N1); // concurrency// pi(oracle)M = 0;for (long i = 0; i < N1; ++ i) {int x = rand();int y = rand();float x1 = 1.0*x / RAND_MAX;float y1 = 1.0*y / RAND_MAX;if (x1*x1 + y1*y1 <= 1.0) {M ++;}}printf("pai = %f\n", 4.0*M/N1); // oraclepthread_exit(0);
}
majn@tiger:~$ ./pai_init 10000000
pai = 3.997218
pai = 3.141381
majn@tiger:~$ ./pai_init 100000000
pai = 3.999722
pai = 3.141420
majn@tiger:~$ ./pai_init 1000000000
^C // 时间太长了,不想等了
Amazing!!!怎么这么神奇?
注: 蒙特卡洛方法(Monte Carlo method)是一种通过随机抽样来获得数值解的统计方法。这个方法得名于摩纳哥的蒙特卡洛赌场,因为它大量使用随机性和概率。蒙特卡洛方法在物理学、工程学、经济学和许多其他领域都有广泛的应用。
关键概念和特点:
-
随机抽样:这是蒙特卡洛方法的核心。为了得到一个问题的数值解,这个方法使用随机数或更通常地说,使用伪随机数。
-
统计结果:通过对大量的随机样本进行统计分析,得到的是一个近似解,而不是确切的解。
-
精度与样本数量:通常,随着样本数量的增加,估算的精度也会提高。但是,为了使误差减少到原来的一半,样本数通常需要增加四倍。
-
应用:蒙特卡洛方法在多种应用中都非常有用,尤其是在问题的解析解很难得到或者不存在时。例如,它被用于估算复杂积分、求解难以解析的统计物理问题、进行金融市场模拟等。
-
示例 - 估算π:一个经典的应用是使用蒙特卡洛方法估算π的值。方法是这样的:随机投掷点到单位正方形内,统计落在单位圆内的点的数量。落在圆内的点数与总点数的比例,乘以4,就给出了π的近似值。
简而言之,蒙特卡洛方法是一种利用随机性来求解问题的技术,通过对大量样本的统计分析来获得结果。
相关文章:

C多线程编程- 近似求解π
本程序使用蒙特卡洛方法估算圆周率(π)。它首先创建了指定数量的线程,每个线程生成一个随机点并检查该点是否在单位圆内。基于这些线程的结果,程序计算在单位圆内的点的比例,并乘以4来估算π的值。为了对比,…...

YOLOV7量化第二步: 模型标定
2.模型标定 当然可以,模型量化中的标定(calibration)是一个关键过程,它主要确保在降低计算精度以减少模型大小和提高推理速度的同时,不会显著损害模型的准确性。现在,我将根据您提供的步骤解释这一过程。 …...
前端-uniapp-开发指南
美团外卖微信小程序开发 uniapp-美团外卖微信小程序开发P1 成果展示P2外卖小程序后端,学习给小程序写http接口P3 主界面配置P4 首页组件拆分P13 外卖列表布局筛选组件商家 布局测试数据创建样式 请求商家外卖数据封装请求并发请求 uni-app框架调用https接口 开发小程…...
Java集合类ArrayList的应用-杨辉三角的前n行
目录 一、题目 杨辉三角 二、题解 三、代码 四、总结 一、题目 题目链接:https://leetcode.cn/problems/pascals-triangle/description/ 杨辉三角 题目描述:给定一个非负整数 numRows,生成「杨辉三角」的前 numRows 行。 在「杨…...
C语言-函数
函数是一组一起执行一个任务的语句。每个 C 程序都至少有一个函数,即主函数 main() 。 主函数可以调用其他函数,其他函数也可以相互调用,用户也可以那个自定义函数。 函数声明告诉编译器函数的名称、返回类型和参数。函数定义提供了函数的实…...
蓝桥杯 枚举算法 (c++)
枚举就是根据提出的问题,——列出该问题的所有可能的解,并在逐一列出的过程中,检验每个可能解是否是问题的真正解, 如果是就采纳这个解,如果不是就继续判断下一个。 枚举法一般比较直观,容易理解࿰…...
Wordpress自定义小工具logo调用设置(可视化)
在主题开发中,需要调用网站的logo,最简单的办法就是用wp自带的函数,那就是the_custom_logo(),使用它还可以通过后台-自定义-logo,边修改边预览,还是很香的。 自定义徽标支持应首先使用add_theme_support()添…...
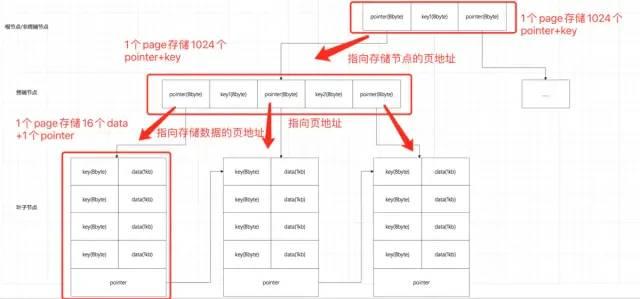
面试常考数据结构:红黑树、B树、B+树各自适用的场景
1. 磁盘基础知识 分页: 现代操作系统都使用虚拟内存来印射到物理内存,内存大小有限且价格昂贵,所以数据的持久化是在磁盘上。虚拟内存、物理内存、磁盘都使用页作为内存读取的最小单位。一般一页为4KB(8个扇区,每个扇…...
Paddle GPU版本需要安装CUDA、CUDNN
完整的教程 深度学习环境配置:linuxwindows系统下的显卡驱动、Anaconda、Pytorch&Paddle、cuda&cudnn的安装与说明 - 知乎这篇文档的内容是尽量将深度学习环境配置(使用GPU)所需要的内容做一些说明,由于笔者只在windows和linux下操作过…...

MYSQL length函数
mysql length函数计算结果的单位是啥,和varchar字段类型的单位是相同的吗? 做了一下实验,结果如下: 1.mysql length 函数计算的是有多少个字符,比如字段值是 permission 则length函数计算结果为10。 2.如果字段类型是…...

uniapp 在android手机上运行tab栏页面跳转问题
【问题描述】: 使用uniapp写的项目,在tab页面,无论使用哪种方式的跳转,只要是在url后面拼接参数,在打包成apk文件后,在手机上面安装使用,都是获取不到susIndex参数的,而在浏览器上面…...

css3 hover效果
CSS3中的:hover伪类用于创建鼠标悬停时的样式效果。当用户将鼠标悬停在页面元素上时,你可以为这些元素定义不同的样式规则,以实现交互效果 /* 一般样式规则 */ element {/* 正常状态下的样式 */ }/* 悬停样式规则 */ element:hover {/* 鼠标悬停时的样式…...
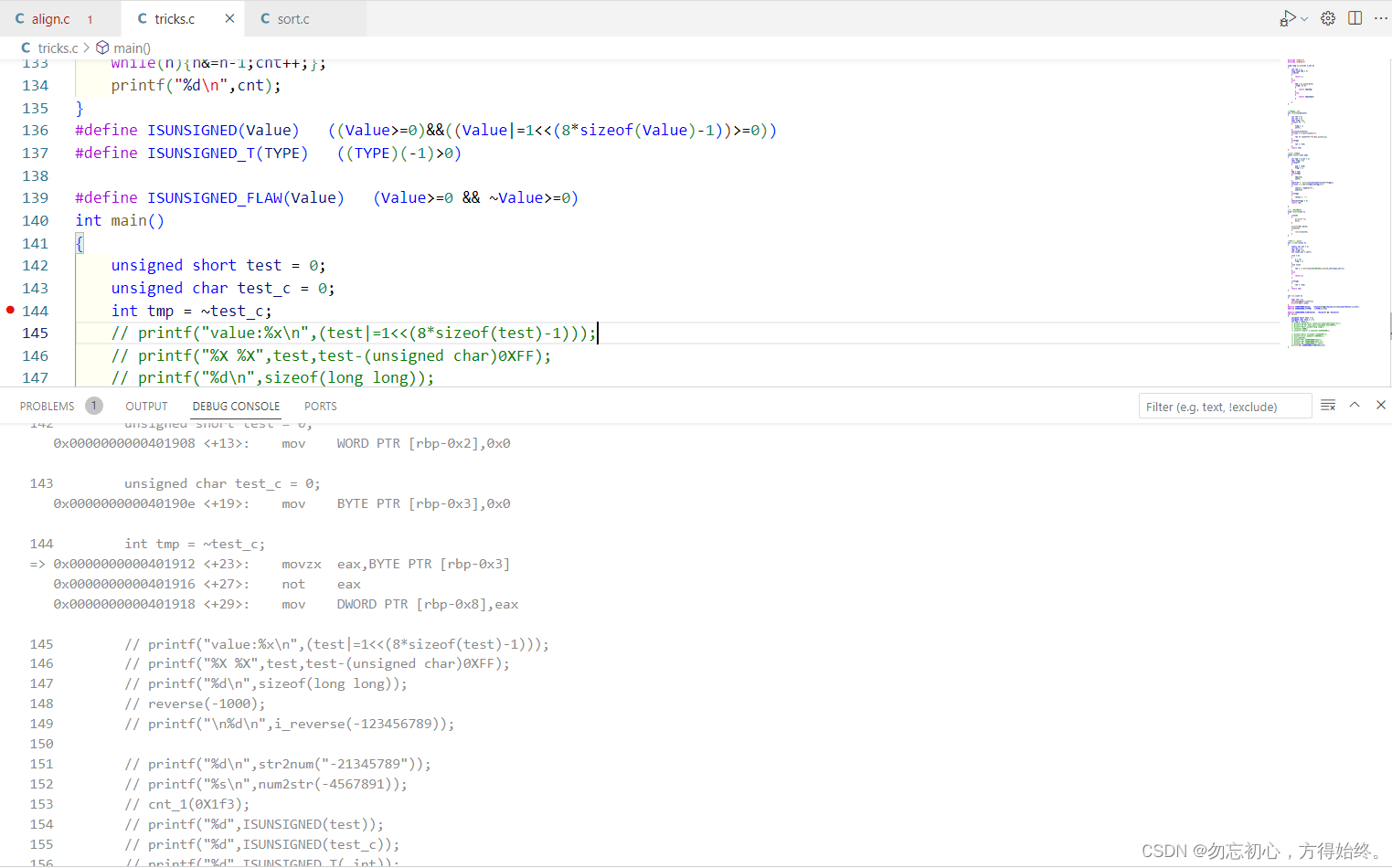
C语言char与short取反以及符号判断问题
这个问题主要是在从对一个变量进行符号判断引出,有一种判断方法是#define ISUNSIGNED(Value) (Value >0 && ~Value >0) 主要是通过将符号位取反然后将变量与0进行比较。传入int与unsigned int结果正确,但是当传入unsigned char 与unsign…...

Gpt-4多模态功能强势上线,景联文科技多模态数据采集标注服务等您来体验!
就在上个月,OpenAI 宣布对ChatGPT 进行重大更新,该模型不仅能够通过文字输入进行识别和分析,还能够通过语音、图像甚至视频等多种模态的输入来获取、识别、分析和输出信息。这一重要技术突破,将促进多模态自然语言处理的发展&…...

【idea】 java: 找不到符号
idea 启动时提示 java: 找不到符号 java: 找不到符号 符号: 方法 getCompanyDisputeCount() 位置: 类型为com.yang.entity.AreaAnalyse的变量 areaAnalyse 在setting ——> Compiler ——>Shared build process VM options: 添加: -Djps.track.ap.dep…...

Flink测试利器之DataGen初探 | 京东云技术团队
什么是 Flinksql Flink SQL 是基于 Apache Calcite 的 SQL 解析器和优化器构建的,支持ANSI SQL 标准,允许使用标准的 SQL 语句来处理流式和批处理数据。通过 Flink SQL,可以以声明式的方式描述数据处理逻辑,而无需编写显式的代码…...
)
linux更换常用软件的默认缓存路径(.conda, .huggingface等)
在使用linux的过程中,我们往往会使用软件安装很多packages,其中的大多数软件(例如conda)会把当前安装的packages缓存起来,以加速之后的相同package的安装。 而很多软件的默认缓存路径是user自己的home路径。下面罗列几…...
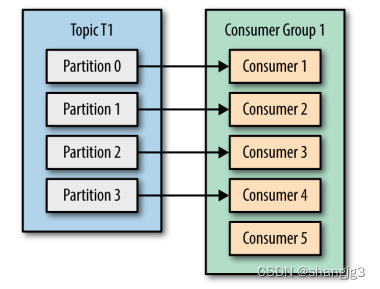
Kafka消费者使用案例
本文代码链接:https://download.csdn.net/download/shangjg03/88422633 1.消费者和消费者群组 在 Kafka 中,消费者通常是消费者群组的一部分,多个消费者群组共同读取同一个主题时,彼此之间互不影响。Kafka 之所以要引入消费者群组…...
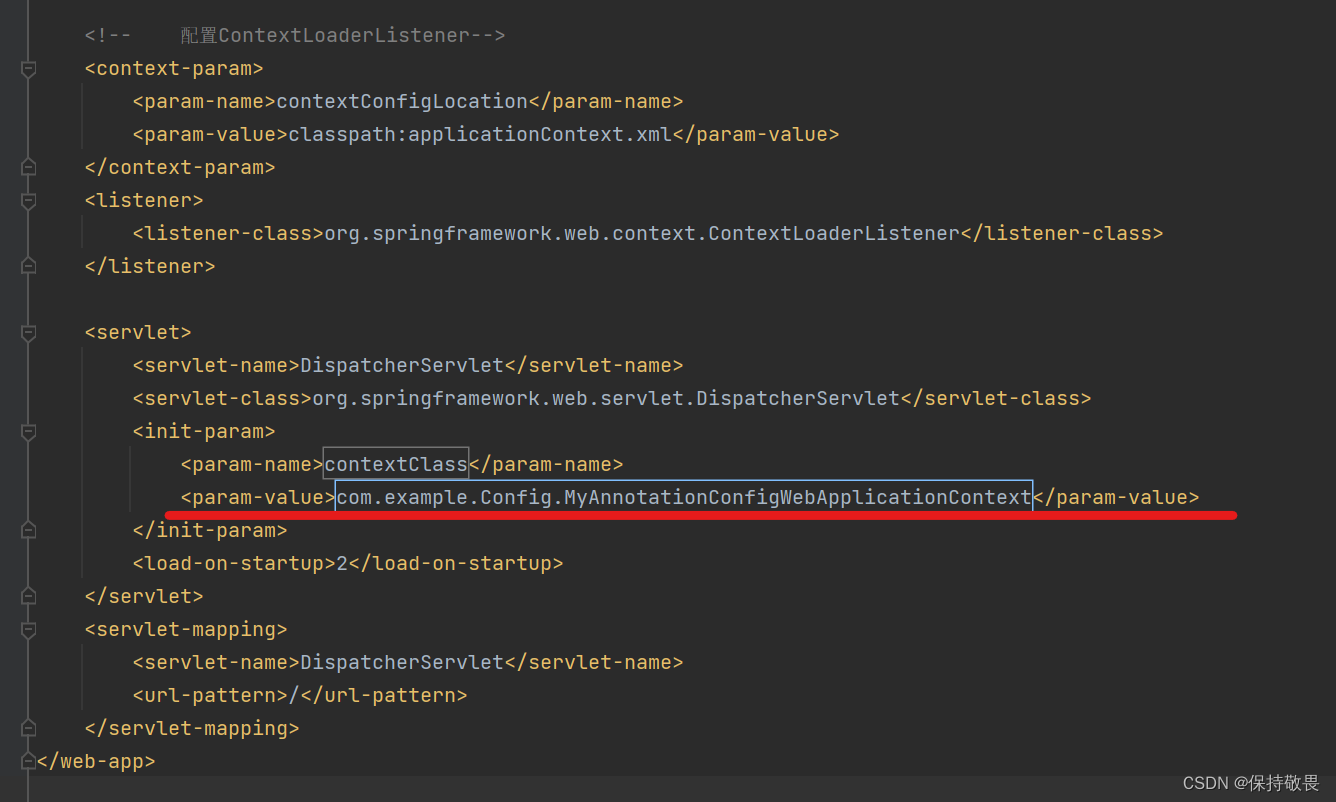
SpringMVC全注解开发
在学习过程中,框架给我们最大的作用,就是想让开发人员尽可能地只将精力放在具体业务功能的实现之上,而对于各种映射关系的配置,统统由框架来进行完成,由此,注解就很好的将映射功能进行实现,并且…...

解决 android Cannot access ‘<init>‘: it is private in
最近要在2个非直接依赖module使用单例,有一种注入依赖的方式可以,但是报了如下错误: Cannot access <init>: it is private in 经过查阅资料,原来是依赖的单例类的构造函数不能使用private,这里做个记录&#…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...

什么?连接服务器也能可视化显示界面?:基于X11 Forwarding + CentOS + MobaXterm实战指南
文章目录 什么是X11?环境准备实战步骤1️⃣ 服务器端配置(CentOS)2️⃣ 客户端配置(MobaXterm)3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果
聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...

CVE-2020-17519源码分析与漏洞复现(Flink 任意文件读取)
漏洞概览 漏洞名称:Apache Flink REST API 任意文件读取漏洞CVE编号:CVE-2020-17519CVSS评分:7.5影响版本:Apache Flink 1.11.0、1.11.1、1.11.2修复版本:≥ 1.11.3 或 ≥ 1.12.0漏洞类型:路径遍历&#x…...

绕过 Xcode?使用 Appuploader和主流工具实现 iOS 上架自动化
iOS 应用的发布流程一直是开发链路中最“苹果味”的环节:强依赖 Xcode、必须使用 macOS、各种证书和描述文件配置……对很多跨平台开发者来说,这一套流程并不友好。 特别是当你的项目主要在 Windows 或 Linux 下开发(例如 Flutter、React Na…...

医疗AI模型可解释性编程研究:基于SHAP、LIME与Anchor
1 医疗树模型与可解释人工智能基础 医疗领域的人工智能应用正迅速从理论研究转向临床实践,在这一过程中,模型可解释性已成为确保AI系统被医疗专业人员接受和信任的关键因素。基于树模型的集成算法(如RandomForest、XGBoost、LightGBM)因其卓越的预测性能和相对良好的解释性…...

【java面试】微服务篇
【java面试】微服务篇 一、总体框架二、Springcloud(一)Springcloud五大组件(二)服务注册和发现1、Eureka2、Nacos (三)负载均衡1、Ribbon负载均衡流程2、Ribbon负载均衡策略3、自定义负载均衡策略4、总结 …...

【1】跨越技术栈鸿沟:字节跳动开源TRAE AI编程IDE的实战体验
2024年初,人工智能编程工具领域发生了一次静默的变革。当字节跳动宣布退出其TRAE项目(一款融合大型语言模型能力的云端AI编程IDE)时,技术社区曾短暂叹息。然而这一退场并非终点——通过开源社区的接力,TRAE在WayToAGI等…...
