KMP 算法 + 详细笔记
给两个字符串,T="AAAAAAAAB",P="AAAAB";

可以暴力匹配,但是太费时和效率不太好。于是KMP问世,我们一起来探究一下吧!!!
(一)最长公共前后缀

- D[i] = p[0]~p[i] 区间(前i+1个字母)所拥有的最大......的长度
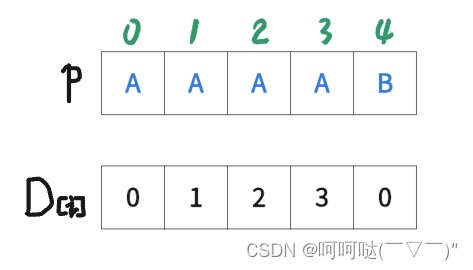
- D[0]=0,表示p[0]~p[0]区间(前1个字母)->也就是 A 所拥有的最长公共前后缀长度为0.
- D[1]=1,表示p[0]~p[1]区间(前2个字母)->也就是 AA 所拥有的最长公共前后缀长度为1.
- D[2]=2,表示p[0]~p[2]区间(前3个字母)->也就是 AAA 所拥有的最长公共前后缀长度为2.
- D[3]=3,表示p[0]~p[3]区间(前4个字母)->也就是 AAAA 所拥有的最长公共前后缀长度为3.
- D[4]=0,表示p[0]~p[4]区间(前5个字母)->也就是 AAAAB 所拥有的最长公共前后缀长度为0.
我们先手算好了P="AAAAB"的D[i]数组(记录最长公共前后缀),继续挖掘,看看有没有好东西!
(1)举个栗子,T = "AAAAAAAAB",P="AAAAB" ,D[i]数组上文已经求出
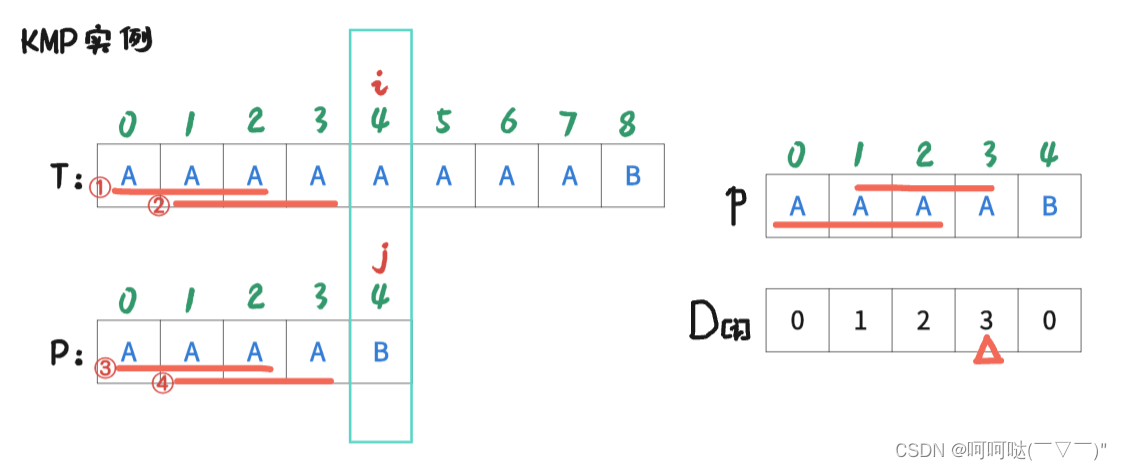
当 i = 4,j = 4 时,T串 和 P串 发生不匹配,此时我们就发现 T[0-3] 和 P[0-3] 是完全匹配的,那就会思考:是否可以用一些方法来跳过已经判断是能匹配的范围呢?
在 j = 4时,j-1=3,D[3] = 3,也就是意味着P[0]~P[3] 区间(前4个字母)所拥有的最大公共前后缀长度为3.
于是从图中我们可以看到标注为① ② ③ ④ 条红色的线,表示 T 和 P的前后缀相同
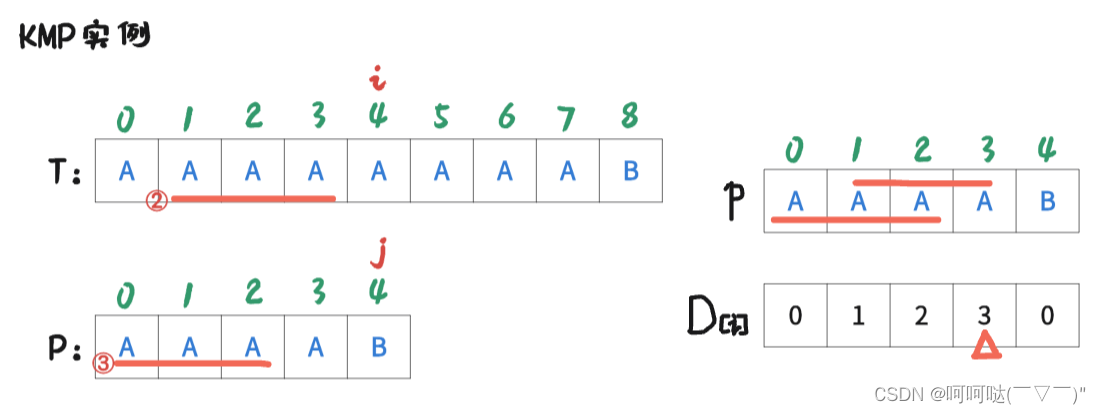 着重看②和③这两条,我们可以让 j = 3,即进行操作是:j = D[4-1]; 再让T[i] 和 P[j] 去判断是否匹配。
着重看②和③这两条,我们可以让 j = 3,即进行操作是:j = D[4-1]; 再让T[i] 和 P[j] 去判断是否匹配。
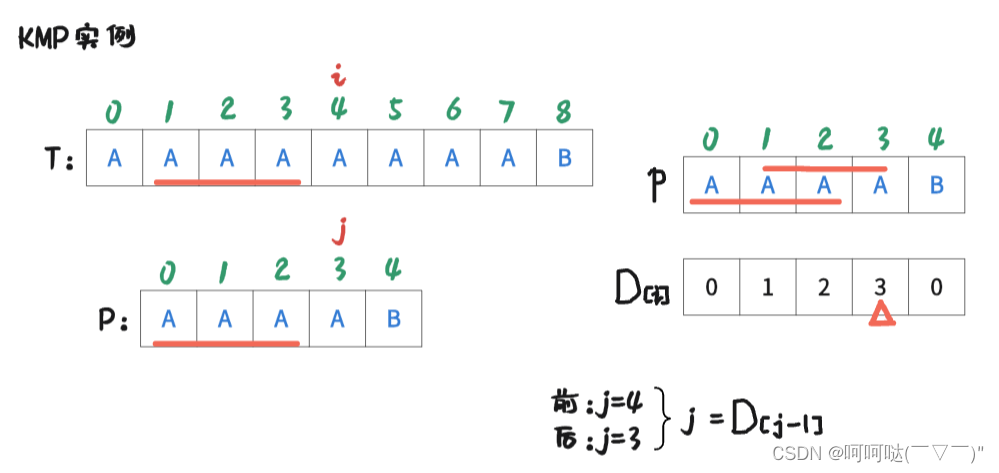
此时 i = 4 , j = 3时,T[4] = P[3],是匹配的,那么让 i++, j++,可得到下图:
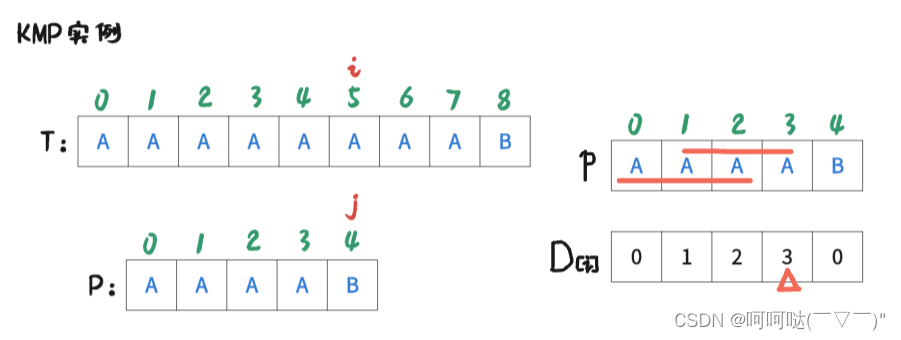
此时 i = 5 , j = 4时,T[5] ≠ P[4],是不匹配的,此时跟前面的操作一样。进行操作是:j = D[4-1]; 再让T[i] 和 P[j] 去判断是否匹配。可得到下图:
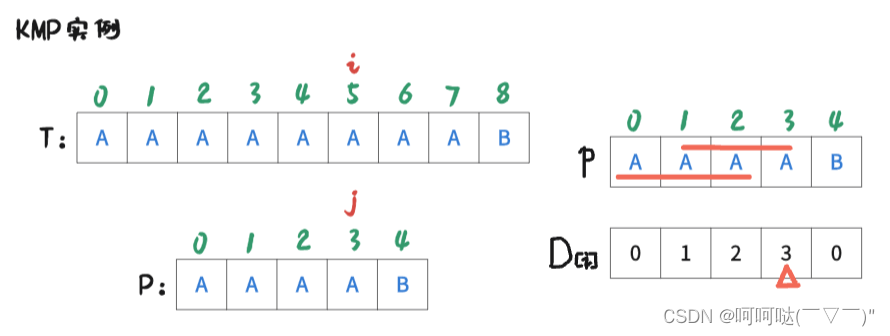
此时 i = 5 , j = 3时,T[5] = P[3],是匹配的,那么让 i++, j++,可得到下图:
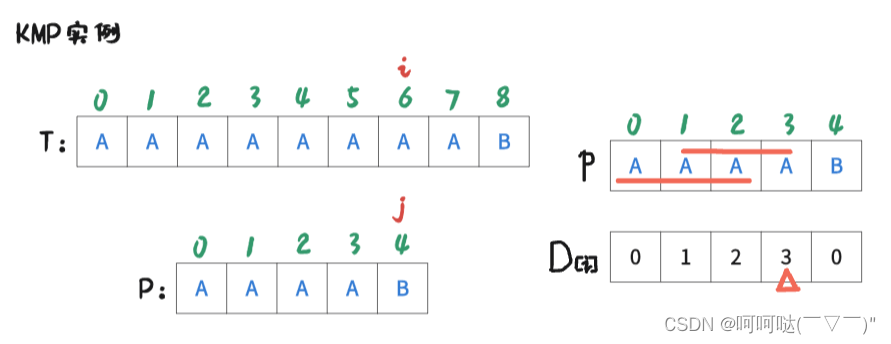
此时 i = 6 , j = 4时,T[6] ≠ P[4],是不匹配的,此时跟前面的操作一样。进行操作是:j = D[4-1]; 再让T[i] 和 P[j] 去判断是否匹配。可得到下图:
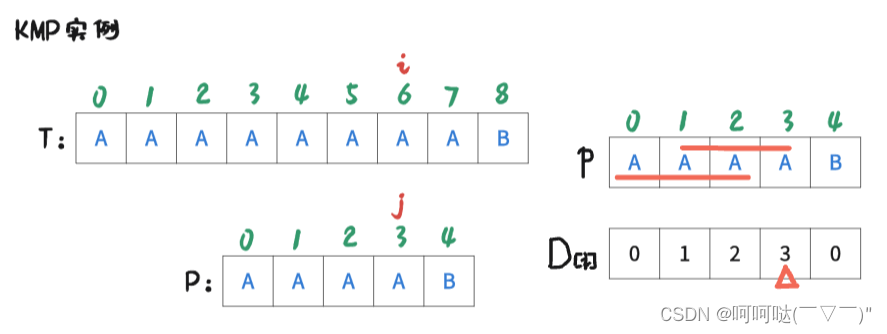
此时 i = 6 , j = 3时,T[6] = P[3],是匹配的,那么让 i++, j++,可得到下图:
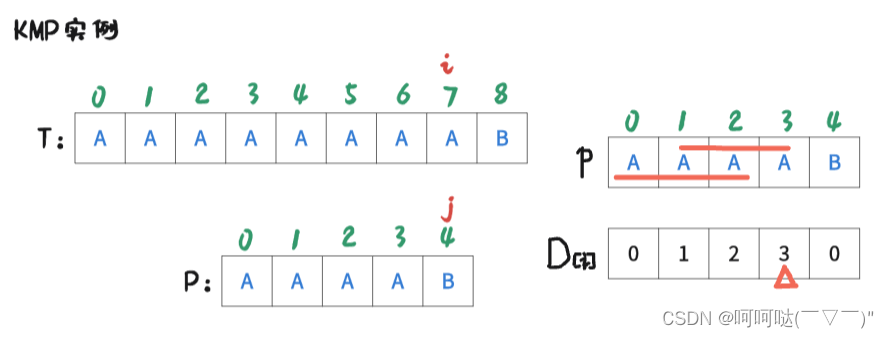
此时 i = 7 , j = 4时,T[7] ≠ P[4],是不匹配的,此时跟前面的操作一样。进行操作是:j = D[4-1]; 再让T[i] 和 P[j] 去判断是否匹配。可得到下图:
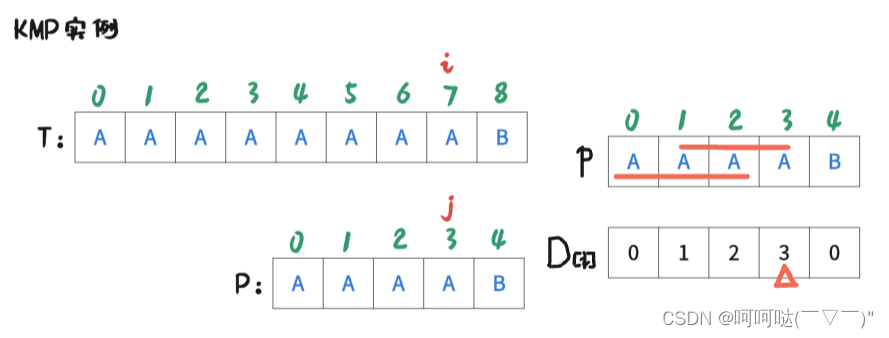
此时 i = 7 , j = 3时,T[7] = P[3],是匹配的,那么让 i++, j++,可得到下图:
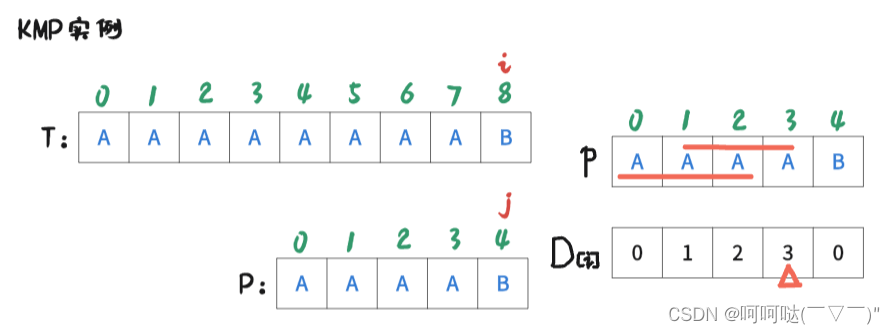
此时 i = 8 , j = 4时,T[8] = P[4],是匹配的,那么让 i++, j++,可得到下图:
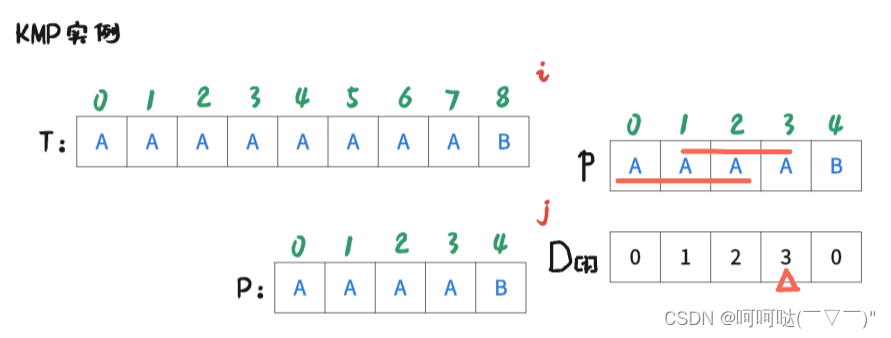
此时 i = 9(越界), j = 5(越界),终止!
总结:发现已经匹配成功的部分,它所拥有的最大公共前后缀就不用重复进行比较了,不用再花费无效的时间进行比较了,最大公共前后缀越长,那它所省略的就越多,效率也就越高。相对于暴力匹配来说,效率提升也就越高。
kmp核心思路的关键所在:
- 1.必须理解 D[j] 的意义:P串的前 j+1个字母,即 P[0]~P[j] 所拥有的最大公共前后缀
- 2.匹配到T[i] != P[j]失败时,想一想P[j]是不是P串的第j+1个字母,是不是也意味着:P[0]~P[j-1]的这前j个字母已经匹配成功了
- 3.P[0]~P[j-1]的这前 j 个字母的最大公共前后缀 = D[j-1]
----来自B站Up邋遢大王233的评论区回复
(二)KMP Code
- D[i] = P[0]至P[i],P串前 i+1 个字母拥有的最大公共前后缀的长度
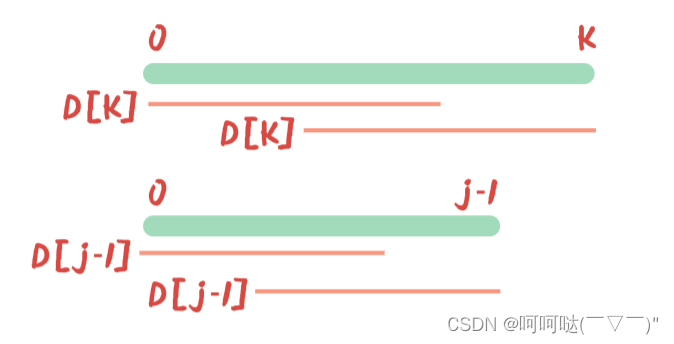
D[k] 表示 P[0]~P[k]时,前 k+1 个 字母拥有的最大公共前后缀的长度
同理,D[j-1]: P[0]~P[j-1], 前 j 个 字母拥有的最大公共前后缀的长度
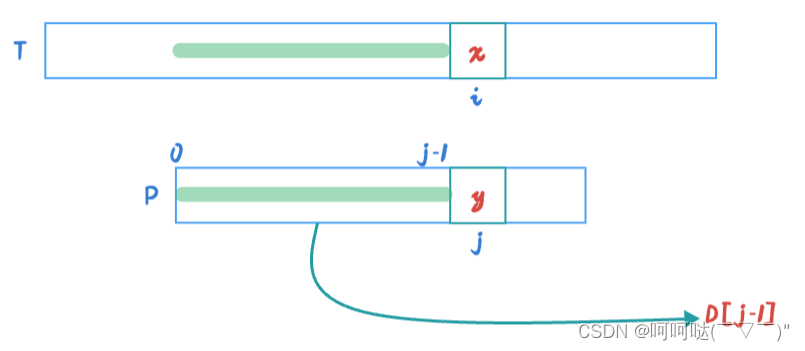
结合上图,D[j-1]:P[0]~P[j-1],前 j 个 字母拥有的最大公共前后缀的长度
在上图我们知道,在 i 位置的 x 和 j 位置的 y 匹配失败。此时该怎么办呢?为了更好的观察规律,我们不妨设D[j-1] = 3,也就是说P[0]~P[j-1],前 j 个 字母拥有的最大公共前后缀的长度为3。此时如下图:
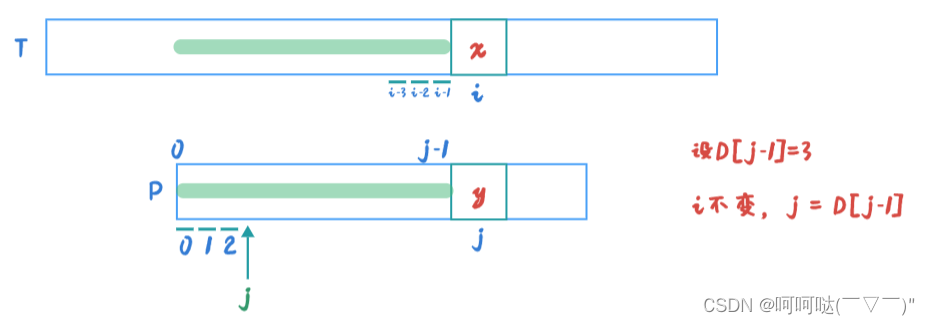
那么让 j = D[j-1] = 3,此时 j 的位置 更新到下标为3这个位置,再从j = 3这个位置与 T 串的 x进行匹配判断
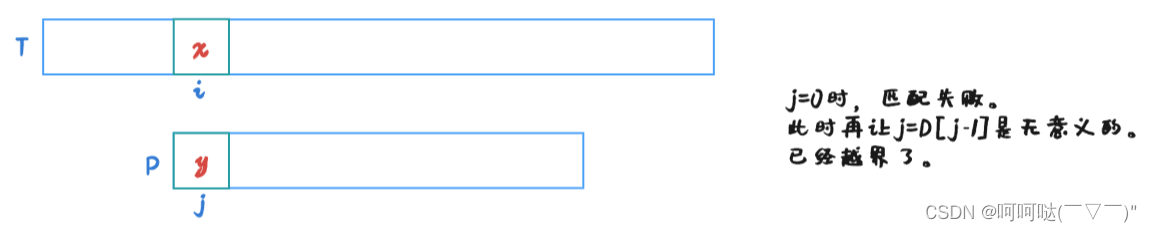
若 j = 0时,匹配失败。此时再让 j = D[j-1]是无意义的。已经越界了。那怎么办呢?

若 j = 0时,匹配失败。让 j 不变,i++
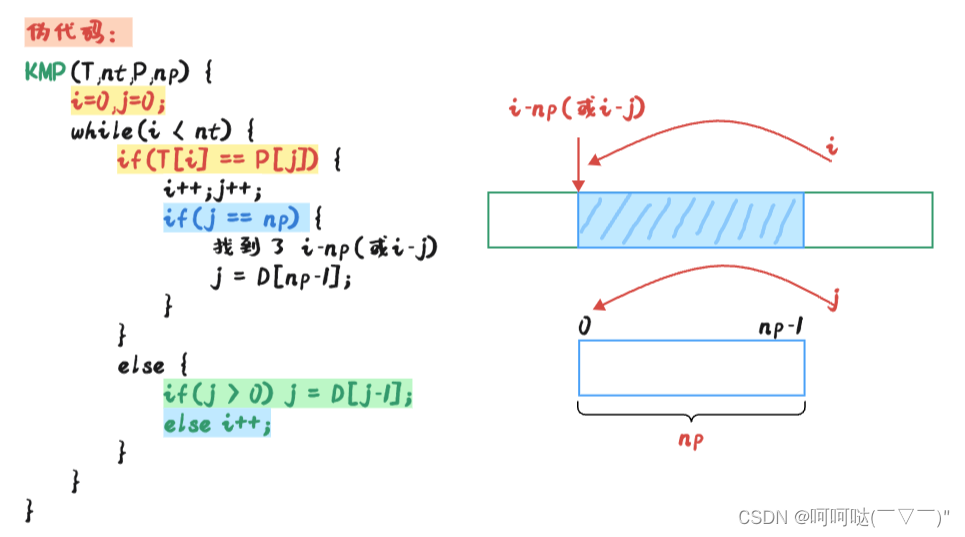 j == np (视频中没有介绍后续如何继续匹配,所以一旦匹配成功一次就结束算法了)。而匹配失败时j只可能减少不可能增加第一次匹配成功后,后续想要继续的话,继续 j = D[j-1] 就可以了(此时必然 j = np ,所以写成 j=D[np-1] 也对) ----来自B站Up邋遢大王233的评论区回复
j == np (视频中没有介绍后续如何继续匹配,所以一旦匹配成功一次就结束算法了)。而匹配失败时j只可能减少不可能增加第一次匹配成功后,后续想要继续的话,继续 j = D[j-1] 就可以了(此时必然 j = np ,所以写成 j=D[np-1] 也对) ----来自B站Up邋遢大王233的评论区回复
未完待续,明天继续编辑~
参考和推荐视频:kmp_5_最大公共前后缀代码实现_哔哩哔哩_bilibili![]() https://www.bilibili.com/video/BV1iJ411a7Kb?p=5&vd_source=a934d7fc6f47698a29dac90a922ba5a3
https://www.bilibili.com/video/BV1iJ411a7Kb?p=5&vd_source=a934d7fc6f47698a29dac90a922ba5a3
相关文章:
KMP 算法 + 详细笔记
给两个字符串,T"AAAAAAAAB",P"AAAAB"; 可以暴力匹配,但是太费时和效率不太好。于是KMP问世,我们一起来探究一下吧!!! (一)最长公共前后缀 D[i] p[…...
基于主动移频法与AFD孤岛检测的单相并网逆变器matlab仿真
微❤关注“电气仔推送”获得资料(专享优惠) 仿真模型 算法介绍 (1)仿真模型由单相电网、逆变器、滤波环节、PI控制器、PWM生成器、锁相环、AFD控制器s函数、测量模块等构成; (2)采用主动移频法(AFD)进行孤岛检测; (3)相应速度…...
MIT 6.S081 Operating System/Fall 2020 macOS搭建risc-v与xv6开发调试环境
文章目录 本机配置安装环境Homebrew执行安装脚本查看安装是否成功 RISC-V tools执行brew的安装脚本 QEMUXV6 测试有用的参考链接(感谢前辈)写在结尾 本机配置 电脑型号:Apple M2 Pro 2023 操作系统:macOS Ventura 13.4 所以我的电…...

JMeter定时器
一. 同步定时器(Synchronizing Timer) (在Loadrunner中叫做集合点) 思考: 如何模拟多个用户同时抢一个红包?如何测试电商网站中抢购活动、秒杀活动? 1.1 介绍 Sync Timer的目的是阻塞线程,直…...

zookeeper应用场景(二)
单机环境下可以利用jvm级别的锁,比如synchronized、Lock等来实现锁,如果是多机部署就需要一个共享数据存储区域来实现分布式锁 一、分布式锁实现方式 1、基于数据库实现分布式锁 可以用数据库唯一索引来实现 2、基于redis实现分布式锁 redis实现的分…...

Android webView加载高德地图定位不显示问题
如果只显示地图 val webView: WebView findViewById(R.id.webView)webView.settings.javaScriptEnabled truewebView.loadUrl("https://test.cn")//h5地址 如果需要定位,则需要加以下代码,否则不弹窗 webView.webChromeClient object : We…...
94. 二叉树的中序遍历(递归+迭代)
题目链接:力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台 解题思路: 方法一:递归 中序遍历的操作定义为,若二叉树为空,则空操作,否则: 中序遍历左子树访问根节点中…...
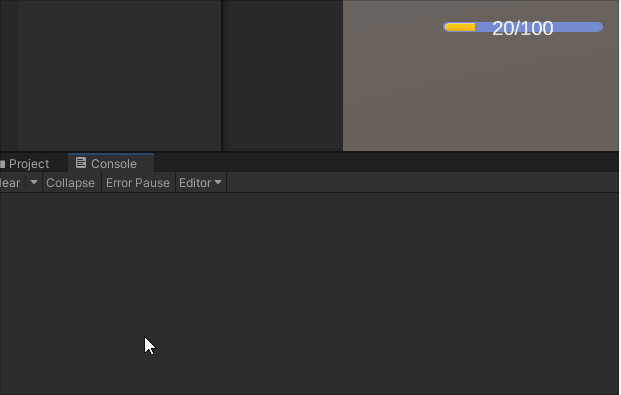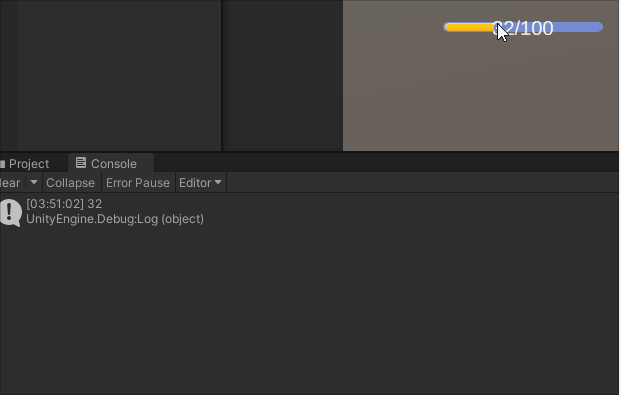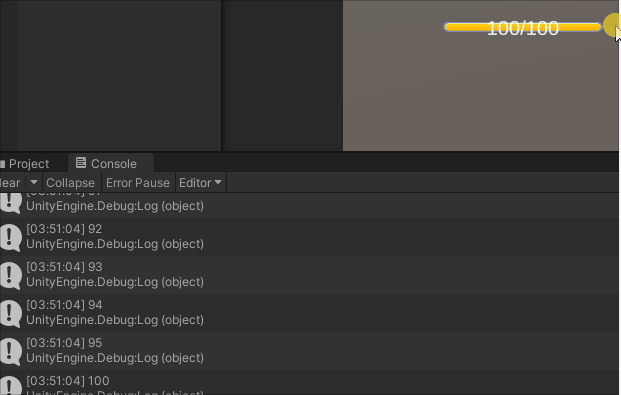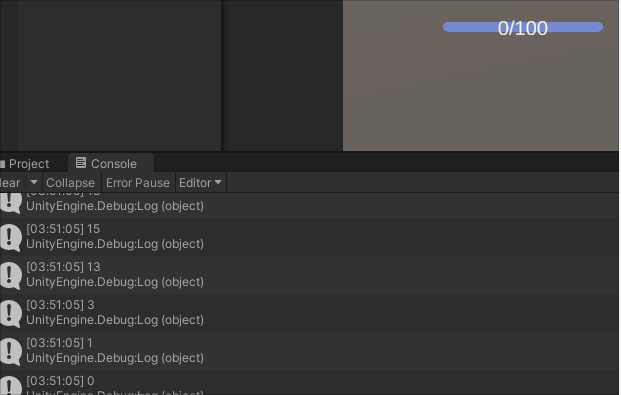
UGUI交互组件Slider
一.Slider对象的结构 对象介绍Slider附加Slider组件Background背景Fill Area填充范围Fill填充对象Handle Slider Area滑块移动范围Handle滑块 二.Slider组件属性 属性说明Fill Rect关联填充对象Handle Rect关联滑块对象Direction设置方向Min Value最大取值Max Value最小取值Wh…...

JAVA经典百题之按位或运算符 `|的使用
当学习Java语言中的按位或运算符 | 时,需要理解其用途、应用场景、示例源代码以及相应的注意事项。以下是一篇关于Java语言按位或运算符的详细文章,包括示例源代码和注释。 Java语言中的按位或运算符 | 按位或运算符 | 是Java语言中用于对二进制位进行…...

C多线程编程- 近似求解π
本程序使用蒙特卡洛方法估算圆周率(π)。它首先创建了指定数量的线程,每个线程生成一个随机点并检查该点是否在单位圆内。基于这些线程的结果,程序计算在单位圆内的点的比例,并乘以4来估算π的值。为了对比,…...

YOLOV7量化第二步: 模型标定
2.模型标定 当然可以,模型量化中的标定(calibration)是一个关键过程,它主要确保在降低计算精度以减少模型大小和提高推理速度的同时,不会显著损害模型的准确性。现在,我将根据您提供的步骤解释这一过程。 …...
前端-uniapp-开发指南
美团外卖微信小程序开发 uniapp-美团外卖微信小程序开发P1 成果展示P2外卖小程序后端,学习给小程序写http接口P3 主界面配置P4 首页组件拆分P13 外卖列表布局筛选组件商家 布局测试数据创建样式 请求商家外卖数据封装请求并发请求 uni-app框架调用https接口 开发小程…...
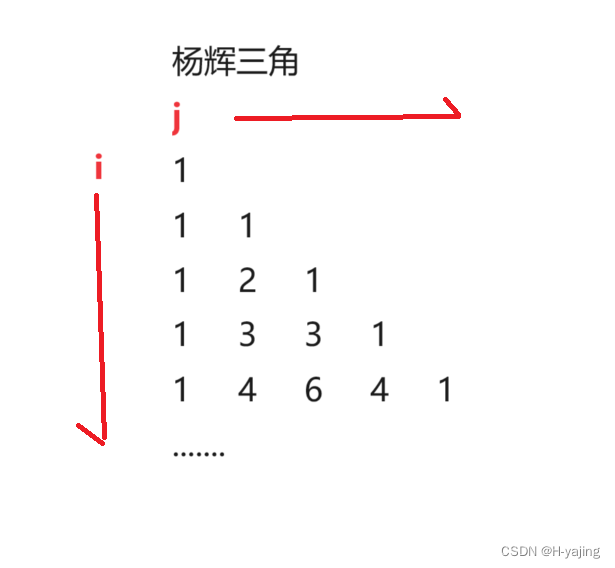
Java集合类ArrayList的应用-杨辉三角的前n行
目录 一、题目 杨辉三角 二、题解 三、代码 四、总结 一、题目 题目链接:https://leetcode.cn/problems/pascals-triangle/description/ 杨辉三角 题目描述:给定一个非负整数 numRows,生成「杨辉三角」的前 numRows 行。 在「杨…...
C语言-函数
函数是一组一起执行一个任务的语句。每个 C 程序都至少有一个函数,即主函数 main() 。 主函数可以调用其他函数,其他函数也可以相互调用,用户也可以那个自定义函数。 函数声明告诉编译器函数的名称、返回类型和参数。函数定义提供了函数的实…...
蓝桥杯 枚举算法 (c++)
枚举就是根据提出的问题,——列出该问题的所有可能的解,并在逐一列出的过程中,检验每个可能解是否是问题的真正解, 如果是就采纳这个解,如果不是就继续判断下一个。 枚举法一般比较直观,容易理解࿰…...
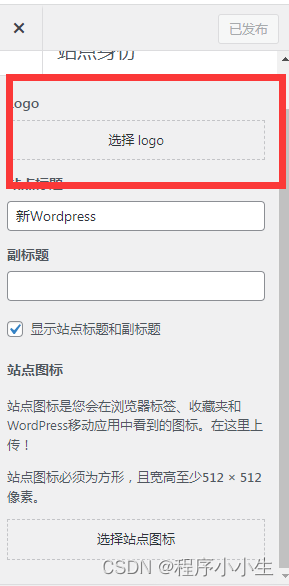
Wordpress自定义小工具logo调用设置(可视化)
在主题开发中,需要调用网站的logo,最简单的办法就是用wp自带的函数,那就是the_custom_logo(),使用它还可以通过后台-自定义-logo,边修改边预览,还是很香的。 自定义徽标支持应首先使用add_theme_support()添…...
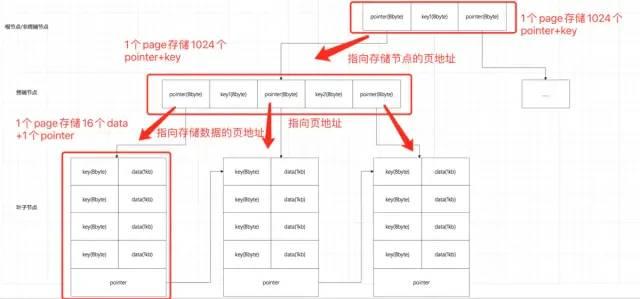
面试常考数据结构:红黑树、B树、B+树各自适用的场景
1. 磁盘基础知识 分页: 现代操作系统都使用虚拟内存来印射到物理内存,内存大小有限且价格昂贵,所以数据的持久化是在磁盘上。虚拟内存、物理内存、磁盘都使用页作为内存读取的最小单位。一般一页为4KB(8个扇区,每个扇…...
Paddle GPU版本需要安装CUDA、CUDNN
完整的教程 深度学习环境配置:linuxwindows系统下的显卡驱动、Anaconda、Pytorch&Paddle、cuda&cudnn的安装与说明 - 知乎这篇文档的内容是尽量将深度学习环境配置(使用GPU)所需要的内容做一些说明,由于笔者只在windows和linux下操作过…...

MYSQL length函数
mysql length函数计算结果的单位是啥,和varchar字段类型的单位是相同的吗? 做了一下实验,结果如下: 1.mysql length 函数计算的是有多少个字符,比如字段值是 permission 则length函数计算结果为10。 2.如果字段类型是…...

uniapp 在android手机上运行tab栏页面跳转问题
【问题描述】: 使用uniapp写的项目,在tab页面,无论使用哪种方式的跳转,只要是在url后面拼接参数,在打包成apk文件后,在手机上面安装使用,都是获取不到susIndex参数的,而在浏览器上面…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...

Python+ZeroMQ实战:智能车辆状态监控与模拟模式自动切换
目录 关键点 技术实现1 技术实现2 摘要: 本文将介绍如何利用Python和ZeroMQ消息队列构建一个智能车辆状态监控系统。系统能够根据时间策略自动切换驾驶模式(自动驾驶、人工驾驶、远程驾驶、主动安全),并通过实时消息推送更新车…...

从 GreenPlum 到镜舟数据库:杭银消费金融湖仓一体转型实践
作者:吴岐诗,杭银消费金融大数据应用开发工程师 本文整理自杭银消费金融大数据应用开发工程师在StarRocks Summit Asia 2024的分享 引言:融合数据湖与数仓的创新之路 在数字金融时代,数据已成为金融机构的核心竞争力。杭银消费金…...

Linux系统部署KES
1、安装准备 1.版本说明V008R006C009B0014 V008:是version产品的大版本。 R006:是release产品特性版本。 C009:是通用版 B0014:是build开发过程中的构建版本2.硬件要求 #安全版和企业版 内存:1GB 以上 硬盘…...

libfmt: 现代C++的格式化工具库介绍与酷炫功能
libfmt: 现代C的格式化工具库介绍与酷炫功能 libfmt 是一个开源的C格式化库,提供了高效、安全的文本格式化功能,是C20中引入的std::format的基础实现。它比传统的printf和iostream更安全、更灵活、性能更好。 基本介绍 主要特点 类型安全:…...

C++实现分布式网络通信框架RPC(2)——rpc发布端
有了上篇文章的项目的基本知识的了解,现在我们就开始构建项目。 目录 一、构建工程目录 二、本地服务发布成RPC服务 2.1理解RPC发布 2.2实现 三、Mprpc框架的基础类设计 3.1框架的初始化类 MprpcApplication 代码实现 3.2读取配置文件类 MprpcConfig 代码实现…...
