数学建模——平稳时间序列分析方法
目录
1、平稳性的Daniel检验
(1)Spearman相关系数假设检验
(2)时间序列平稳性的Danniel假设检验
案例
【模型分析】
1、原始数据at的平稳性检验
2、一阶差分序列的平稳性检验
3、二阶差分序列的平稳性检验
4、建立AR(2)模型
【模型求解】
1、平稳性的Daniel检验
(1)Spearman相关系数假设检验
设二维总体(X,Y)的样本观测值为:(x1,y1),(x2,y2),…,(xn,yn), 得各分量X,Y的样本为(x1,…,xn),(y1,…,yn),设(x1,…,xn)的秩统计量为R1,R2,…,Rn;(y1,y2,…,yn)的秩统计量为S1,S2,…,Sn。当X,Y紧密相关时,这两组秩统计量也是紧密相关的
向量的秩:
向量的秩是指矩阵中非零行向量组成的最大线性无关组的向量个数。在线性代数中,我们常常将向量表示为列向量,也即 n×1的矩阵。
一个矩阵的秩是指它的列向量或行向量中线性无关的向量的个数。可以用初等变换将矩阵变换为行最简形,行最简形的矩阵就是阶梯型矩阵。阶梯型矩阵的非零行的个数即为矩阵的秩。
对于 n × m 的矩阵 A,它的秩记作 rank(A)。秩的性质包括:
1. rank(A) ≤ min(n, m),即矩阵的秩不会超过它的行数和列数中的较小值。
2. 对于同型矩阵 A 和 B,如果 A 可以通过基本行(列)运算转换为 B,那么它们的秩相等。
3. 对于同型矩阵 A 和 B,有 rank(A + B) ≤ rank(A) + rank(B)。秩的求解方法包括高斯消元法、矩阵的特征值特征向量等。
(x1,…,xn)的秩统计量为R1,R2,…,Rn:
在统计学中,对于给定的一组数据 (x1, x2, ..., xn),可以计算出一系列的秩统计量 R1, R2, ..., Rn,用于描述数据的排序性质。每个秩统计量 Ri 表示对应数据 xi 在原始数据中的排名。
秩统计量常用于非参数统计方法,特别是在样本数据不服从正态分布或具有明显偏斜的情况下。它们提供了一种基于排序的方法来分析数据,不受异常值的影响,并可以在不依赖具体分布的情况下得到一些推断性的结论。
以下是对每个秩统计量的解释:
- R1 表示 x1 在排序后的数据中的排名。
- R2 表示 x2 在排序后的数据中的排名。
- ...
- Rn 表示 xn 在排序后的数据中的排名。对于具体的数据样本,可以通过对原始数据进行排序,然后分配相应的秩统计量来计算每个数据的排名。排名方式可以根据需要选择是按升序还是降序进行排列。
通过计算秩统计量,可以进行一系列非参数的统计检验、回归分析和描述性统计分析,例如秩和检验、秩相关分析和秩和相关系数等。这些方法可以提供一种有效的手段来处理各种类型的数据,特别是对于小样本或不满足正态分布假设的情况下。
定义Spearman相关系数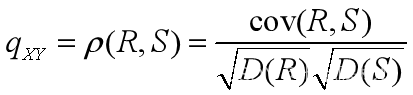
经过运算,可以证明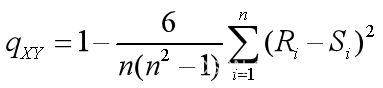
对Spearman相关系数,可以作假设检验: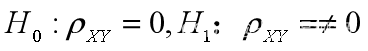
在H0成立时,统计量
对给你的显著水平α,查自由度为n-2的t分布的临界值tα/2(n-2),当|T|≤tα/2(n-2)时,接受H0,否则决绝H0.
(2)时间序列平稳性的Danniel假设检验
设时间序列样本a1,a2,…,an为Xt的样本,记at的秩为Rt=R(at),考虑变量(t,Rt),t=1,2,…,n的Spearman相关系数为
构造统计量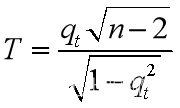
作假设检验:H0:序列Xt平稳;H1:序列Xt非平稳(上升或下降)
(H0的意思t和Rt不相关,即相关系数为0,H1的意思t和Rt相关,即Rt随t增大呈线性递增或递减)
Danniel检验方法:对给定的显著系数α,查自由度为n-2的t分布的临界值tα/2(n-2),若统计量T满足|T|>tα/2(n-2),则拒绝H 0,即认为序列非平稳,若|T|≤tα/2(n-2),接受H0,即Xt是平稳的。
案例
| 月份t | 1 | 2 | 3 | 4 | 5 | 6 |
| 销售收入yt | 533.8 | 574.6 | 606.9 | 649.8 | 705.1 | 772.0 |
| 月份t | 7 | 8 | 9 | 10 | 11 | |
| 销售收入yt | 816.4 | 892.7 | 963.9 | 1015.1 | 1102.7 |
用AR模型预测12月份的销售额。
【模型分析】
1、原始数据at的平稳性检验
设1-11月份销售数据为at,根据公式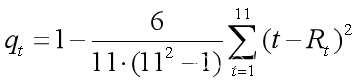 计算得到Spearman相关系数为qt=1.根据公式
计算得到Spearman相关系数为qt=1.根据公式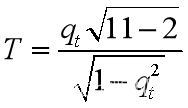
α=0.05,计算得到T统计量为+∞,即|T|> tα/2(11-2)=2.2622,即拒绝H0,认为Xt非平稳。即at非平稳时间序列。
at=[533.8 574.6 606.9 649.8 705.1 772 816.4 892.7 963.9 1015.1 1102.7];
Rt=tiedrank(at);
n=length(Rt);
t=1:n;
dt=t-Rt;
qt=1-6/n/(n^2-1)*sum(dt.^2);
T=qt*(n-2)^0.5/(1-qt^2)^0.5;
2、一阶差分序列的平稳性检验
令bt=at-at-1,t=2,3,…,11,将bt代入【4】和【5】,计算得到T统计量为T= 3.6934>tα/2(10-2)=2.3,即bt也非平稳序列。
at=[533.8 574.6 606.9 649.8 705.1 772 816.4 892.7 963.9 1015.1 1102.7];
bt=diff(at);
Rt=tiedrank(bt);
n=length(Rt);
t=1:n;
dt=t-Rt;
qt=1-6/n/(n^2-1)*sum(dt.^2);
T=qt*(n-2)^0.5/(1-qt^2)^0.5;
3、二阶差分序列的平稳性检验
取ct=bt-bt-1,t=2,3,…,10,将ct代入【4】和【5】,计算,得到统计量T= 0.4934<tα/2(9-2)=2.36,即ct是平稳序列。
at=[533.8 574.6 606.9 649.8 705.1 772 816.4 892.7 963.9 1015.1 1102.7];
bt=diff(at);
ct=diff(bt);
Rt=tiedrank(ct);
n=length(Rt);
t=1:n;
dt=t-Rt;
qt=1-6/n/(n^2-1)*sum(dt.^2);
T=qt*(n-2)^0.5/(1-qt^2)^0.5;
4、建立AR(2)模型
根据上面的检验,可建立自回归模型AR(2)对at进行预测: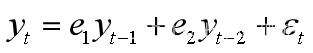 e1,e2是待定参数,εt是随机扰动。
e1,e2是待定参数,εt是随机扰动。
【模型求解】
根据表中数据,采用最小二乘拟合,求得模型为
at=[533.8 574.6 606.9 649.8 705.1 772 816.4 892.7 963.9 1015.1 1102.7];
m=ar(at',2);
>> mm =
Discrete-time AR model: A(z)y(t) = e(t)A(z) = 1 - 1.95 z^-1 + 0.9431 z^-2
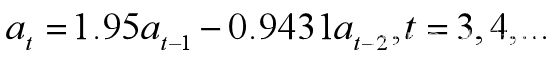
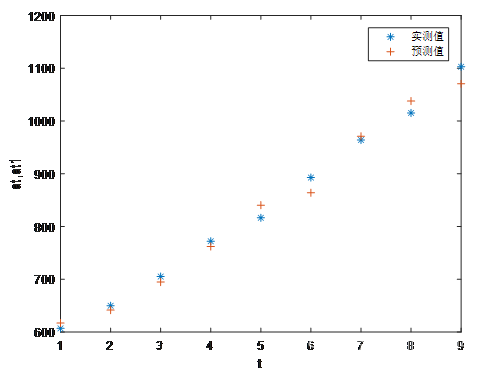
将a10,a11代入上公式,预测12月份销售额为a12=1192.9。并将预测值和实测值对比显示在下图。
at=[533.8 574.6 606.9 649.8 705.1 772 816.4 892.7 963.9 1015.1 1102.7];
for k=3:12at1(k)=1.95*at(k-1)-0.9431*at(k-2);
end
t=1:9;
at=at(3:end);
at1=at1(3:end-1);
plot(t,at,‘*’,t,at1,‘+’),legend(‘实测值’,‘预测值')
另外:matlab时间序列工具箱有AR(2)拟合函数m=ar(at',2);
相关文章:

数学建模——平稳时间序列分析方法
目录 1、平稳性的Daniel检验 (1)Spearman相关系数假设检验 (2)时间序列平稳性的Danniel假设检验 案例 【模型分析】 1、原始数据at的平稳性检验 2、一阶差分序列的平稳性检验 3、二阶差分序列的平稳性检验 4、建立AR&#…...

Vuex使用方式及异步问题处理
🎬 艳艳耶✌️:个人主页 🔥 个人专栏 :《Spring与Mybatis集成整合》《Vue.js使用》 ⛺️ 生活的理想,为了不断更新自己 ! 目录 1.Vuex简介: 2.vuex获取值 2.1安装 2.2.菜单栏 2.3.模块 2.4使用 3.改…...
【Vue面试题二十七】、你了解axios的原理吗?有看过它的源码吗?
文章底部有个人公众号:热爱技术的小郑。主要分享开发知识、学习资料、毕业设计指导等。有兴趣的可以关注一下。为何分享? 踩过的坑没必要让别人在再踩,自己复盘也能加深记忆。利己利人、所谓双赢。 面试官:说下你的vue项目的目录结…...

LocalDateTime与时间戳
众所周知,如果想把 LocalDateTime 转为时间戳,需要先指定时区,然后才能转为时间戳,例如: LocalDateTime localDateTime LocalDateTime.now(); ZonedDateTime zonedDateTime localDateTime.atZone(ZoneId.systemDe…...
【Power BI】Power BI 入门指南:版本、下载和报表创建的步骤
文章目录 一、前言二、了解 Power BI 版本三、下载 Power BI Desktop四、如何开始使用 Power BI Desktop五、在 Power BI Desktop 中创建报表六、文末总结 一、前言 Power BI 是微软于 2013 年推出的产品,为一款商业智能与数据可视化工具。它通过引人注目的视觉效果…...

代码随想录算法训练营第23期day21| 235. 二叉搜索树的最近公共祖先 、701.二叉搜索树中的插入操作、450.删除二叉搜索树中的节点
目录 一、(leetcode 235)二叉搜索树的最近公共祖先 二、(leetcode 701)二叉搜索树中的插入操作 三、(leetcode 450)删除二叉搜索树中的节点 一、(leetcode 235)二叉搜索树的最近公…...

小程序页面路由传参的方法?
小程序页面路由传参的方法有三种: 1.URL参数传递:通过在页面跳转的URL中携带参数实现传参。可以使用wx.navigateTo或wx.redirectTo等跳转方法,并在URL中添加参数。 示例: // PageA.wxml <button bindtap"navigateToPage…...
Ubuntu下安装Python
Ubuntu下安装Python 预备知识一、Python安装Python 二、Anaconda安装Anaconda卸载Anaconda 三、Miniconda安装Miniconda 四、异同比较 预备知识 (1) Python是一种编程语言。 (2) Anaconda是一款包管理工具,用来管理Python及其他语言的安装包,预装了很多…...
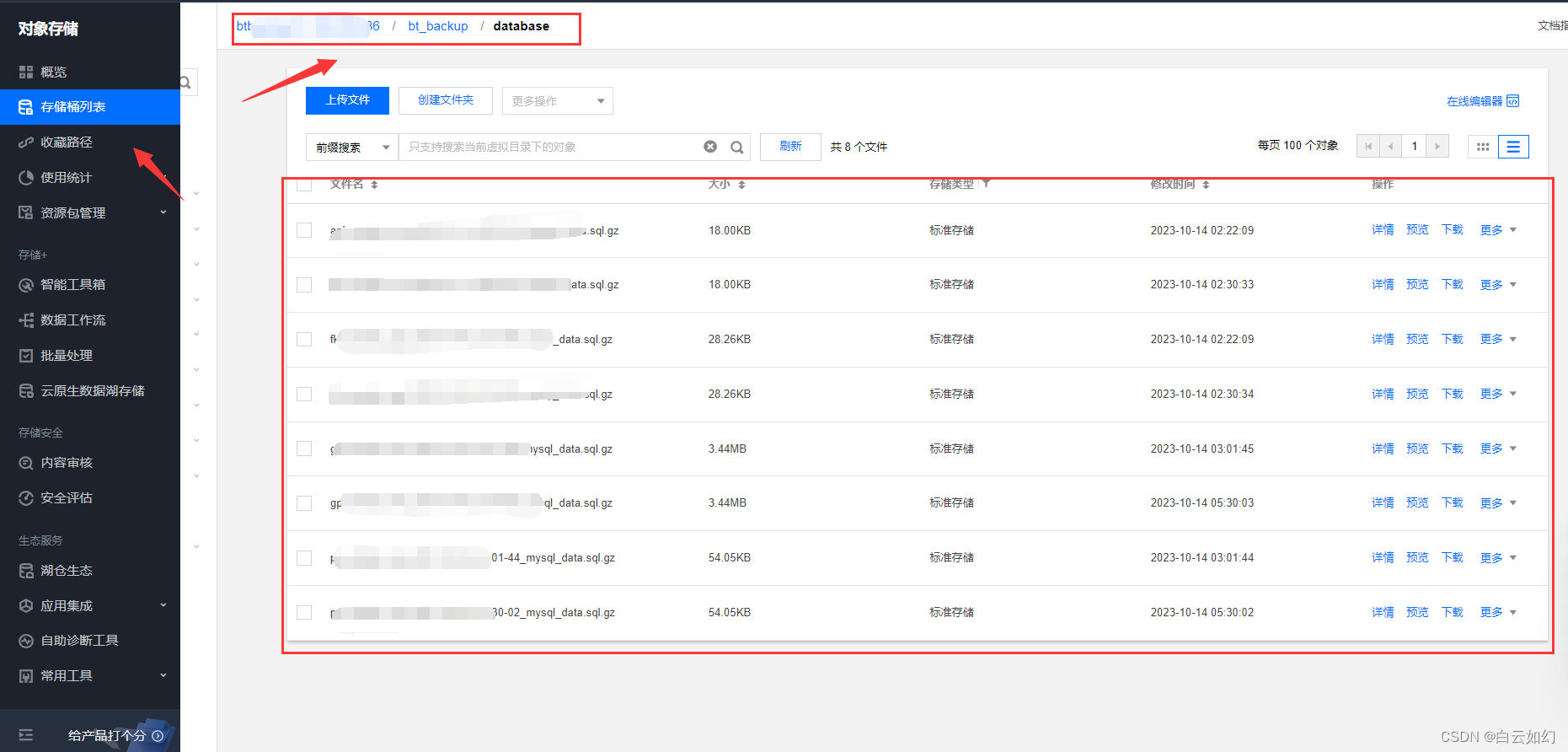
宝塔使用腾讯COS存储实现自动备份服务器网站数据图文教程
一、进入宝塔安装腾讯COS 点击设置打开后需要配置以下cos参数 二、腾讯云创建COS存储桶 选择私有读写,其他默认就行 三、创建访问密钥 四、配置宝塔中腾讯COS相关设置 很多人是配置错误导致无法正常链接cos region为cos存储桶所属地域 Bucker为存储桶名称 五、…...

npm命令介绍
npm 描述:Node Package Manager (NPM) 是 Node.js 的包管理器,用于安装、管理和发布 JavaScript 包。示例:npm -v npm access 描述:控制包的访问权限。需要管理员或拥有特定权限的用户才能执行。示例:npm access pu…...

openGauss学习笔记-100 openGauss 数据库管理-管理数据库安全-客户端接入之用SSL进行安全的TCP/IP连接
文章目录 openGauss学习笔记-100 openGauss 数据库管理-管理数据库安全-客户端接入之用SSL进行安全的TCP/IP连接100.1 背景信息100.2 前提条件100.3 注意事项100.4 操作步骤100.5 相关参考 openGauss学习笔记-100 openGauss 数据库管理-管理数据库安全-客户端接入之用SSL进行安…...
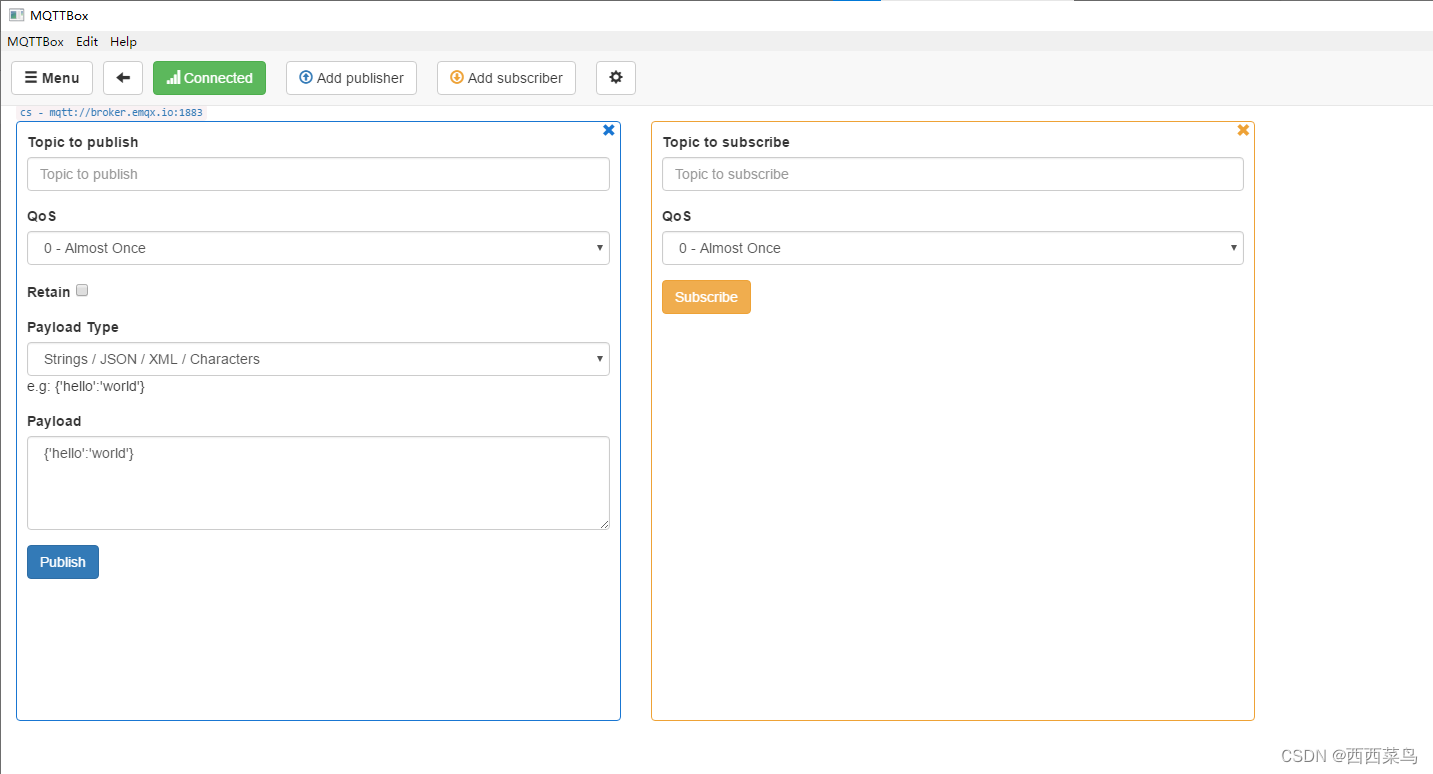
ESP8266 Node Mcu开发板连接WIFI并上报数据到MQTT服务器——物联网应用开发
一、前言 本文主要介绍关于ESP8266 Node Mcu开发板如何连接WIFI并将本地采集的数据上传到MQTT服务器中。 大家调试可以使用MQTTBox 二、WIFI连接 首先,导入WIFI连接所需的头文件,引入所需库。 #include <ESP8266WiFi.h> 声明字符串常量࿰…...

苍穹外卖(八) 使用WebSocket协议完成来单提醒及客户催单功能
WebSocket介绍 WebSocket 是基于 TCP 的一种新的网络协议。它实现了浏览器与服务器全双工通信(双向传输)——浏览器和服务器只需要完成一次握手,两者之间就可以创建持久性的连接, 并进行双向数据传输。 HTTP协议和WebSocket协议对比: HTTP…...

网站如何应对网络流量攻击
网络安全问题中,受到流量攻击是一种常见挑战。以下是一系列的专业建议,帮助您预防和减轻这类攻击,从而确保您的网站和数据的安全。 使用 Web 应用程序防火墙 (WAF) Web 应用程序防火墙是一项专门的安全工具,能够检测和拦截恶意流…...

设置Json序列化时字段的顺序
1. 背景 在部分使用场景(如元数据驱动,后台接口仅返回序列化后的json字符串,前端需要根据每个字段在前端呈现),需要手动设置字段的长度。通常情况下,框架是有默认的顺序,如 jackson 默认使用字…...

AcWing5277. 三元组
给定一个长度为 n 的正整数数组 a1,a2,…,an 请你计算,一共有多少个三元组 (i,j,k)(1≤i<j<k≤n),使得 ai⋅aj⋅ak 为最小可能值。 输入格式 第一行包含整数 n。 第二行包含 n 个正整数 a1,a2,…,an。 输出格式 一个整…...
【LeetCode热题100】--121.买卖股票的最佳时机
121.买卖股票的最佳时机 class Solution {public int maxProfit(int[] prices) {int minprice Integer.MAX_VALUE;int maxprofit 0;for(int i 0;i<prices.length;i){if(prices[i] < minprice){minprice prices[i]; //找到最小值}else if(prices[i] - minprice > ma…...

高精度计算
1.高精度加法: 两个非常大的数相加. 代码如下: #include <iostream> #include <cstring> #include <algorithm> #include <vector>using namespace std;vector<int> add(vector<int>&A,vector<int>&am…...
KMP 算法 + 详细笔记
给两个字符串,T"AAAAAAAAB",P"AAAAB"; 可以暴力匹配,但是太费时和效率不太好。于是KMP问世,我们一起来探究一下吧!!! (一)最长公共前后缀 D[i] p[…...
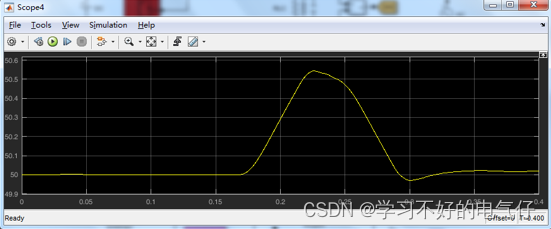
基于主动移频法与AFD孤岛检测的单相并网逆变器matlab仿真
微❤关注“电气仔推送”获得资料(专享优惠) 仿真模型 算法介绍 (1)仿真模型由单相电网、逆变器、滤波环节、PI控制器、PWM生成器、锁相环、AFD控制器s函数、测量模块等构成; (2)采用主动移频法(AFD)进行孤岛检测; (3)相应速度…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...
)
postgresql|数据库|只读用户的创建和删除(备忘)
CREATE USER read_only WITH PASSWORD 密码 -- 连接到xxx数据库 \c xxx -- 授予对xxx数据库的只读权限 GRANT CONNECT ON DATABASE xxx TO read_only; GRANT USAGE ON SCHEMA public TO read_only; GRANT SELECT ON ALL TABLES IN SCHEMA public TO read_only; GRANT EXECUTE O…...

高危文件识别的常用算法:原理、应用与企业场景
高危文件识别的常用算法:原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件,如包含恶意代码、敏感数据或欺诈内容的文档,在企业协同办公环境中(如Teams、Google Workspace)尤为重要。结合大模型技术&…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...

Java面试专项一-准备篇
一、企业简历筛选规则 一般企业的简历筛选流程:首先由HR先筛选一部分简历后,在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如:Boss直聘(招聘方平台) 直接按照条件进行筛选 例如:…...
-HIve数据分析)
大数据学习(132)-HIve数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言Ǵ…...

分布式增量爬虫实现方案
之前我们在讨论的是分布式爬虫如何实现增量爬取。增量爬虫的目标是只爬取新产生或发生变化的页面,避免重复抓取,以节省资源和时间。 在分布式环境下,增量爬虫的实现需要考虑多个爬虫节点之间的协调和去重。 另一种思路:将增量判…...

【无标题】湖北理元理律师事务所:债务优化中的生活保障与法律平衡之道
文/法律实务观察组 在债务重组领域,专业机构的核心价值不仅在于减轻债务数字,更在于帮助债务人在履行义务的同时维持基本生活尊严。湖北理元理律师事务所的服务实践表明,合法债务优化需同步实现三重平衡: 法律刚性(债…...
