C语言:冒泡排序
C语言 基础开发----目录
冒泡排序
1. 原理
对一个有n个数据的数组进行遍历,依次对相邻两个数据进行比较大小,若大的数据在前面则交换位置(升序),完成一次遍历后数组中最大的数据到了数组的末尾位置,就象水底下的气泡一样逐渐 向上冒泡。
然后再对前面n-1个数据进行相同的遍历,一共完成n-1次遍历就实现了排序完成。
2. 举例说明
将5个无序的数列 {6 , 8 , -12 , 0 , -2},使用冒泡排序法(升序)将其排列成一个从小到大的有序数列。
第一次遍历,做 4 次比较,将第一大的数据放到倒数第一的位置
原始数据: 6 8 0 -2 -12
第一次遍历: 6 0 -2 -12 8
第二次遍历,做 3 次比较,将第二大的数据放到倒数第二的位置
原始数据:6 8 0 -2 -12
第一次遍历: 6 0 -2 -12 8
第二次遍历: 0 -2 -12 6 8
第三次遍历,做 2 次比较,将第三大的数据放到倒数第三的位置
原始数据:6 8 0 -2 -12
第一次遍历: 6 0 -2 -12 8
第二次遍历:0 -2 -12 6 8
第三次遍历: -2 -12 0 6 8
第四次遍历,做 1 次比较,将第四大的数据放到倒数第四的位置
原始数据:6 8 0 -2 -12
第一次遍历: 6 0 -2 -12 8
第二次遍历:0 -2 -12 6 8
第三次遍历: -2 -12 0 6 8
第四次遍历: -12 -2 0 6 8
3. 程序代码
具体代码如下:
//升序排序:大的在后面
void BubbleSort_Rise(int *data, int Length)
{int j,i;int t;//临时变量 for(i=0;i<Length-1;i++){for(j=0;j<Length-1-i;j++){ //如果前面的数大于的后面的数,就交换if(data[j]>data[j+1]){t = data[j];data[j] = data[j+1];data[j+1] = t;}}}
}int main(int argc, char *argv[])
{int n;int Tdata[5] = {6,8,0,-2,-12};int DataLen = sizeof(Tdata) / sizeof(int); // 5 数组大小BubbleSort_Rise(Tdata,DataLen);//数组默认是地址传递 (指针)printf("升序排序结果:");for(n=0;n<DataLen;n++){printf(" %d",Tdata[n]); }printf("\n"); return 0;
}
运行结果如下:

相关文章:

C语言:冒泡排序
C语言 基础开发----目录 冒泡排序 1. 原理 对一个有n个数据的数组进行遍历,依次对相邻两个数据进行比较大小,若大的数据在前面则交换位置(升序),完成一次遍历后数组中最大的数据到了数组的末尾位置,就象水…...
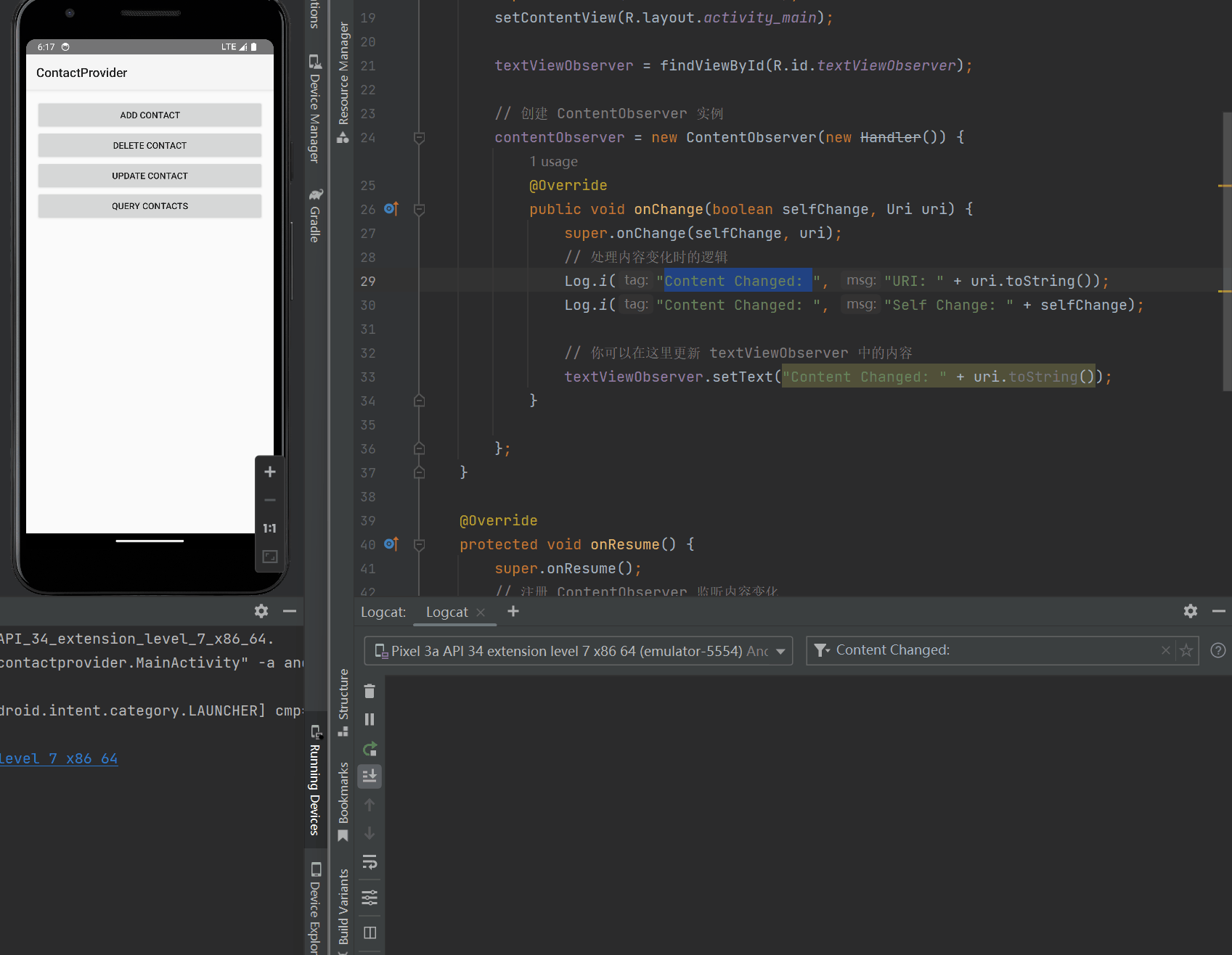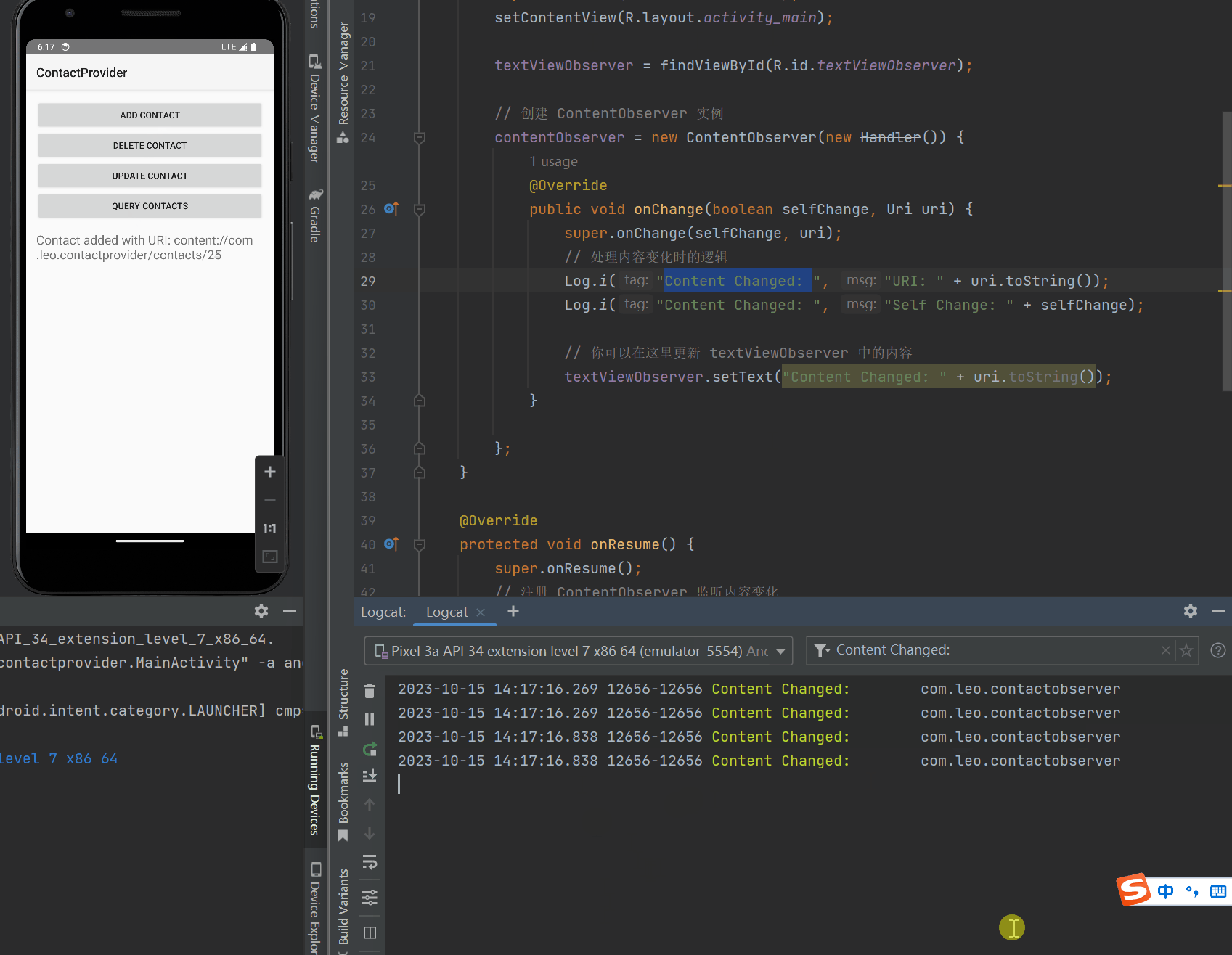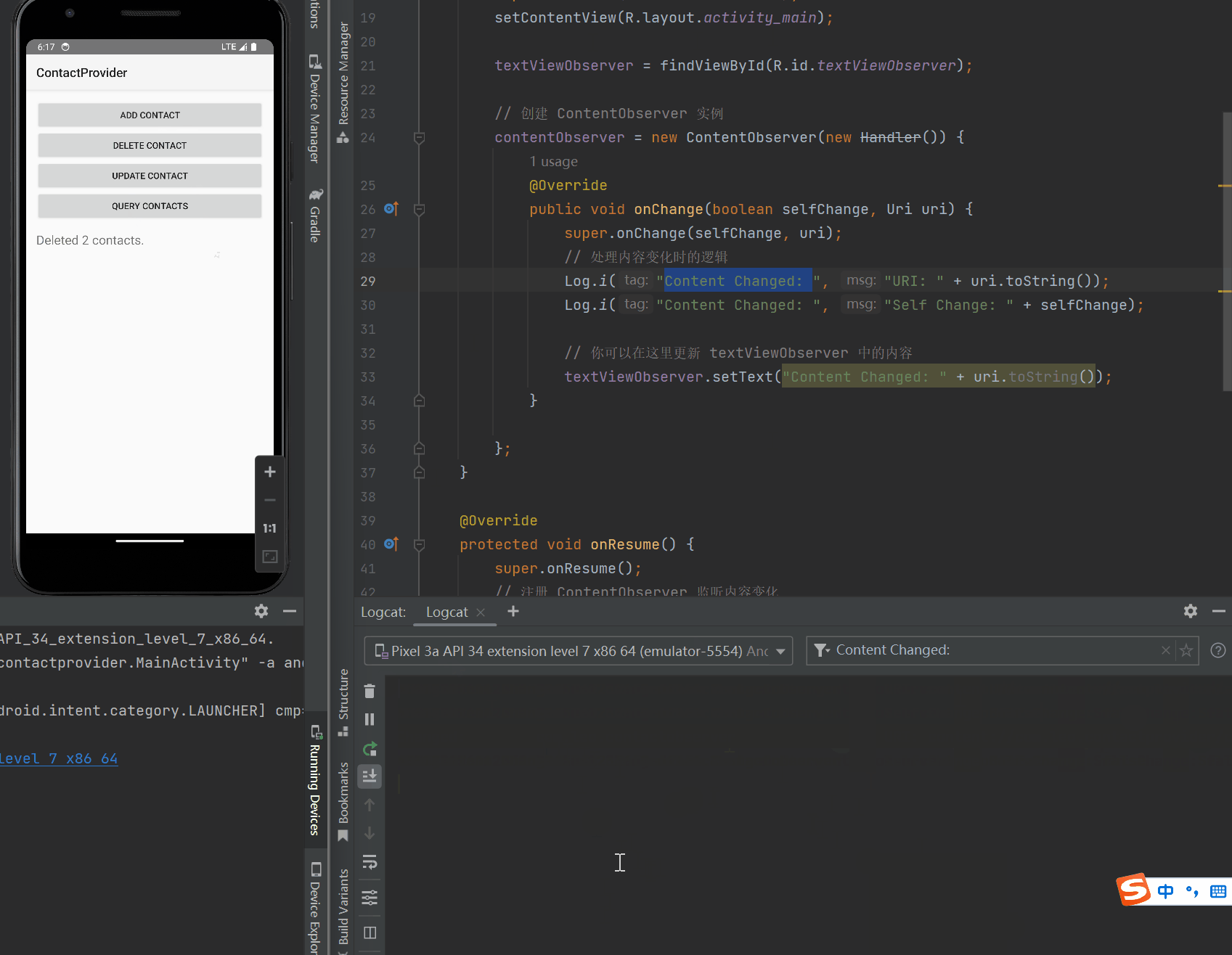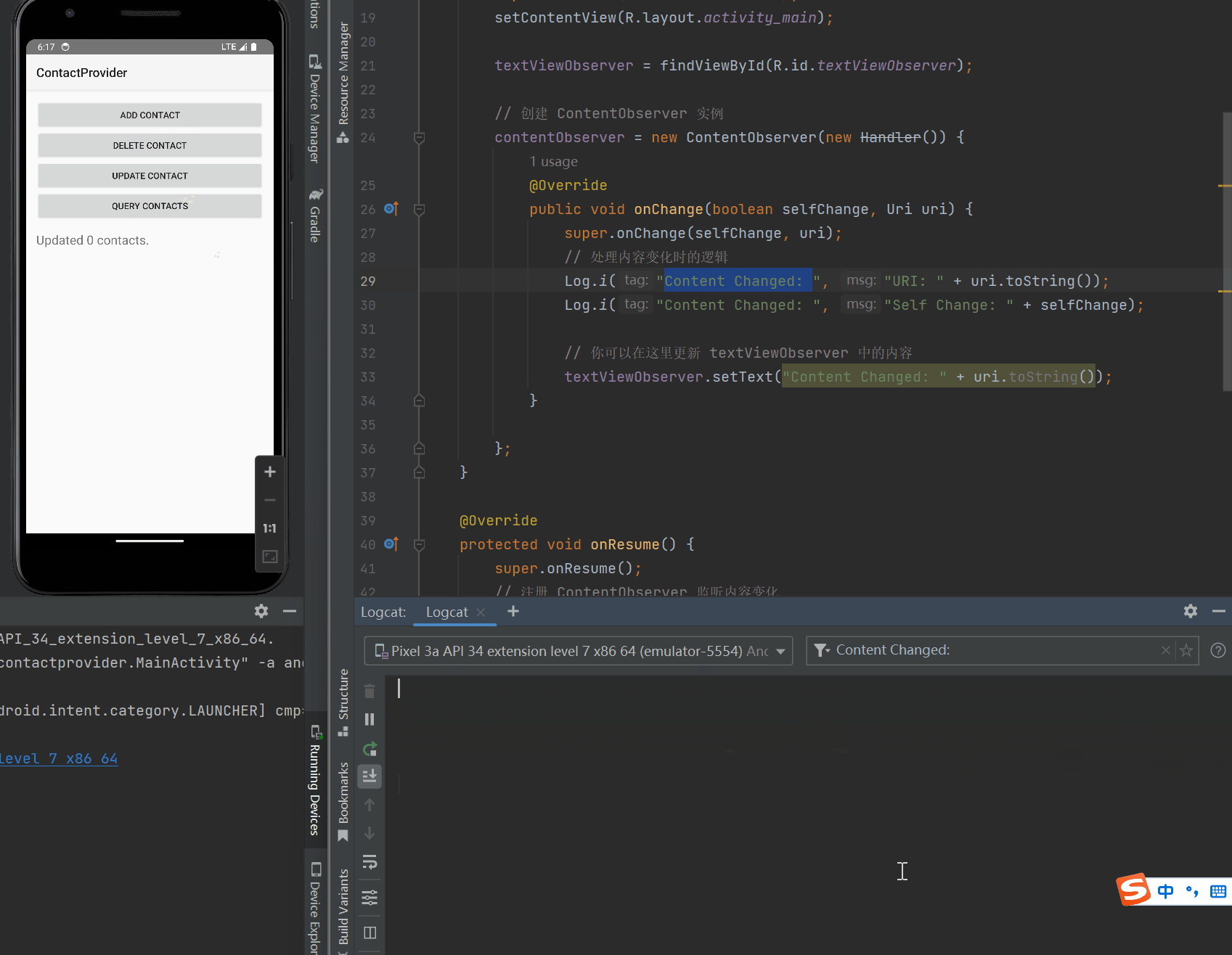
Android 内容提供者和内容观察者:数据共享和实时更新的完美组合
任务要求 一个作为ContentProvider提供联系人数据另一个作为Observer监听联系人数据的变化: 1、创建ContactProvider项目; 2、在ContactProvider项目中用Sqlite数据库实现联系人的读写功能; 3、在ContactProvider项目中通过ContentProvid…...

六、K8S之StatefulSet
StatefulSet 一、概念 和Deployment一样StatefulSet也是中一种可以帮助我们部署和扩展Pod的控制器,使用Deployment时多数时候不需要在意Pod的调度方式。如果需要关心Pod的部署顺序、对应持久化存储或者要求Pod拥有固定的网络标识时,就需要StatefulSet控…...
基于微服务+Java+Spring Cloud开发的建筑工地智慧平台源码 云平台多端项目源码
建筑工地智慧平台源码,施工管理端、项目监管端、数据大屏端、移动APP端全套源码 技术架构:微服务JavaSpring Cloud VueUniApp MySql自主版权实际应用案例演示 建筑工地智慧平台已应用于线上巡查、质量管理、实名制管理、危大工程管理、运渣车管理、绿色…...

微信小程序异常:navigateTo:fail can not navigateTo a tabbar page
场景还原 微信小程序利用路径wx.navigateTo跳转界面时发送异常 跳转代码 showDetail(e){// 获取图片绑定的ID编号let id e.currentTarget.dataset.id;// 指定编号查询 携带参数到详情界面 wx.navigateTo({url: /pages/details/details?id id,})}异常代码 WAServiceMain…...

智慧公厕高精尖技术揭秘,让卫生管理更智能、更舒适
随着科技的飞速发展,智慧公厕正逐渐走进人们的生活。借助物联网、互联网、云计算、大数据、人工智能、自动化控制等技术的应用,智慧公厕将卫生管理提升到一个全新的水平,为公众打造了清洁舒适的使用环境。本文以智慧公厕源头厂家广州中期科技…...

Spring Cloud的革新:服务网格和云原生整合
文章目录 介绍Spring Cloud服务网格的兴起Spring Cloud与Service Mesh的整合1. 服务发现2. 负载均衡3. 故障处理4. 安全性 云原生整合结论 🎉欢迎来到架构设计专栏~Spring Cloud的革新:服务网格和云原生整合 ☆* o(≧▽≦)o *☆嗨~我是IT陈寒ἷ…...
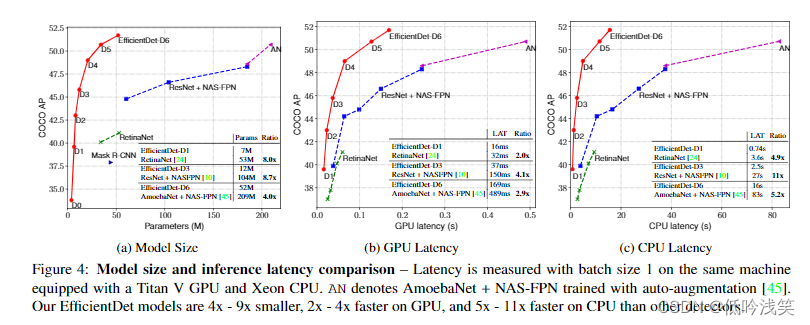
EfficientDet: Scalable and Efficient Object Detection
CVPR2020 V7 Mon, 27 Jul 2020 引用量:243 机构:Google 贡献:1>提出了多尺度融合网络BiFPN 2>对backbone、feature network、box/class prediction network and resolution进行复合放缩,有着不同的…...

【数据结构】二叉树链式存储及遍历
二叉树链式存储及遍历 文章目录 二叉树链式存储及遍历前言实现过程代码实现源代码总结 前言 本文章中的内容参考于王道数据结构考研书,如果你对该部分的内容的记忆有所模糊,可以阅读我的文章再加深印象 实现过程 1.定义二叉树结构体 2.初始化二叉树的根结…...

数字孪生技术:新零售的未来之路
随着科技的不断进步,新零售产业正经历着巨大的变革。数字孪生作为一种新兴技术正在加速这一变革的进程。它不仅为新零售企业带来了更高效的运营方式,还为消费者提供了更个性化、便捷的购物体验。那么,数字孪生技术究竟如何在新零售产业中发挥…...

NIO教程
一,概述 原本的java是基于同步阻塞式的i/o通信(bio) 性能低下,所以出现了nio这种非阻塞式的 二,Java 的I/O演进之路 2.1 i/o模型基本说明 i/o模型:就是用什么样的通道或者说通信模式和架构进行数据的传输和接收&am…...

【MySQL】表的内连和外连
文章目录 一. 内连接二. 外连接1. 左外连接2. 右外连接 一. 内连接 利用where子句对两种表形成的笛卡尔积进行筛选,其实就是内连接的一种方式 另一种方式是inner join select 字段 from 表1 inner join 表2 on 连接条件 and 其他条件现在有如下表 mysql> desc…...

文心一言:文心大模型 4.0 即将发布
本心、输入输出、结果 文章目录 文心一言:文心大模型 4.0 即将发布前言文心 4.0 的成本问题架构文心 4.0 是否可以对标 GPT-4文心4.0 会不会收费弘扬爱国精神文心一言:文心大模型 4.0 即将发布 编辑:简简单单 Online zuozuo 地址:https://blog.csdn.net/qq_15071263 前言 …...
HTML笔记
注释标签:<!-- --> 标题标签:(作用范围依次递减) <h1></h1> <h2></h2> <h3></h3> <h4></h4> <h5></h5> <h6></h6> 段落标签:<p&g…...

design compiler中的drc规则详解
design compiler中的drc规则详解 DRC是什么?DRC分类各个DRC的含义写在最后 DRC是什么? 本文讨论的DRC即是Design Rule Constraint,而不是Design Rule Check,后者是物理端或者后端的一个关键步骤。 DRC分类 DRC为DC中的一个约束大类&#x…...
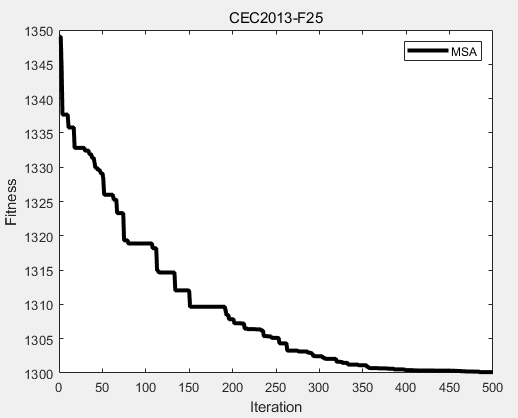
CEC2013(MATLAB):螳螂搜索算法(Mantis Search Algorithm,MSA)求解CEC2013
一、螳螂搜索算法 螳螂搜索算法(Mantis Search Algorithm,MSA)由Mohamed Abdel-Basset等人于2023年提出,该算法模拟螳螂独特的狩猎和性同类相食行为。MSA由三个优化阶段组成,包括寻找猎物(探索)…...

【错误:No package snapd available.】在 CentOS 上启用 snap 并安装 snapd
参考:Install snapd on CentOS using the Snap Store | Snapcraft sudo yum install epel-releasesudo yum install snapd...

Shell命令笔记2
大家好,分享下最近工作中用得比较多的shell命令,希望对大家有帮助。 获取数组长度: ${#array_name[*]}获取脚本相对路径 script_path$(dirname "$0")获取脚本的名字 script_name$(basename "$0")获取脚本的绝对路径 …...
怎么团队合作,协作开发
一、代码托管平台 我是在大一下的一个竞赛中接触到的代码托管平台 那个时候我也算是什么都不会的,不过不得不说这个确实比较重要,对我造成了一些冲击 在我看来,代码托管平台的作用就是在一个中转站(仓库)上存储我们写…...

python 练习--更新
1.判断一个列表中的数值是否全部小于某个数 方法一:利用if函数 (只要列表中有一个数字比大 就可以终止比较) n int(input("请输入需要比较的数字:")) arr1 [1,3,4,5,8] index 0 for i in arr1:if i > n:index 1continue…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

跨链模式:多链互操作架构与性能扩展方案
跨链模式:多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈:模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展(H2Cross架构): 适配层…...

uniapp中使用aixos 报错
问题: 在uniapp中使用aixos,运行后报如下错误: AxiosError: There is no suitable adapter to dispatch the request since : - adapter xhr is not supported by the environment - adapter http is not available in the build 解决方案&…...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...
