【算法1-4】递推与递归-P1002 [NOIP2002 普及组] 过河卒
## 题目描述
棋盘上 A 点有一个过河卒,需要走到目标 B 点。卒行走的规则:可以向下、或者向右。同时在棋盘上 C 点有一个对方的马,该马所在的点和所有跳跃一步可达的点称为对方马的控制点。因此称之为“马拦过河卒”。
棋盘用坐标表示,A 点 (0, 0)、B$点 (n, m),同样马的位置坐标是需要给出的。
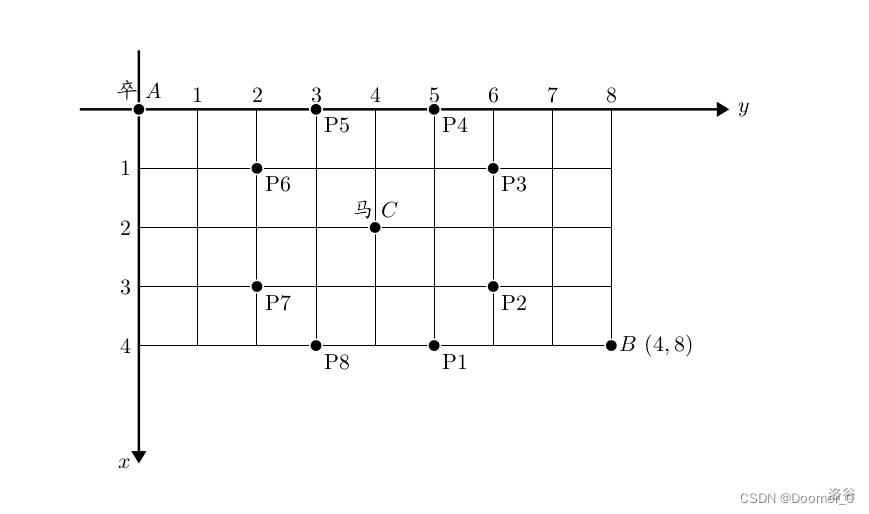
现在要求你计算出卒从 A 点能够到达 B 点的路径的条数,假设马的位置是固定不动的,并不是卒走一步马走一步。
## 输入格式
一行四个正整数,分别表示 B 坐标和马的坐标。
## 输出格式
一个整数,表示所有的路径条数。
## 样例 #1
### 样例输入 #1
6 6 3 3
### 样例输出 #1
6
## 提示
对于 100 % 的数据,1≤n,m≤20,0≤ 马的坐标 ≤20。
分析:
首先要先考虑递推式,并且考虑终止条件
我们对于要到达的b(xb,yb)点,设置一个f(x,y),表示从0,0走到f点的可能数
对于任意的一个点,如果想到达本点,只能从左方和上方移动过来
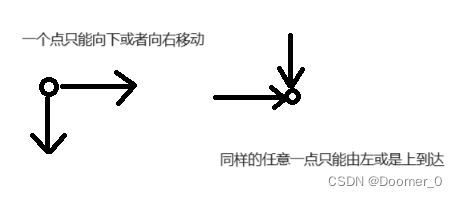
本点坐标如果为x,y则左边点坐标为(x-1,y)上边点坐标为(x,y-1),如果说从左边到本点的可能性为a,从上边到本点的可能性为b,则到达本点总可能性为a+b
因此我们可以得出递推式:f(x,y)=f(x-1,y)+f(x,y-1)
终止条件:
首先第一个点(0,0)到达这个点的可能次数只有1,而(0,y)(x,0)这两条边界的点到达可能同样也只有一种,最后是马以及马脚所在的点,到达的可能性一定为0。
分析完毕,思考解题思路,首先对数据进行输入,用二维数据来模拟棋盘,如果不能走就赋值为1,反之为0。再设置一个二维数组来对f函数即可能到达的可能性进行记录,像是边界直接给赋值1,之后利用递推式依次递推到B点就可以了
一、输入
这边有一个问题,就是如果我的马在1行或者存在于1列,必然会导致,马脚超出数组范围,我们可以建立保护层来方式超出,就是将每个点都+2使得整体往右下偏移,这样最远的马脚也只能到达0行0列,不会超出。
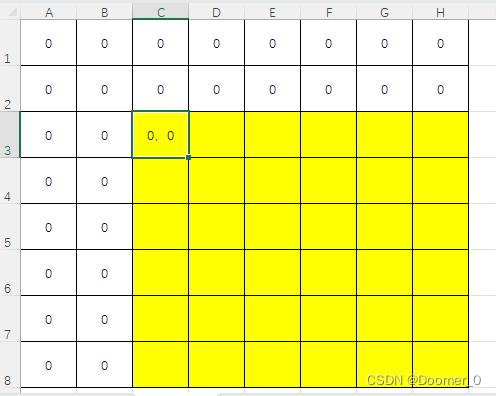
开始定义 马点,B点,以及棋盘和对应点的可能
long long xb,yb,xh,yh;
long long pand[30][30]={0},f[30][30]={0};依次输入之后做偏移
cin>>xb>>yb>>xh>>yh;xb += 2; yb += 2;xh += 2; yh += 2;二、对边界进行赋值
边界到达的可能只有1,所以可以直接赋值
for(int i=2;i<30;i++){f[2][i] = 1;f[i][2] = 1;
}三、马对应的特殊点进行赋值
在地图上的我们对不能到达也就是可能性为0的点进行标注
pand[xh][yh] = 1;pand[xh-2][yh-1] = 1;pand[xh-1][yh-2] = 1;pand[xh+2][yh+1] = 1;pand[xh+1][yh+2] = 1;pand[xh+2][yh-1] = 1;pand[xh+1][yh-2] = 1;pand[xh-2][yh+1] = 1;pand[xh-1][yh+2] = 1;四、递推的计算f(x,y)
在这里通过递推式会遇到问题是0,0点也是现如今的2,2点,因为前面的两点的f函数都为0所以将f1,2或者f2,1赋值为1即可
之后通过递推公式,依次判断,如果遇到马或者马脚,就将可能性为0,代表此路不通直接continue
f[1][2] = 1;for(int i = 2;i<=xb;i++){for(int j = 2;j<=yb;j++){if(pand[i][j]==1){f[i][j] = 0;continue;}f[i][j]= f[i-1][j]+f[i][j-1];}}五、输出
直接将f函数可能性输出即可;
完整代码:
#include <bits/stdc++.h>
using namespace std;
long long xb,yb,xh,yh;
long long pand[30][30]={0},f[30][30]={0};
int main(){cin>>xb>>yb>>xh>>yh;xb += 2; yb += 2;xh += 2; yh += 2;for(int i=2;i<30;i++){f[2][i] = 1;f[i][2] = 1;}pand[xh][yh] = 1;pand[xh-2][yh-1] = 1;pand[xh-1][yh-2] = 1;pand[xh+2][yh+1] = 1;pand[xh+1][yh+2] = 1;pand[xh+2][yh-1] = 1;pand[xh+1][yh-2] = 1;pand[xh-2][yh+1] = 1;pand[xh-1][yh+2] = 1;f[1][2] = 1;for(int i = 2;i<=xb;i++){for(int j = 2;j<=yb;j++){if(pand[i][j]==1){f[i][j] = 0;continue;}f[i][j]= f[i-1][j]+f[i][j-1];}}cout<<f[xb][yb];return 0;
}相关文章:

【算法1-4】递推与递归-P1002 [NOIP2002 普及组] 过河卒
## 题目描述 棋盘上 A 点有一个过河卒,需要走到目标 B 点。卒行走的规则:可以向下、或者向右。同时在棋盘上 C 点有一个对方的马,该马所在的点和所有跳跃一步可达的点称为对方马的控制点。因此称之为“马拦过河卒”。 棋盘用坐标表示&#…...

浅谈压力测试的作用是什么
随着现代应用程序变得越来越复杂,用户的期望也在不断提高,对性能和可靠性的要求变得更加苛刻。在应用程序开发和维护的过程中,压力测试是一项至关重要的活动,它可以帮助发现潜在的问题、评估系统的性能极限,以及确保在…...

互联网Java工程师面试题·Java 总结篇·第一弹
目录 1、面向对象的特征有哪些方面? 2、访问修饰符 public,private,protected,以及不写(默认)时的区别? 3、String 是最基本的数据类型吗? 4、float f3.4;是否正确? 5、short s1 1; s1 s1 1;有错吗…...
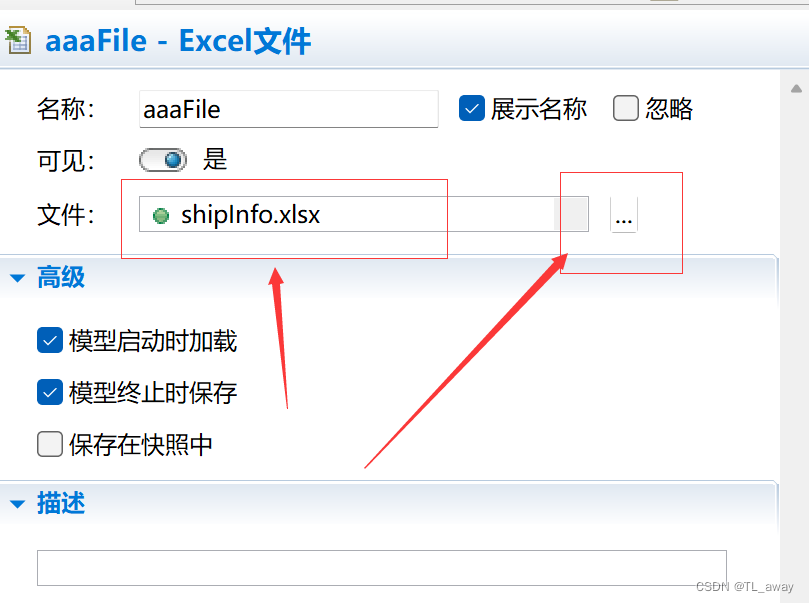
Anylogic 读取和写入Excel文件
1、选择面板-连接-Excel文件,拖入到视图中 然后在excel文件的属性中进行绑定外部excel文件。 绑定完之后,在你需要读取的地方进行写代码, //定义开始读取的行数 //这里设为2,是因为第一行是数据名称 int row12; //读取excel文件信…...
茶百道全链路可观测实战
作者:山猎 茶百道是四川成都的本土茶饮连锁品牌,创立于 2008 年 。经过 15 年的发展,茶百道已成为餐饮标杆品牌,全国门店超 7000 家,遍布全国 31 个省市,实现中国大陆所有省份及各线级城市的全覆盖。2021 …...

Java-JDBC
JDBC JDBC英文名为:Java Data Base Connectivity(Java数据库连接),官方解释它是Java编程语言和广泛的数据库之间独立于数据库的连接标准的Java API 根本上说JDBC是一种规范,它提供的接口,一套完整的,允许便捷式访问底…...

【ROS】Nav2源码之nav2_planner详解
【ROS】郭老二博文之:ROS目录 1、简述 nav2_planner是路径规划器,把起始位置、姿势的信息输入nav2_planner模块,将会生成可行路径。 nav2_planner路径规划器和nav2_controller控制器相似,也使用插件的形式加载不同的路径规划器。 常用的路径规划器插件有: 1)NavFn Plan…...

mysql报SQLSTATE[22007]的错误的一个原因
最近在修改一个程序,打算将$video这个参数保存到数据库。修改的过程中出现错误。导致该程序不能发布新文章。在程序的一个db.php程序文件里使用var_dump($input, $stmt) ; 语句看到了错误信息,并找到了错误原因。信息里包含的错误代码是: SQ…...

Python —— UI自动化之 三大等待与三大切换
1、三大等待 1、硬性等待 1、概述 硬性等待也可以称之为强制等待,写法如下: time.sleep() 优点:使用简单 缺点:等待时间把握不准,容易造成时间浪费或者等待时间不足 2、实战 from time import sleep from sele…...
初识容器Docker
目前使用 Docker 基本上有两个选择:Docker Desktop和Docker Engine。Docker Desktop 是专门针对个人使用而设计的,支持 Mac 和 Windows 快速安装,具有直观的图形界面,还集成了许多周边工具,方便易用。 不是太推荐使用D…...
pikachu靶场搭建及通关
一、靶场搭建 下载工具:phpstudy Pikachu靶机下载地址: https://github.com/zhuifengshaonianhanlu/pikachu 下载后解压缩并放入如下文件夹(网站根目录) 建议修改文件名称为 pikachu 修改配置文件(mysql 用户名&…...

选择排序(学习笔记)
选择排序 选择排序的基本思想是冒泡排序,记录当前位置i和最小值k的位置,使用一个变量j往后寻找。 每一轮找到最小值后与第一个元素进行交换,以此类推。 不使用辅助变量交换两个元素的值方法 package com.company.sort;import java.util.Ra…...

PCL 生成球形点云
目录 一、算法原理二、代码实现三、结果展示四、参考链接一、算法原理 生成球体点云的方法有很多种,Marsaglia于1972年提出了一个简单易行的实现方法,它从(-1,1)上的独立均匀分布中选取 x 1 x_1 x...

Flutter 剪裁(Clip)
🔥 ClipOval 🔥 子组件为正方形时剪裁成内贴圆形;为矩形时,剪裁成内贴椭圆 裁剪纯色背景 ClipOval(child: Container(width: 300.w,height: 300.w,decoration: const BoxDecoration(color: Colors.red),),), 裁剪背景图片 裁剪前…...

嵌入式C语言自我修养《GNU C编译器扩展语法》学习笔记
目录 一、C语言标准和编译器 二、指定初始化 三、宏构造“利器”:语句表达式 四、typeof与container_of宏 五、零长度数组 六、属性声明:section 七、属性声明:aligned 一、C语言标准和编译器 C语言标准的发展过程: ●…...

密码学二: md5 网站服务器与用户通信过程 ca原理 签名原理 Flame 病毒原理
md5被破解? MD5(Message Digest Algorithm 5)是一个较早的哈希函数,但由于其弱点和漏洞,它已经被认为不再适合用于安全性要求较高的应用。MD5的一些安全性问题包括: 碰撞攻击: MD5已经被证明容易受到碰撞攻…...
Zend Framework 3.1.3 gadget chain
前言 在推特上的PT SWARM账号发布了一条消息。 一个名为Zend Framework的php框架出现了新的gadget chain,可导致RCE。笔者尝试复现,但失败了。所幸,我基于此链,发现在这个框架的最新版本中的另一条链。 复现过程 这里使用vscod…...

互联网Java工程师面试题·Java 并发编程篇·第四弹
目录 39、volatile 有什么用?能否用一句话说明下 volatile 的应用场景? 40、为什么代码会重排序? 41、在 java 中 wait 和 sleep 方法的不同? 42、用 Java 实现阻塞队列 43、一个线程运行时发生异常会怎样? 44、…...

3、Linux下安装
以下操作仅限于rh系列:支持rpm/yum安装方式,不支持deb/apt安装方式。 以下操作仅限于rh系列:支持rpm/yum安装方式,不支持 deb/apt安装方式。 1、在线下载安装包: wget https://downloads.mysql.com/archives/get/p/23/file/ m…...
Zookeeper【Curator客户端Java版】从0到1——万字学习笔记
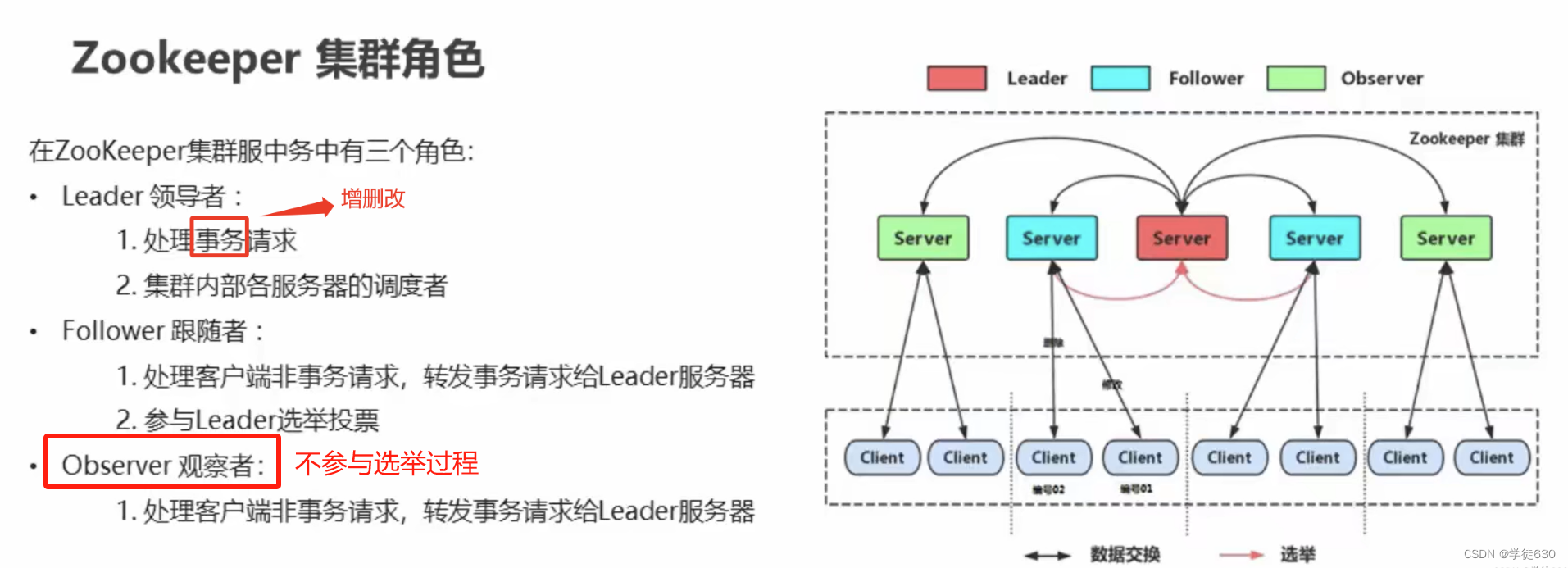
目录 初识Zookeeper Zookeeper作用 维护配置信息 分布式锁服务 集群管理 生产分布式唯一ID Zookeeper的设计目标 Zookeeper 工作机制 数据模型 ZooKeeper 命令操作 服务端常用命令 客户端常用命令 ZooKeeper JavaAPI操作 Curator 介绍 Curator API 常用操作 导入依赖 建立连接 …...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...
