数据结构和算法——树结构
二叉树
又叫二叉排序树。
节点是数量为,,n为层数。
满二叉树:所有的叶子节点都在最后一层。
完全二叉树:如果所有叶子节点都在最后一层和倒数第二层,而且每个叶子节点都有左右子节点。
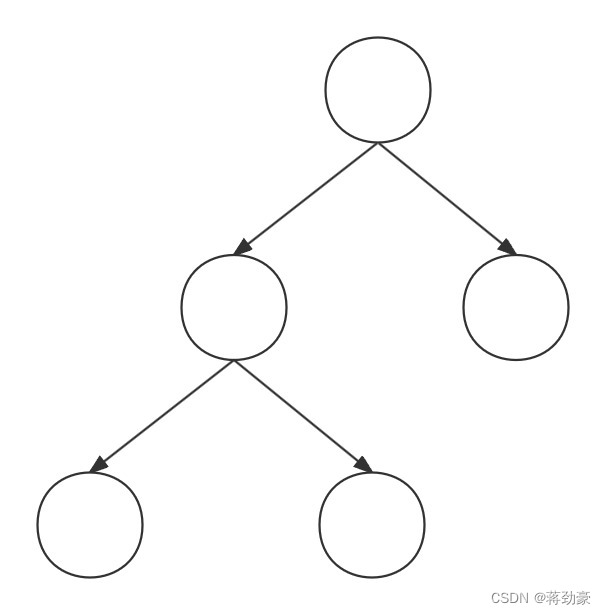
前序遍历
1、先输出当前节点(初始是root节点)。
2、如果左子节点不为空,则递归继续前序遍历。
3、如果右子节点不为空,则递归继续前序遍历。
class HeroNode {private int no;private String name;private HeroNode left, right;
} public HeroNode preOrderSearch(int no) {if (this.no == no) {return this;}HeroNode resNode;if (this.left != null) {resNode = this.left.preOrderSearch(no);if (resNode != null) {return resNode;}}if (this.right != null) {resNode = this.right.preOrderSearch(no);if (resNode != null) {return resNode;}}return null;}中序遍历
1、如果当前节点的左子节点不为空,则递归中序遍历。
2、输出当前节点。
3、如果当前节点的右子节点不为空,则递归中序遍历。
public HeroNode infixOrderSearch(int no) {HeroNode resNode;if (this.left != null) {resNode = this.left.infixOrderSearch(no);if (resNode != null) {return resNode;}}if (this.no == no) {return this;}if (this.right != null) {resNode = this.right.infixOrderSearch(no);if (resNode != null) {return resNode;}}return null;}后序遍历
1、如果当前节点的左子节点不为空,则递归后序遍历。
2、如果当前节点的右子节点不为空,则递归后序遍历。
3、输出当前节点。
public HeroNode postOrderSearch(int no) {HeroNode resNode;if (this.left != null) {resNode = this.left.postOrderSearch(no);if (resNode != null) {return resNode;}}if (this.right != null) {resNode = this.right.postOrderSearch(no);if (resNode != null) {return resNode;}}if (this.no == no) {return this;}return null;}二叉树节点的删除,如果是中间节点,则整个中间节点都删除。
public void delNode(int no) {if (this.no == no) {return;}if (this.left != null) {if (this.left.no == no) {this.left = null;} else {this.left.delNode(no);}}if (this.right != null) {if (this.right.no == no) {this.right = null;} else {this.right.delNode(no);}}}顺序存储二叉树
顺序二叉树通常是完全二叉树。
第n(n是下标)个元素的左子节点为 2 * n + 1
第n个元素的右子节点为 2 * n + 2
第n个元素的父节点为 (n - 1) / 2

堆排序用到顺序存储二叉树的结构。
线索化二叉树
充分的利用到了叶子节点的空指针。
class HeroNode {private int no;private String name;private HeroNode left, right;private int leftType; // 0 指向的是左子树 1指向前驱节点private int rightType; // 0 指向的是右子树 1指向后继节点
}对线索二叉树进行中序线索化的方法
public void threadedNodes(HeroNode node) {if (node == null) {return;}threadedNodes(node.getLeft()); // 先线索化左子树// 再线索化当前节点if (node.getLeft() == null) { // 前驱node.setLeft(pre);node.setLeftType(1);}if (pre != null && pre.getRight() == null) { // 后继pre.setRight(node);pre.setRightType(1);}pre = node;threadedNodes(node.getRight()); // 最后线索化右子树}线索化二叉树的中序遍历
class ThreadedBinaryTree {private HeroNode root;private HeroNode pre = null; // 指向前驱节点public void threadedList() {HeroNode node = root;while (node != null) {while (node.getLeftType() == 0) { // 到左下角node = node.getLeft();}System.out.println(node);while (node.getRightType() == 1) {node = node.getRight();System.out.println(node);}node = node.getRight();}}
}平衡二叉树
又叫AVL树。
B树
B+树
B*树
相关文章:

数据结构和算法——树结构
二叉树 又叫二叉排序树。 节点是数量为,,n为层数。 满二叉树:所有的叶子节点都在最后一层。 完全二叉树:如果所有叶子节点都在最后一层和倒数第二层,而且每个叶子节点都有左右子节点。 完全二叉树 前序遍历 1、先输…...

【Java】Integer包装类
Integer:对基本数据类型 int 实现包装 方法名称说明public Integer(int value)根据 int 值创建 Integer 对象(JDK9以后过时)public integer(String s)根据 String 值创建 Integer 对象…...
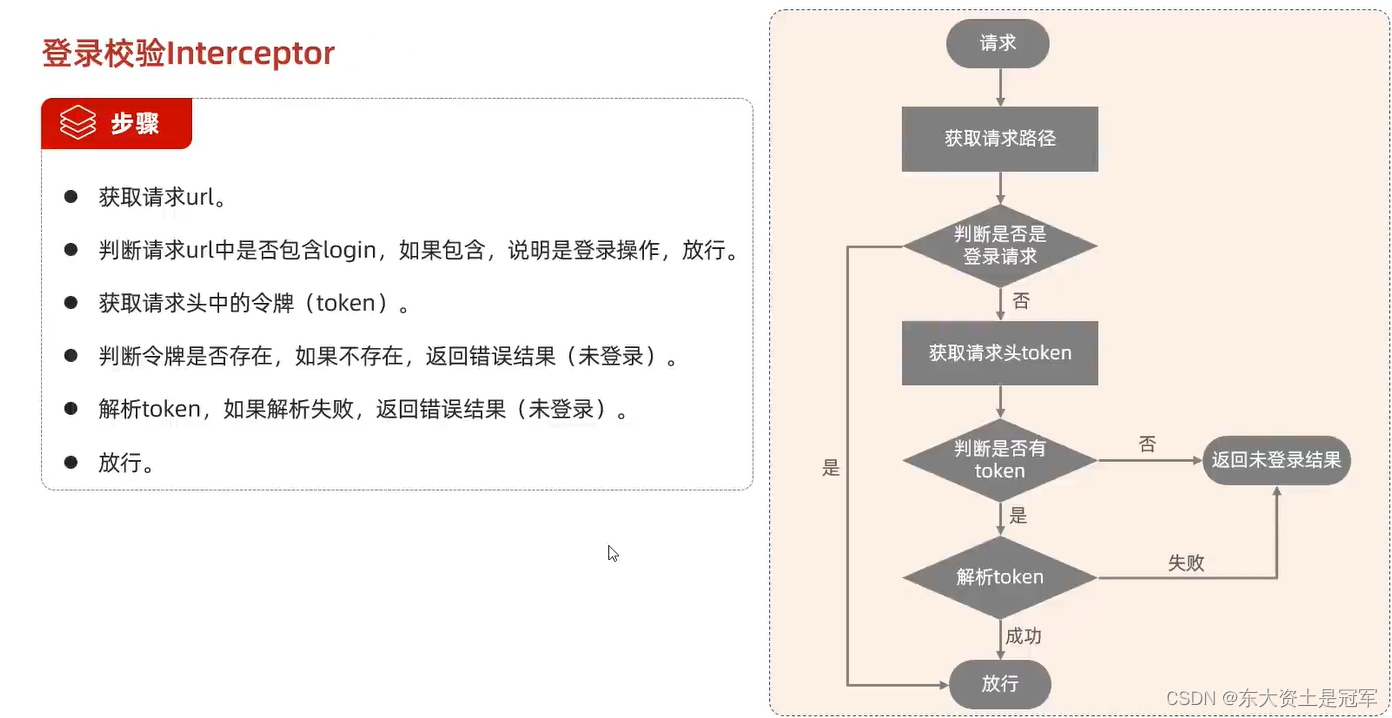
Web后端开发登录校验及JWT令牌,过滤器,拦截器详解
如果用户名正确则成功进入 登录功能 代码 Controller Service Mapper 结果 若登录成功结果如下: 如果登录失败,结果如下 登录校验 为什么需要登录校验 有时再未登录情况下, 我们也可以直接访问部门管理, 员工管理等功能 因此我们需要一个登录校验操作, 只有确认用户登录…...

大语言模型迎来重大突破!找到解释神经网络行为方法
前不久,获得亚马逊40亿美元投资的ChatGPT主要竞争对手Anthropic在官网公布了一篇名为《朝向单义性:通过词典学习分解语言模型》的论文,公布了解释经网络行为的方法。 由于神经网络是基于海量数据训练而成,其开发的AI模型可以生成…...

zabbix内置宏、自动发现与注册
一、zabbix内置宏 1、概念: 在Zabbix中,内置宏是一种特殊的变量,通常用在 Trigger 名称和表达式中,引用有关监控对象的信息。 2、种类: {HOST.NAME} 主机名 {HOST.IP} 主机 IP 地址 {TRIGGER.DESCRIPTION} 触…...

Oracle与Mysql语法区别
database 一、数据类型二、update..select语句三、upsert语句四、常见函数五、自动更新列时间戳一、数据类型 OracleMysqlnumberint/decimal变长字符:varchar2varchardatedatetime/timestampinttinyint/smallint/mediumint/int/bigint二、update…select语句 Oracle update t…...

Jetpack:008-Icon与Image
文章目录 1. 概念介绍2. 使用方法2.1 Icon2.2 Image 3. 示例代码4. 内容总结 我们在上一章回中介绍了Jetpack中与Button相关的内容,本章回中主要I con与Image。闲话休提,让我们一起Talk Android Jetpack吧! 1. 概念介绍 我们在本章回中介绍…...
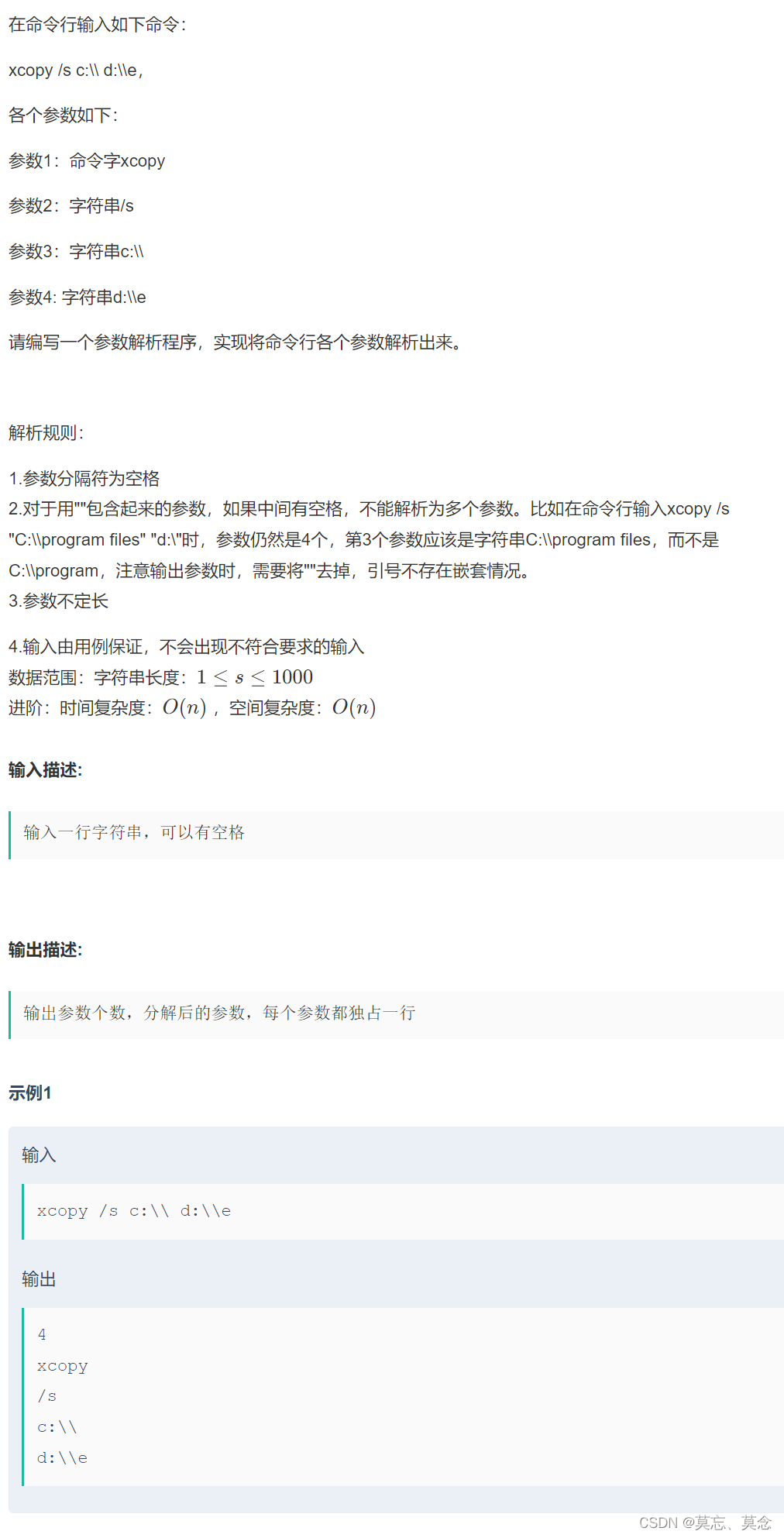
参数解析(牛客)
目录 一、题目 二、代码 一、题目 二、代码 #include <iostream> #include <vector> using namespace std;int main() {string s;getline(cin, s);int i 0;vector<string>ret;while (i < s.size()){if (s[i] )//遇到空格直接跳过{i;}else if (s[i] …...
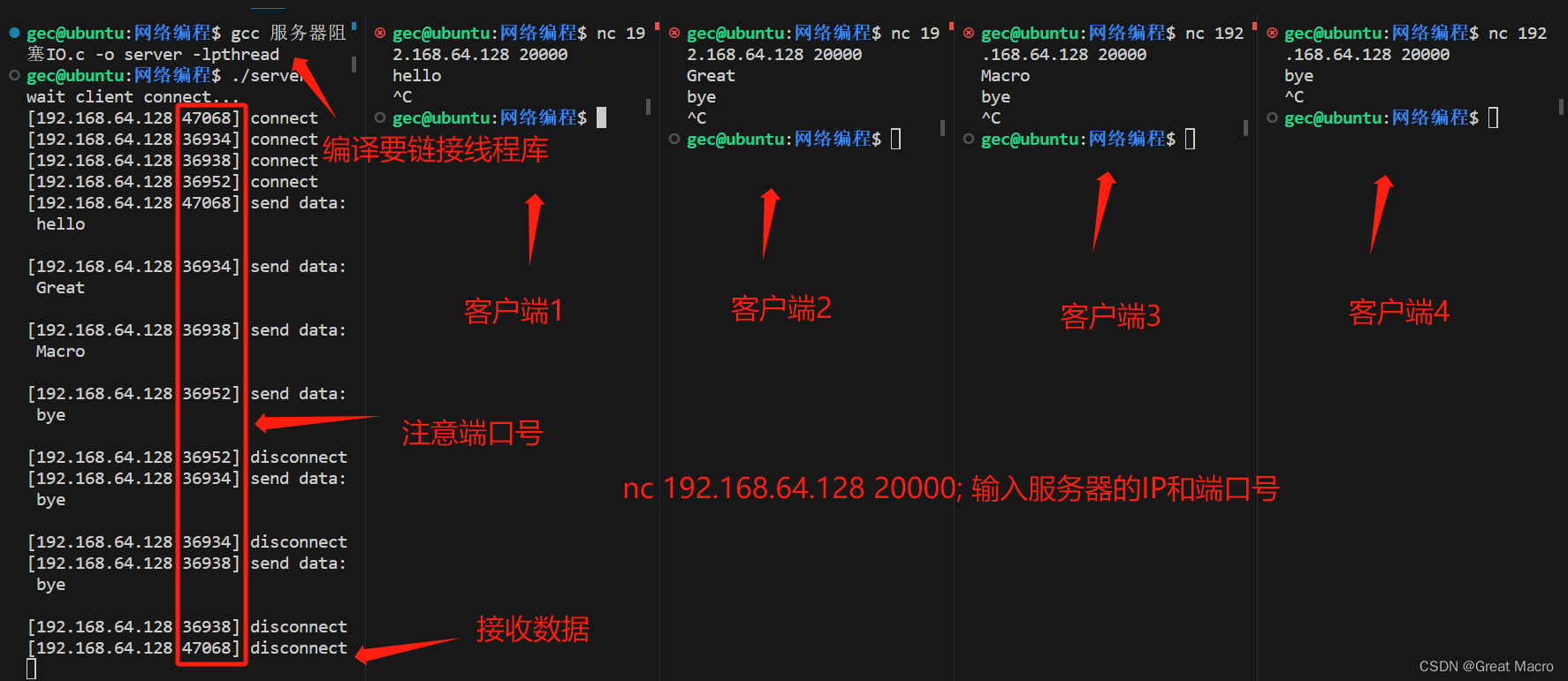
Linux网络编程系列之服务器编程——阻塞IO模型
Linux网络编程系列 (够吃,管饱) 1、Linux网络编程系列之网络编程基础 2、Linux网络编程系列之TCP协议编程 3、Linux网络编程系列之UDP协议编程 4、Linux网络编程系列之UDP广播 5、Linux网络编程系列之UDP组播 6、Linux网络编程系列之服务器编…...
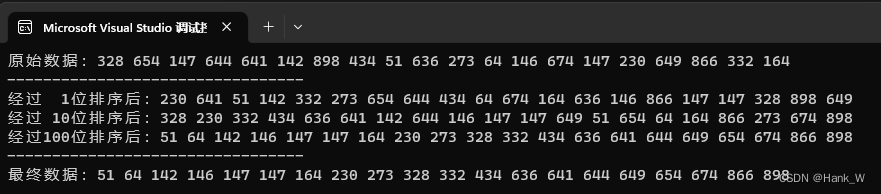
排序算法-基数排序法(RadixSort)
排序算法-基数排序法(RadixSort) 1、说明 基数排序法与我们之前讨论的排序法不太一样,并不需要进行元素之间的比较操作,而是属于一种分配模式排序方式。 基数排序法比较的方向可分为最高位优先(Most Significant Di…...

nginx绑定tomcat与tomcat联合使用的配置(nginx反向代理tomcat的配置说明)
nginx反向代理tomcat通信配置 (内容来自网上,注解部分才是原创) 切记: url的意思就是 unifed resource location 统一资源定位 其中location就是定位的意思 所以上文中的location就有 对应匹配的 url 标识的资源的相关配置之…...
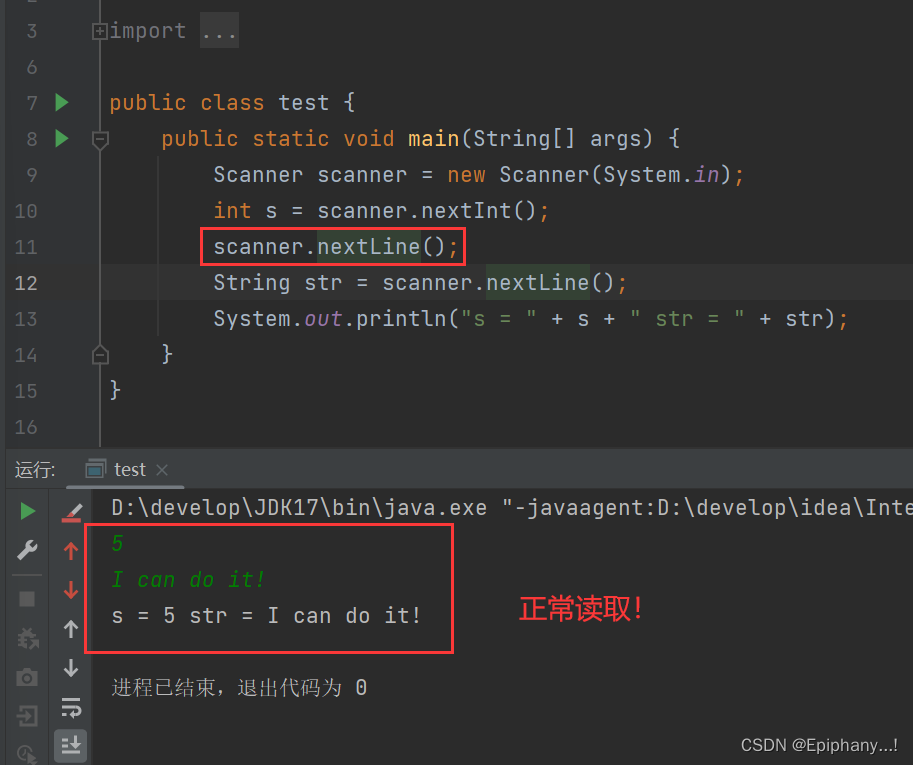
【Java】nextInt()后面紧接nextLine()读取不到数据/InputMismatchException异常的解决方案
错误如下: 有时候还会抛出InputMismatchException异常 看!我只输入了一个5,并没有给str赋值,它就已经将结果打印出来了!这就意味着,str是读取到了数据的,只不过这个数据并不是我们想要的输入的…...
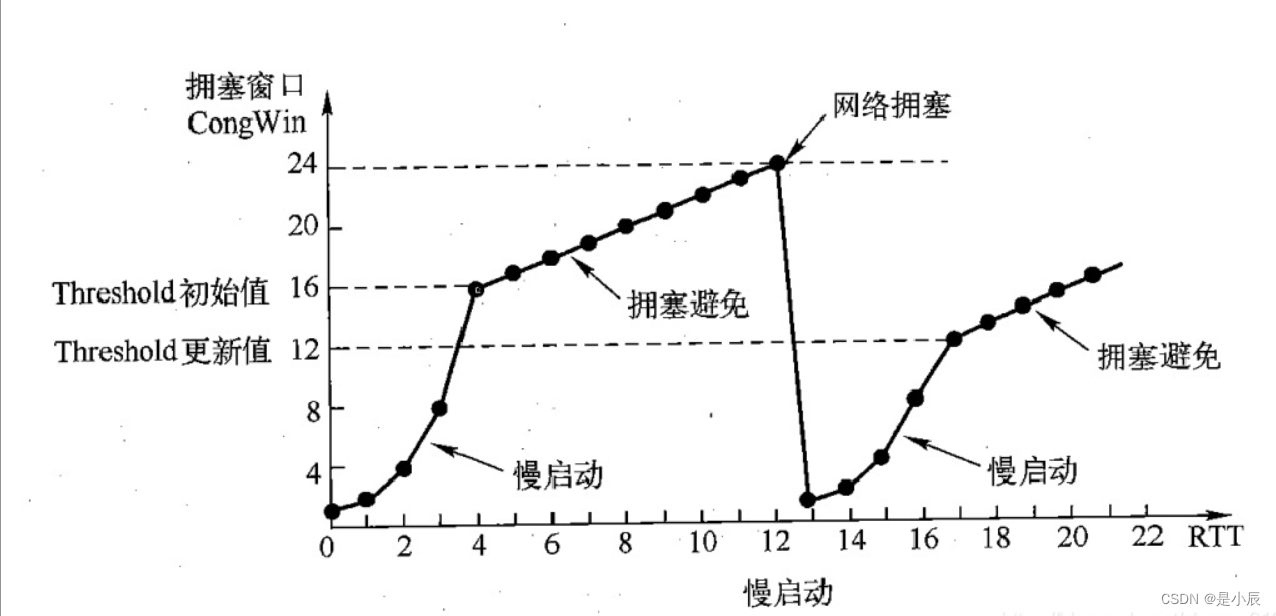
【传输层协议】UDP/TCP结构特点与原理(详解)
文章目录 1. UDP1.1 UDP结构1.2 UDP特点1. 无连接2. 不可靠3. 面向数据报4. 缓冲区5. 大小受限6. 无序性 2. TCP2.1 TCP结构2.2 TCP特点1. 有连接2. 可靠性3. 面向字节流4. 拥塞控制5. 头部开销 2.3 TCP原理1. 确认应答(安全机制)2. 超时重传(…...

哪种网站适合物理服务器
哪种网站适合物理服务器 看到独立服务器这一词语,相信大家脑海立马就浮现出了它的种种优势,但是有优势就伴随着也有一定的弊端,比如说它的空间大、特殊的的组件配置,权限配置等,但是成本却非常的高,那么我…...

uni-app集成使用SQLite
一、打开uni-app中SQLite 二、封装sqlite.js module.exports {dbName: chat, // 数据库名称dbPath: _doc/chat.db, // 数据库地址,推荐以下划线为开头 _doc/xxx.db/*** Description: 创建数据库 或 有该数据库就打开* author: ZXL* createTime: 2023-10-12 09:23:10* Copyr…...

Qt不能安装自己想要的版本,如Qt 5.15.2
使用在线安装工具安装Qt5.15.2时,发现没有Qt 5的相关版本,只有Qt 6的版本,这时选择右边的Archive,再点击筛选,这时就会出现之前的Qt版本。...
学信息系统项目管理师第4版系列28_组织级项目管理和量化项目管理
1. OPM 1.1. 旨在确保组织开展正确项目并合适地分配关键资源 1.1.1. 有助于确保组织的各个层级都了解组织的战略愿景、实现愿景的措施、组织目标以及可交付成果 1.2. 业务评估是建立OPM框架的必要组件 1.3. OPM3 是组织级项目管理成熟度模型,可用于评估组织项目…...

Bean实例化的三级缓存
在Spring框架中,Bean实例化的三级缓存(三级缓存也称为三级缓存机制)是用于缓存Bean定义的一种机制,用于管理和加速Spring容器中Bean的创建和初始化过程。三级缓存包括了singletonObjects、earlySingletonObjects 和 singletonFact…...

Jenkins+Gitlab+Docker(Dockerfile)部署
Docker部署运行 上一篇内容中使用Jenkins(运行服务器)Gitlab(代码存储库)Webhook(网络钩子)的方式部署运行我们的项目。需要我们在服务器上做好很多相关的环境配置及依赖。 那么假如有这样一个场景:需要把不同技术栈的项目部署到同一台服务器上运行。比如PH…...
)
Web前端-Vue2+Vue3基础入门到实战项目-Day4(组件的三大组成部分, 组件通信, 案例-组件版小黑记事本, 进阶语法)
Web前端-Vue2Vue3基础入门到实战项目-Day4 组件的三大组成部分(结构/样式/逻辑)scoped样式冲突data是一个函数 组件通信组件通信语法父传子子传父props详解什么是propsprops检验props与data的区别 非父子(扩展)事件总线 (event bus)provide - inject 案例 - 小黑记事本(组件版)…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

EtherNet/IP转DeviceNet协议网关详解
一,设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络,本网关连接到EtherNet/IP总线中做为从站使用,连接到DeviceNet总线中做为从站使用。 在自动…...

鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南
1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发,使用DevEco Studio作为开发工具,采用Java语言实现,包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...
与常用工具深度洞察App瓶颈)
iOS性能调优实战:借助克魔(KeyMob)与常用工具深度洞察App瓶颈
在日常iOS开发过程中,性能问题往往是最令人头疼的一类Bug。尤其是在App上线前的压测阶段或是处理用户反馈的高发期,开发者往往需要面对卡顿、崩溃、能耗异常、日志混乱等一系列问题。这些问题表面上看似偶发,但背后往往隐藏着系统资源调度不当…...

AirSim/Cosys-AirSim 游戏开发(四)外部固定位置监控相机
这个博客介绍了如何通过 settings.json 文件添加一个无人机外的 固定位置监控相机,因为在使用过程中发现 Airsim 对外部监控相机的描述模糊,而 Cosys-Airsim 在官方文档中没有提供外部监控相机设置,最后在源码示例中找到了,所以感…...

【C++进阶篇】智能指针
C内存管理终极指南:智能指针从入门到源码剖析 一. 智能指针1.1 auto_ptr1.2 unique_ptr1.3 shared_ptr1.4 make_shared 二. 原理三. shared_ptr循环引用问题三. 线程安全问题四. 内存泄漏4.1 什么是内存泄漏4.2 危害4.3 避免内存泄漏 五. 最后 一. 智能指针 智能指…...
