【排序算法】详解直接插入排序和希尔排序原理及其性能分析
文章目录
- 插入排序
- 算法原理
- 细节分析
- 代码实现
- 复杂度分析:
- 稳定性分析:
- 与冒泡排序的对比
- 希尔排序
- 算法原理
- 细节分析
- 代码实现
- 复杂度分析
- 稳定性分析
- 总结对比
插入排序
算法原理
插入排序又或者说直接插入排序,是一种和冒泡排序类似的并且比较简单的排序方法,
基本思想是:把待排序的记录按其关键码值的大小逐个插入到一个已经排好序的有序序列中,直到所有的记录插入完为止,得到一个新的有序序列 。就像大家平时打扑克牌一样.
类似于摸牌然后将其按照顺序排列。每次摸到一张牌后,根据其点数从左到右插入到确切位置。
动图演示如下
细节分析
用for循环控制,从最左侧的元素开始,用它右侧的元素进行依次比较(将这个右侧的元素设置为tmp),并挪动位置,最后将其插入合适的位置
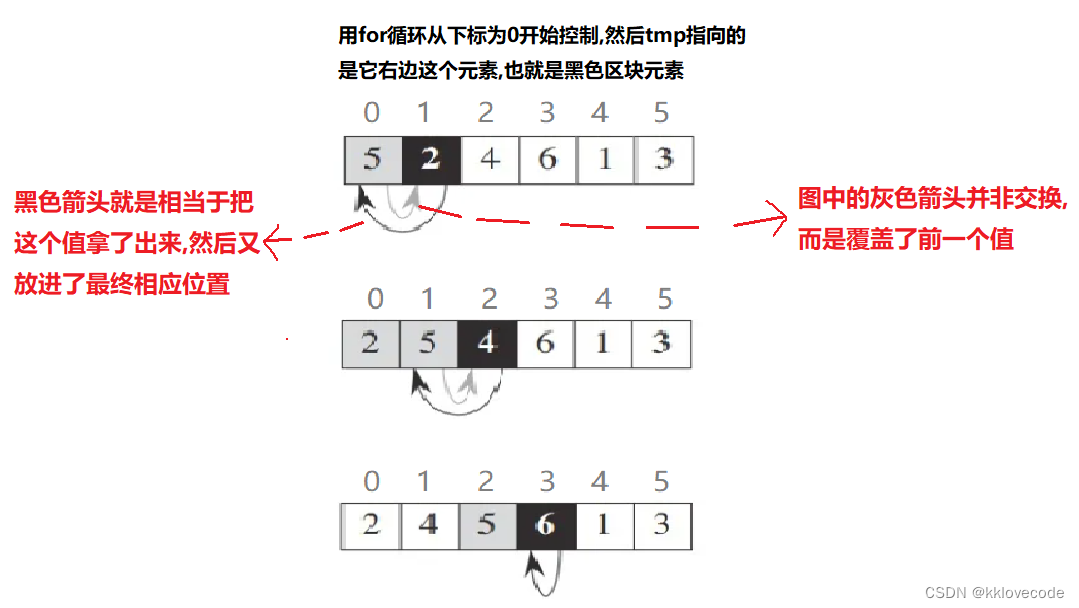
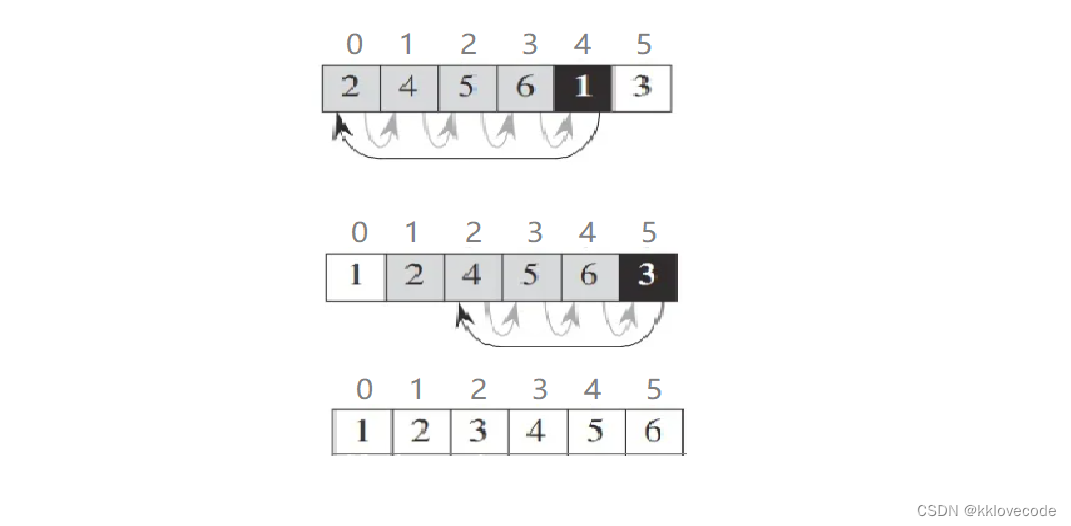
注意:看似图中是在用黑色阴影这个元素在与其前面的做交换,其实并没有,真正原理应该是把黑色阴影里面的元素拿出来(赋值给了tmp),然后与前面的进行比较,有合适的即进行覆盖,但是由于黑色阴影的值已经拿了出来(也就是tmp里面的值),所以在比较之后便可以覆盖,不会丢失这个值
代码实现
int sortArray(int* nums, int numsSize)
{for(int i = 0;i<numsSize-1;i++){int pointer = i;int tmp = nums[i+1];while(pointer>=0){if(nums[pointer]>tmp){nums[pointer+1] = nums[pointer];pointer--;}else{break;}}nums[pointer+1] = tmp;}
}
再配上一张代码细节的具体分析

复杂度分析:
时间复杂度
(1) 最好情况:序列已经是升序排列,在这种情况下,如果原序列本身就已经是排好了序的,那么每一趟排序只需要比较一次而不需要任何移动。此时一共需要 n-1 次比较,也就是
O(N)
(2) 最坏情况:如果原序列本身就是逆序的,那么第 i(1 ≤ i ≤ n-1)趟排序需要比较 i 次、移动 i+2 次(包括将待排序元素移动到tmp变量中和从tmp变量中移动到最终位置上)。此时,一共需要1+2+3+…+(n-1) = n(n-1)/2,所以O(N^2)
空间复杂度
直接插入排序只需要一个额外的tmp变量,所以它的空间复杂度为
O(1)
稳定性分析:
因为插入排序是只有当前元素比另外一个元素大的时候才会交换,所以相同元素的前后相对位置并不会改变,所以排序稳定
与冒泡排序的对比
若具体看冒泡排序,请看这篇文章–>冒泡排序文章戳此处
下图代表前面的元素全部有序,就最后两个无序

希尔排序
算法原理
希尔排序是希尔排序由唐纳德·希尔(Donald Shell)发明并于1959年公布,在直接插入排序算法的基础上进行改进而来的,从上面的直接插入排序我们可以看出,当原序列的长度很小时,即便它的所有元素都是无序的,此时进行的元素比较和移动的次数还是很少。所以希尔排序正是利用这点,它首先将待排序的原序列划分成很多小的序列,称为子序列。然后对这些子序列进行直接插入排序,因为每个子序列中的元素变少了,所以效率也提高了.
说简单就两点:1.先进行预排序2.直接插入排序
细节分析
具体步骤如图:
原始数组,我们设定颜色相同为一组

初始分gap组,gap = n / 2 = 5,也就是分了5组,[8,3][9,5][1,4][7,6][2,0]
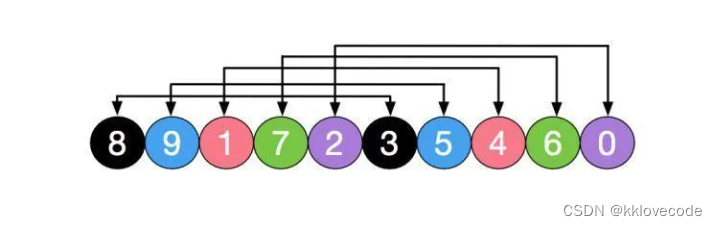
五组分别进行插入排序,此时8,9,7这种大元素被排到前面,如下图,然后再缩小gap,分为2组,[3,1,0,9,7][5,6,8,4,2]
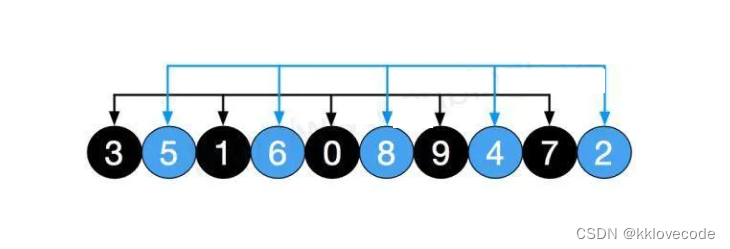
对以上两组再进行直接插入排序,结果如下,可以看出数组更加接近有序,再将gap除以2,也就是gap =1, 此时就变成了直接插入排序,此时整个数组为1组[0,2,1,4,3,5,7,6,9,8]
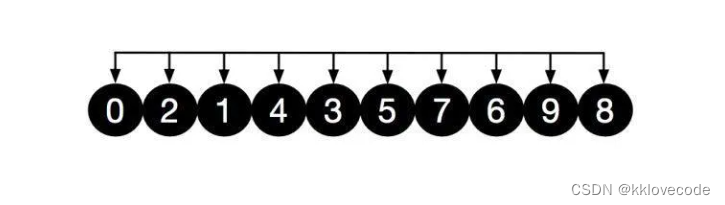
此时再进行微调,便达到了有序

由此可以看出,在前面gap不等于1时,前面几组调整都是预排序,而这种预排序完成之后就已经接近有序了,而上面在直接插入排序中我们也说到了,在顺序好的情况下,时间复杂度为O(N),而这里接近有序,时间复杂度也可以大概看作O(N),大大节省了时间,这也是希尔排序的主要作用和意义
代码实现
void sortArray(int* nums, int numsSize)
{int gap = 6;while(gap>1){gap=gap/3+1; //上图是gap = gap/2;两者都行,但官方是更推荐gap=gap/3+1for(int i = 0;i<numsSize-gap;i++){int pointer = i;int tmp = nums[i+gap];while(pointer>=0){if(nums[pointer]>tmp){nums[pointer+gap] = nums[pointer];pointer -= gap;}else{break;}}nums[pointer+gap] = tmp;}}
}
通过上面你能发现希尔排序的代码无非就是在直接插入排序的基础之上多了一个while循环来控制gap分组
复杂度分析
时间复杂度
希尔排序的时间复杂度分析十分困难,希尔排序的平均时间复杂度和执行它所选择的gap分组有关,这就要设计一些复杂的数学问题,在Knuth编著的《计算机程序设计技巧》第三卷中的大量分析得出,时间复杂度大概在
O(n^(1.3)),即n的1.3次方。
空间复杂度
从我们以上的实现代码中可以看出,希尔排序只需要几个固定的额外存储空间,分别用于存储变量,这和它的待排序序列的大小无关。所以,它的空间复杂度为
O(1)。
稳定性分析
由于多次插入排序,我们知道一次插入排序是稳定的,不会改变相同元素的相对顺序,但在不同的插入排序过程中,相同的元素可能在各自的插入排序中移动,最后其稳定性就会被打乱,所以希尔排序是不稳定的。
总结对比
希尔排序和直接插入排序直接有着很强的关联性,希尔排序就是直接插入排序的加强版,利用预排序进行优化,提高排序的效率.
总的来说,直接插入排序适用于小规模或基本有序的元素,具有简单易懂的实现方法和稳定的排序性质;希尔排序适用于中大型规模的元素,通过预处理和分组插入排序的方式,提高了排序的效率。选择使用哪种算法取决于具体的需求和数据特征。
相关文章:

【排序算法】详解直接插入排序和希尔排序原理及其性能分析
文章目录 插入排序算法原理细节分析代码实现复杂度分析:稳定性分析:与冒泡排序的对比 希尔排序算法原理细节分析代码实现复杂度分析稳定性分析 总结对比 插入排序 算法原理 插入排序又或者说直接插入排序,是一种和冒泡排序类似的并且比较简单的排序方法, 基本思想…...

JDK1.8对HashMap的优化、以及通过源码解析1,8扩容机制
JDK 1.8 对 HashMap 进行了一些优化,主要包括以下几个方面的改进: 红黑树:在 JDK 1.8 中,当哈希碰撞(多个键映射到同一个桶)达到一定程度时,HashMap 会将链表转化为红黑树,以提高查找…...

Linux串口断帧处理
报文格式 1 Byte 4 Byte N Byte 4 Byte 1 Byte 0x02 报文长度 报文 CRC16 0x03 1. 每条报文以 STX(0x02)起始符开始,以 ETX(0x03)终止符结束。 2. 报文正文长度采用 4 字节的 10 进制字符串标识,如报文正…...
springboot集成kafka
1、引入依赖 <dependency><groupId>org.springframework.kafka</groupId><artifactId>spring-kafka</artifactId><version>2.8.6</version></dependency> 2、配置 server:port: 9099 spring:kafka:bootstrap-servers: 192.1…...

近期总结2023.10.16
规律 1.两数相减,相加的最大,最小值 2.由最初的状态递推 3.无强制顺序,排序,不能排序,则与顺序有关 4.对于一段等差数列,不用一段一段的算局部整体,可以从整体一步步加差值 5.需要从一段式子推到结果困难&…...

【EI会议征稿】第二届可再生能源与电气科技国际学术会议(ICREET 2023)
第二届可再生能源与电气科技国际学术会议(ICREET 2023) 2023 2nd International Conference on Renewable Energy and Electrical Technology 2020年中国可再生能源发电规模显著扩大,风力和太阳能发电均呈迅速增长趋势。中国大力推进能源低碳化,减少温…...

让ChatGPT等模型学会自主思考!开创性技术“自主认知”框架
ChatGPT、百度文心一言、Bard等大语言模型展现出了超强的创造能力,加速了生成式AI的应用进程。但AI模型只能基于训练数据执行各种任务,无法像人类一样利用生活知识、过往经验用于复杂的推理和决策。 例如,在玩游戏时,人类可以利用…...

Jmeter脚本参数化和正则匹配
我们在做接口测试过程中,往往会遇到以下几种情况 每次发送请求,都需要更改参数值为未使用的参数值,比如手机号注册、动态时间等 上一个接口的请求体参数用于下一个接口的请求体参数 上一个接口的响应体参数用于下一个接口的请求体参数&#…...

vue 请求代理 proxy
目录 为什么需要配置代理 什么是同源策略 如何配置代理 请求代理的原理 举例说明 为什么需要配置代理 因为浏览器的同源策略,当向和本地 devServer 服务器不同源的地址发送请求, 会违反浏览器的同源策略,导致发送失败,所以需…...

使用Spring Boot构建稳定可靠的分布式爬虫系统
摘要:本文将介绍如何使用Spring Boot框架构建稳定可靠的分布式爬虫系统。我们将从系统设计、任务调度、数据存储以及容灾与故障恢复等方面进行详细讲解,帮助读者理解并实践构建高效的分布式爬虫系统。 1. 引言 随着互联网的快速发展,爬虫系…...
分享一个查询OpenAI Chatgpt key余额查询的工具网站
OpenAI Key 余额查询工具 欢迎使用 OpenAI Key 余额查询工具网站!这个工具可以帮助您轻松地验证您的 OpenAI API 密钥,并查看您的余额。 http://tools.lbbit.top/check_key/ 什么是 OpenAI Key 余额查询工具? OpenAI Key 余额查询工具是一…...

【LeetCode刷题(数据结构与算法)】:二叉树的后序遍历
给你一棵二叉树的根节点root 返回其节点值的后序遍历 示例 1: 输入:root [1,null,2,3] 输出:[3,2,1] 示例 2: 输入:root [] 输出:[] 示例 3: 输入:root [1] 输出:[1]…...
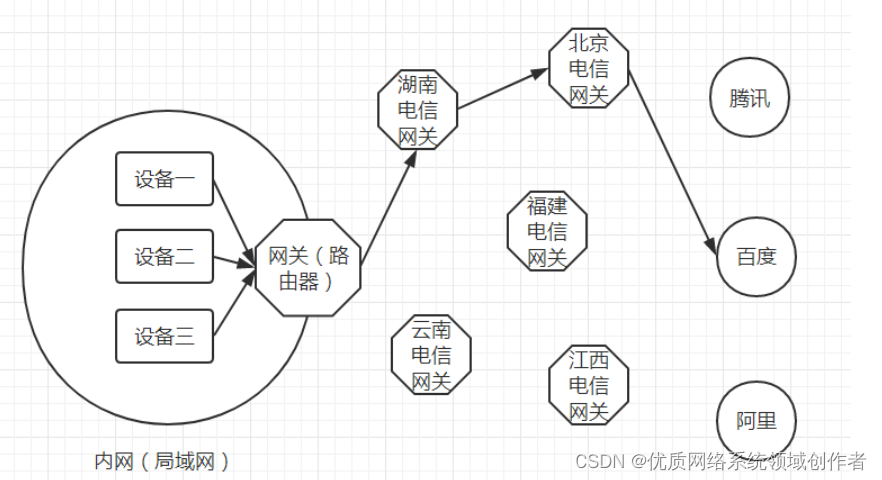
内网、外网、宽带、带宽、流量、网速之间的区别与联系
一.带宽与宽带的区别是什么? 带宽是量词,指的是网速的大小,比如1Mbps的意思是一兆比特每秒,这个数值就是指带宽。 宽带是名词,说明网络的传输速率速很高 。宽带的标准各不相同,最初认为128kbps以上带宽的就…...
打造类ChatGPT服务,本地部署大语言模型(LLM),如何远程访问?
ChatGPT的成功,让越来越多的人开始关注大语言模型(LLM)。如果拥有了属于自己的大语言模型,就可以对其进行一些专属优化。例如:打造属于自己的AI助理,或是满足企业自身的业务及信息安全需求。 所以ÿ…...

linux平台的无盘启动开发
by fanxiushu 2023-10-15 转载或引用请注明原始作者。 前一章节介绍的是linux平台下的虚拟磁盘驱动开发过程,主要讲述了 基于block的磁盘和基于SCSI接口的磁盘。 本文介绍的内容正是基于上文中的SCSI接口的虚拟磁盘实现的无盘启动。 同样的,linux系统下也…...
【GO入门】环境配置及Vscode配置
1 GO环境配置 欢迎来到Go的世界,让我们开始探索吧! Go是一种新的语言,一种并发的、带垃圾回收的、快速编译的语言。它具有以下特点: 它可以在一台计算机上用几秒钟的时间编译一个大型的Go程序。Go为软件构造提供了一种模型&…...
家政服务小程序,家政维修系统,专业家政软件开发商;家政服务小程序,家政行业软件开发
家政服务小程序,家政维修系统,专业家政软件开发商; 家政服务小程序,家政行业软件开发解决方案,家政软件经验丰富实践,系统高度集成,提供师傅端、用户端、… 家政服务app开发架构有 1、后台管理端…...

英语——语法——从句——状语从句——笔记
一、概念 状语从句(Adverbial Clause)是指句子用作状语时,起副词作用的句子。状语从句中的从句可以修饰谓语。 状语从句根据其作用可分为时间、地点、原因、条件、目的、结果、让步、方式和比较等九 种状语从句。状语从句一般由连词(从属连词…...

Linux 学习的六个过程
Linux 上手难,学习曲线陡峭,所以它的学习过程更像一个爬坡模式。这些坡看起来都很陡,但是一旦爬上一阶,就会一马平川。 1、抛弃旧的思维习惯,熟练使用 Linux 命令行 在 Linux 中,无论我们做什么事情&…...

『heqingchun-ubuntu系统下安装nvidia显卡驱动3种方法』
ubuntu系统下安装nvidia显卡驱动3种方法 一、安装依赖 1.更新 sudo apt updatesudo apt upgrade -y2.基础工具 sudo apt install -y build-essential python图形界面相关 sudo apt install -y lightdm注:在弹出对话框选择"lightdm" 二、第一种:使用…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...

Mysql中select查询语句的执行过程
目录 1、介绍 1.1、组件介绍 1.2、Sql执行顺序 2、执行流程 2.1. 连接与认证 2.2. 查询缓存 2.3. 语法解析(Parser) 2.4、执行sql 1. 预处理(Preprocessor) 2. 查询优化器(Optimizer) 3. 执行器…...
