金融数学方法:梯度下降法
1.算法介绍
梯度下降法是一种常用的优化算法,其通过沿着梯度下降的方向迭代寻找局部极小值。如果沿着梯度上升的方向迭代,就可以找到极大值。
在梯度下降法中,我们首先需要选择一个初始点 x 0 x_0 x0作为起始位置,然后计算当前位置的梯度(即函数在该点的导数)。接着,我们根据梯度的反方向来更新当前位置,使得函数值逐渐减小,直到达到局部最小值或收敛。梯度下降法的更新公式为 x n + 1 = x n − λ n ∇ F ( x n ) (1) x_{n+1}=x_n-\lambda_n \nabla F(x_n) \tag{1} xn+1=xn−λn∇F(xn)(1)其中, λ n \lambda_n λn是步长, ∇ F \nabla F ∇F是函数的梯度。
我们需要考虑一个问题,那就是步长 λ n \lambda_n λn应该如何选取。如果步长太短,可能要迭代很多次,如果步长太长,可能会走过,错过极值点。我们可以先选择一个任意长度的步长,然后尝试着走,如果函数值下降了,则进行下一步迭代,如果函数值没有下降,那么就可以将步长取为现有的这一步,再次尝试,直到函数值下降为止,至于初始步长的选取,可以按照Barzilai-Borwein方法来定义
λ n = ∣ ( x n − x n − 1 ) T ( ∇ F ( x n ) − ∇ F ( x n − 1 ) ) ∣ ∣ ∣ ∇ F ( x n ) − ∇ F ( x n − 1 ) ∣ ∣ 2 (2) \lambda_{n}=\frac{\left|\left(x_{n}-x_{n-1}\right)^{\mathrm{T}}\left(\nabla F\left(x_{n}\right)-\nabla F\left(x_{n-1}\right)\right)\right|}{|| \nabla F\left(x_{n}\right)-\nabla F\left(x_{n-1}\right)||^{2}} \tag{2} λn=∣∣∇F(xn)−∇F(xn−1)∣∣2 (xn−xn−1)T(∇F(xn)−∇F(xn−1)) (2)
2.算例分析
用梯度下降法求 F ( x , y ) = ( x − 1 ) 2 + ( y − 1 ) 2 F(x,y)=(x-1)^2+(y-1)^2 F(x,y)=(x−1)2+(y−1)2的极小值。
首先求出函数F的梯度 ∇ F ( x , y ) = ( 2 ( x − 1 ) , 2 ( y − 1 ) ) \nabla F(x,y)=(2(x-1),2(y-1)) ∇F(x,y)=(2(x−1),2(y−1)),然后利用上面介绍的算法过程进行实现,以下是python实现代码。
def hanshu(x,y):return (x-1)*(x-1)+(y-1)*(y-1)
def daoshu(x,y):return [2*(x-1),2*(y-1)]
def calculate_lamb(x0,y0,d0,x1,y1,d1):f1=(x1-x0)*(d1[0]-d0[0])+(y1-y0)*(d1[1]-d1[0])f2=(d1[0]-d0[0])**2+(d1[1]-d0[1])**2return f1/f2
def grad_descent(x0,y0):f0=hanshu(x0,y0)d0=daoshu(x0,y0)i,lamb=0,0.01while i<1000:x1,y1=x0-lamb*d0[0],y0-lamb*d0[1]f1=hanshu(x1,y1)while f1>f0:lamb=lamb*0.5x1,y1=x0-lamb*d0[0],y0-lamb*d0[1]f1=hanshu(x1,y1)if (x1-x0)**2+(y1-y0)**2<0.000001:breakd1=daoshu(x1,y1)lamb=calculate_lamb(x0,y0,d0,x1,y1,d1)x0,y0,f0,d0=x1,y1,f1,d1i+=1return x1,y1,i
这里取初始值(10,10),代入算法中求得最优解为(1.000538330078125, 1.000538330078125),这个值就已经很接近理论最小值(1,1)啦!
需要注意的是,梯度下降法可能会陷入局部最小值而无法找到全局最小值,因此在实践中常常会根据需求使用其他优化算法。同时,通过调节迭代次数等超参数,可以对梯度下降法进行优化,以获得更好的结果。
相关文章:

金融数学方法:梯度下降法
1.算法介绍 梯度下降法是一种常用的优化算法,其通过沿着梯度下降的方向迭代寻找局部极小值。如果沿着梯度上升的方向迭代,就可以找到极大值。 在梯度下降法中,我们首先需要选择一个初始点 x 0 x_0 x0作为起始位置,然后计算当前位…...

1031 查验身份证
一.问题: 一个合法的身份证号码由17位地区、日期编号和顺序编号加1位校验码组成。校验码的计算规则如下: 首先对前17位数字加权求和,权重分配为:{7,9,10,5,8,4…...

如何共享 Android 不同模块的构建配置
最近想重新梳理学习一遍 Android 的各个知识点,于是新建了一个 AndroidStudy 项目仓库,打算每个知识块新建 1 个 module。 类似这样: AndroidStudy (Root Project) ├─app (Module0) ├─CustomView (Module1) ├─KotlinCoroutines (Modul…...
atlas运维中遇到的问题
1、java.lang.NoClassDefFoundError:javax/ws/rs/core/Link$Builder 主要原因:jsr311-api包中javax.ws.rs.core包中没有Link类,而Atlas以HBase作为元数据存储,HBase本身使用的为javax.ws.rs-api包中的core包,其中有Lin…...
06-React的路由
06-React的路由 1.相关理解 1).SPA的理解 单页Web应用(single page web application,SPA)。整个应用只有一个完整的页面。点击页面中的链接不会刷新页面,只会做页面的局部更新。数据都需要通过ajax请求获取, 并在前端异步展现。…...
虹科方案 | 加州理工学院利用HK-TrueNAS开展地震研究
一、客户背景 加州理工学院(CalTech)是世界顶尖的理工类科学研究型学府之一。加州理工学院地震实验室是加州理工学院地质与行星科学部(GPS)的一个分支机构,成立于1921年,自20年代以来一直是世界地震学研究中心,并且几十年来一直是媒体对大地…...
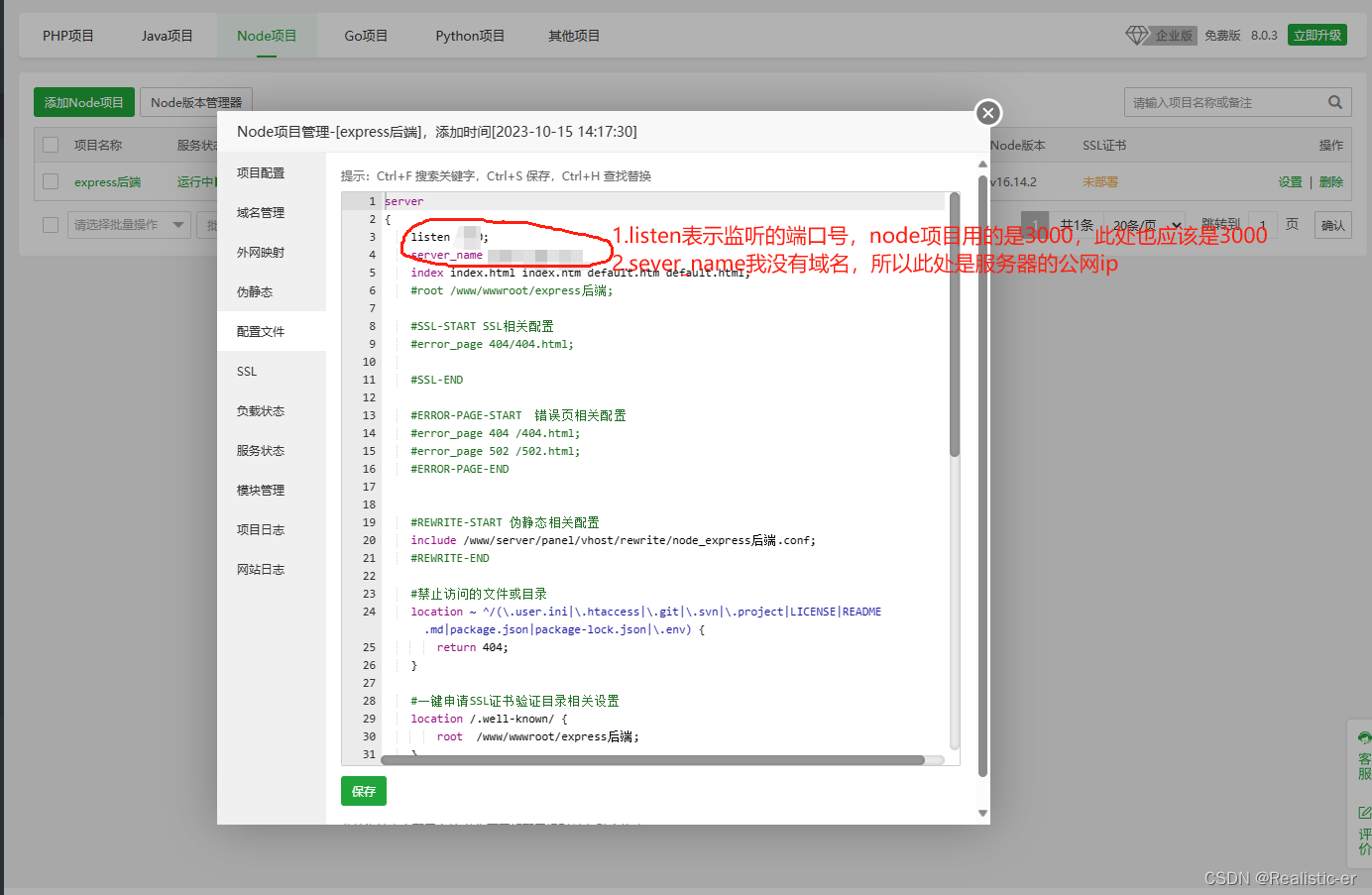
宝塔面板部署express以及MySql项目
第一次在宝塔面板上部署express和MySql项目,部署过程一直跑不通接口,特此记录一下。 在部署的时候,建议第一步把数据库MySql给跑通,中间好多原因是由于数据库的原因给引起的。 一.连接数据库 (1)在宝塔面…...
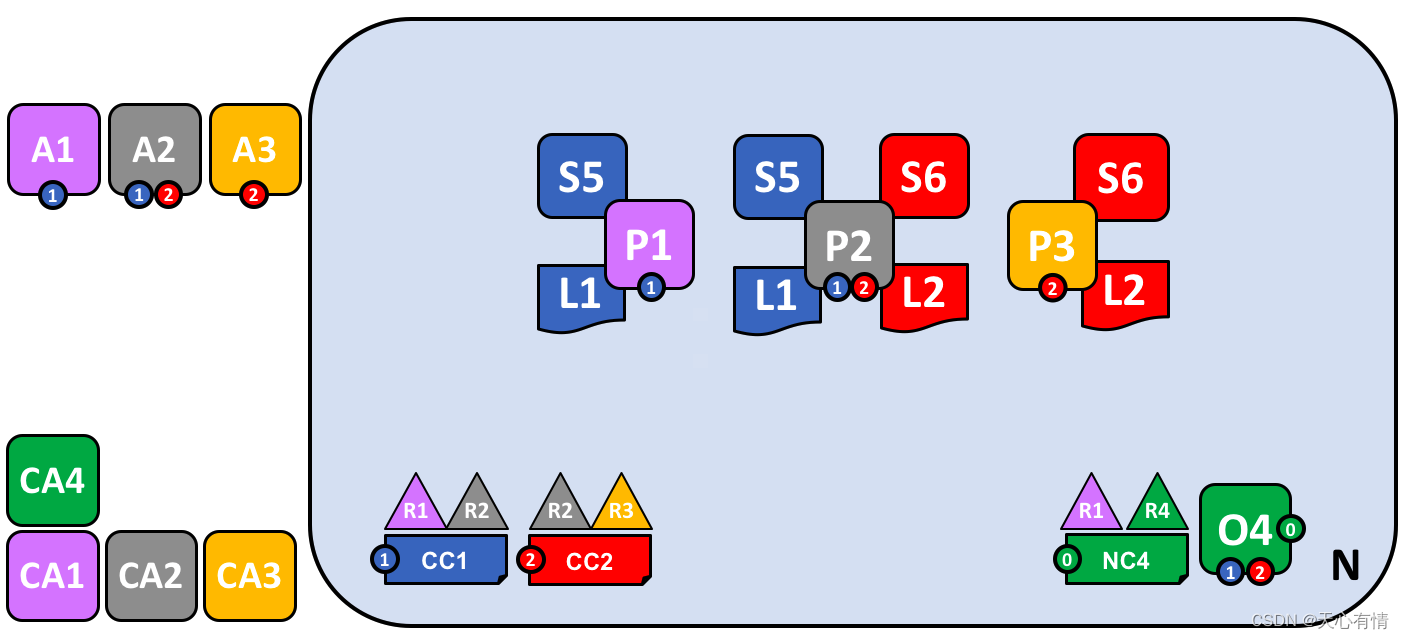
联盟链学习笔记-网络的创建
联盟链学习笔记 初始网络 下图是初始网络网络N的参考图 排序服务 在定义 网络 N 的时候,第一件事情就是定义一个 排序服务O4。O4 最初被配置并且由组织 R4 的一个管理员来启动,并且由 R4 管理。配置 NC4 包含了描述网络管理能力初始集合的规则。最初在…...

System.Drawing.Common.Bitmap跨平台的替代方案
使用SkiaSharp SkiaSharp是Skia Graphics Library的.Net跨平台实现,它可以在Windows,macOS,Linux,iOS,Android和其他平台上使用。 例如需要Linux版,则安装第一个和第四个: 以下是使用SkiaShar…...

深入理解 Java 泛型
没有泛型是怎样的 了解点 Java 历史的都知道,泛型是从 JDK 1.5 版本添加的特性,在 JDK1.5 之前,Java 很多特性都是没有的例如:泛型、注解、自动装箱和拆箱、可变参数。在介绍泛型之前,我们先来看看,如果没有泛型的世界是怎么样的。 假设有一个 List,我只想把 String 类…...
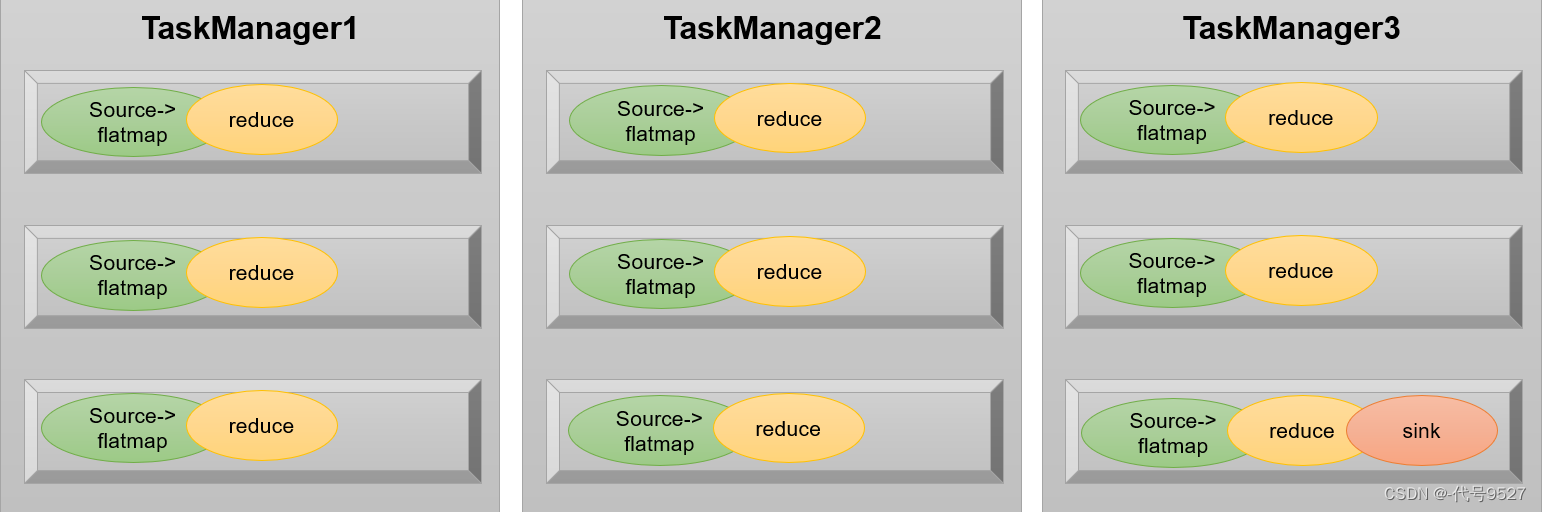
【基础篇】七、Flink核心概念
文章目录 1、并行度2、并行度的设置3、算子链4、禁用算子链5、任务槽6、任务槽和并行度的关系 1、并行度 要处理的数据量很多时,可以把一个算子的操作(比如前面demo里的flatMap、sum),"复制"多份到多个节点,…...

06-Scala面向对象
面向对象编程 Scala是一门完全面向对象的语言,摒弃了Java中很多不是面向对象的语法。 虽然如此,但其面向对象思想和 Java的面向对象思想还是一致的 Scala包 1)基本语法 Scala中基本的package包语法和 Java 完全一致 例如…...
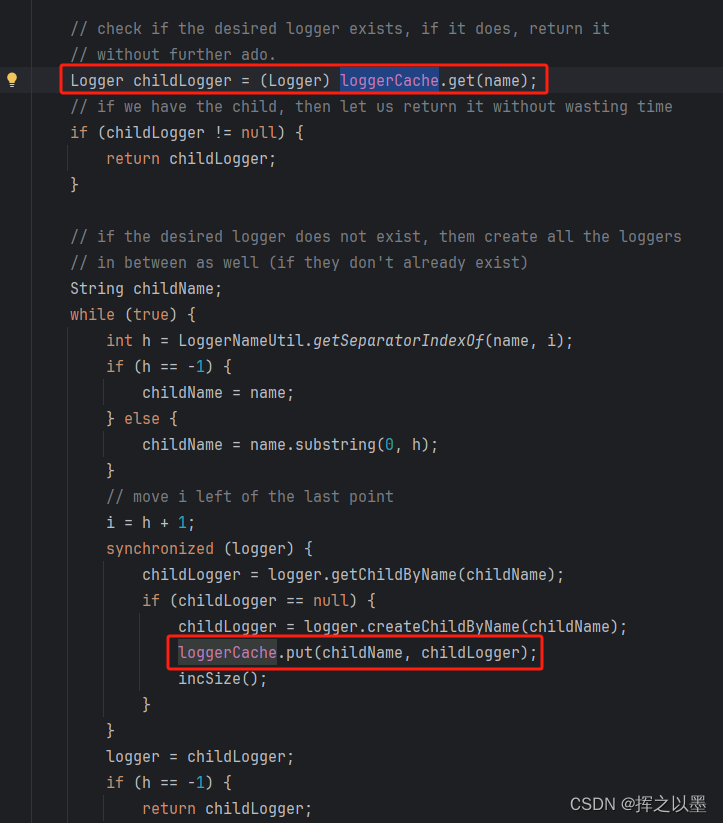
【设计模式】单例模式、“多例模式”的实现以及对单例的一些思考
文章目录 1.概述2.单例模式实现代码2.1.饿汉式单例2.2.懒汉式单例2.3.双检锁单例2.4.静态内部类单例2.5.枚举单例 3.对单例的一些思考3.1.是否需要严格的禁止单例被破坏?3.2.懒汉式真的比饿汉式更佳吗?3.3.单例存在的问题 4.其他作用范围的单例模式4.1.线…...
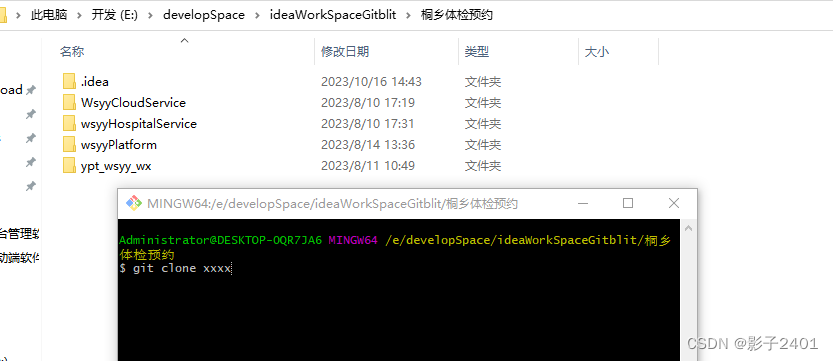
idea 2022 一个工作空间下导入git项目 后 无法导入第二个git项目
idea 2022 一个工作空间下导入git项目 后 无法导入第二个git项目 如图所示 我导入了一个git项目后,菜单栏出现了一个git按钮 找不到 导入git项目的按钮了 方式1、 通过idea设置 打开全局设置 如下图 把git先改为none,保存 保存后就可以看到 VCS按钮 导入…...

泛在电力物联网的关键技术与未来发展策略-安科瑞黄安南
摘要: 文章分析了泛在电力物联网的内涵及其主要特征,针对泛在电力物联网的建设目标、基本构架以及关键技术与未来发展策略进行综合探讨,期待得到专业人士的指点。 关键词: 泛在电力物联网, 网络规划, 网络发展 随着能源革命的不…...
iWall:支持自定义的Mac动态壁纸软件
iWall Mac是一款动态壁纸软件,它可以使用任何格式的漂亮视频(无须转换)、图片、动画、Flash、gif、swf、程序、网页、网站做为您的动态壁纸、动态桌面,并且可以进行交互。 这款软件功能多、使用简单、体积小巧、不占用资源、运行…...

【Docker 内核详解】namespace 资源隔离(四):Mount namespace Network namespace
【Docker 内核详解 - namespace 资源隔离】系列包含: namespace 资源隔离(一):进行 namespace API 操作的 4 种方式namespace 资源隔离(二):UTS namespace & IPC namespacenamespace 资源隔…...

STM32简介
STM32是ST公司基于ARM Cortex-M内核开发的32位微控制器,常应用在嵌入式领域如: 智能车(用stm32做寻迹小车,读取光电传感器或者摄像头数据,然后驱动电机前进和转弯); 无人机(用stm3…...

Yum安装JDK11
一、安装命令 : yum install java-11-openjdk二、执行以下命令来查看 JDK 11 的安装信息: yum list installed | grep java-11-openjdk三、找到 JDK 11 的软件包名称(使用以下命令来查询软件包的安装位置): rpm -ql…...
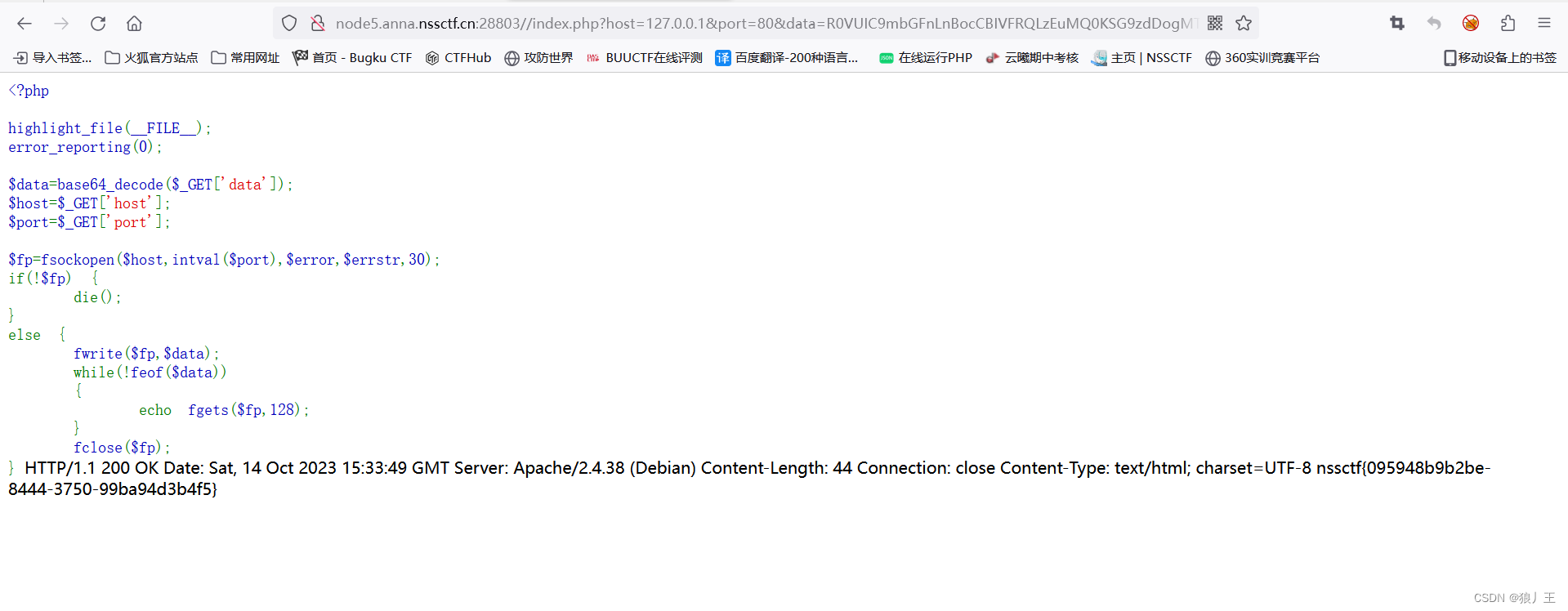
[HNCTF 2022 WEEK2]ez_ssrf题目解析
这题主要是引入ssrf这个漏洞攻击,本质上没有更深入的考察 本题是需要我们去伪造一个ssrf的请求头去绕过 题目开始给了我们信息让我们去访问index.php fsockopen函数触发ssrf fsockopen() 函数建立与指定主机和端口的 socket 连接。然后,它将传入的 bas…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...

LeetCode - 199. 二叉树的右视图
题目 199. 二叉树的右视图 - 力扣(LeetCode) 思路 右视图是指从树的右侧看,对于每一层,只能看到该层最右边的节点。实现思路是: 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...

LINUX 69 FTP 客服管理系统 man 5 /etc/vsftpd/vsftpd.conf
FTP 客服管理系统 实现kefu123登录,不允许匿名访问,kefu只能访问/data/kefu目录,不能查看其他目录 创建账号密码 useradd kefu echo 123|passwd -stdin kefu [rootcode caozx26420]# echo 123|passwd --stdin kefu 更改用户 kefu 的密码…...
