自动驾驶:控制算法概述
自动驾驶:控制算法概述
- 常见控制算法
- PID算法
- LQR算法
- MPC算法
- 自动驾驶控制算法
- 横向控制
- 纵向控制
- 参考文献
常见控制算法
PID算法
PID(Proportional-Integral-Derivative)控制是一种经典的反馈控制算法,通常用于稳定性和响应速度要求不是特别高的控制系统。PID控制基于三个主要组成部分:比例项(P),积分项(I),和微分项(D)。比例项根据当前误差来产生控制输出,积分项处理历史误差的总和,微分项处理误差变化的速度。PID控制通常通过多次试验、调整参数来实现,通过对PID参数的调节进而改善系统的性能,如稳定性、超调和振荡等。
PID控制算法的控制输出计算如下:
u ( t ) = K p ⋅ e ( t ) + K i ⋅ ∫ 0 t e ( τ ) d τ + K d ⋅ d e ( t ) d t u(t) = K_p\cdot e(t) + K_i \cdot \int_0^t e(\tau)d\tau + K_d \cdot \frac{de(t)}{dt} u(t)=Kp⋅e(t)+Ki⋅∫0te(τ)dτ+Kd⋅dtde(t)
其中, u ( t ) u(t) u(t)是控制输出, K p K_p Kp、 K i K_i Ki和 K d K_d Kd分别是比例、积分和微分系数, e ( t ) e(t) e(t)是当前误差, d e ( t ) d t \frac{de(t)}{dt} dtde(t)是误差的变化率。
- 比例项(P - Proportional):
比例项与当前误差成正比,用来调整控制输出。当前误差是期望值与实际值之间的差值。
比例项的作用是减小误差,使系统更快地接近期望值。
比例系数(通常表示为 K p K_p Kp)用来控制比例项的影响,过大的 K p K_p Kp可能引起超调,而过小的 K p K_p Kp可能导致响应过慢。 - 积分项(I - Integral):
积分项用来处理历史误差的总和。它消除系统的稳态误差,确保系统最终稳定在期望值附近。
积分项的作用是减小稳态误差,特别是在系统存在系统饱和或其他非线性问题时。
积分系数(通常表示为 K i K_i Ki)控制积分项的影响,过大的 K i K_i Ki可能导致系统不稳定,而过小的 K i K_i Ki可能使响应过慢。 - 微分项(D - Derivative):
微分项用来处理误差变化的速度,预测未来误差趋势。它有助于减小振荡和改善系统的响应速度。
微分项的作用是减小系统的振荡,尤其在系统响应速度需要控制的情况下。
微分系数(通常表示为 K d K_d Kd)控制微分项的影响,过大的 K d K_d Kd可能引起噪声敏感性,而过小的 K d K_d Kd可能无法改善振荡问题。
PID控制对于线性系统和某些非线性系统非常有效,但不适用于所有类型的系统,而且它需要多次试验不断调參才能满足系统性能要求。对于一些复杂系统,更高级控制策略可能更为合适。
LQR算法
LQR(Linear Quadratic Regulator)控制算法是一种用于线性系统的最优控制方法,旨在寻找一种最优的控制策略,以最小化一个线性二次性能指标。LQR控制输入是系统状态的线性组合以及反馈信号,输出控制信号。它可以用于稳态和动态控制以及应用于多变量系统,通过权重矩阵调整性能指标,以满足特定需求。LQR的设计需要系统的状态空间模型和性能指标,通常使用状态反馈来调整系统行为,并可以提供最优的控制输入,使系统稳定并满足性能要求。
- 系统模型
LQR控制的第一步是建立线性时间不变(LTI)系统的状态空间模型。这个模型通常由状态方程和输出方程组成。
状态方程描述了系统状态(状态向量)如何随时间演变,通常用如下形式表示:
x ˙ ( t ) = A x ( t ) + B u ( t ) \dot{x}(t) = Ax(t) + Bu(t) x˙(t)=Ax(t)+Bu(t)
输出方程描述了系统状态和控制输入之间的关系,通常用如下形式表示:
y ( t ) = C x ( t ) + D u ( t ) y(t) = Cx(t) + Du(t) y(t)=Cx(t)+Du(t)
其中, x ( t ) x(t) x(t)是状态向量, x ˙ ( t ) \dot{x}(t) x˙(t)是状态向量的导数, u ( t ) u(t) u(t)是控制输入, y ( t ) y(t) y(t)是系统的输出, A A A、 B B B、 C C C和 D D D是系统的矩阵参数。 - 性能指标
LQR控制的目标是最小化一个线性二次性能指标,通常称为LQR性能指标或成本函数。
LQR性能指标的一般形式如下:
J = ∫ 0 ∞ ( x T Q x + u T R u ) d t J = \int_0^\infty \left( x^T Q x + u^T R u \right) dt J=∫0∞(xTQx+uTRu)dt
其中, Q Q Q是状态权重矩阵, R R R是控制输入权重矩阵。这些权重矩阵可以用来调整性能指标的权重,以满足特定的性能要求。 - 最有控制策略
LQR控制通过求解Riccati方程来找到最优的控制策略。Riccati方程的一般形式如下:
A T P + P A − ( P B ) R − 1 ( B T P ) + Q = 0 A^T P + PA - (PB)R^{-1}(B^T P) + Q = 0 ATP+PA−(PB)R−1(BTP)+Q=0
这里, P P P是状态反馈矩阵,包含了最优控制策略的信息。 R R R和 Q Q Q是性能指标中的权重矩阵, A A A和 B B B是系统的状态方程参数。
一旦求解了Riccati方程,最优的状态反馈矩阵 P P P就可以用来计算最优的控制输入,通常如下:
u ( t ) = − R − 1 B T P x ( t ) u(t) = -R^{-1}B^T P x(t) u(t)=−R−1BTPx(t) - 闭环控制
一旦找到了最优的状态反馈矩阵PP,可以将其应用于系统,以实现闭环控制。
最优的控制输入可以通过 u ( t ) = − R − 1 B T P x ( t ) u(t) = -R^{-1}B^T P x(t) u(t)=−R−1BTPx(t)计算,并用于调整系统状态,使系统的性能指标最小化。
然而,LQR控制也有一些限制,主要是它要求系统是线性的,且系统参数必须是已知的。对于非线性系统或具有参数不确定性的系统,可能需要使用其他控制策略,如模型预测控制(MPC)。
MPC算法
MPC(Model Predictive Control)控制算法是一种先进的模型预测控制策略,通常用于复杂、非线性、时变和多变量系统。MPC的核心思想是在每个时刻基于系统数学模型对未来的系统行为进行预测,并通过优化来选择最优的控制输入序列,以满足性能和约束要求。MPC允许系统在考虑约束条件下实时调整控制策略,以满足性能和操作限制,它处理复杂系统和需要考虑多种约束的情况下非常有效。
- 系统模型:
MPC的核心是系统的动态模型,这个模型通常以状态空间形式表示,包括状态方程和输出方程。
状态方程描述了系统状态如何随时间演变,通常表示为:
x ( k + 1 ) = f ( x ( k ) , u ( k ) ) x(k+1) = f(x(k), u(k)) x(k+1)=f(x(k),u(k))
输出方程描述了系统状态和控制输入之间的关系,通常表示为:
y ( k ) = g ( x ( k ) ) y(k) = g(x(k)) y(k)=g(x(k))
在MPC中,系统模型通常是非线性的,但也可以是线性的。 - 性能指标:
MPC的目标是通过调整控制输入来最小化一个性能指标,通常是成本函数,以满足性能要求。
一般性能指标的形式如下:
J = ∑ k = 0 N − 1 ( ℓ ( x ( k ) , u ( k ) ) + m ( x ( N ) ) ) J = \sum_{k=0}^{N-1} \left( \ell(x(k), u(k)) + m(x(N)) \right) J=k=0∑N−1(ℓ(x(k),u(k))+m(x(N)))
其中, N N N是控制预测的时域长度, ℓ ( ⋅ ) \ell(\cdot) ℓ(⋅)表示每个时刻的瞬时成本, m ( ⋅ ) m(\cdot) m(⋅)表示终端成本。 - 控制预测:
在每个时刻,MPC对未来的系统行为进行预测,计算一系列控制输入,通常称为控制输入序列。
这些预测是通过模拟系统状态演变,基于当前状态和控制输入,利用系统模型来完成的。
预测时域通常涵盖多个时刻,以确保系统在未来时间内满足性能指标。 - 优化问题:
MPC使用一个优化算法来选择最优的控制输入序列,以最小化性能指标。
优化问题的目标是在满足约束条件的情况下,最小化性能指标。
优化问题通常是非线性的,并可以包括状态、控制输入和约束的非线性约束条件。 - 控制策略:
一旦找到最优的控制输入序列,只应用第一个控制输入,然后在下一个时刻重新计算。
这使得MPC成为一种适用于非线性系统和多变量系统的灵活控制策略,可以在实时中重新优化控制输入。 - 约束条件:
MPC可以处理各种约束条件,包括状态、控制输入和输出的约束。
这些约束可用于确保系统在操作限制内运行,以避免不稳定或不安全的操作。
然而,MPC控制算法需要较强的计算能力,因为它涉及到在线优化问题的求解。而且它对系统模型的准确性要求较高,可能需要对控制器的参数进行精细调整以实现所需的性能。
自动驾驶控制算法
自动驾驶控制往往是横纵向解耦控制,横向控制器一般采用LQR算法,而纵向控制器一般采用PID算法,下面将详细介绍横纵向控制。
横向控制
横向控制的输入车辆位置(定位信息)、车身参数信息(底盘信息)和规划轨迹,它主要通过改变方向盘扭矩或转角等进而控制车辆的前轮转角,使车辆按照规划的路径行驶。如下图所示,横向控制主要由前馈开环控制器和反馈闭环控制器构成。

纵向控制
纵向控制的输入为规划的位置、速度和加速度,它主要为速度控制,通过控制刹车和油门等实现对车速的控制,如下图所示,纵向控制主要由两个闭环控制和一个开环控制组成。

参考文献
Apollo代码学习(五)—横纵向控制
相关文章:

自动驾驶:控制算法概述
自动驾驶:控制算法概述 常见控制算法PID算法LQR算法MPC算法 自动驾驶控制算法横向控制纵向控制 参考文献 常见控制算法 PID算法 PID(Proportional-Integral-Derivative)控制是一种经典的反馈控制算法,通常用于稳定性和响应速度要…...
【Mysql】Mysql的字符集和比较规则(三)
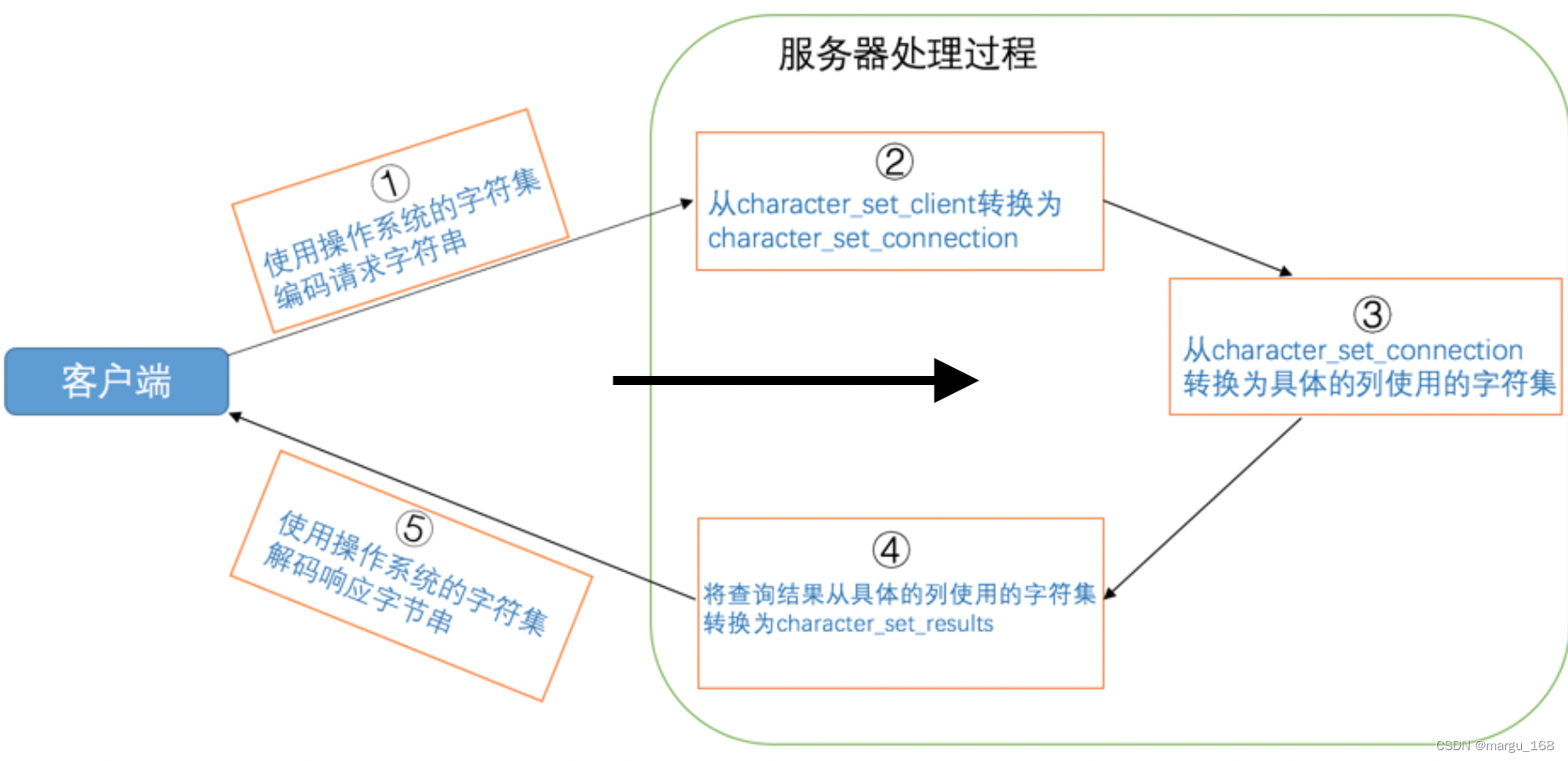
字符集和比较规则简介 字符集简介 我们知道在计算机中只能以二进制的方式对数据进行存储,那么他们之间是怎样对应并进行转换的?我们需要了解两个概念: 字符范围:我们可以将哪些字符转换成二进制数据,也就是规定好字…...
【SpringCloud-11】SCA-sentinel
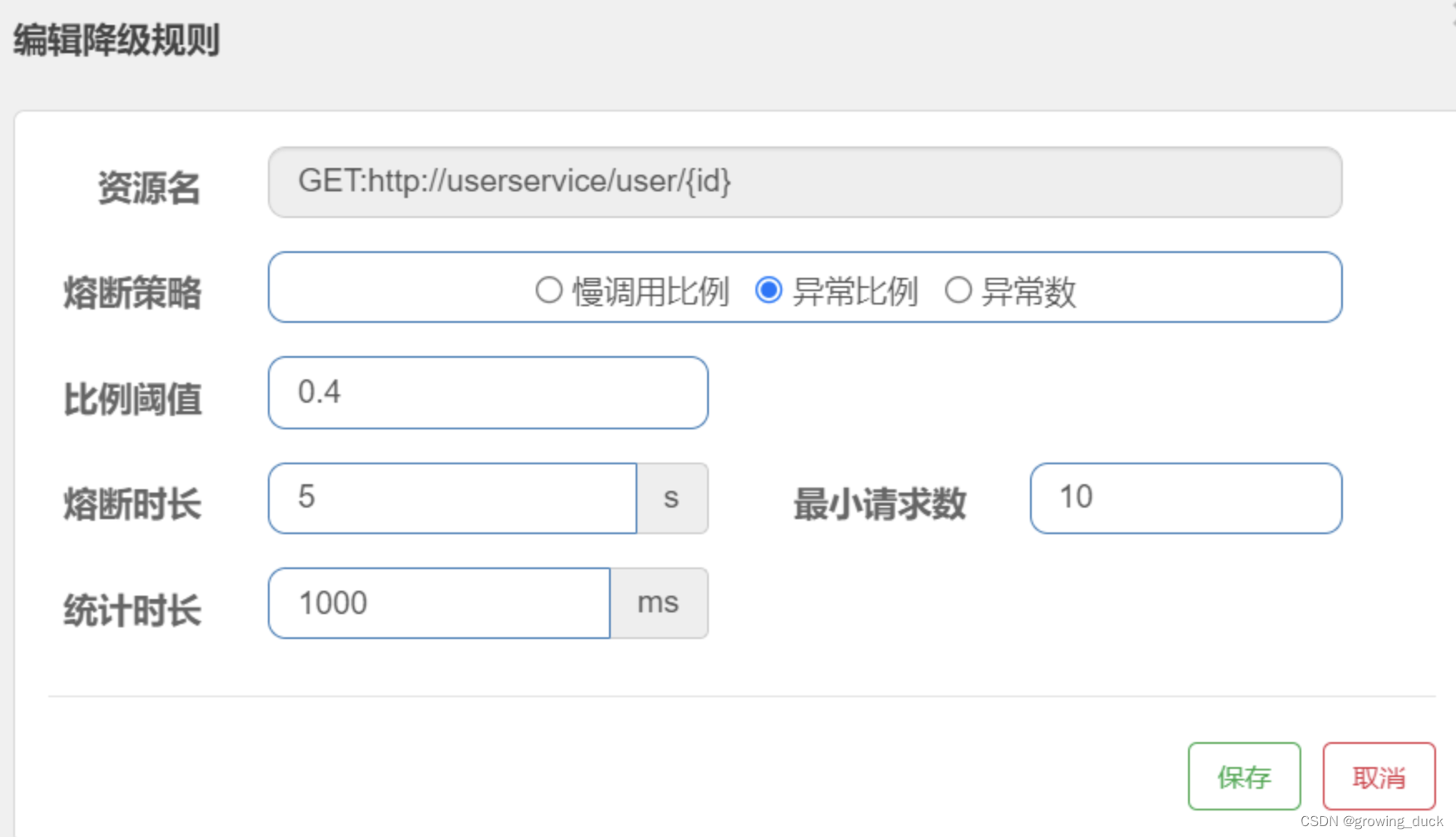
sentinel是一个流量控制、熔断降级的组件,可以替换第一代中的hystrix。 hystrix用起来没有那么方便: 1、要在调用方引入hystrix,没有ui界面进行配置,需要在代码中进行配置,侵入了业务代码。 2、还要自己搭建监控平台…...
设计模式:简单工厂模式(C#、JAVA、JavaScript、C++、Python、Go、PHP):
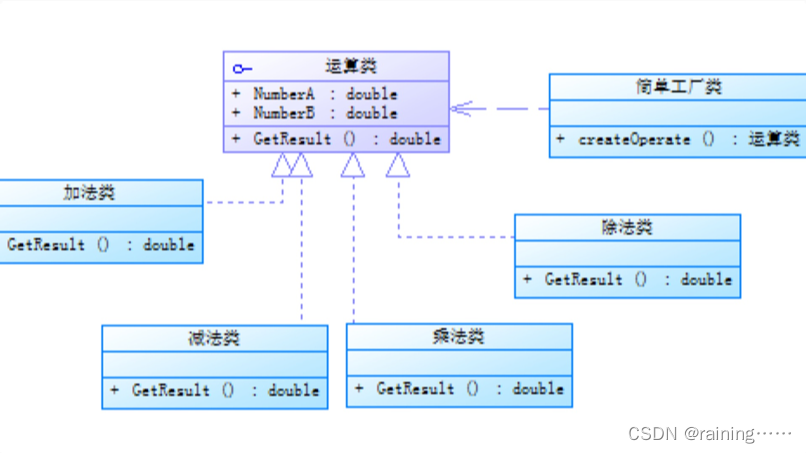
简介: 简单工厂模式,它提供了一个用于创建对象的接口,但具体创建的对象类型可以在运行时决定。这种模式通常用于创建具有共同接口的对象,并且可以根据客户端代码中的参数或配置来选择要创建的具体对象类型。 在简单工厂模式中&am…...
浅谈智能照明控制系统在智慧建筑中的应用
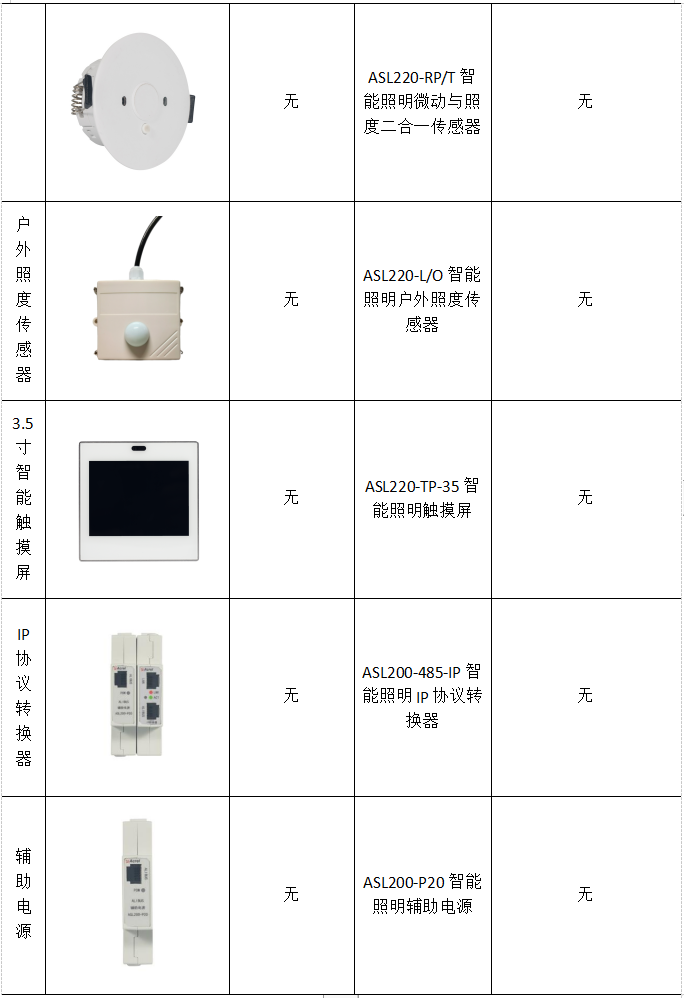
贾丽丽 安科瑞电气股份有限公司 上海嘉定 201801 摘要:新时期,建筑行业发展迅速,在信息化背景下,建筑功能逐渐拓展,呈现了智能化的发展态势。智能建筑更加安全、节能、环保,也符合绿色建筑理念。在建筑智…...
以及upper_bound())
lower_bound()以及upper_bound()
lower_bound(): lower_bound()的返回值是第一个大于等于 target 的值的地址,用这个地址减去first,得到的就是第一个大于等于target的值的下标。 在数组中: int poslower_bound(a,an,target)-a;\\n为数组…...
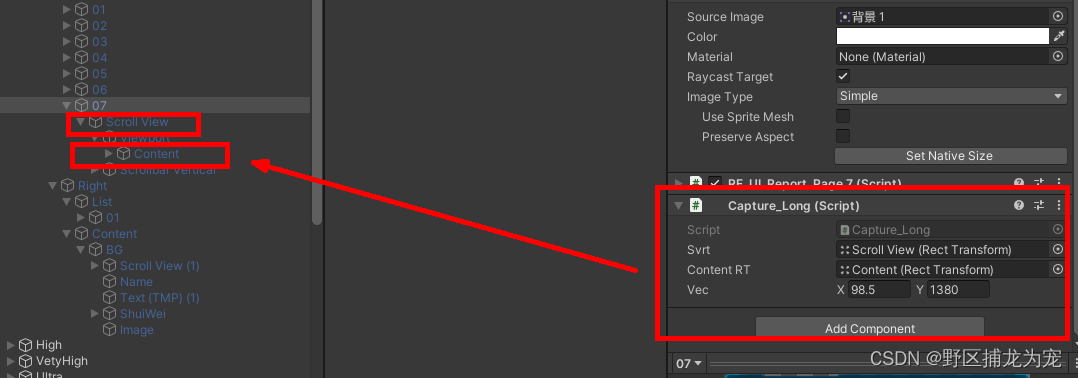
unity(WebGL) 截图拼接并保存本地,下载PDF
截图参考:Unity3D 局部截图、全屏截图、带UI截图三种方法_unity 截图_野区捕龙为宠的博客-CSDN博客 文档下载: Unity WebGL 生成doc保存到本地电脑_unity webgl 保存文件_野区捕龙为宠的博客-CSDN博客 中文输入:Unity WebGL中文输入 支持输…...

加速企业云计算部署:应对新时代的挑战
随着科技的飞速发展,企业面临着诸多挑战。在这个高度互联的世界中,企业的成功与否常常取决于其能否快速、有效地响应市场的变化。云计算作为一种新兴的技术趋势,为企业提供了实现这一目标的可能。通过加速企业云计算部署,企业可以…...

ubuntu 18.04 LTS交叉编译opencv 3.4.16并编译工程[全记录]
一、下载并解压opencv 3.4.16源码 https://opencv.org/releases/ 放到home路径下的Exe文件夹(专门放用户安装的软件)中,其中build是后期自建的 为了版本控制,保留了3.4.16,并增加了-gcc-arm 二、安装cmake和cmake-g…...
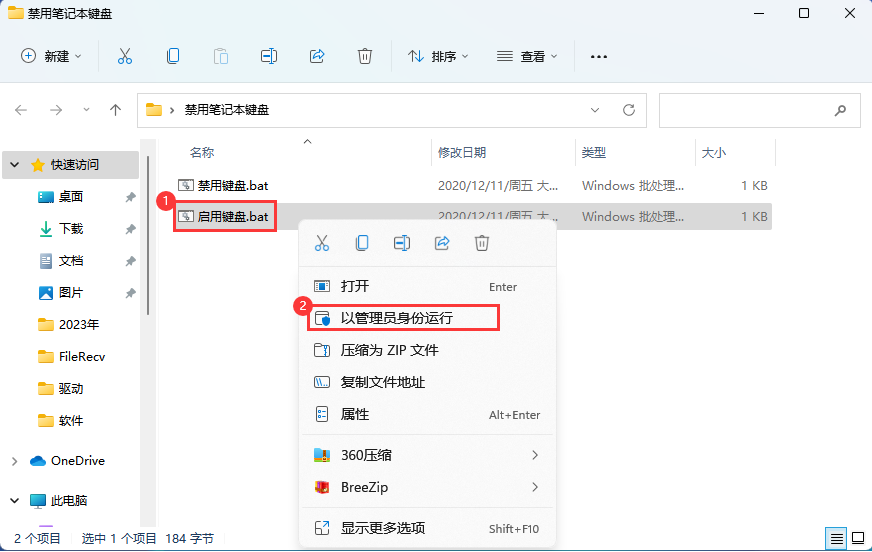
禁用和开启笔记本电脑的键盘功能,最快的方式
笔记本键盘通常较小,按键很不方便,当我们外接了键盘时就不需要再使用自带的键盘了,而且午睡的时候,总是担心碰到笔记本的键盘,可能会删掉我们的代码什么的,所以就想着怎么禁用掉,下面是操作步骤…...
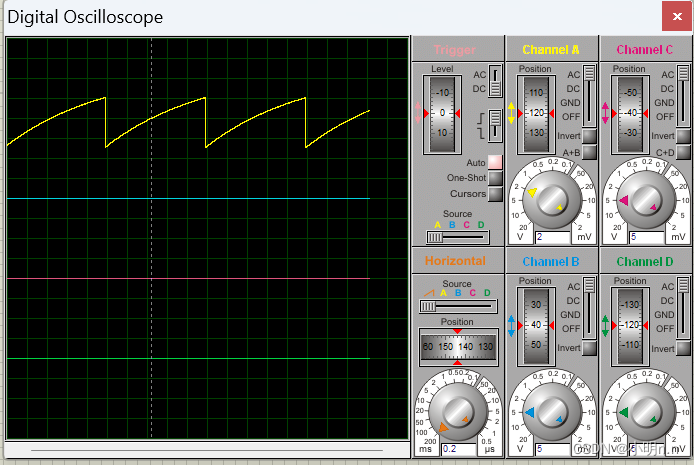
【单片机基础】使用51单片机制作函数信号发生器(DAC0832使用仿真)
文章目录 (1)DA转换(2)DAC0832简介(3)电路设计(4)参考例程(5)参考文献 (1)DA转换 单片机作为一个数字电路系统,当需要采集…...
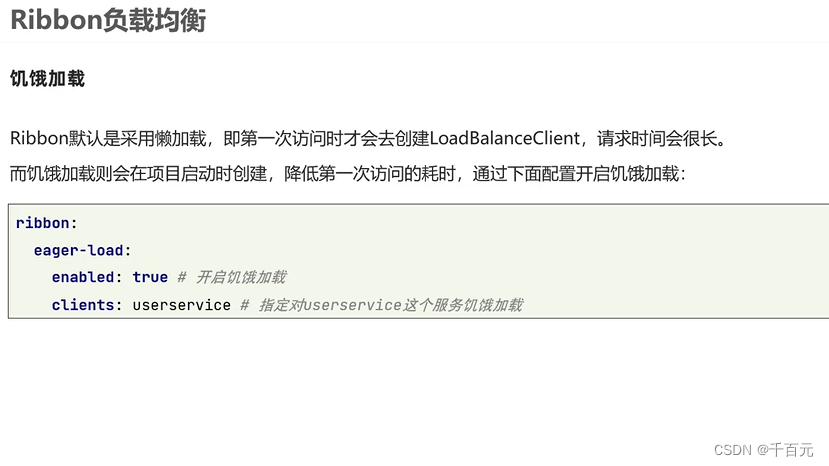
springcloud组件
https://www.bilibili.com/video/BV1QX4y1t7v5?p32&vd_source297c866c71fa77b161812ad631ea2c25 eureka : 主要是收集服务的注册信息。 如果有了eureka启动了。内部之前的调用其实就可以用服务名了, 本来是要是用ip端口来访问的,只要eureka启来了…...

手机爬虫用Appium详细教程:利用Python控制移动App进行自动化抓取数据
Appium是一个强大的跨平台工具,它可以让你使用Python来控制移动App进行自动化操作,从而实现数据的抓取和处理。今天,我将与大家分享一份关于使用Appium进行手机爬虫的详细教程,让我们一起来探索Appium的功能和操作,为手…...

deb包构建详解
deb包构建详解 一、deb包构建流程二、deb包构建描述文件详解2.1 control文件2.2 postinst 文件 (post-installation script)2.3 postrm 文件 (post-removal script)2.4 prerm 文件 (pre-removal script)2.5 preinst 文件 (pre-installation script)2.6 rules 文件2.7 changelog…...

【Spring Cloud】网关Gateway的请求过滤工厂RequestRateLimiterGatewayFilterFactory
概念 关于微服务网关Gateway中有几十种过滤工厂,这一篇博文记录的是关于请求限流过滤工厂,也就是标题中的RequestRateLimiterGatewayFilterFactory。这个路由过滤工厂是用来判断当前请求是否应该被处理,如果不会被处理就会返回HTTP状态码为42…...

自己写spring boot starter问题总结
1. Unable to find main class 创建spring boot项目写自己的starterxi写完之后使用install出现Unable to find main class,这是因为spring boot打包需要一个启动类,按照以下写法就没事 <plugins><plugin><groupId>org.springframewo…...

vue3如何打开页面即向后端发送请求
目录 背景: 实现: 1、使用 2、案例 补充: 1、如何定义一个集合来接受后端返回的list 2、加入请求头 背景: 如果想在页面刚加载时向后端发送请求,可以使用Vue 3的生命周期钩子函数onMounted来实现 实现ÿ…...

【软考】9.2 串/数组/矩阵/广义表/树
《字符串》 一种特殊的线性表,数据元素都为字符模式匹配:寻找子串第一次在主串出现的位置 模式匹配算法 1. 暴力破解法(布鲁特-福斯算法) 主串与子串一个个匹配效率低 2. KMP算法 主串后缀和子串前缀能否找到一样的元素…...
大数据 DataX 数据同步数据分析入门
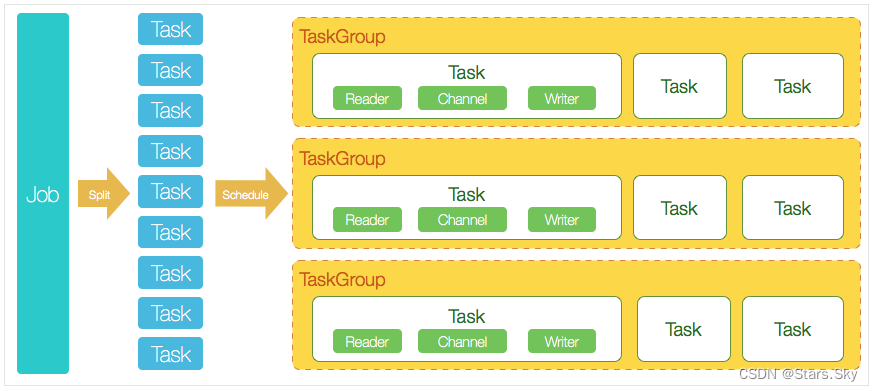
目录 一、DataX 概览 1.1 DataX 是什么 1.2 DataX 3.0 概览 设计理念 当前使用现状 二、DataX 详解 2.1 DataX 3.0 框架设计 2.2 DataX 3.0 插件体系 2.3 DataX 3.0 核心架构 2.3.1 核心模块介绍 2.3.2 DataX 调度流程 2.4 DataX 3.0 的六大核心优势 2.4.1 可靠的…...

【京东开源项目】微前端框架MicroApp 1.0正式发布
介绍 MicroApp是由京东前端团队推出的一款微前端框架,它从组件化的思维,基于类WebComponent进行微前端的渲染,旨在降低上手难度、提升工作效率。MicroApp无关技术栈,也不和业务绑定,可以用于任何前端框架。 源码地址…...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...

C++ 基础特性深度解析
目录 引言 一、命名空间(namespace) C 中的命名空间 与 C 语言的对比 二、缺省参数 C 中的缺省参数 与 C 语言的对比 三、引用(reference) C 中的引用 与 C 语言的对比 四、inline(内联函数…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...

ABAP设计模式之---“简单设计原则(Simple Design)”
“Simple Design”(简单设计)是软件开发中的一个重要理念,倡导以最简单的方式实现软件功能,以确保代码清晰易懂、易维护,并在项目需求变化时能够快速适应。 其核心目标是避免复杂和过度设计,遵循“让事情保…...

使用Spring AI和MCP协议构建图片搜索服务
目录 使用Spring AI和MCP协议构建图片搜索服务 引言 技术栈概览 项目架构设计 架构图 服务端开发 1. 创建Spring Boot项目 2. 实现图片搜索工具 3. 配置传输模式 Stdio模式(本地调用) SSE模式(远程调用) 4. 注册工具提…...

站群服务器的应用场景都有哪些?
站群服务器主要是为了多个网站的托管和管理所设计的,可以通过集中管理和高效资源的分配,来支持多个独立的网站同时运行,让每一个网站都可以分配到独立的IP地址,避免出现IP关联的风险,用户还可以通过控制面板进行管理功…...

职坐标物联网全栈开发全流程解析
物联网全栈开发涵盖从物理设备到上层应用的完整技术链路,其核心流程可归纳为四大模块:感知层数据采集、网络层协议交互、平台层资源管理及应用层功能实现。每个模块的技术选型与实现方式直接影响系统性能与扩展性,例如传感器选型需平衡精度与…...

MLP实战二:MLP 实现图像数字多分类
任务 实战(二):MLP 实现图像多分类 基于 mnist 数据集,建立 mlp 模型,实现 0-9 数字的十分类 task: 1、实现 mnist 数据载入,可视化图形数字; 2、完成数据预处理:图像数据维度转换与…...
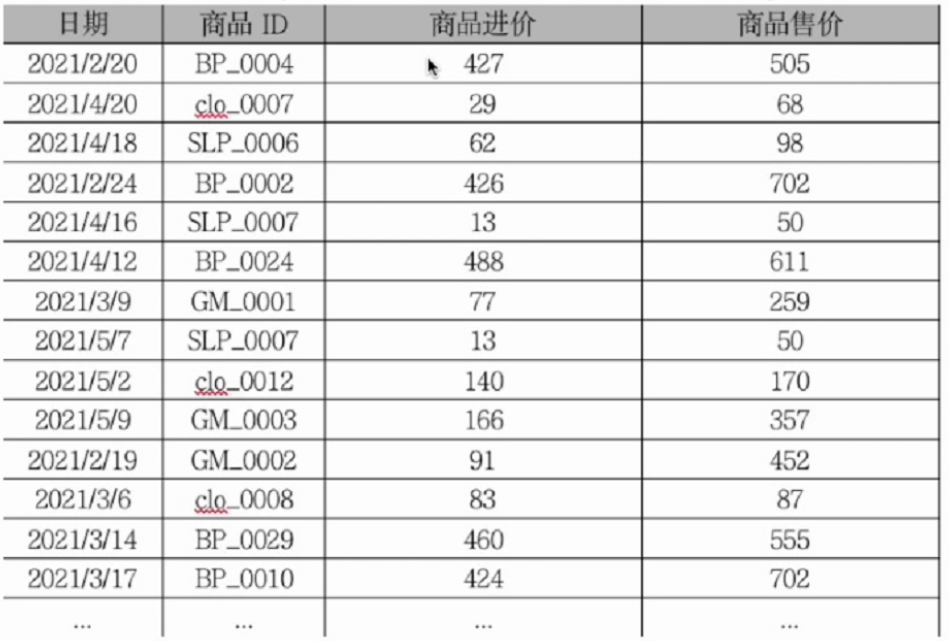
智警杯备赛--excel模块
数据透视与图表制作 创建步骤 创建 1.在Excel的插入或者数据标签页下找到数据透视表的按钮 2.将数据放进“请选择单元格区域“中,点击确定 这是最终结果,但是由于环境启不了,这里用的是自己的excel,真实的环境中的excel根据实训…...
