C#,数值计算——分类与推理Gaumixmod的计算方法与源程序

1 文本格式
using System;
using System.Collections.Generic;
namespace Legalsoft.Truffer
{
public class Gaumixmod
{
private int nn { get; set; }
private int kk { get; set; }
private int mm { get; set; }
private double[,] data { get; set; }
private double[,] means { get; set; }
private double[,] resp { get; set; }
private double[] frac { get; set; }
private double[] lndets { get; set; }
private double[,,] sig { get; set; }
private double loglike { get; set; }
public Gaumixmod(double[,] ddata, double[,] mmeans)
{
int mmstat = ddata.GetLength(1);
this.nn = ddata.GetLength(0);
this.kk = mmeans.GetLength(0);
this.mm = mmstat;
this.data = Globals.CopyFrom(ddata);
this.means = Globals.CopyFrom(mmeans);
this.resp = new double[nn, kk];
this.frac = new double[kk];
this.lndets = new double[kk];
this.sig = new double[kk, mmstat, mmstat];
for (int k = 0; k < kk; k++)
{
frac[k] = 1.0 / kk;
for (int i = 0; i < mm; i++)
{
for (int j = 0; j < mm; j++)
{
sig[k, i, j] = 0.0;
}
sig[k, i, i] = 1.0e-10;
}
}
estep();
mstep();
}
public double estep()
{
double[] u = new double[mm];
double[] v = new double[mm];
double oldloglike = loglike;
for (int k = 0; k < kk; k++)
{
//Cholesky choltmp = new Cholesky(sig[k]);
Cholesky choltmp = new Cholesky(Globals.CopyFrom(k, sig));
lndets[k] = choltmp.logdet();
for (int n = 0; n < nn; n++)
{
for (int m = 0; m < mm; m++)
{
u[m] = data[n, m] - means[k, m];
}
choltmp.elsolve(u, v);
double sum = 0.0;
for (int m = 0; m < mm; m++)
{
sum += Globals.SQR(v[m]);
}
resp[n, k] = -0.5 * (sum + lndets[k]) + Math.Log(frac[k]);
}
}
loglike = 0;
for (int n = 0; n < nn; n++)
{
double max = -99.9e99;
for (int k = 0; k < kk; k++)
{
if (resp[n, k] > max)
{
max = resp[n, k];
}
}
double sum = 0.0;
for (int k = 0; k < kk; k++)
{
sum += Math.Exp(resp[n, k] - max);
}
double tmp = max + Math.Log(sum);
for (int k = 0; k < kk; k++)
{
resp[n, k] = Math.Exp(resp[n, k] - tmp);
}
loglike += tmp;
}
return loglike - oldloglike;
}
public void mstep()
{
for (int k = 0; k < kk; k++)
{
double wgt = 0.0;
for (int n = 0; n < nn; n++)
{
wgt += resp[n, k];
}
frac[k] = wgt / nn;
for (int m = 0; m < mm; m++)
{
double sum = 0.0;
for (int n = 0; n < nn; n++)
{
sum += resp[n, k] * data[n, m];
}
means[k, m] = sum / wgt;
for (int j = 0; j < mm; j++)
{
sum = 0.0;
for (int n = 0; n < nn; n++)
{
sum += resp[n, k] * (data[n, m] - means[k, m]) * (data[n, j] - means[k, j]);
}
sig[k, m, j] = sum / wgt;
}
}
}
}
}
}
2 代码格式
using System;
using System.Collections.Generic;namespace Legalsoft.Truffer
{public class Gaumixmod{private int nn { get; set; }private int kk { get; set; }private int mm { get; set; }private double[,] data { get; set; }private double[,] means { get; set; }private double[,] resp { get; set; }private double[] frac { get; set; }private double[] lndets { get; set; }private double[,,] sig { get; set; }private double loglike { get; set; }public Gaumixmod(double[,] ddata, double[,] mmeans){int mmstat = ddata.GetLength(1);this.nn = ddata.GetLength(0);this.kk = mmeans.GetLength(0);this.mm = mmstat;this.data = Globals.CopyFrom(ddata);this.means = Globals.CopyFrom(mmeans);this.resp = new double[nn, kk];this.frac = new double[kk];this.lndets = new double[kk];this.sig = new double[kk, mmstat, mmstat];for (int k = 0; k < kk; k++){frac[k] = 1.0 / kk;for (int i = 0; i < mm; i++){for (int j = 0; j < mm; j++){sig[k, i, j] = 0.0;}sig[k, i, i] = 1.0e-10;}}estep();mstep();}public double estep(){double[] u = new double[mm];double[] v = new double[mm];double oldloglike = loglike;for (int k = 0; k < kk; k++){//Cholesky choltmp = new Cholesky(sig[k]);Cholesky choltmp = new Cholesky(Globals.CopyFrom(k, sig));lndets[k] = choltmp.logdet();for (int n = 0; n < nn; n++){for (int m = 0; m < mm; m++){u[m] = data[n, m] - means[k, m];}choltmp.elsolve(u, v);double sum = 0.0;for (int m = 0; m < mm; m++){sum += Globals.SQR(v[m]);}resp[n, k] = -0.5 * (sum + lndets[k]) + Math.Log(frac[k]);}}loglike = 0;for (int n = 0; n < nn; n++){double max = -99.9e99;for (int k = 0; k < kk; k++){if (resp[n, k] > max){max = resp[n, k];}}double sum = 0.0;for (int k = 0; k < kk; k++){sum += Math.Exp(resp[n, k] - max);}double tmp = max + Math.Log(sum);for (int k = 0; k < kk; k++){resp[n, k] = Math.Exp(resp[n, k] - tmp);}loglike += tmp;}return loglike - oldloglike;}public void mstep(){for (int k = 0; k < kk; k++){double wgt = 0.0;for (int n = 0; n < nn; n++){wgt += resp[n, k];}frac[k] = wgt / nn;for (int m = 0; m < mm; m++){double sum = 0.0;for (int n = 0; n < nn; n++){sum += resp[n, k] * data[n, m];}means[k, m] = sum / wgt;for (int j = 0; j < mm; j++){sum = 0.0;for (int n = 0; n < nn; n++){sum += resp[n, k] * (data[n, m] - means[k, m]) * (data[n, j] - means[k, j]);}sig[k, m, j] = sum / wgt;}}}}}
}
相关文章:

C#,数值计算——分类与推理Gaumixmod的计算方法与源程序
1 文本格式 using System; using System.Collections.Generic; namespace Legalsoft.Truffer { public class Gaumixmod { private int nn { get; set; } private int kk { get; set; } private int mm { get; set; } private double…...

【Android】Intel HAXM installation failed!
Android Studio虚拟机配置出现Intel HAXM installation failed 如果方案一解决没有作用,就用方案二再试一遍 解决方案一: 1.打开控制面板 2.点击左侧下面最后一个程序 3.点击启用或关闭Windows功能 4.勾选Windows虚拟机监控程序平台 5.接下来重启电脑…...

2023年中国自动驾驶卡车市场发展趋势分析:自动驾驶渗透率快速增长[图]
自动驾驶卡车的技术原理是通过电脑算法控制车辆行驶,辅助驾驶员完成任务。其实现方式主要是基于传感器和计算处理技术。自动驾驶卡车可以随时感知周围环境,灵活避障,自适应调整行驶路径,相比之下传统卡车需要驾驶员进行手动操作&a…...

力扣第17题 电话号码的字母组合 c++ 回溯 经典提升题
题目 17. 电话号码的字母组合 中等 相关标签 哈希表 字符串 回溯 给定一个仅包含数字 2-9 的字符串,返回所有它能表示的字母组合。答案可以按 任意顺序 返回。 给出数字到字母的映射如下(与电话按键相同)。注意 1 不对应任何字母。…...

华纳云:怎么判断VPS的ip是不是公网ip
要判断一个VPS的IP地址是否为公网IP,您可以执行以下步骤: 查看IP地址: 首先,获取您的VPS的IP地址。您可以使用以下命令来查看VPS的IP地址: curl ifconfig.me 或 curl ipinfo.io/ip 这些命令将显示VPS的公网IP地址。 检…...

QT学习笔记1-Hello, QT
1. QT环境 1.1 QT_CREATOR QT的集成开发工具,可以进行项目的创建运行。有一些实例可以运行之。 1.2 QT_ASSISTANT QT的工具书 2. 核心的概念 2.1 windows 窗口 2.2 widget 组件放置在窗口上的 2.3 bar 栏 2.4 icon 图标 3. Hello, QT 3.1 main.cpp …...

水滴卡片效果实现
效果展示 CSS 知识点 border-radius 属性运用 FANCY-BORDER-RADIUS 工具 此工具主要是实现不规则的图形。 FANCY-BORDER-RADIUS 工具地址 页面整体布局实现 <div class"container"><div class"drop" style"--clr: #ff0f5b">&l…...

【算法题】2899. 上一个遍历的整数
插: 前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不住分享一下给大家。点击跳转到网站。 坚持不懈,越努力越幸运,大家一起学习鸭~~~ 题目: 给你一个下标从 0 开始的字符串数组…...

Python+unittest+requests接口自动化测试框架搭建 完整的框架搭建过程
首先配置好开发环境,下载安装Python并下载安装pycharm,在pycharm中创建项目功能目录。如果不会的可以百度Google一下,该内容网上的讲解还是比较多比较全的! 大家可以先简单了解下该项目的目录结构介绍,后面会针对每个文…...

系统架构设计:19 论数据挖掘技术的应用
目录 一 数据挖掘技术 1 数据挖掘的分类 2 数据挖掘的主要方法 一 数据挖掘技术 从技术角度看,数据挖掘可以定义为从大量的、不完全的、有噪声的、模糊的、随机的实际数据中提取隐含在其中的、人们不知道的、但又潜在有用的信息和知识的过程。</...

如何选择高防CDN和高防IP?
目录 前言 一、对高防CDN的选择 1. 加速性能 2. 抗攻击能力 3. 全球覆盖能力 4. 可靠性和稳定性 二、对高防IP的选择 1. 防御能力 2. 服务质量 3. 安全性 4. 价格 三、高防CDN和高防IP的优缺点对比 1. 高防CDN的优缺点 2. 高防IP的优缺点 总结 前言 随着互联网…...
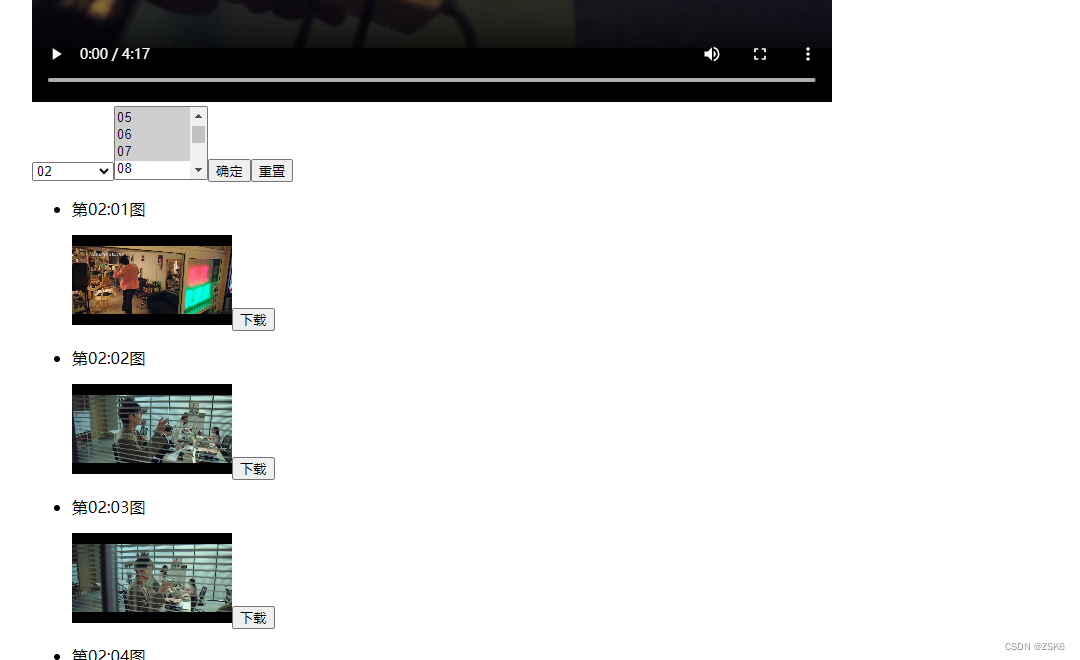
【html】利用生成器函数和video元素,取出指定时间的视频画面
简言 有的时候想截取视频某一秒的视频画面。 手动截取操作麻烦,还得时刻关注视频播放时间。 于是,我搞出来了一个根据视频自动截取特定时间描述的页面。 效果 实现步骤 获取视频对象根据视频时长生成时间选择表单根据表单选择的时间和视频地址&#x…...

第五十九章 学习常用技能 - 将数据从一个数据库移动到另一个数据库
文章目录 第五十九章 学习常用技能 - 将数据从一个数据库移动到另一个数据库 第五十九章 学习常用技能 - 将数据从一个数据库移动到另一个数据库 如果需要将数据从一个数据库移动到另一个数据库,请执行以下操作: 识别包含数据及其索引的Global。 如果…...
虚拟示波器的设计与实现
摘 要 针对传统示波器功能单一、不方便更新升级的缺陷,本文基于虚拟仪器软件LabVIEW和NI PCI-6221数据采集卡设计并实现了一种多功能虚拟示波器,该虚拟示波器不仅具有采集和显示实际信号时域波形的功能,还具有信号产生、波形存储等功能。 测试…...
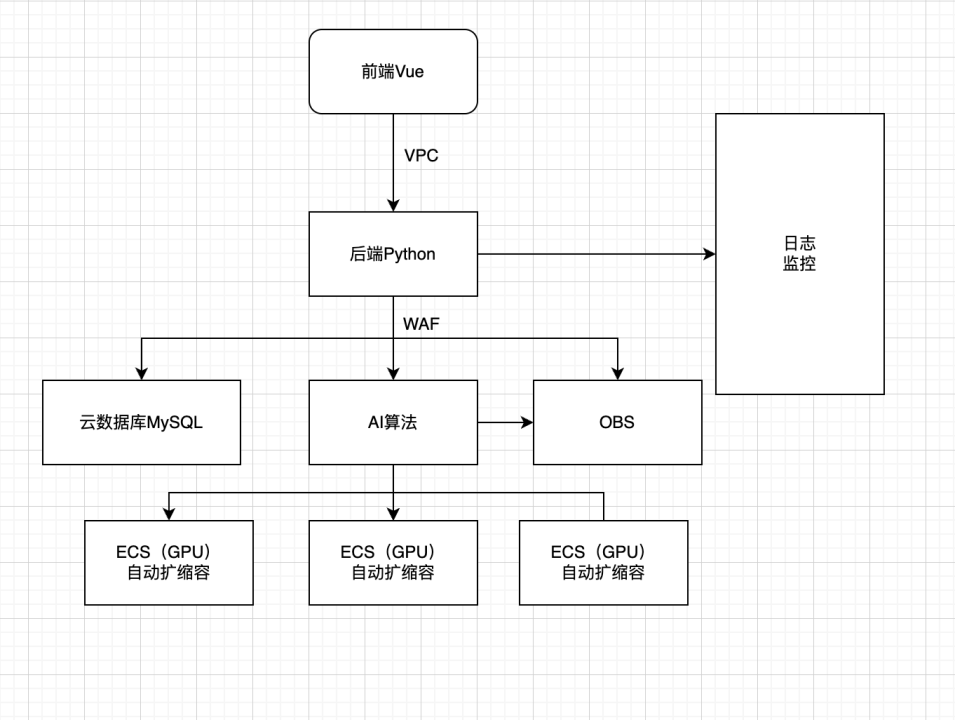
ImgPlus:基于CodeFormer的图片增强
背景 最近参与了华为云开发者大会AI赛道,做了一个AI图片增强作品,本片文章来简单介绍一下。 正文 作品名称:ImgPlus 赛题技术领域选择: AI,图片增强 使用技术名称: CodeFormer,ECS࿰…...
)
2024华为校招面试真题汇总及其解答(二)
6.【算法题】三步问题 题目: 三步问题。有个小孩正在上楼梯,楼梯有n阶台阶,小孩一次可以上1阶、2阶或3阶。实现一种方法,计算小孩有多少种上楼梯的方式。结果可能很大,你需要对结果模1000000007。 示例1: 输入:n = 3 输出:4说明: 有四种走法示例2: 输入:n = 5输出:1…...
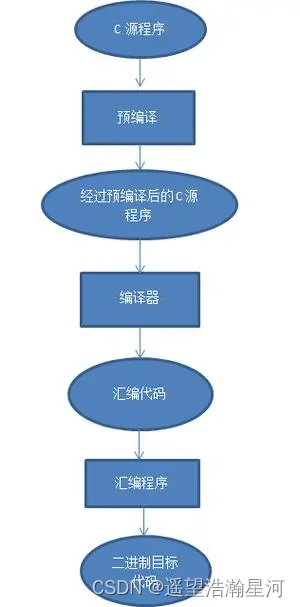
编译链接(Compile Link)
文章目录 前言一、翻译环境1、概念2、翻译环境的组成3、什么是编译链接? 二、编译1、编译的阶段2、预编译3、编译1、什么是语法分析?2、什么是词法分析?3、什么是语义分析?4、什么是符号汇总? 4、汇编1、符号表展示 三…...

14 幂等生产者和事务生产者
kafka消息交付可靠性保障和精确一次语义处理 消息交付可靠性保障,指的kafka对Producer和Consumer要处理的消息提供什么样的承诺。总共就三种:at most once 、at least once、axactly once kafka默认提供的是 at least once。原因是只有Broker提交消息并…...

zabbix部署与监控
目录 一、什么是zabbix? 二、zabbix 监控原理 三、Zabbix 新特性 三、Zabbix 功能组件 四、部署 zabbix zabbix的服务端部署 zabbix的客户端部署 zabbix的服务端部署 一、什么是zabbix? zabbix 是一个基于 Web 界面的提供分布式系统监视以及网络…...

Python 编程基础 | 第五章-类 | 5.8、运算符重载
一、运算符重载 1、Python类内置方法 Python常用内置方法,如下: __init__: 构造函数,在生成对象时调用__del__: 析构函数,释放对象时使用__repr__: 打印,转换__setitem__࿱…...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility 1. 实验室环境1.1 实验室环境1.2 小测试 2. The Endor System2.1 部署应用2.2 检查现有策略 3. Cilium 策略实体3.1 创建 allow-all 网络策略3.2 在 Hubble CLI 中验证网络策略源3.3 …...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

【SQL学习笔记1】增删改查+多表连接全解析(内附SQL免费在线练习工具)
可以使用Sqliteviz这个网站免费编写sql语句,它能够让用户直接在浏览器内练习SQL的语法,不需要安装任何软件。 链接如下: sqliteviz 注意: 在转写SQL语法时,关键字之间有一个特定的顺序,这个顺序会影响到…...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...

NXP S32K146 T-Box 携手 SD NAND(贴片式TF卡):驱动汽车智能革新的黄金组合
在汽车智能化的汹涌浪潮中,车辆不再仅仅是传统的交通工具,而是逐步演变为高度智能的移动终端。这一转变的核心支撑,来自于车内关键技术的深度融合与协同创新。车载远程信息处理盒(T-Box)方案:NXP S32K146 与…...

2025年渗透测试面试题总结-腾讯[实习]科恩实验室-安全工程师(题目+回答)
安全领域各种资源,学习文档,以及工具分享、前沿信息分享、POC、EXP分享。不定期分享各种好玩的项目及好用的工具,欢迎关注。 目录 腾讯[实习]科恩实验室-安全工程师 一、网络与协议 1. TCP三次握手 2. SYN扫描原理 3. HTTPS证书机制 二…...

MacOS下Homebrew国内镜像加速指南(2025最新国内镜像加速)
macos brew国内镜像加速方法 brew install 加速formula.jws.json下载慢加速 🍺 最新版brew安装慢到怀疑人生?别怕,教你轻松起飞! 最近Homebrew更新至最新版,每次执行 brew 命令时都会自动从官方地址 https://formulae.…...
