Vue-3.1缓存组件keep-alive
问题:从首页卡片点到详情页,又点返回,数据重新加载了->希望回到原来的位置
原因:路由跳转后,组件被销毁了,返回回来组件又被重建了,所以数据重新被加载了
解决:利用keep-alive将组件缓存下来
keep-alive是什么
keep-alive是Vue的内置组件,当它包裹动态组件时,会缓存不活动的组件实例,而不是销毁它们。
keep-alive是一个抽象组件:它自身不会渲染成一个DOM元素,也不会出现在父组件链中,只是一个容器。
keep-alive的优点
在组件切换过程中把切换出去的组件保留在内存中,防止重复渲染DOM,减少加载时间及性能消耗,提高用户体验性。
<template><div class="h5-wrapper"><keep-alive><router-view></router-view></keep-alive></div>
</template>问题:缓存了所有被切换的组件
keep-alive是三个属性
1)include:组件名数组,只有匹配的组件会被缓存
2)exclude:组件名数组,任何匹配的组件都不会被缓存
3)max:最多可以缓存多少组件实例
<template><div class="h5-wrapper" :include="['LayoutPage']"><keep-alive><router-view></router-view></keep-alive></div>
</template>组件名:name命名的,如果没有配置name,才会找文件名作为组件名
被缓存的组件会多两个生命周期钩子
1)actived:激活时,组件被看到时触发->进入页面时触发
2)deactived:失活时,组件看不见时触发->离开页面时触发
组件缓存了,就不会执行组件的created、mounted、destroyed等钩子,所以提供了actived和deactived
相关文章:

Vue-3.1缓存组件keep-alive
问题:从首页卡片点到详情页,又点返回,数据重新加载了->希望回到原来的位置 原因:路由跳转后,组件被销毁了,返回回来组件又被重建了,所以数据重新被加载了 解决:利用keep-alive将…...
14.8 Socket 一收一发通信
通常情况下我们在编写套接字通信程序时都会实现一收一发的通信模式,当客户端发送数据到服务端后,我们希望服务端处理请求后同样返回给我们一个状态值,并以此判断我们的请求是否被执行成功了,另外增加收发同步有助于避免数据包粘包…...

7天狂揽 1.3w star 的 MetaGPT,他们的目标让软件公司为之一惊
在 AI 产品爆炸的今天,拥有各种本领的 AI 产品层出不穷,但 MetaGPT 的出现仍然显的格外耀眼,其可以实现只输入单一 prompt,就可以输出需求分析、需求文档、技术架构、最终代码等等产物,这相当于一个开发团队的输出成果…...

工控网络协议模糊测试:用peach对modbus协议进行模糊测试
0x00 背景 本人第一次在FB发帖,进入工控安全行业时间不算很长,可能对模糊测试见解出现偏差,请见谅。 在接触工控安全这一段时间内,对于挖掘工控设备的漏洞,必须对工控各种协议有一定的了解,然后对工控协议…...

python+opencv+机器学习车牌识别 计算机竞赛
0 前言 🔥 优质竞赛项目系列,今天要分享的是 🚩 基于机器学习的车牌识别系统 🥇学长这里给一个题目综合评分(每项满分5分) 难度系数:4分工作量:4分创新点:3分 该项目较为新颖,适…...

魔域服务端数据库说明
Magic.DB MagID: 魔法ID Mag:Magic MagName: 魔法名称 EffectType: 效果类型 Effect: 效果 Spell: 魔力(魔法值) Power: 能力,力量 MaxPower: 最大能力 DefSpell: 变化后的魔力Def:deformation DefPower: 变化后能力 DefMaxPower:…...
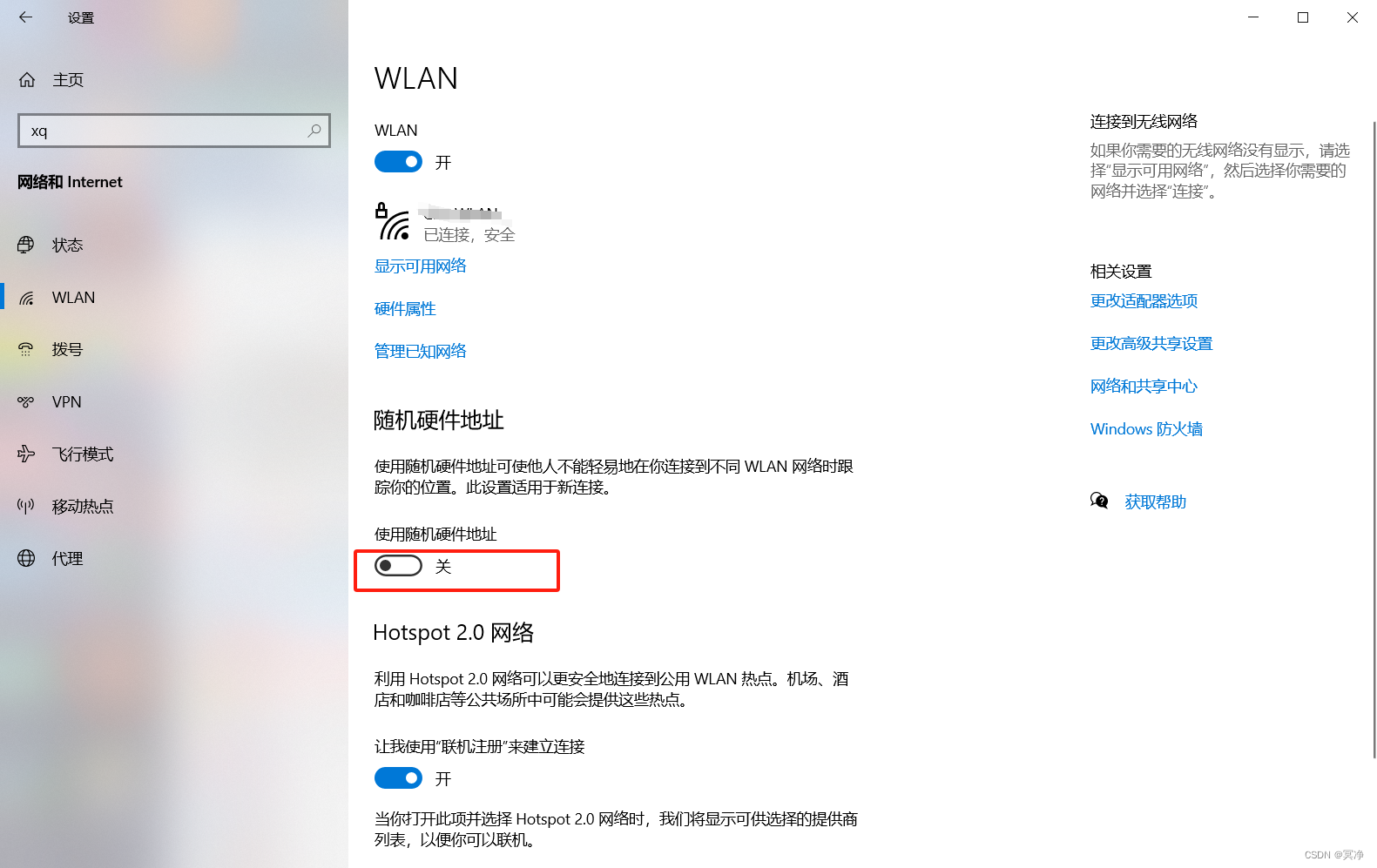
笔记本无线网卡MAC一直改动
今天在网管处把我无线网卡的MAC地址添加后,回来链接无线网却一直显示网络链接失败,以为是自己的驱动问题,去官网下载了最新的驱动结果依然无法链接。之前在家或者公共场合链接WiFi从来没有出现过类似情况。 百思不得其解之际发现自己的无线网…...
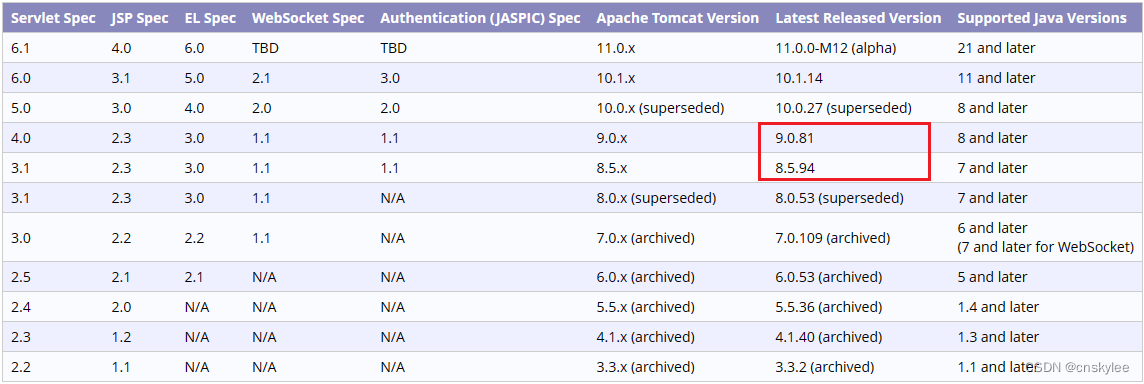
【Tomcat】Apache发布两个新版本Tomcat修复多个Bug
Apache 官网发布了两个最新的 Tomcat 版本包,分别是:8.5.94、9.0.81 这两个最新版本修复了多个漏洞,统计信息如下表所示。有关漏洞的详细信息,请查阅官方相关文档(见:参考)。 严重等级漏洞说明…...
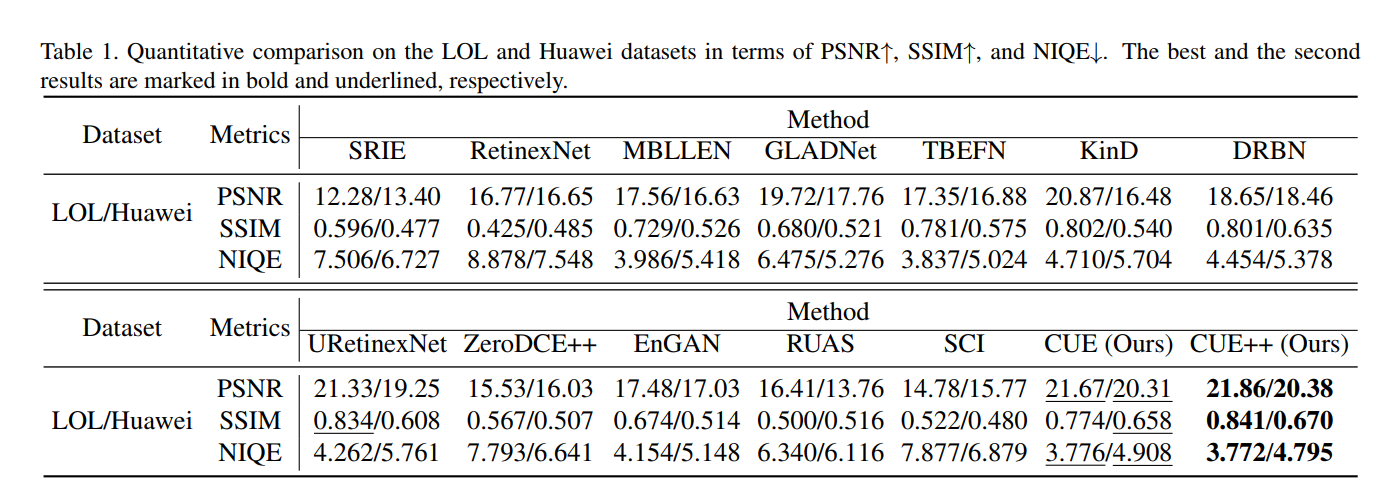
Empowering Low-Light Image Enhancer through Customized Learnable Priors 论文阅读笔记
中科大、西安交大、南开大学发表在ICCV2023的论文,作者里有李重仪老师和中科大的Jie Huang(ECCV2022的FEC CVPR2022的ENC和CVPR2023的ERL的一作)喔,看来可能是和Jie Huang同一个课题组的,而且同样代码是开源的…...

LeetCode 2652. 倍数求和【数学,容斥原理】简单
本文属于「征服LeetCode」系列文章之一,这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁,本系列将至少持续到刷完所有无锁题之日为止;由于LeetCode还在不断地创建新题,本系列的终止日期可能是永远。在这一系列刷题文章…...

ansible-playbook剧本
一,playbook组成: (1)Tasks:任务,即通过 task 调用 ansible 的模板将多个操作组织在一个 playbook 中运行 (2)Variables:变量 (3)Templates&…...
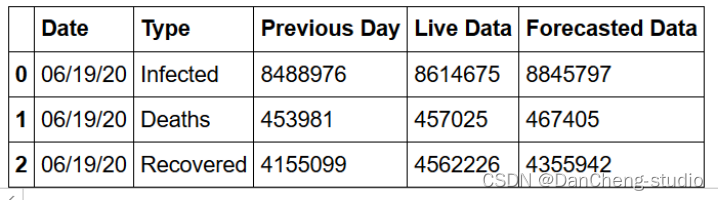
竞赛选题 深度学习LSTM新冠数据预测
文章目录 0 前言1 课题简介2 预测算法2.1 Logistic回归模型2.2 基于动力学SEIR模型改进的SEITR模型2.3 LSTM神经网络模型 3 预测效果3.1 Logistic回归模型3.2 SEITR模型3.3 LSTM神经网络模型 4 结论5 最后 0 前言 🔥 优质竞赛项目系列,今天要分享的是 …...

机械设计师应该在工作中培养哪些良好习惯?
图纸规范 1、一定要按照制图标准设计图纸!图纸上任何一条直线(无论是点划线、粗实线、细实线等等)、数值、公差、图标等,都必须有理有据,不能想当然。图纸是产品生产的基础,无论是生产、加工、装配&#x…...

小程序新增功能页面
需求背景: 小程序主页面有个报名板块,我打算替换主页面报名板块菜单,迁移到我的页面里面, 替换成资讯栏目,我喜欢分享最新技术,开源课题,IT资讯,本想做成论坛的效果,由于时间问题,先替换添加板块 替换后效果: 模块功能: 添加、修改、删除、查看 文件目录:// 添…...

LeetCode每日一题——2652. Sum Multiples
文章目录 一、题目二、题解 一、题目 Given a positive integer n, find the sum of all integers in the range [1, n] inclusive that are divisible by 3, 5, or 7. Return an integer denoting the sum of all numbers in the given range satisfying the constraint. E…...
)
Python问答题(更新中)
1. 列表(list)和元组(tuple)有什么区别? 列表是可变的,创建后可以对其进行修改;元组是不可变的,元组一旦创建,就不能对其进行更改。列表表示的是顺序。它们是有序序列&a…...

服务器中了locked勒索病毒怎么办,勒索病毒解密,数据恢复
最近一段时间内,相信很多使用金蝶或用友的办公软件的企业,有很多都经历了locked勒索病毒的攻击,导致企业服务器被加密无法正常使用,严重影响了企业的正常工作。通过云天数据恢复中心的解密恢复发现,在今年locked勒索病…...

游游的字母串 (环形数组两点之间的位置)
题目链接:登录—专业IT笔试面试备考平台_牛客网 题目: 样例: 输入 yab 输出 3 思路: 暴力枚举,全部变成对应的26个字母字符需要的操作步数,取最少的一个操作步数, 这里的操作步数࿰…...
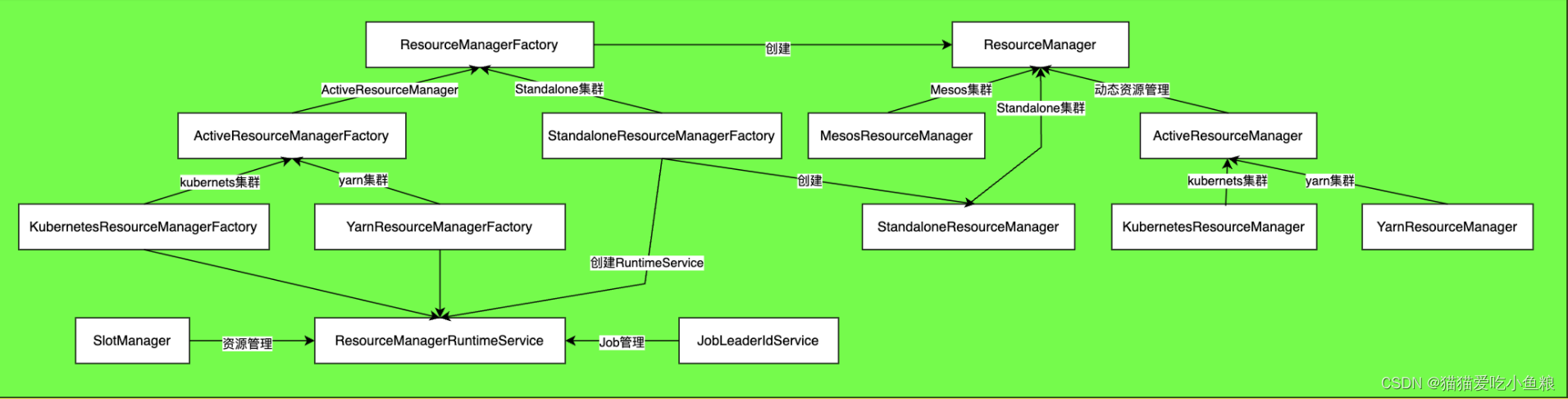
Flink的ResourceManager详解(一)
ResourceManager 总结 一、概述 1、ResourceManager 管理 Flink 集群中的计算资源,计算资源主要来自 TaskManager 组件。 2、如果集群采用 Native【本地模式】部署,则 ResourceManager 会动态地向集群资源管理器申请 Container 并启动TaskManager&…...

Tornado 可以使用 nginx 提供负载均衡
Tornado和nginx都是网络服务器的重要组成部分,但它们在职能和使用场景上存在显著的差异。 Tornado可以独立运行,而不需要依赖nginx等其他Web服务器。这是因为Tornado本身就是一个完整的Web服务器,可以独立处理HTTP请求并返回响应数据。 ngi…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

【杂谈】-递归进化:人工智能的自我改进与监管挑战
递归进化:人工智能的自我改进与监管挑战 文章目录 递归进化:人工智能的自我改进与监管挑战1、自我改进型人工智能的崛起2、人工智能如何挑战人类监管?3、确保人工智能受控的策略4、人类在人工智能发展中的角色5、平衡自主性与控制力6、总结与…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...

【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控,故障处理工具
第2章 虚拟机性能监控,故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令:jps [options] [hostid] 功能:本地虚拟机进程显示进程ID(与ps相同),可同时显示主类&#x…...

BLEU评分:机器翻译质量评估的黄金标准
BLEU评分:机器翻译质量评估的黄金标准 1. 引言 在自然语言处理(NLP)领域,衡量一个机器翻译模型的性能至关重要。BLEU (Bilingual Evaluation Understudy) 作为一种自动化评估指标,自2002年由IBM的Kishore Papineni等人提出以来,…...
零知开源——STM32F103RBT6驱动 ICM20948 九轴传感器及 vofa + 上位机可视化教程
STM32F1 本教程使用零知标准板(STM32F103RBT6)通过I2C驱动ICM20948九轴传感器,实现姿态解算,并通过串口将数据实时发送至VOFA上位机进行3D可视化。代码基于开源库修改优化,适合嵌入式及物联网开发者。在基础驱动上新增…...
实现跳一跳小游戏)
鸿蒙(HarmonyOS5)实现跳一跳小游戏
下面我将介绍如何使用鸿蒙的ArkUI框架,实现一个简单的跳一跳小游戏。 1. 项目结构 src/main/ets/ ├── MainAbility │ ├── pages │ │ ├── Index.ets // 主页面 │ │ └── GamePage.ets // 游戏页面 │ └── model │ …...

Python训练营-Day26-函数专题1:函数定义与参数
题目1:计算圆的面积 任务: 编写一个名为 calculate_circle_area 的函数,该函数接收圆的半径 radius 作为参数,并返回圆的面积。圆的面积 π * radius (可以使用 math.pi 作为 π 的值)要求:函数接收一个位置参数 radi…...
