图形编辑器:拖拽阻塞优化
大家好,我是前端西瓜哥。在图形编辑器中,想象这么一个场景,我们撤销了一些重要的操作,然后想选中一个图形,看看它的属性。你点了上去,然后你发现你再也无法重做了。
你以为你点了一下,但其实你点击的时候,鼠标还是小小移动了一点,飘了一个像素点。对编辑器来说,它识别到让图形移动一个像素点的操作,就生成了一个新的版本,然后重做栈(redoStack)被清空了,你退回前的操作就没了。
为了解决这类用户微小操作的问题,我们可以巧妙地给拖拽行为加一个 阻塞阈值。具体就是就是按下鼠标后,移动鼠标的距离要大于某个值,我们才认为发生了拖拽,并执行对应工具的逻辑。
下面为我们要实现的效果。此处为了更好地演示效果,将阈值设置得很大。通常设置个 4px 就够了。
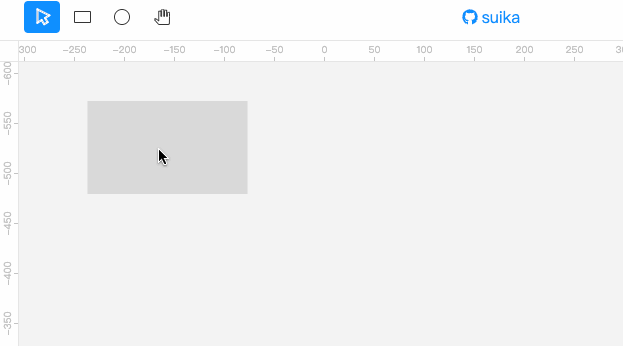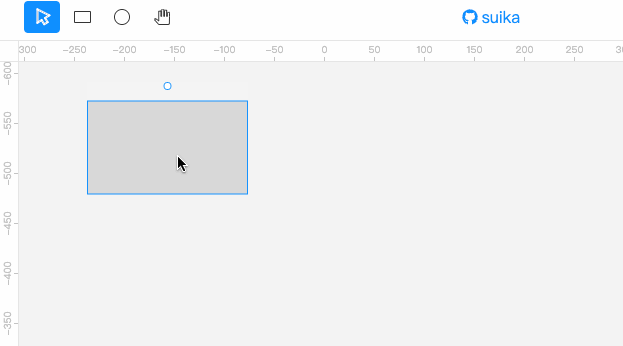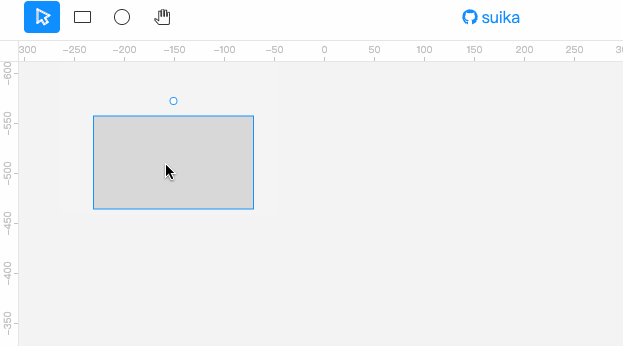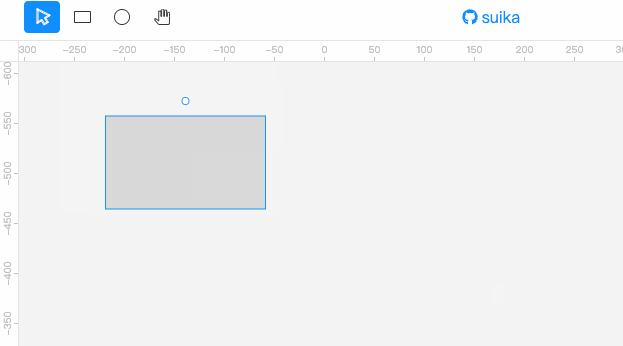
可以看到,按下鼠标然后移动,如果移动的位移太小,矩形是不会被移动的,直到达到一定位移阈值后,矩形才会乖乖听话跟随鼠标进行移动。
阈值表示位移距离,使用的是视口坐标系,而不是场景坐标系。
代码改造
原来的逻辑:
let isPressing = false;
let currentTool = null; // 当前工具对象// 鼠标按下
function handleDown(e) {isPressing = true;currentTool.start(e);
}// 鼠标移动
function handleMove(e) {if (isPressing) {currentTool.drag(e);} else {// 非拖拽的移动事件// 比如选择工具停留在图形上,图形要高亮,此时没发生拖拽currentTool.move(e);}
}// 鼠标释放
function handleUp(e) {currentTool.end(e);isPressing = false;
}
鼠标按下时,isPressing 设置为 true,表示发生了鼠标按下事件。
此时鼠标再移动,我们就能知道这是一个 “拖拽” 的行为,即按下鼠标不放然后移动鼠标的行为。此时调用工具对象的 drag 方法。
最后鼠标释放,将状态 isPressing 重置。
现在我们进行改造。
let isPressing = false;
let currentTool = null; // 当前工具对象let isEnableDragging = false; // 是否调用工具对象的 drag 方法
let startPos = null; // 保存鼠标按下时的坐标
const blockStep = 4; // 阈值function handleDown(e) {isPressing = true;isEnableDragging = false;startPos = { x: e.clientX, y: e.clientY };currentTool.start(e);
}function handleMove(e) {// 判断位移是否突破阈值,是的话更新状态为 “可拖拽”if (!isEnableDragging &&(Math.abs(e.clientX - startPos.x) > blockStep ||Math.abs(e.clientX - startPos.x) > blockStep)) {isEnableDragging = true;}if (isPressing) {if (isEnableDragging) {// “可拖拽” 状态,调用工具的 drag 方法currentTool.drag(e);}} else {currentTool.move(e);}
}function handleUp(e) {currentTool.end(e);// 初始化状态isPressing = false;isEnableDragging = false;startPos = null;
}核心思路是引入 isEnableDragging 状态,表示鼠标移动时,是否达到移动的条件。
我们在鼠标移动事件中,计算鼠标按下和鼠标移动之间的距离是否超过某个值,如果超过阈值,就将 isEnableDragging 状态转换为 true。
然后判断 isEnableDragging 为 true,就调用工具对象的 drag 方法。
需要注意的是,不要只用位移距离来判断是否可以拖拽,要配合状态。否则突破阈值后,又移动回来,你会发现你又卡住了,因为此时阈值因为再次计算,没能达到阈值。
所以加了个 isEnableDragging 状态,在第一次突破阈值设置为 true 后,就再也不用计算位移了,之后一直都是可拖拽状态,直到鼠标释放重置状态。
结尾
拖拽阻塞是开发图形编辑器的一点小细节,并不复杂,但能带来很好的用户体验。
我是前端西瓜哥,欢迎关注我,学习更多前端知识。
相关文章:

图形编辑器:拖拽阻塞优化
大家好,我是前端西瓜哥。在图形编辑器中,想象这么一个场景,我们撤销了一些重要的操作,然后想选中一个图形,看看它的属性。你点了上去,然后你发现你再也无法重做了。 你以为你点了一下,但其实你…...

c++ 的 Eigen库写 AX=XB的矩阵求解代码
1.AXXB的矩阵求解代码(3*3) #include <iostream> #include <Eigen/Dense>int main() {// 定义矩阵A和BEigen::MatrixXd A(3, 3);A << 1, 2, 3,4, 5, 6,7, 8, 9;Eigen::MatrixXd B(3, 3);B << 10, 11, 12,13, 14, 15,16, 17, 18;// 求解AXXBEigen::Mat…...
正点原子linux驱动篇
linux驱动开发与裸机开发的区别 裸机直接操作寄存器,有些mcu提供了库,但还是很底层 1、linux驱动开发直接操作寄存器很麻烦不现实,主要是根据linux驱动框架进行开发(就是有很多操作都是一样的,我们只需要对一个程序模…...

MATLAB绘制雷达图/蜘蛛图
雷达图/蜘蛛图 1 方法一 函数来源为MATLAB | 如何使用MATLAB绘制雷达图(蜘蛛图) 1.1 调用函数 1.2 案例 2 方法二 函数来源为MATLAB帮助-spider_plot 2.1 调用函数 语法(Syntax): spider_plot(P)spider_plot(P, Name, Value, ...)h …...

算法入门,十字路口选择的案例,如果是南方,则向前行
从if判断start; 十字路口的案例 class HelloWorld { static void Main(string[] args) { /* Write C# code in this online editor and run it. */ Console.WriteLine("Hello World!"); string f…...
父传子与子传父步骤
父传子: 问题:父页面中引入子组件 把想要传给子页面的值用在子组件中用 :值“值” (用同一个值好区分)来绑定。 在子页面中用props接收 子组件不能改变父组件传过来的值。(传多个页面的时候是,比如父传孙的时候我会…...

Java concurrency - Task Execution
1.在单个线程里处理所有的请求:接受请求-处理请求 优点:逻辑简单 缺点:吞吐量低,资源利用率低,响应时间长 2.每个任务分配一个单独的线程来处理: 接受请求-创建线程-在线程里处理请求 优点: …...

浅谈BOM
什么是BOM BOM对于每个前端都不陌生,但是很多人都停留在表面,而没有深层次的研究过它。JavaScript有一个非常重要的运行环境就是浏览器,而且浏览器本身又作为一个应用程序需要对其本身进行操作,所以通常浏览器会有对应的对象模型…...

每日学术速递2.24
CV - 计算机视觉 | ML - 机器学习 | RL - 强化学习 | NLP 自然语言处理 Subjects: cs.LG 1.BUAA_BIGSCity: Spatial-Temporal Graph Neural Network for Wind Power Forecasting in Baidu KDD CUP 2022 标题:BUAA_BIGSCity:百度KDD CUP 2022风电预测…...
)
SpringBoot 面试问答总结(VIP典藏版)
1. 什么是 Spring Boot? Spring Boot 是 Spring 开源组织下的子项目,是 Spring 组件一站式解决方案,主要是简化了使用Spring 的难度, 简省了繁重的配置,提供了各种启动器,使开发者能快速上手。 2. 为什…...

CSS 定位网页元素【快速掌握知识点】
目录 前言 一、position: static 二、position: relative 三、position: absolute 四、position: fixed 五、position: sticky 前言 当我们在设计网页时,经常需要对网页中的元素进行定位,以便它们出现在我们想要的位置。在 CSS 中,我们…...
)
构建Docker基础镜像(ubuntu20.04+python3.7.1+chrome101+chromedriver101)
文章目录 一、前置条件1.下载 chrome【google-chrome-stable_current_amd64.deb】2.下载 chromedriver【chromedriver_linux64.zip】3.创建 ubuntu 镜像源文件【sources.list】二、构建方法1.构建目录1.创建DockerFile2.打包镜像一、前置条件 要先下载一个支持 linux 的 浏览器…...
最新最全Java面试知识
工作也有好些年了,从刚毕业到前几年看过无数的面试题,在这个过程中也作为面试官面试过其他人,总想着自己写一个面试总结,随着自我认识的变化,一些知识点的理解也越来越不一样了。写下来温故而知新。很多问题可能别人也…...

个人电脑需求严重疲软,联想集团财务前景仍不乐观
来源:猛兽财经 作者:猛兽财经 财务业绩 联想集团(00992)于2月16日盘后公布了2023财年第三季度财报。 财报显示联想集团2023年第三季度的收入为152.67亿美元,从2022年第三季度的2011.27亿美元下降了24.1%。这也导致该公…...

软件测试面试在简历上写了“精通”后,拥有工作经验的我被面试官问到窒息...
前言 如果有真才实学,写个精通可以让面试官眼前一亮! 如果是瞎写?基本就要被狠狠地虐一把里! 最近在面试,我现在十分后悔在简历上写了“精通”二字… 先给大家看看我简历上的技能列表: 熟悉软件测试理…...

色环电容读数方法要点总结
🏡《总目录》 目录 1,概述2,读数方法3,颜色对照表3.1,颜色与电容值数字对照关系表3.2,颜色与10的指数数字对照关系表3.3,颜色与误差对照关系表4,总结1,概述 本文简单介绍色环电容的读数方法。 2,读数方法 如下图所示色环电容共有四个色环。最粗的被命名为第1环,依次…...
C++函数新思想和标准的输入和输出
欢迎来观看温柔了岁月.c的博客目前设有C学习专栏C语言项目专栏数据结构与算法专栏目前主要更新C学习专栏,C语言项目专栏不定时更新待C专栏完毕,会陆续更新C项目专栏和数据结构与算法专栏一周主要三更,星期三,星期五,星…...
)
华为OD机试真题Java实现【汽水瓶】真题+解题思路+代码(20222023)
汽水瓶 有这样一道智力题:“某商店规定:三个空汽水瓶可以换一瓶汽水。小张手上有十个空汽水瓶,她最多可以换多少瓶汽水喝?”答案是 5 瓶,方法如下:先用 9 个空瓶子换3瓶汽水,喝掉 3 瓶满的,喝完以后 4 个空瓶子,用 3 个再换一瓶,喝掉这瓶满的,这时候剩 2 个空瓶子。…...
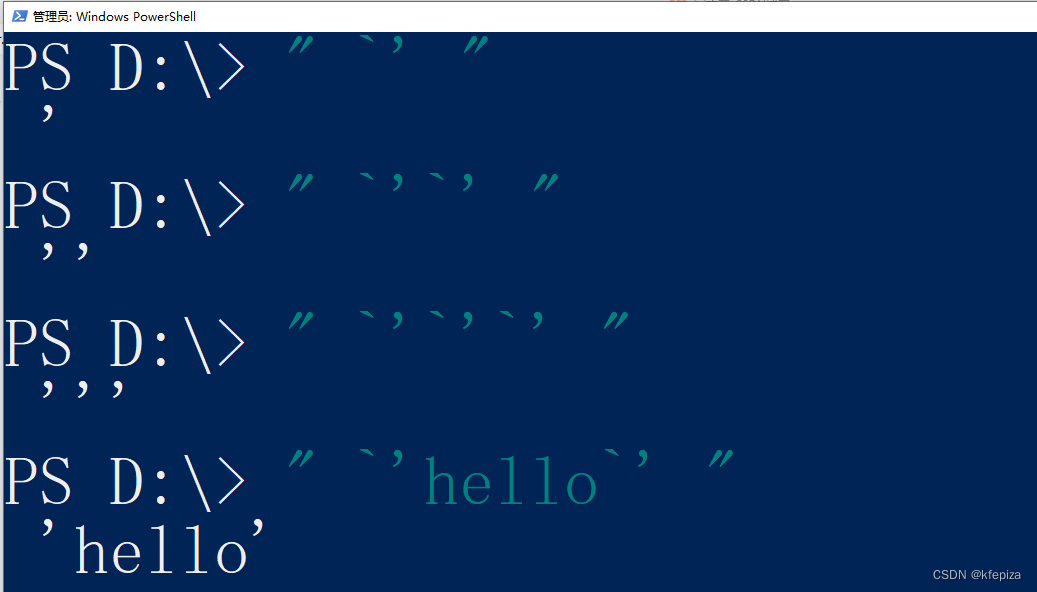
WindownsPowershell中的单引号和双引号
WindownsPowershell中的单引号和双引号 目录标题WindownsPowershell中的单引号和双引号单引号对中,可以直接写双引号双引号对中,可以直接写单引号反引号 可以在 双引号对中表示转义双引号对中, 可以用 反引号双引号 表示一个双引号双引号对中, 可以用 反引号单引号 表示一个单引…...

【华为OD机试模拟题】用 C++ 实现 - 数组组成的最小数字(2023.Q1)
最近更新的博客 华为OD机试 - 入栈出栈(C++) | 附带编码思路 【2023】 华为OD机试 - 箱子之形摆放(C++) | 附带编码思路 【2023】 华为OD机试 - 简易内存池 2(C++) | 附带编码思路 【2023】 华为OD机试 - 第 N 个排列(C++) | 附带编码思路 【2023】 华为OD机试 - 考古…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...

Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信
文章目录 Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信前言一、网络通信基础概念二、服务端与客户端的完整流程图解三、每一步的详细讲解和代码示例1. 创建Socket(服务端和客户端都要)2. 绑定本地地址和端口&#x…...

【网络安全】开源系统getshell漏洞挖掘
审计过程: 在入口文件admin/index.php中: 用户可以通过m,c,a等参数控制加载的文件和方法,在app/system/entrance.php中存在重点代码: 当M_TYPE system并且M_MODULE include时,会设置常量PATH_OWN_FILE为PATH_APP.M_T…...

多元隐函数 偏导公式
我们来推导隐函数 z z ( x , y ) z z(x, y) zz(x,y) 的偏导公式,给定一个隐函数关系: F ( x , y , z ( x , y ) ) 0 F(x, y, z(x, y)) 0 F(x,y,z(x,y))0 🧠 目标: 求 ∂ z ∂ x \frac{\partial z}{\partial x} ∂x∂z、 …...

【R语言编程——数据调用】
这里写自定义目录标题 可用库及数据集外部数据导入方法查看数据集信息 在R语言中,有多个库支持调用内置数据集或外部数据,包括studentdata等教学或示例数据集。以下是常见的库和方法: 可用库及数据集 openintro库 该库包含多个教学数据集&a…...
