C++数据结构X篇_15_求二叉树叶子数与高度(递归方法)
本篇参考求二叉树叶子数与高度(C++)进行整理。
文章目录
- 1. 二叉树中叶子数与高度
- 2. 求二叉树叶子数与高度的实现代码
1. 二叉树中叶子数与高度
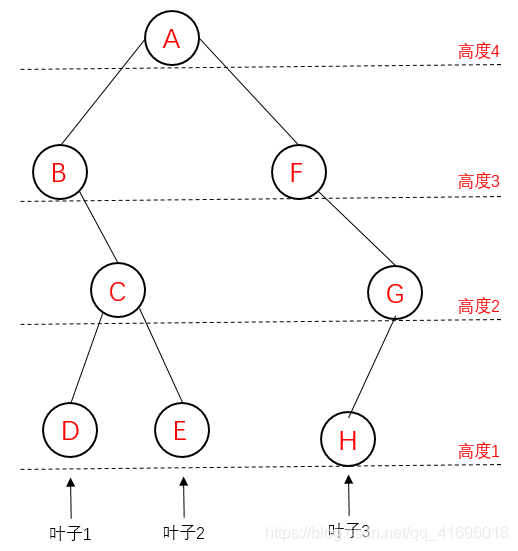
我们首先来看一看二叉树中叶子数与高度的定义:
-
叶子数:对于一个二叉树的节点,若其既没有左子树又没有右子树,那它就是叶子节点。整个二叉树的叶子数为所有叶子节点个数。 -
高度:二叉树高度又称深度,其为根节点到叶子节点路径的最大值。
2. 求二叉树叶子数与高度的实现代码
求二叉树叶子数与高度均采用递归的方法,其基本操作方法都比较类似,具体实现代码如下:
#include <iostream>
using namespace std;
//定义二叉树节点
class binarynode
{
public:char data; //节点数据域binarynode* lchild; //左孩子binarynode* rchild; //右孩子
};
//求树高度
int getheight(binarynode *root)
{if (root == NULL){return 0;}//求左子树高度int lheight = getheight(root->lchild);//求右子树高度int rheight = getheight(root->rchild);//当前节点高度int height = lheight > rheight ? lheight + 1 : rheight + 1;;return height;
}
//求叶子节点,采用递归方法
void calculateleafnum(binarynode* root, int* leafnum)
{if (root == NULL){return;}if (root->rchild == NULL && root->lchild == NULL){(*leafnum)++;}//左子树节点数目calculateleafnum(root->lchild, leafnum);//右子树节点数目calculateleafnum(root->rchild, leafnum);
}
//创建二叉树
void createtree()
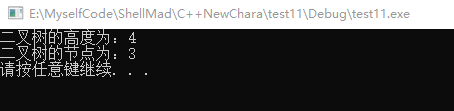
{//创建节点binarynode node1 = { 'A',NULL,NULL };binarynode node2 = { 'B',NULL,NULL };binarynode node3 = { 'C',NULL,NULL };binarynode node4 = { 'D',NULL,NULL };binarynode node5 = { 'E',NULL,NULL };binarynode node6 = { 'F',NULL,NULL };binarynode node7 = { 'G',NULL,NULL };binarynode node8 = { 'H',NULL,NULL };//建立节点关系node1.lchild = &node2;node1.rchild = &node6;node2.rchild = &node3;node3.lchild = &node4;node3.rchild = &node5;node6.rchild = &node7;node7.lchild = &node8;//计算二叉树高度int height = getheight(&node1);cout << "二叉树的高度为:" << height << endl;//计算二叉树叶子数int num = 0;calculateleafnum(&node1, &num);cout << "二叉树的节点为:" << num << endl;
}int main()
{createtree();system("pause");return 0;
}运行结果:
- 求二叉树叶子数与高度
相关文章:

C++数据结构X篇_15_求二叉树叶子数与高度(递归方法)
本篇参考求二叉树叶子数与高度(C)进行整理。 文章目录 1. 二叉树中叶子数与高度2. 求二叉树叶子数与高度的实现代码 1. 二叉树中叶子数与高度 我们首先来看一看二叉树中叶子数与高度的定义: 叶子数:对于一个二叉树的节点&#x…...
MySQL锁学习笔记
锁 事务的隔离性由锁来实现。 概述 锁是计算机协调多个进程或线程并发访问某一资源的机制。在程序开发中会存在多线程同步的问题,当多个线程并发访问某个数据的时候,尤其是针对一些敏感的数据(比如订单、金额等),我…...

如何将前后端分离项目部署到本地的Docker Desktop容器运行并且访问
文章目录 前言 完成了客户的一个前后端分离项目,要求部署到客户电脑上去展示,那肯定不能直接把代码弄上去跑呀~~~,于是我就想把他们都打包部署到本地的docker容器里面,方便运行和访问,so,以下内容就详细介…...
前端开发中的try...catch
首先try...catch 结构可以用来处理 Promise 中的异常。在 JavaScript 中,Promise 提供了一种处理异步操作的机制,并且可以通过 .catch() 方法捕获并处理异步操作中抛出的异常。 async function someAsyncFunction() {try {const result await someProm…...
数据加密中,采用密钥管理系统相比加密机的好处
密钥管理系统与加密机都能提供数据加解密,那么针对具体的应用加密,采用密钥管理系统比单纯使用加密机有哪些优点,列表如下: 集中化管理:密钥管理系统可以对加密算法和密钥进行集中化管理,使得企业可以对加…...
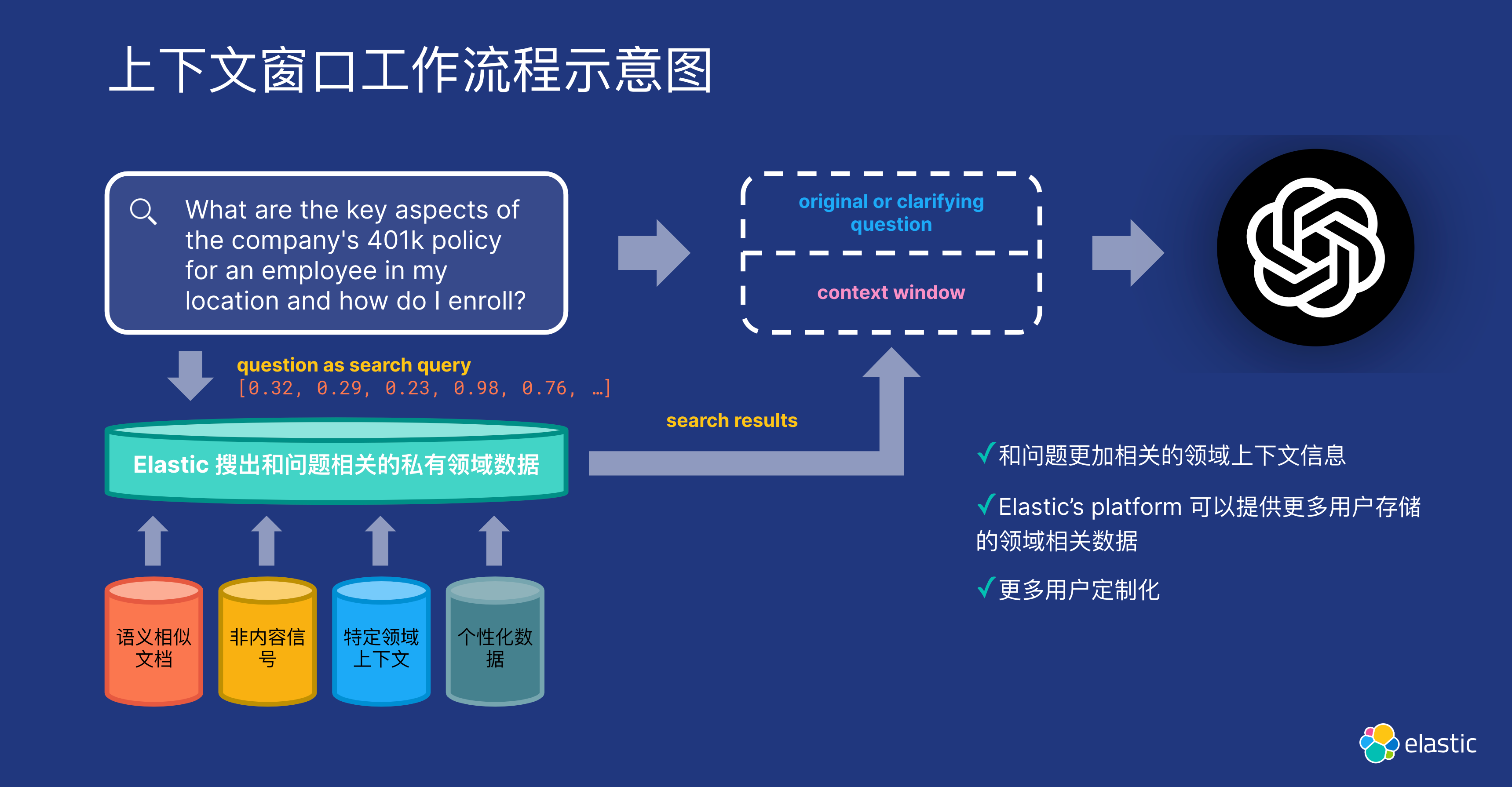
Elasticsearch:什么是大语言模型 (LLMs)?
假设你想参加流行的游戏节目 Jeopardy(这是一个美国电视游戏节目,参赛者将获得答案并必须猜测问题)。 要参加演出,你需要了解任何事情的一切。 所以你决定在接下来的三年里每天都花时间阅读互联网上的所有内容。 你很快就会意识到…...

神奇的python的生成器
函数生成器代码 def num():print("message 1")yield 1print("message 2")yield 2print("message 3")yield 3f num() x next(f) # message 1 print(x) # 输出1x next(f) # message 2 print(x) # 输出2x next(f) # message 3 print(x) …...

【来点小剧场--项目测试报告】个人博客项目自动化测试
前述 针对个人博客项目进行测试,个人博客主要由七个页面构成:注册页、登录页、个人博客列表页、博客发布页、博客修改页、博客列表页、博客详情页,主要功能包括:注册、登录、编辑并发布博客、修改已发布的博客、查看详情、删除博…...

【安卓环境搭建报错的解决】
安卓环境搭建报错的解决 问题描述解决方法 问题描述 电脑中新安装的 Android Studio Giraffe | 2022.3.1 Patch ,运行 studio 系统工程,提示如下错误 Duplicate class kotlin.collections.jdk8.CollectionsJDK8Kt found in modules kotlin-stdlib-1.8.…...

Pruning Pre-trained Language Models Without Fine-Tuning
本文是LLM系列文章,针对《Pruning Pre-trained Language Models Without Fine-Tuning》的翻译。 修剪未微调的预训练语言模型 摘要1 引言2 相关工作3 背景4 静态模型剪枝5 实验6 分析7 结论8 局限性 摘要 为了克服预训练语言模型(PLMs)中的过度参数化问题…...

Java内存模型-Java Memory Model(JMM)-可见性、原子性、有序性
5. Java内存模型之JMM 5.1 先从大场面试开始 你知道什么是Java内存模型JMM吗? JMM和volatile他们两个之间的关系? JMM没有那些特征或者它的三大特征是什么? 为什么要有JMM,它为什么出现?作用和功能是什么…...
基于Springboot实现在线答疑平台系统项目【项目源码+论文说明】
基于Springboot实现在线答疑平台系统演示 摘要 社会的发展和科学技术的进步,互联网技术越来越受欢迎。网络计算机的生活方式逐渐受到广大师生的喜爱,也逐渐进入了每个学生的使用。互联网具有便利性,速度快,效率高,成本…...
)
前端工程化知识系列(1)
目录 1. 什么是前端工程化,以及它为前端开发带来了哪些好处?2. 你使用过哪些版本控制系统?描述一下你在团队中如何处理代码合并和冲突解决的经验。3. 什么是Git,它的工作原理是什么?可以解释一下常用的Git命令吗&#…...
xml文件报错 ORA-00907: 缺失右括号
原来的sql 更改之后 加一个select * from ()...
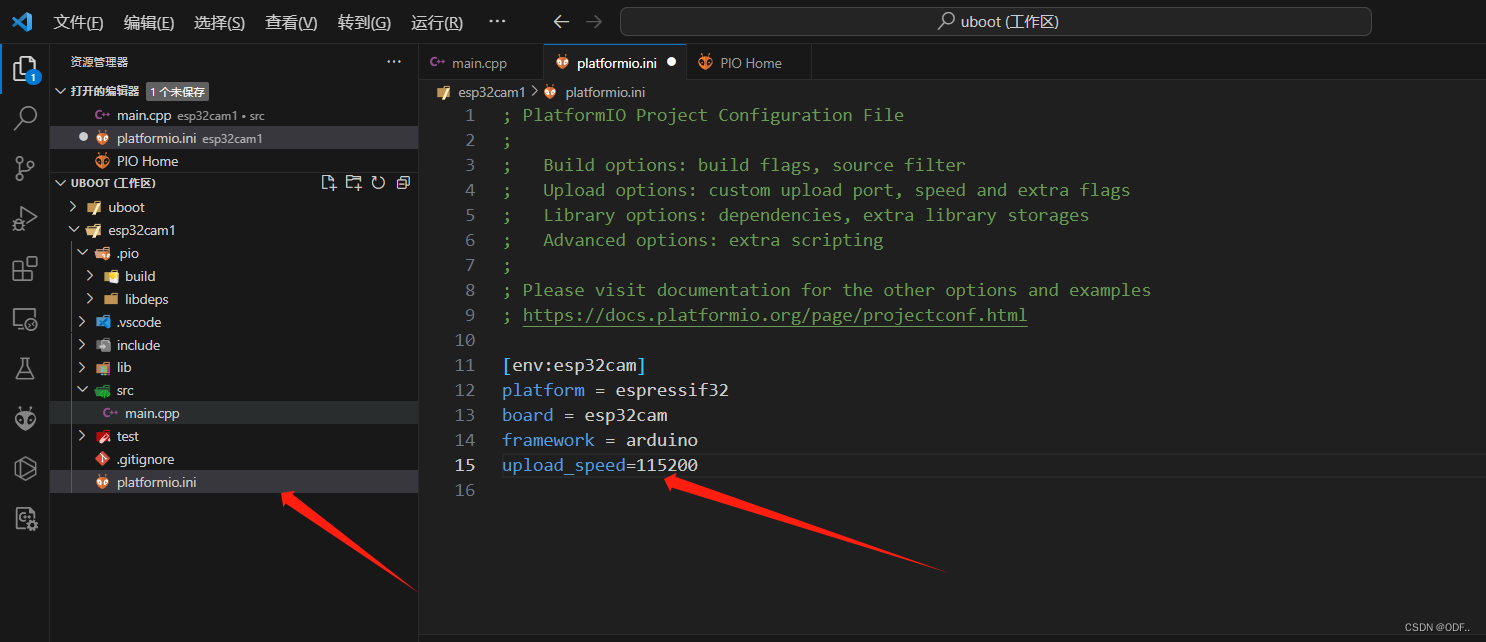
VScode platformio的使用
一、platformio 工程创建 打开vscode界面你会发现左下多了个家的小图标,点击这里就可以进入platformio。 在右侧Quick Access栏中,有4个选项。可以看得出来,我们这里直接点击创建一个新的工程。 点击New Project打开project配置界面&#x…...
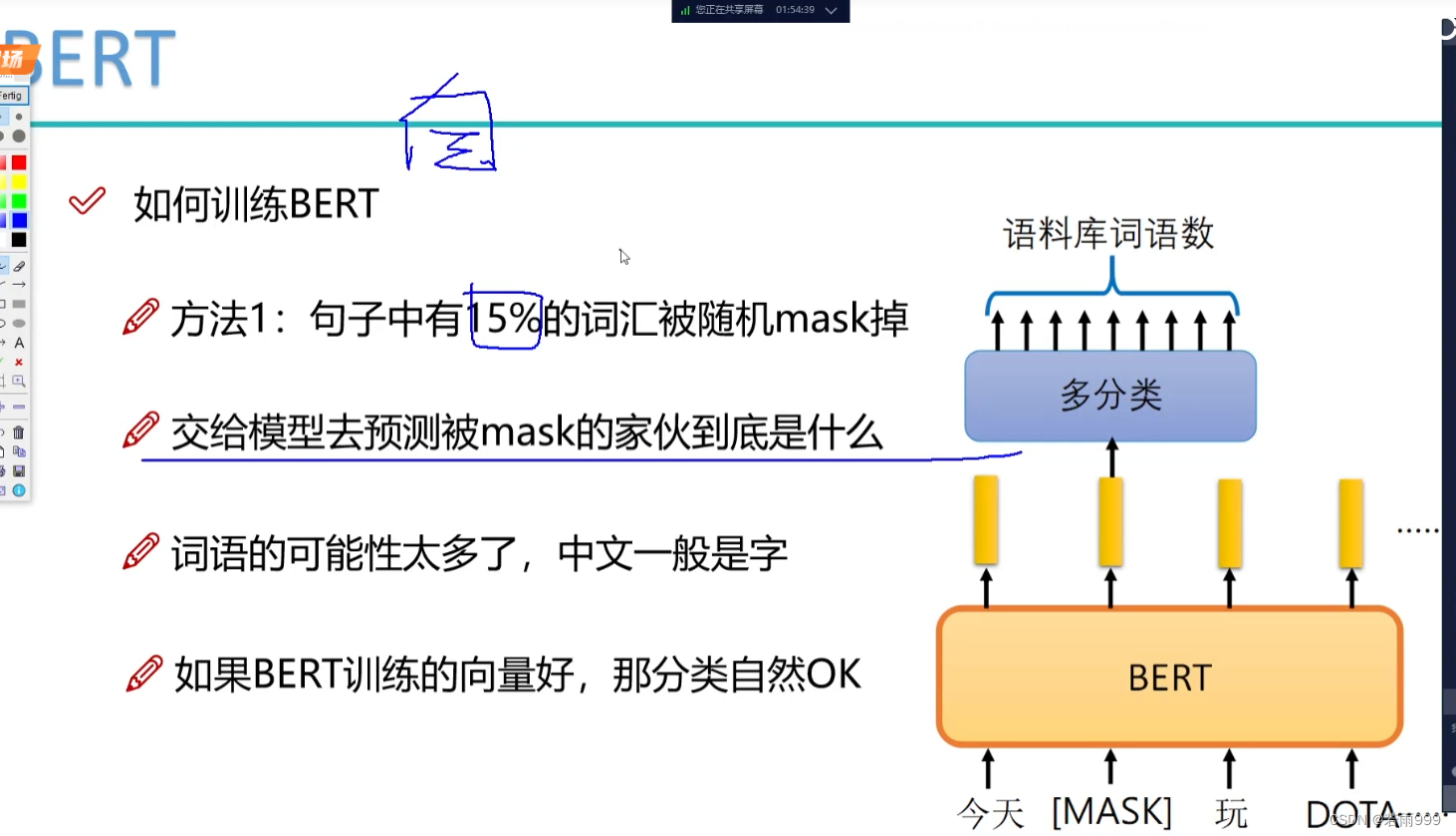
transformer_01
一、传统RNN存在的问题 1.序列前序太长,每个xi要记住前面的特征,而且一直在学,没有忘记,可能特征不能学的太好 2.串行,层越多越慢,难以堆叠很多层; 3.只能看到过去,不能看到未来 搞…...

JavaSE入门---认识方法
文章目录 什么是方法?方法定义实参和形参的关系没有返回值的方法 方法重载方法签名 什么是方法? 在编程中某段功能的代码可能频繁使用到,如果在每个位置都重新实现一遍,会有一些缺点,比如: 使程序变得繁琐…...

编译[Bug]——too few arguments for template template parameter “Tuple“ detected
项目场景: 当使用高版本的cuda去安装低版本pytorch,并且编译用低版本pytorch写的cuda算子时,或者说是VS的版本过高如2022和2019,都有可能会出现某个.h文件或者.c文件报错,如: error: too few arguments f…...

网工内推 | 南天软件,base北京,需持有CCIE认证,最高25k
01 北京南天软件有限公司 招聘岗位:IPT运维工程师 职责描述: 负责客户Cisco语音网络IPT ,CUCM的日常运维,扩容和项目支持,支持路由交换,无线等项目,实施工作以及相关实施文档。 任职要求: 1、…...

Unity有限状态机的简易实现
本人嘴笨,不会说。 该代码实现一个功能较为齐全的有限状态机,可用于大部分的应用场景。 大致实现几个功能 状态更新状态转换状态消息处理全局状态转换和反转状态(转换为前一个状态) 代码分为 状态类状态管理类枚举(…...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

汽车生产虚拟实训中的技能提升与生产优化
在制造业蓬勃发展的大背景下,虚拟教学实训宛如一颗璀璨的新星,正发挥着不可或缺且日益凸显的关键作用,源源不断地为企业的稳健前行与创新发展注入磅礴强大的动力。就以汽车制造企业这一极具代表性的行业主体为例,汽车生产线上各类…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

浅谈不同二分算法的查找情况
二分算法原理比较简单,但是实际的算法模板却有很多,这一切都源于二分查找问题中的复杂情况和二分算法的边界处理,以下是博主对一些二分算法查找的情况分析。 需要说明的是,以下二分算法都是基于有序序列为升序有序的情况…...

3-11单元格区域边界定位(End属性)学习笔记
返回一个Range 对象,只读。该对象代表包含源区域的区域上端下端左端右端的最后一个单元格。等同于按键 End 向上键(End(xlUp))、End向下键(End(xlDown))、End向左键(End(xlToLeft)End向右键(End(xlToRight)) 注意:它移动的位置必须是相连的有内容的单元格…...

2025年渗透测试面试题总结-腾讯[实习]科恩实验室-安全工程师(题目+回答)
安全领域各种资源,学习文档,以及工具分享、前沿信息分享、POC、EXP分享。不定期分享各种好玩的项目及好用的工具,欢迎关注。 目录 腾讯[实习]科恩实验室-安全工程师 一、网络与协议 1. TCP三次握手 2. SYN扫描原理 3. HTTPS证书机制 二…...

站群服务器的应用场景都有哪些?
站群服务器主要是为了多个网站的托管和管理所设计的,可以通过集中管理和高效资源的分配,来支持多个独立的网站同时运行,让每一个网站都可以分配到独立的IP地址,避免出现IP关联的风险,用户还可以通过控制面板进行管理功…...
