排序【七大排序】
文章目录
- 1. 排序的概念及引用
- 1.1 排序的概念
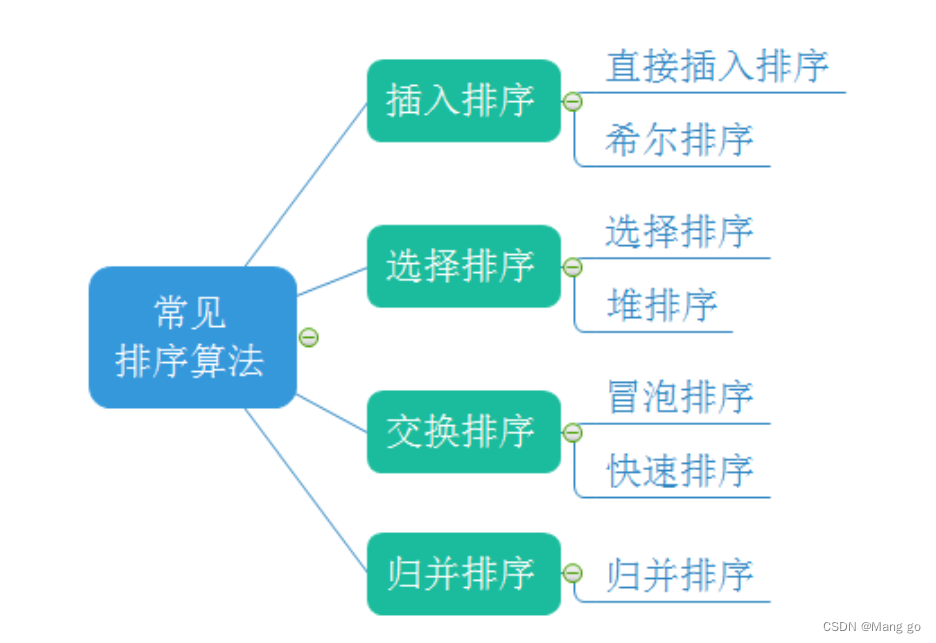
- 1.2 常见的排序算法
- 2. 常见排序算法的实现
- 2.1 插入排序
- 2.1.1基本思想:
- 2.1.2 直接插入排序
- 2.1.3 希尔排序( 缩小增量排序 )
- 2.2 选择排序
- 2.2.1基本思想:
- 2.2.2 直接选择排序:
- 2.2.3 堆排序
- 2.3 交换排序
- 2.3.1冒泡排序
- 2.3.2 快速排序
- 2.4 归并排序
- 2.4.1 基本思想
- 2.4.2 海量数据的排序问题
- 3. 排序算法复杂度及稳定性分析
1. 排序的概念及引用
1.1 排序的概念
排序:所谓排序,就是使一串记录,按照其中的某个或某些关键字的大小,递增或递减的排列起来的操作。
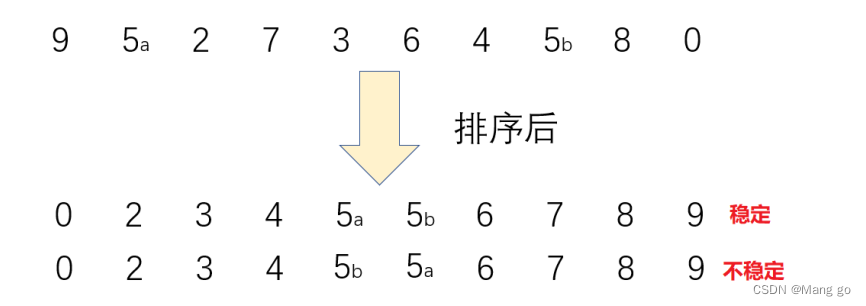
稳定性:假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次序保持
不变,即在原序列中,r[i]=r[j],且r[i]在r[j]之前,而在排序后的序列中,r[i]仍在r[j]之前,则称这种排序算法是稳定的;否则称为不稳定的。
内部排序:数据元素全部放在内存中的排序。
外部排序:数据元素太多不能同时放在内存中,根据排序过程的要求不能在内外存之间移动数据的排序。
1.2 常见的排序算法
2. 常见排序算法的实现
2.1 插入排序
2.1.1基本思想:
直接插入排序是一种简单的插入排序法,其基本思想是:
把待排序的记录按其关键码值的大小逐个插入到一个已经排好序的有序序列中,直到所有的记录插入完为止,得到一个新的有序序列 。实际中我们玩扑克牌时,就用了插入排序的思想。
2.1.2 直接插入排序
当插入第i(i>=1)个元素时,前面的array[0],array[1],…,array[i-1]已经排好序,此时用array[i]的排序码与array[i-1],array[i-2],…的排序码顺序进行比较,找到插入位置即将array[i]插入,原来位置上的元素顺序后移
代码实现
public static void insertSort(int[] array){for (int i = 1; i < array.length; i++) {int tmp = array[i];int j = i-1;for (; j >= 0; j--) {if(array[j] > tmp){array[j+1] = array[j];}else{break;}}array[j+1] = tmp;}}
直接插入排序的特性总结:
- 元素集合越接近有序,直接插入排序算法的时间效率越高
- 时间复杂度:O(N^2)
- 空间复杂度:O(1),它是一种稳定的排序算法
- 稳定性:稳定
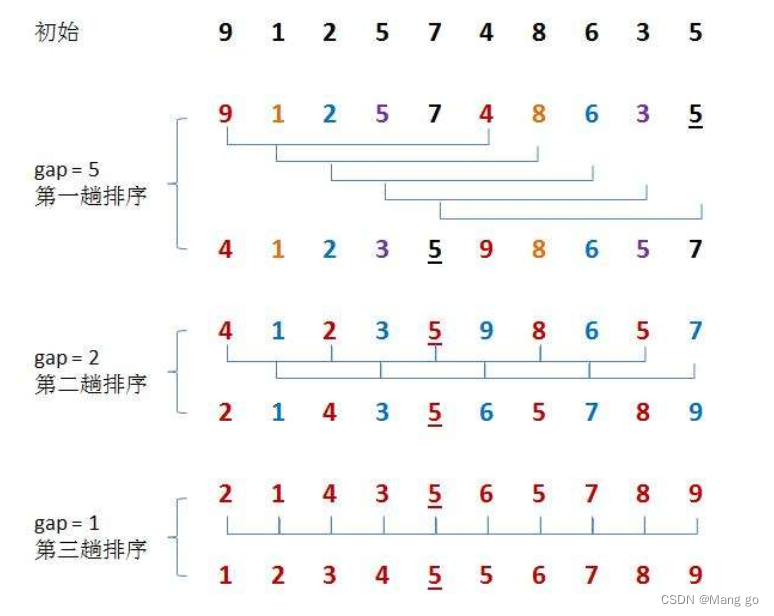
2.1.3 希尔排序( 缩小增量排序 )
希尔排序法又称缩小增量法。希尔排序法的基本思想是:先选定一个整数,把待排序文件中所有记录分成多个组,所有距离为的记录分在同一组内,并对每一组内的记录进行排序。然后,取,重复上述分组和排序的工作。当到达=1时,所有记录在统一组内排好序。
代码实现
public static void hillSort(int[] array){int gap = array.length;while(gap > 1){gap/=2;hill(array,gap);}}public static void hill(int[] array,int gap){for (int i = gap; i < array.length; i++) {int tmp = array[i];int j = i - gap;for (; j >= 0 ; j-=gap) {if(array[j] > tmp){array[j+gap] = array[j];}else {break;}}array[j+gap] = tmp;}}
希尔排序的特性总结:
- 希尔排序是对直接插入排序的优化。
- 当gap > 1时都是预排序,目的是让数组更接近于有序。当gap == 1时,数组已经接近有序的了,这样就会很快。这样整体而言,可以达到优化的效果。我们实现后可以进行性能测试的对比。
- 希尔排序的时间复杂度不好计算,因为gap的取值方法很多,导致很难去计算,因此在好些树中给出的希尔排序的时间复杂度都不固定
- 稳定性:不稳定
2.2 选择排序
2.2.1基本思想:
每一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,直到全部待排序的数据元
素排完 。
2.2.2 直接选择排序:
在元素集合array[i]–array[n-1]中选择关键码最大(小)的数据元素
若它不是这组元素中的最后一个(第一个)元素,则将它与这组元素中的最后一个(第一个)元素交换
在剩余的array[i]–array[n-2](array[i+1]–array[n-1])集合中,重复上述步骤,直到集合剩余1个元素
代码实现:
代码一:
public static void selectSort(int[] array){for (int i = 0; i < array.length; i++) {int min = i;for (int j = i+1; j < array.length; j++) {if(array[j] < array[min]){min = j;}}swap(array,min,i);}}public static void swap(int[] array,int i,int j){int tmp = array[i];array[i] = array[j];array[j] = tmp;}
代码二:
public static void selectSort1(int[] array){int left = 0;int right = array.length-1;while(left < right){int max = left;int min = left;for (int j = left+1; j <= right; j++) {if(array[j] < array[min]){min = j;}if(array[j] > array[max]){max = j;}}swap(array,min,left);if(left == max){max = min;}swap(array,max,right);left++;right--;}}public static void swap(int[] array,int i,int j){int tmp = array[i];array[i] = array[j];array[j] = tmp;}
【直接选择排序的特性总结】
- 直接选择排序思考非常好理解,但是效率不是很好。实际中很少使用
- 时间复杂度:O(N^2)
- 空间复杂度:O(1)
- 稳定性:不稳定
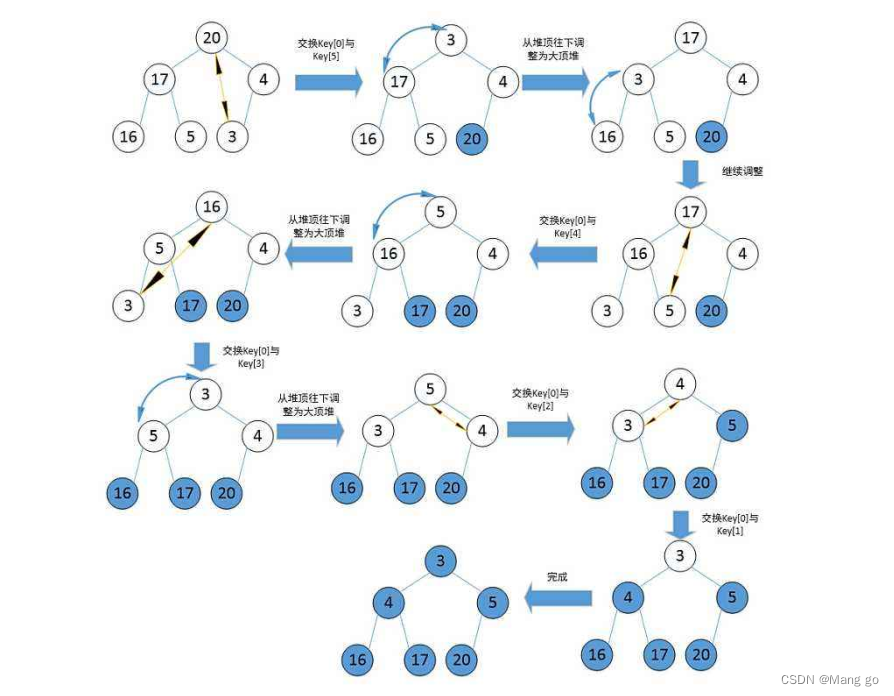
2.2.3 堆排序
堆排序(Heapsort)是指利用堆积树(堆)这种数据结构所设计的一种排序算法,它是选择排序的一种。它是通过堆来进行选择数据。需要注意的是排升序要建大堆,排降序建小堆。
代码实现:
public static void heapSort(int[] array){int end = array.length-1;createHeap(array);while(end > 0){swap(array,0,end);siftDown(array,0,end);end--;}}
public static void createHeap(int[] array){for (int i = (array.length-1-1)/2; i >= 0; i--) {siftDown(array,i,array.length);}}private static void siftDown(int[] array, int parent, int length) {int child = parent*2 + 1;while(child < length){if(child+1 < length && array[child] < array[child+1]){child++;}if(array[child] > array[parent]){swap(array,child,parent);parent = child;child = child*2 +1;}else{break;}}}【堆排序的特性总结】
- 堆排序使用堆来选数,效率就高了很多。
- 时间复杂度:O(N*logN)
- 空间复杂度:O(1)
- 稳定性:不稳定
2.3 交换排序
基本思想:所谓交换,就是根据序列中两个记录键值的比较结果来对换这两个记录在序列中的位置,交换排序的特
点是:将键值较大的记录向序列的尾部移动,键值较小的记录向序列的前部移动。
2.3.1冒泡排序
代码实现:
public static void bubbleSort(int[] array){for (int i = 0; i < array.length-1; i++) {boolean flg = false;for (int j = 0; j < array.length-1-i; j++) {if(array[j] > array[j+1]){swap(array,j,j+1);flg = true;}}if(!flg){break;}}}
【冒泡排序的特性总结】
- 冒泡排序是一种非常容易理解的排序
- 时间复杂度:O(N^2)
- 空间复杂度:O(1)
- 稳定性:稳定
2.3.2 快速排序
快速排序是Hoare于1962年提出的一种二叉树结构的交换排序方法,其基本思想为:任取待排序元素序列中的某元素作为基准值,按照该排序码将待排序集合分割成两子序列,左子序列中所有元素均小于基准值,右子序列中所有元素均大于基准值,然后最左右子序列重复该过程,直到所有元素都排列在相应位置上为止。
代码实现:
public static void quickSort(int[] array){quick(array,0,array.length-1);}public static void quick(int[] array,int start,int end){if(start >= end){return;}int mid= midIndex(array,start,end);swap(array,mid,start);int quickIndex = quickationHole(array,start,end);quick(array,start,quickIndex-1);quick(array,quickIndex+1,end);}public static int quickation(int[] array,int left ,int right){int tmp = left;while(left < right){while(left < right && array[right] >= array[tmp]){right--;}while(left< right && array[left] <= array[tmp]){left++;}swap(array,left, right);}swap(array,left,tmp);return left;}public static int quickationHole(int[] array,int left,int right){int tmp = array[left];while(left < right){while(left < right && array[right] >= tmp){right--;}array[left] = array[right];while(left < right && array[left] <= tmp){left++;}array[right] = array[left];}array[left] = tmp;return right;}public static int midIndex(int[] array,int start,int end){int mid = (start + end)>>>2;if(array[start] < array[end]){if(array[mid] > array[start]){return start;}else if (array[end] < array[mid]){return end;}else {return mid;}}else{if(array[mid] > array[start]){return end;}else if (array[end] < array[mid]){return start;}else {return mid;}}}
非递归实现:
public static void quickSortNor(int[] array){int start = 0;int end = array.length-1;Stack<Integer> stack = new Stack<>();int quickIndex = quickationHole(array,start,end);if(start+1 < quickIndex){stack.push(start);stack.push(quickIndex-1);}if(quickIndex+1 < end){stack.push(quickIndex+1);stack.push(end);}while(!stack.empty()){end = stack.pop();start = stack.pop();quickIndex = quickationHole(array,start,end);if(start+1 < quickIndex){stack.push(start);stack.push(quickIndex-1);}if(quickIndex+1 < end){stack.push(quickIndex+1);stack.push(end);}}}public static int quickationHole(int[] array,int left,int right){int tmp = array[left];while(left < right){while(left < right && array[right] >= tmp){right--;}array[left] = array[right];while(left < right && array[left] <= tmp){left++;}array[right] = array[left];}array[left] = tmp;return right;}
【快速排序总结】
-
快速排序整体的综合性能和使用场景都是比较好的,所以才敢叫快速排序
-
时间复杂度:O(N*logN)

-
空间复杂度:O(logN)
-
稳定性:不稳定
2.4 归并排序
2.4.1 基本思想
归并排序(MERGE-SORT)是建立在归并操作上的一种有效的排序算法,该算法是采用分治法(Divide andConquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。 归并排序核心步骤
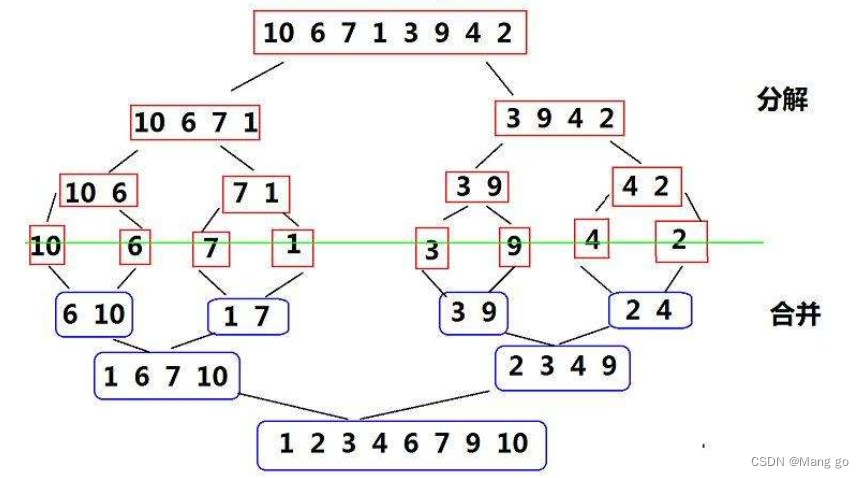
代码实现:
public static void mergeSort(int[] array){mergeSortFun(array,0,array.length-1);}private static void mergeSortFun(int[] array, int left, int right) {if(left >= right){return;}int mid = (left + right)/2;mergeSortFun(array,left,mid);mergeSortFun(array,mid+1,right);merge(array,left,mid,right);}private static void merge(int[] array,int left,int mid,int right){int s1 = left;int e1 = mid;int s2 = mid+1;int e2 = right;int[] tmparr = new int[right-left+1];int k =0;while(s1 <= e1 && s2 <= e2){if(array[s1] <= array[s2]){tmparr[k++] = array[s1++];}else{tmparr[k++] = array[s2++];}}while(s1 <= e1){tmparr[k++] = array[s1++];}while (s2 <= e2){tmparr[k++] = array[s2++];}for (int i = 0; i < tmparr.length; i++) {array[left+i] = tmparr[i];}}
非递归先实现:
public static void mergeSortNor(int[] array){int gap = 1;while(gap < array.length){for(int i = 0;i < array.length;i= i+gap*2){int left = i;int mid = left + gap -1;int right = mid + gap;if(mid >= array.length){mid = array.length-1;}if (right >= array.length) {right = array.length-1;}merge(array,left,mid,right);}gap*=2;}}private static void merge(int[] array,int left,int mid,int right){int s1 = left;int e1 = mid;int s2 = mid+1;int e2 = right;int[] tmparr = new int[right-left+1];int k =0;while(s1 <= e1 && s2 <= e2){if(array[s1] <= array[s2]){tmparr[k++] = array[s1++];}else{tmparr[k++] = array[s2++];}}while(s1 <= e1){tmparr[k++] = array[s1++];}while (s2 <= e2){tmparr[k++] = array[s2++];}for (int i = 0; i < tmparr.length; i++) {array[left+i] = tmparr[i];}}
【归并排序总结】
- 归并的缺点在于需要O(N)的空间复杂度,归并排序的思考更多的是解决在磁盘中的外排序问题。
- 时间复杂度:O(N*logN)
- 空间复杂度:O(N)
- 稳定性:稳定
2.4.2 海量数据的排序问题
外部排序:排序过程需要在磁盘等外部存储进行的排序
前提:内存只有 1G,需要排序的数据有 100G
因为内存中因为无法把所有数据全部放下,所以需要外部排序,而归并排序是最常用的外部排序
- 先把文件切分成 200 份,每个 512 M
- 分别对 512 M 排序,因为内存已经可以放的下,所以任意排序方式都可以
- 进行 2路归并,同时对 200 份有序文件做归并过程,最终结果就有序了
3. 排序算法复杂度及稳定性分析
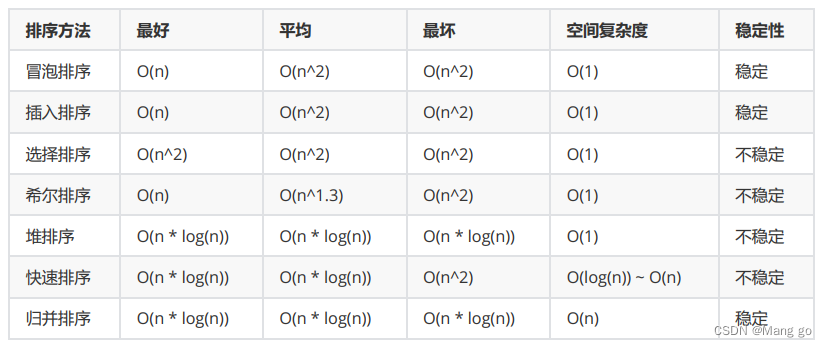
相关文章:

排序【七大排序】
文章目录 1. 排序的概念及引用1.1 排序的概念1.2 常见的排序算法 2. 常见排序算法的实现2.1 插入排序2.1.1基本思想:2.1.2 直接插入排序2.1.3 希尔排序( 缩小增量排序 ) 2.2 选择排序2.2.1基本思想:2.2.2 直接选择排序:2.2.3 堆排序 2.3 交换排序2.3.1冒…...

人大与加拿大女王大学金融硕士项目——立即行动,才是缓解焦虑的解药
!在这个经济飞速的发展的时代,我国焦虑症的患病率为7%,焦虑已经超越个体范畴,成为整个社会与时代的课题。焦虑,往往源于我们想要达到的,与自己拥有的所产生的差距。任何事情,开始做远比准备做更会给人带来成…...
)
老卫带你学---leetcode刷题(46. 全排列)
46. 全排列 问题: 给定一个不含重复数字的数组 nums ,返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。 示例 1:输入:nums [1,2,3] 输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]示例 2&#x…...

6.6 图的应用
思维导图: 6.6.1 最小生成树 ### 6.6 图的应用 #### 主旨:图的概念可应用于现实生活中的许多问题,如网络构建、路径查询、任务排序等。 --- #### 6.6.1 最小生成树 **概念**:要在n个城市中建立通信联络网,则最少需…...

100问GPT4与大语言模型的关系以及LLMs的重要性
你现在是一个AI专家,语言学家和教师,你目标是让我理解语言模型的概念,理解ChatGPT 跟语言模型之间的关系。你的工作是以一种易于理解的方式解释这些概念。这可能包括提供 例子,提出问题或将复杂的想法分解成更容易理解的小块。现在…...
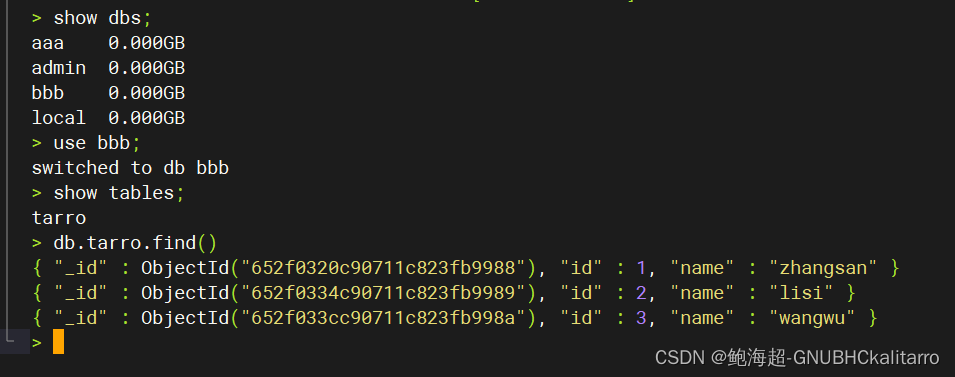
Linux:mongodb数据逻辑备份与恢复(3.4.5版本)
我在数据库aaa的里创建了一个名为tarro的集合,其中有三条数据 备份语法 mongodump –h server_ip –d database_name –o dbdirectory 恢复语法 mongorestore -d database_name --dirdbdirectory 备份 现在我要将aaa.tarro进行备份 mongodump --host 192.168.254…...
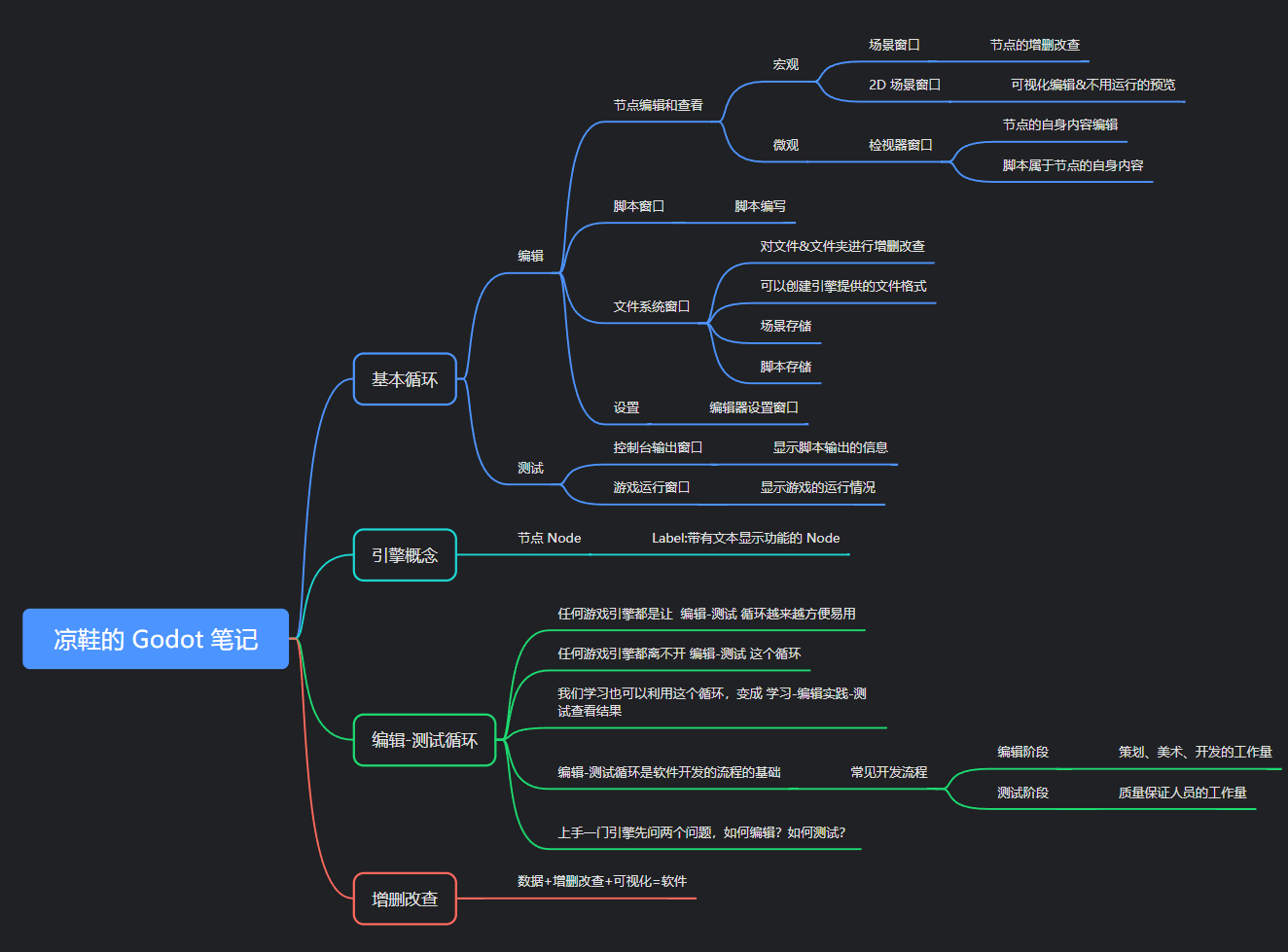
凉鞋的 Godot 笔记 109. 专题一 小结
109. 专题一 小结 在这一篇,我们来对第一个专题做一个小的总结。 到目前为止,大家应该能够感受到此教程的基调。 内容的难度非常简单,接近于零基础的程度,不过通过这些零基础内容所介绍的通识内容其实是笔者好多年的时间一点点…...
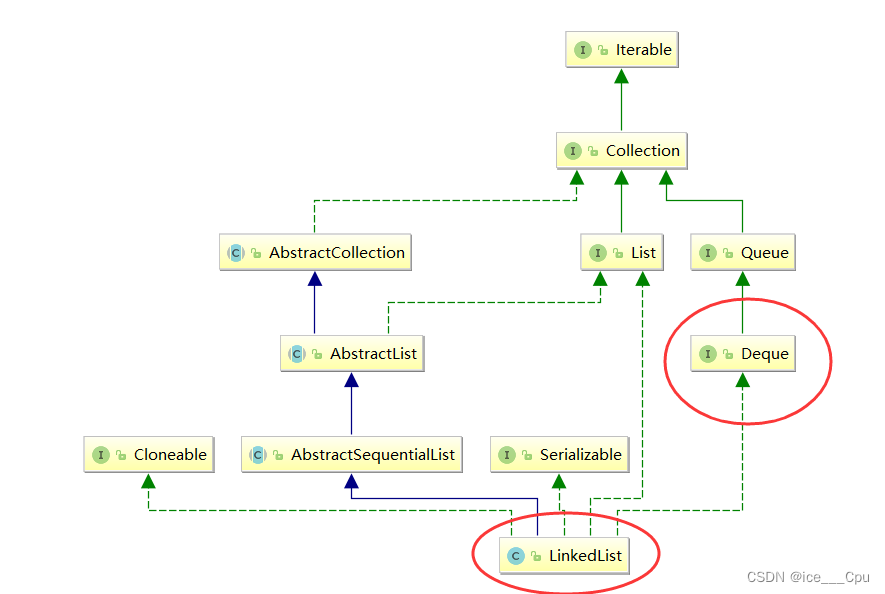
数据结构 - 4(栈和队列6000字详解)
一:栈 1.1 栈的概念 栈:一种特殊的线性表,其只允许在固定的一端进行插入和删除元素操作。进行数据插入和删除操作的一端称为栈顶,另一端称为栈底。栈中的数据元素遵守后进先出LIFO(Last In First Out)的原…...
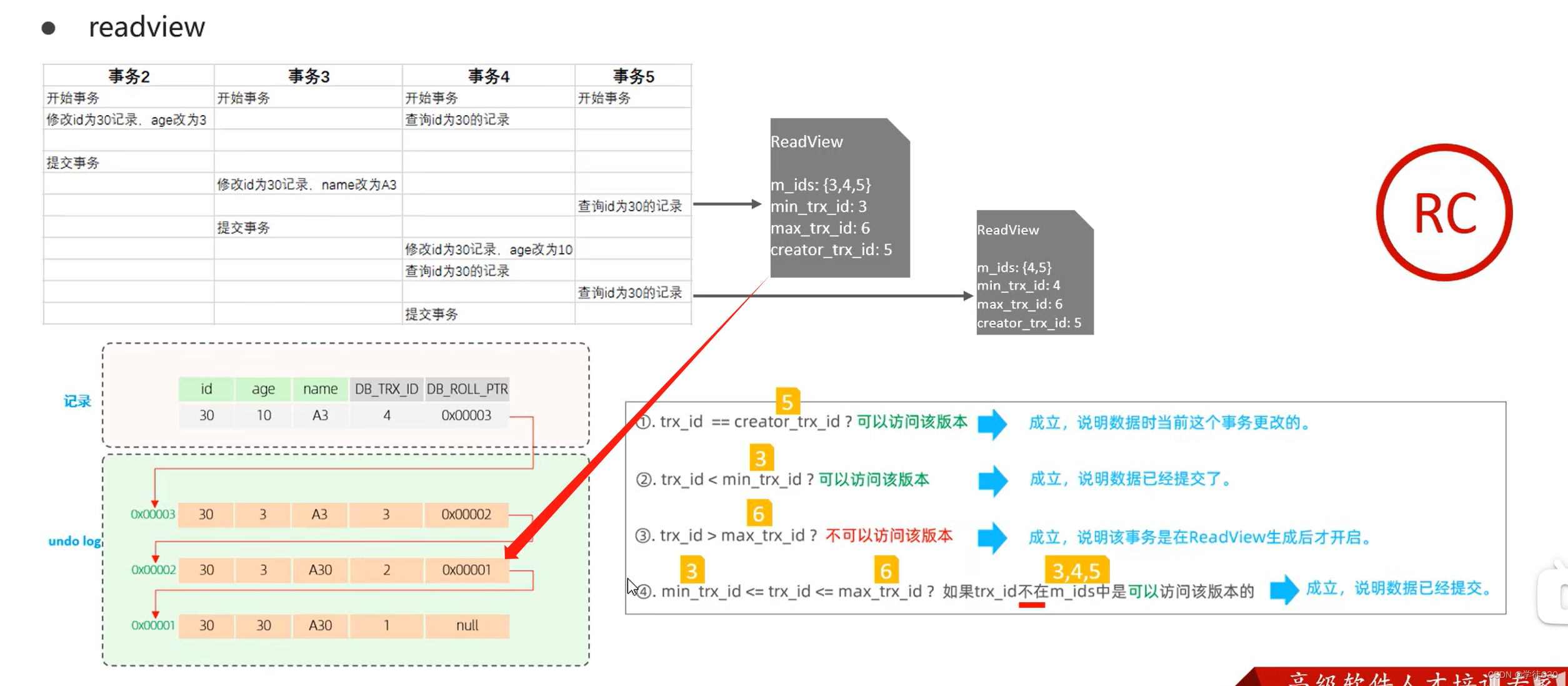
MySQL InnoDB引擎深入学习的一天(InnoDB架构 + 事务底层原理 + MVCC)
目录 逻辑存储引擎 架构 概述 内存架构 Buffer Pool Change Buffe Adaptive Hash Index Log Buffer 磁盘结构 System Tablespace File-Per-Table Tablespaces General Tablespaces Undo Tablespaces Temporary Tablespaces Doublewrite Buffer Files Redo Log 后台线程 事务原…...
TX Text Control .NET Server for ASP.NET 32.0 Crack
TX Text Control .NET Server for ASP.NET 是VISUAL STUDIO 2022、ASP.NET CORE .NET 6 和 .NET 7 支持,将文档处理集成到 Web 应用程序中,为您的 ASP.NET Core、ASP.NET 和 Angular 应用程序添加强大的文档处理功能。 客户端用户界面 文档编辑器 将功能…...
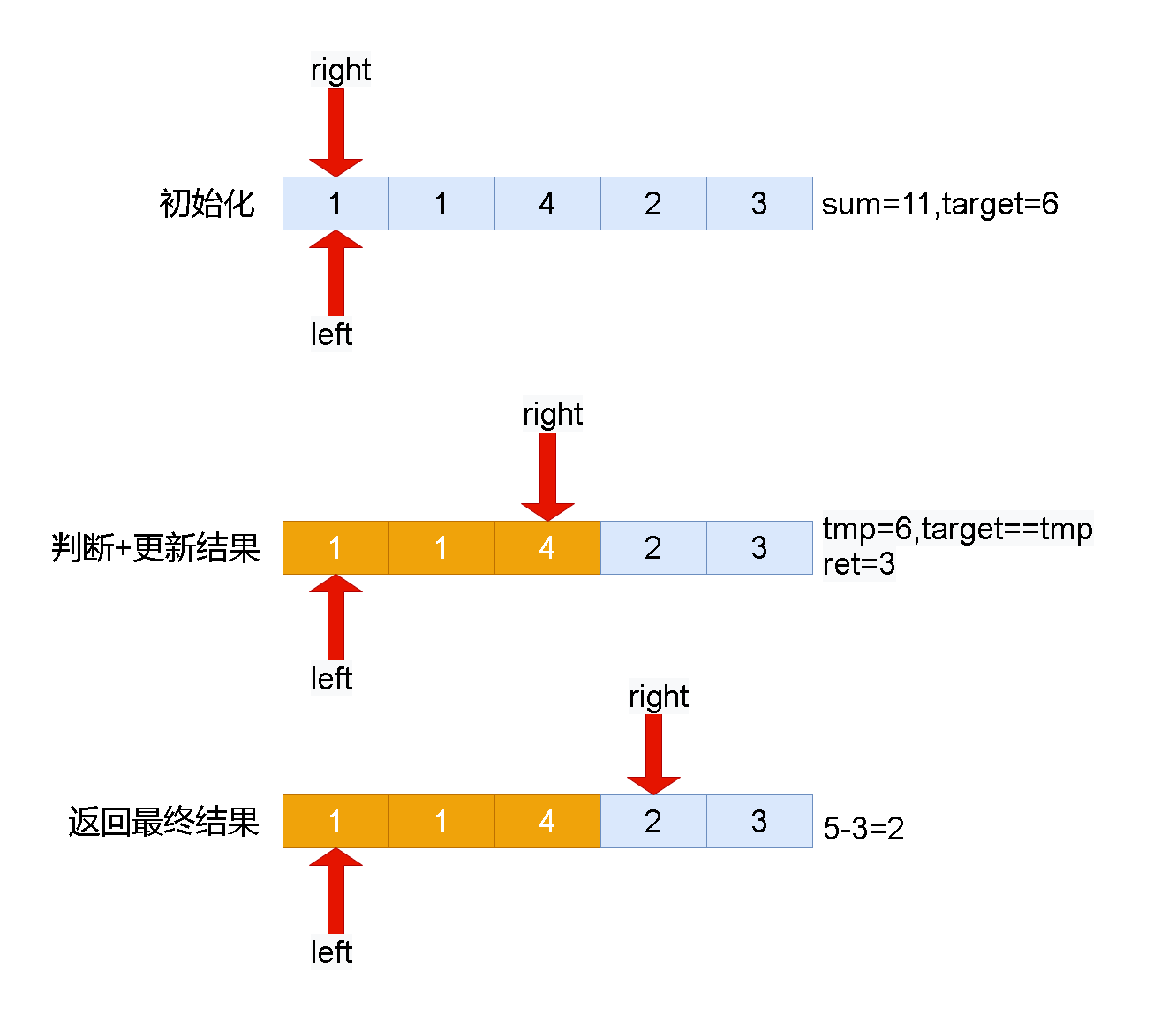
Leetcode刷题详解——将x减到0的最小操作数
1. 题目链接:1658. 将 x 减到 0 的最小操作数 2. 题目描述: 给你一个整数数组 nums 和一个整数 x 。每一次操作时,你应当移除数组 nums 最左边或最右边的元素,然后从 x 中减去该元素的值。请注意,需要 修改 数组以供接下来的操作…...

精选免费热门api接口分享
IP归属地-IPv4城市级:根据IP地址查询归属地信息,支持到城市级,包含国家、省、市、和运营商等信息。IP归属地-IPv6城市级:根据IP地址(IPv6版本)查询归属地信息,支持到中国大陆地区(不…...
androidx.appcompat.widget.Toolbar最右边设置控件不能仅靠最右边
androidx.appcompat.widget.Toolbar最右边设置控件不能仅靠最右边 Android Toolbar左、中、右对齐-CSDN博客Android Toolbar左、中、右对齐默认的Android Toolbar中添加子元素view是从左到右依次添加。需要注意的是,Android Toolbar为自身的…...
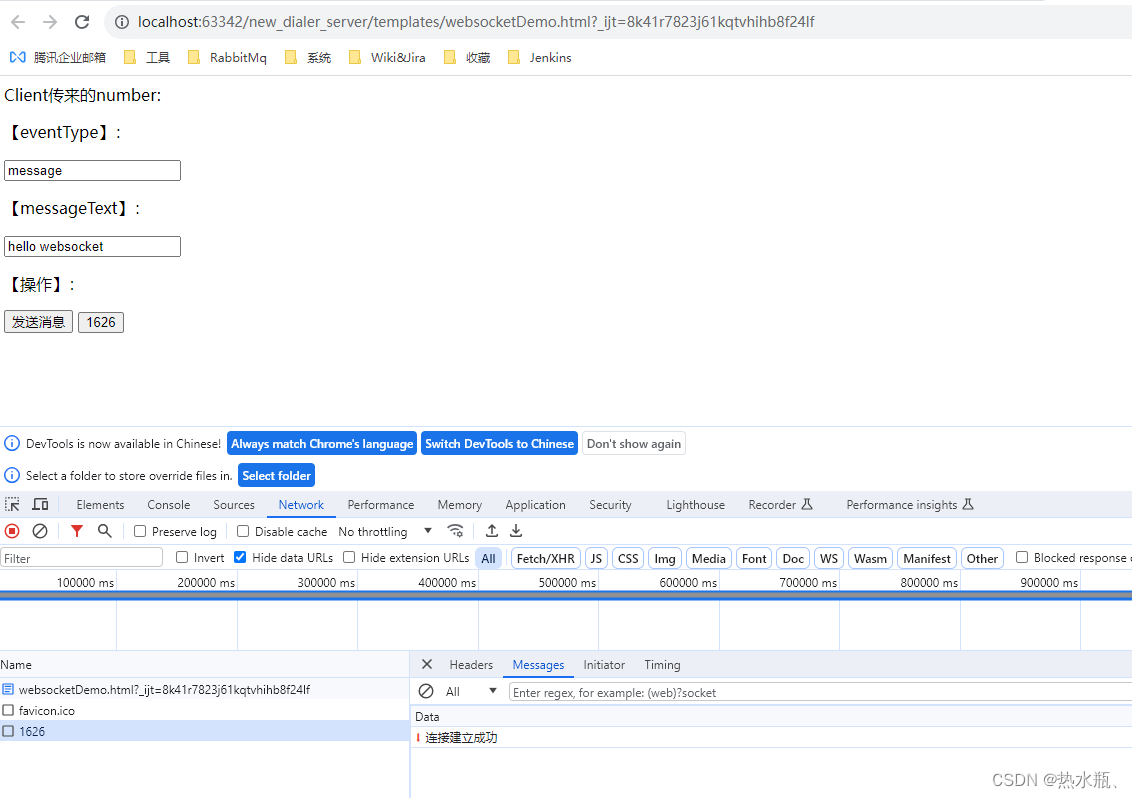
Springboot整合WebSocket实现浏览器和服务器交互
Websocket定义 代码实现 引入maven依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-websocket</artifactId></dependency>配置类 import org.springframework.context.annotation.Bean;i…...

这些 channel 用法你都用起来了吗?
channel 是什么? channel 是GO语言中一种特殊的类型,是连接并发goroutine的管道 channel 通道是可以让一个 goroutine 协程发送特定值到另一个 goroutine 协程的通信机制。 关于 channel 的原理,channel通道需要注意的地方,之前…...

纽交所上市公司安费诺宣布将以1.397亿美元收购无线解决方案提供商PCTEL
来源:猛兽财经 作者:猛兽财经 猛兽财经获悉,纽交所上市公司安费诺(APH)宣布将以每股7美元现金,总价格1.397亿美元收购无线解决方案提供商PCTEL(PCTI)。 该交易预计将在第四季度或2024年初完成。 Lake Street Capital Markets担任…...
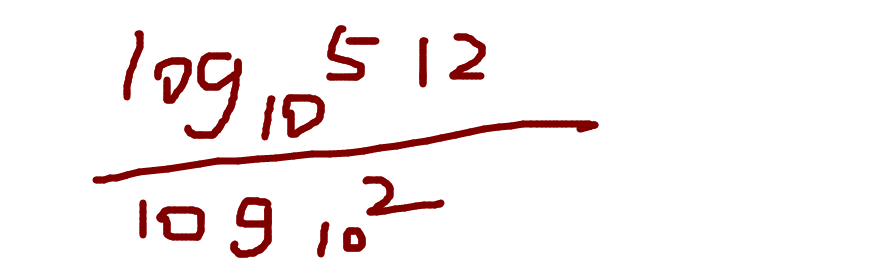
二分查找算法(Python)
目录 1、概念 2、思路 3、实现算法 1、概念 二分查找又称折半查找,它是一种效率较高的查找方法 原理:首先,假设表中元素是按升序排列,将表中间位置记录的关键字与查找关键字比较,如果两者相等,则查找成…...

“第四十二天”
这个,之前用的b去存储a的总和和排名,后来在比较的过程中,只改变的b的值,却没有改变a的值,但在比较语文成绩的时候用的还是a,这个时候a和b同样是第i个对应的可能不是同一个对象了 ,因为上面b的值…...

Qt/C++编写物联网组件/支持modbus/rtu/tcp/udp/websocket/mqtt/多线程采集
一、功能特点 支持多种协议,包括Modbus_Rtu_Com/Modbus_Rtu_Tcp/Modbus_Rtu_Udp/Modbus_Rtu_Web/Modbus_Tcp/Modbus_Udp/Modbus_Web等,其中web指websocket。支持多种采集通讯方式,包括串口和网络等,可自由拓展其他方式。自定义采…...
windows常用命令
一.文件操作 dir:查看文件当前路径目录列表 cd .. :返回上一级目录 cd 路径:进入路径...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...

基于大模型的 UI 自动化系统
基于大模型的 UI 自动化系统 下面是一个完整的 Python 系统,利用大模型实现智能 UI 自动化,结合计算机视觉和自然语言处理技术,实现"看屏操作"的能力。 系统架构设计 #mermaid-svg-2gn2GRvh5WCP2ktF {font-family:"trebuchet ms",verdana,arial,sans-…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...

Yolov8 目标检测蒸馏学习记录
yolov8系列模型蒸馏基本流程,代码下载:这里本人提交了一个demo:djdll/Yolov8_Distillation: Yolov8轻量化_蒸馏代码实现 在轻量化模型设计中,**知识蒸馏(Knowledge Distillation)**被广泛应用,作为提升模型…...

安宝特案例丨Vuzix AR智能眼镜集成专业软件,助力卢森堡医院药房转型,赢得辉瑞创新奖
在Vuzix M400 AR智能眼镜的助力下,卢森堡罗伯特舒曼医院(the Robert Schuman Hospitals, HRS)凭借在无菌制剂生产流程中引入增强现实技术(AR)创新项目,荣获了2024年6月7日由卢森堡医院药剂师协会࿰…...

Go 语言并发编程基础:无缓冲与有缓冲通道
在上一章节中,我们了解了 Channel 的基本用法。本章将重点分析 Go 中通道的两种类型 —— 无缓冲通道与有缓冲通道,它们在并发编程中各具特点和应用场景。 一、通道的基本分类 类型定义形式特点无缓冲通道make(chan T)发送和接收都必须准备好࿰…...

基于SpringBoot在线拍卖系统的设计和实现
摘 要 随着社会的发展,社会的各行各业都在利用信息化时代的优势。计算机的优势和普及使得各种信息系统的开发成为必需。 在线拍卖系统,主要的模块包括管理员;首页、个人中心、用户管理、商品类型管理、拍卖商品管理、历史竞拍管理、竞拍订单…...

android RelativeLayout布局
<?xml version"1.0" encoding"utf-8"?> <RelativeLayout xmlns:android"http://schemas.android.com/apk/res/android"android:layout_width"match_parent"android:layout_height"match_parent"android:gravity&…...

Python网页自动化Selenium中文文档
1. 安装 1.1. 安装 Selenium Python bindings 提供了一个简单的API,让你使用Selenium WebDriver来编写功能/校验测试。 通过Selenium Python的API,你可以非常直观的使用Selenium WebDriver的所有功能。 Selenium Python bindings 使用非常简洁方便的A…...
