数据结构----算法--五大基本算法
数据结构----算法–五大基本算法
一.贪心算法
1.什么是贪心算法
在有多个选择的时候不考虑长远的情况,只考虑眼前的这一步,在眼前这一步选择当前的最好的方案
二.分治法
1.分治的概念
分治法:分而治之
将一个问题拆解成若干个解决方式完全相同的问题
满足分治的四个条件
1.问题难度随着数据规模缩小而降低
2.问题可拆分
3.子问题间相互独立
4.子问题的解可合并
2.典型的分治:二分查找(折半搜索) BinaryChop
前提:有序
时间复杂度O(log2的n次方)
1.循环实现二分查找
//循环
int BinaryChop1(int a[], int begin, int end ,int find) {if (a == nullptr || begin > end) return -1;while (begin<= end) {int mid = begin+(end- begin)/2 ;if (a[mid] == find) {cout << "找到了,返回在数组中的下标" << endl;return mid;}else if (a[mid] < find) {begin = mid + 1;}else if (a[mid] > find) {end = mid - 1;}}return -1;
}
2.递归实现二分查找
//递归
int BinaryChop2(int a[], int begin, int end, int find) {if (a == nullptr || begin > end) return -1;int mid = begin+(end- begin)/2;if (a[mid] == find) {cout << "找到了,返回数组下标" << endl;return mid;}else if (a[mid] < find) {begin = mid + 1;}else if (a[mid] > find) {end = mid - 1;}return BinaryChop2(a, begin, end, find);}
三.回溯法
1.回溯法解决的问题
1.求子集的问题
2.求排列的问题
3.求集合的问题
4.求棋盘的问题
2.回溯常见的写法
循环嵌套递归
3.用回溯法解决一道全排列的问题(此题的网址为https://leetcode.cn/problems/permutations/)
此题在之前的博客中具体分析过(博客的网址如下https://blog.csdn.net/m0_73483024/article/details/133589061?spm=1001.2014.3001.5502)
题目:
四.动态规划(Dynamic Programming)
1.动态规划可以解决的问题
动态规划可以用来求最优解(最大、最小、最多等)的问题
2.动态规划操作对象所要满足的性质
大问题可以拆解成解决方案完全相同的子问题,并且要满足以下两个性质
1.满足最优子结构性质(子问题的最优解构成当前问题的最优解)
2.无后效性(一旦某一状态被确定,那么过去这个状态如何求得的我们就再也不关注了)
3.动态规划的求解过程
1.拆分
2.定状态(子问题的最优解)
3.做决策
4.求状态转移方程
4.动态规划的实现手段
1.自顶向下带备忘的解法(大到小)
2.自底向上的解法(小到大)
注意:动态规划的空间消耗是用来换时间了
5.关于动态规划的问题
1.凑钱问题
题目:
有1元,3元,5元面额的钞票,想要凑到n元钱
解决方法:
创建一个f数组
f(n)表示想要凑到n元钱所需要的最小的钞票数
我们观察下面式子,找出规律
f(0)=0
f(1)=f(1-1)+1=1
f(2)=f(2-1)+1=2
f(3)=min{f(3-3)+1=1,f(3-1)+1=3}=1
f(4)=min{f(4-3)+1=2,f(4-1)+1=2}=2
f(5)=min{f(5-5)+1=1,f(5-3)+1=3,f(5-1)+1=3}=1
推导出动态转移方程得
f(i)=min{f(i-v[j])}+1(v[j]<=i)
这里v是一个存1元,3元,5元面额的钞票的数组,j是遍历v数组的变量
2.一维的动态划分问题:最长递增子序列(LIS)
题目:
有一个数组中有6、3、9、8、4、7、2、5、10、1这些元素,找到这个数组中的最长递增子序列
解决方法:
方法一
创建一个f数组
f(n)表示n下标与前序元素构成的LIS的长度
我们观察下面式子,找出规律
f(0)=1
f(1)=1
f(2)=max{9>3 f(1)+1=2
9>6 f(0)+1=2
1(只有自己本身,长度为1)
}=2
f(3)=max{8>3 f(1)+1=2
8>6 f(0)+1=2
1(只有自己本身,长度为1)
}=2
f(4)=max{4>3 f(1)+1=2
1(只有自己本身,长度为1)
}=2
f(5)=max{7>4 f(4)+1=3
7>3 f(1)+1=2
7>6 f(0)+1=2
1(只有自己本身,长度为1)
}=3
推导出动态转移方程得
f(i)=max(f(j)+1,1) (v[j]<v[i],0<=j<i)
这里v是数组,i和j是遍历v数组的变量
方法二(相较于方法一优化)
创建一个数组用来存等长LIS右边界的最小值(下标当作长度)
从左到右遍历数组,对创建的数组进行更新,最后数组的使用量就是最长递增子序列的长度
看下面进行理解
f(0)=1
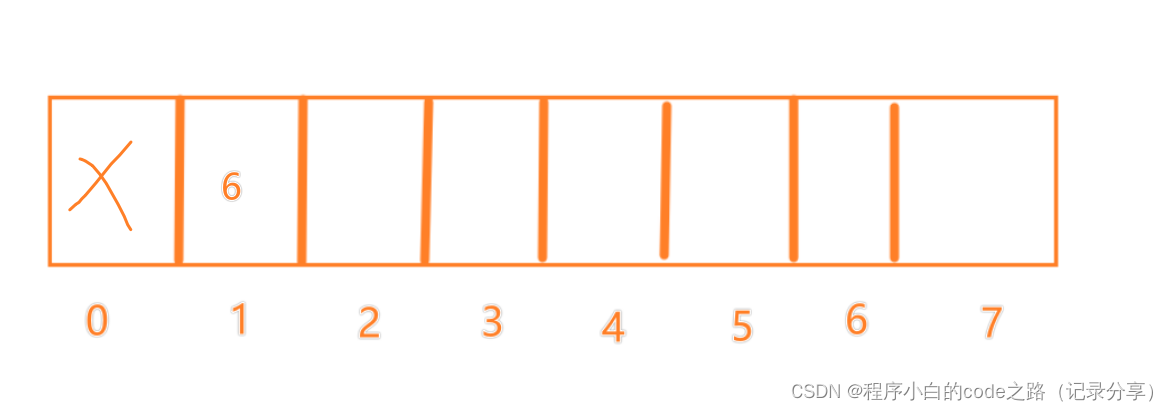
f(1)=1
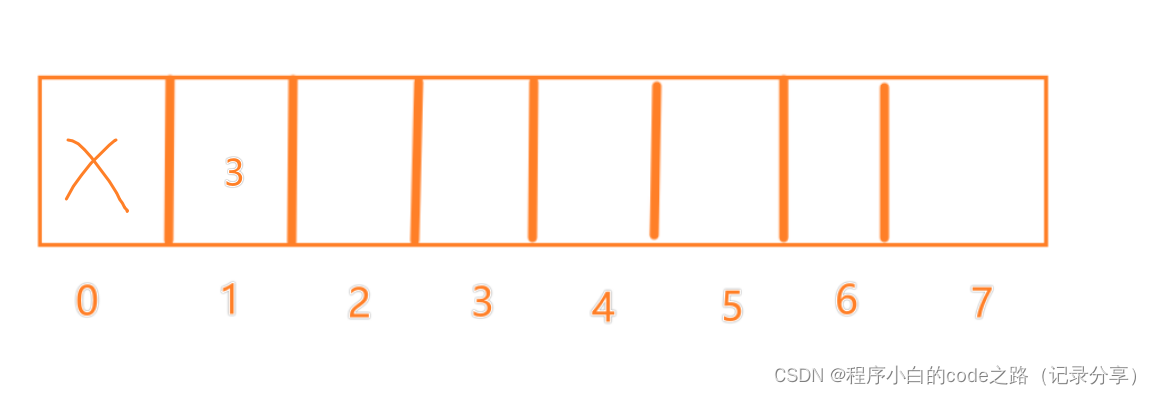
f(2)=2
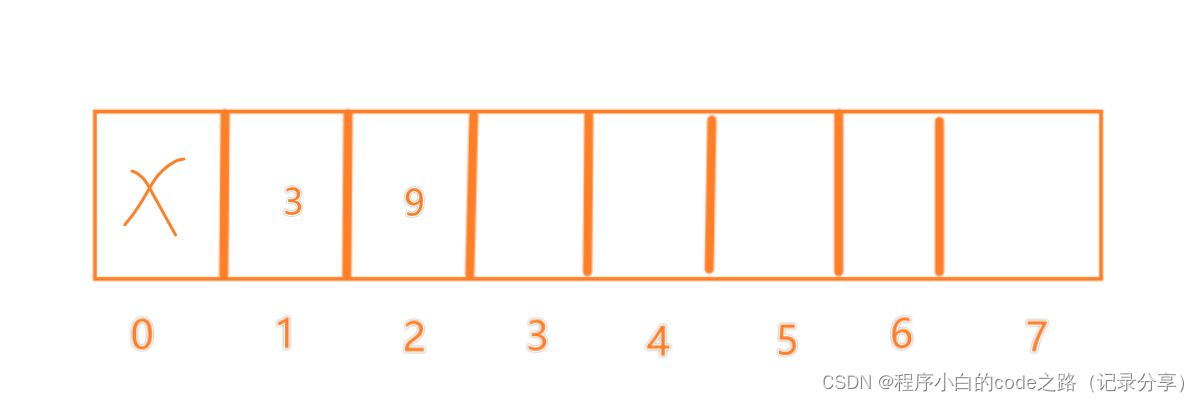
f(3)=2
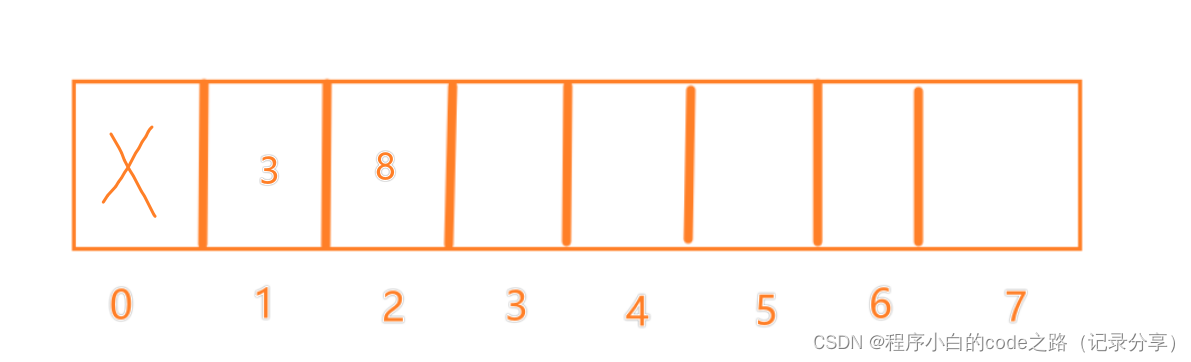
f(4)=2
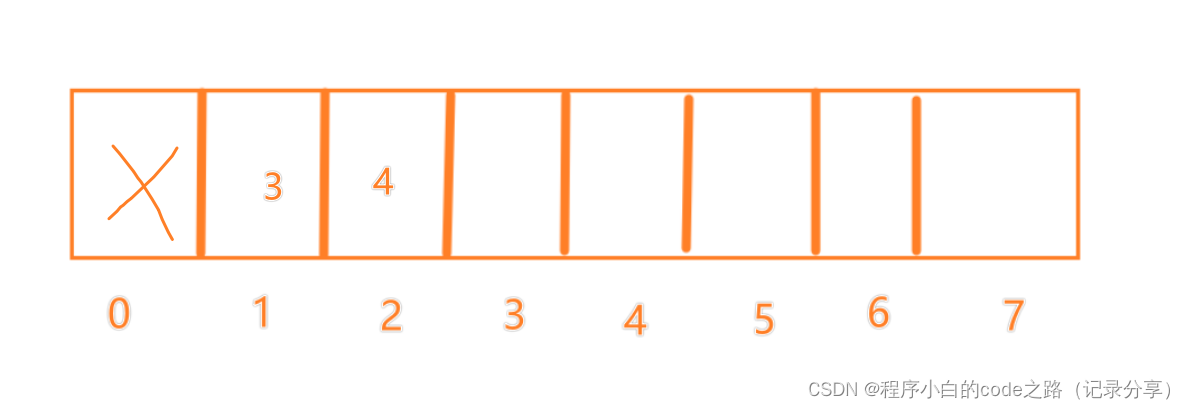
f(5)=3
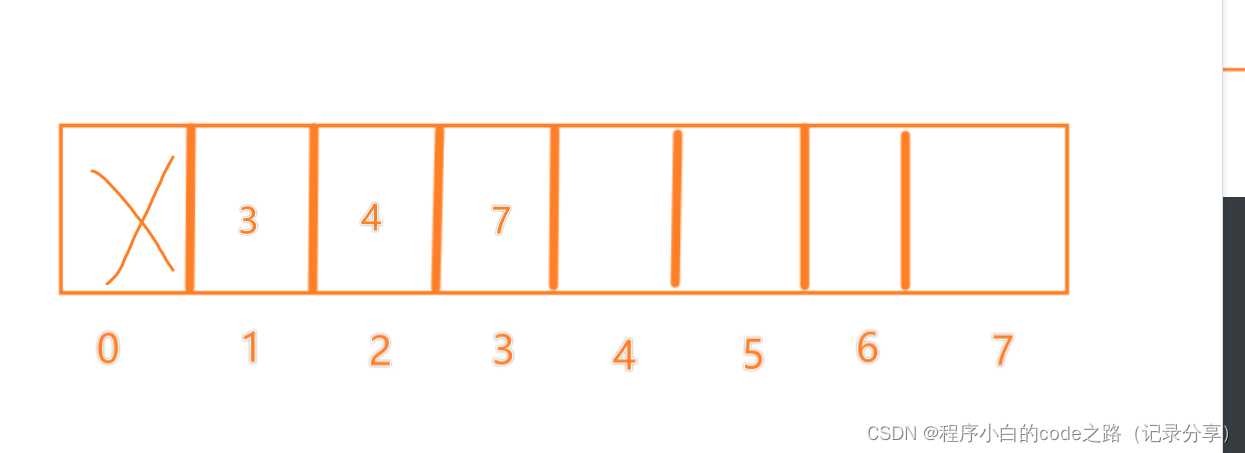
下面的过程就不再写了
方法三(在方法二的基础上,进行二分搜索,在进行数组的更新时使用二分搜索)
3.二维的动态规划问题:捡苹果
题目:
有一个m*n的格子,每个格子中有数量不一的苹果,一个小机器人(只能往右或者往下走)从左上角走到它不能再走了,求它最多能捡到多少个苹果
解决:
状态转移方程为 c[i] [j]=max{c[i-1] [j],c[i] [j-1]}+A[i] [j]
c数组存的是到每个位置所能捡到的最大苹果数量,A数组存的是每个位置的苹果数量
4.二维的动态规划问题且带附加条件的:最长公共子序列(LCS)
题目:
求X数组{A,B,B,D,C,B,C}与Y数组{B,C,D,B,A,C}的最长公共子序列
解决:
状态转移方程为 c[i] [j]={c[i-1] [j-1]+1 xi==yi
max{c[i-1] [j],c[i] [j-1]}} xi!=yi
}
c数组存的是x数组走到数组中的某个元素和y数组走到数组中的某个元素时,二者所构成的LCS的长度
c[i] [j]存的是x数组走到第i个元素,y数组走到第j个元素,二者所构成的LCS的长度
四.博弈树
1.博弈树(Game Tree)
棋类中用到的博弈树满足的条件
1.二者零和
2.全信息
3.非偶然
注意:博弈树要在时间消耗和结果准确度中做一个平衡
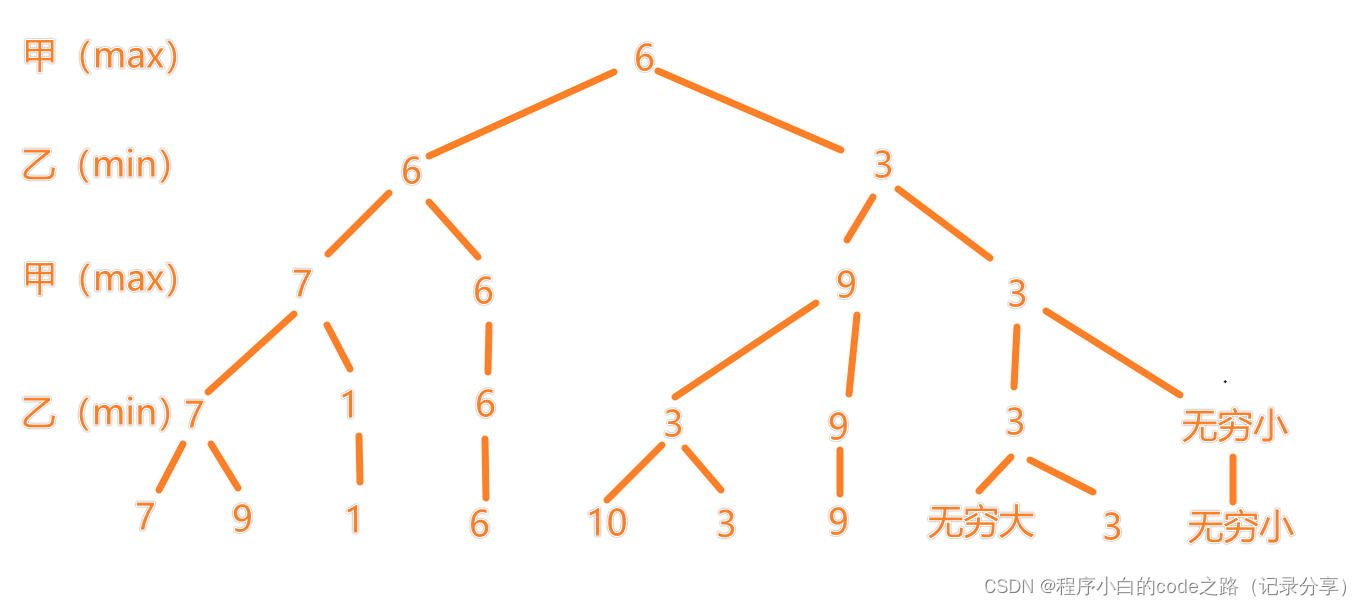
2.极大极小搜索树(是在原有博弈树的基础上实现的)
看下面这张图理解博弈树
甲是自己要选择尽量大的
乙是对手要使我们最小,所以乙选择尽量小的
3.α-β剪枝(对极大极小树的优化)
看下面图片(都是部分图,不是完整的)理解α-β剪枝
图片一
注意:这是一个深搜过程(图中数字表示处理的步骤)
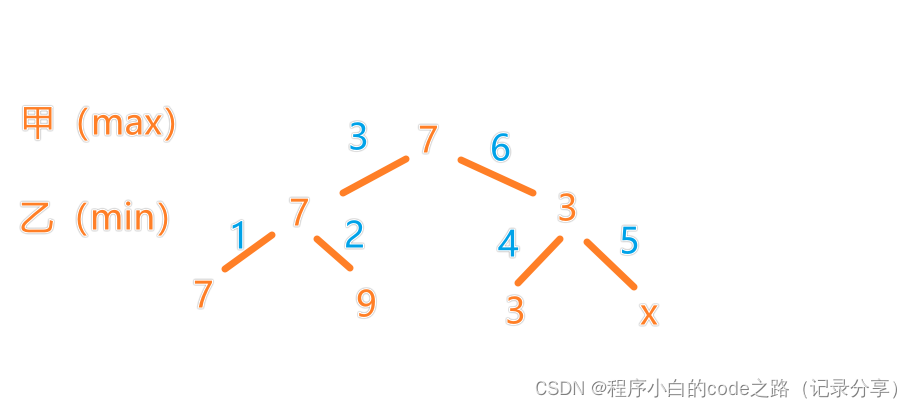
当此图第4步得到的值小于第3步得到的值,那么第5步就不用处理了
图片二
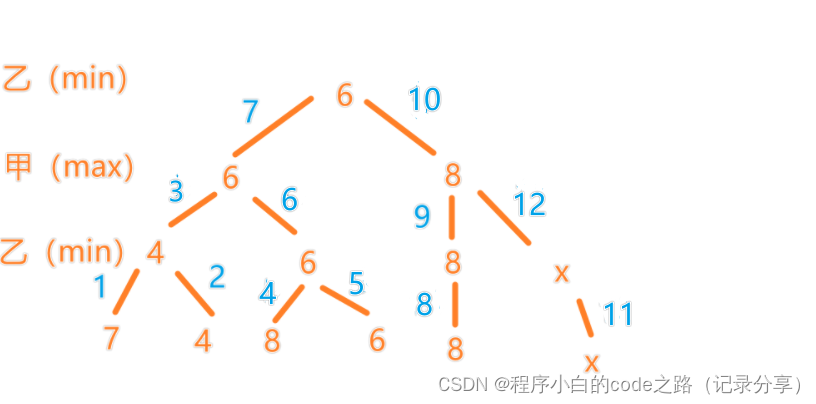
注意:这是一个深搜过程(图中数字表示处理的步骤)
当此图第9步得到的值大于第7步得到的值,那么第11步和第12步就不用处理了
五.银行家算法
1.使用银行家算法要满足的条件
1.固定数量的进程共享固定数量的资源
2.进程最大请求资源数
3.单次申请的资源数不能超出可分配资源数
4.不是一次性全部申请,分批次进行
5.进程等待资源的时间是有限的(不会无休止等待)
6.当满足进程的最大资源需求,进程应该在有限时间内归还资源
2.银行家算法的操作步骤
A:总资产
B:所需的最大资源数
C:已经分配的资源数
D:仍然需要的资源数
E:每次请求的资源数
F:可分配的资源数
1.看E<=F是否满足
如果不满足就等待
如果满足就进行下一步
2.看E<=D是否满足
如果不满足,失败
如果满足就进行下一步
3.假装分配,更新各个值
C=C+E
D=D-E
F=F-E
相关文章:

数据结构----算法--五大基本算法
数据结构----算法–五大基本算法 一.贪心算法 1.什么是贪心算法 在有多个选择的时候不考虑长远的情况,只考虑眼前的这一步,在眼前这一步选择当前的最好的方案 二.分治法 1.分治的概念 分治法:分而治之 将一个问题拆解成若干个解决方式…...

网格大师如何把b3dm转为osgb格式?
答:在网格大师的倾斜数据处理工具中选中“3DTiles转OSGB”,设定数据输入路径和输出路径提交任务即可。 网格大师是一款能够解决实景三维模型空间参考、原点、瓦块大小不统一,重叠区域处理问题的工具“百宝箱”,集格式转换、坐标转…...
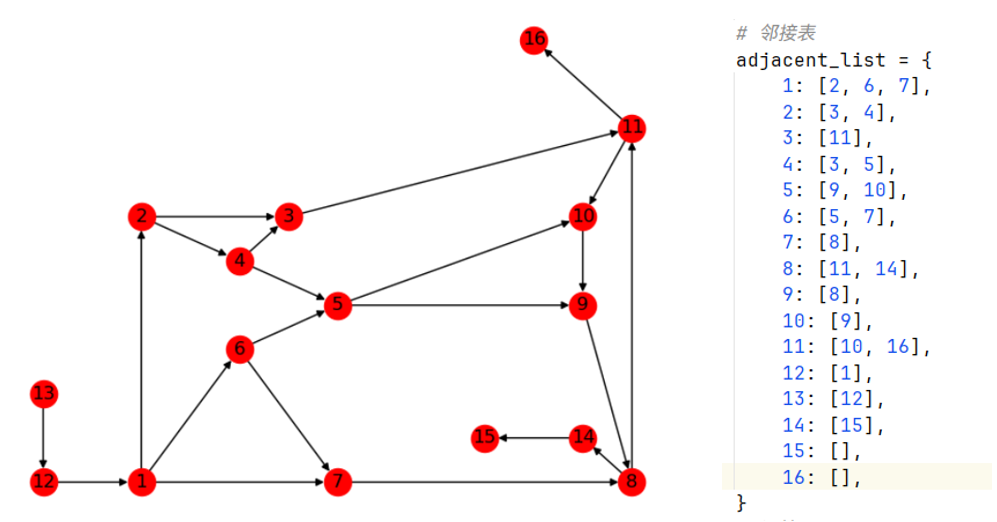
基于深度优先搜索的图遍历
这里写目录标题 基于深度优先搜索的无向图遍历算法流程图Python实现Java实现 基于深度优先搜索的有向图遍历Python实现 基于深度优先搜索的无向图遍历 使用深度优先搜索遍历无向图,将无向图用邻接表存储: 算法流程图 初始化起点 source,当…...

Web3D虚拟人制作简明指南
如何在线创建虚拟人? 虚拟人,也称为数字化身、虚拟助理或虚拟代理,是一种可以通过各种在线平台与用户进行逼真交互的人工智能人。 在线创建虚拟人变得越来越流行,因为它为个人和企业带来了许多好处。 通过虚拟助理或代理,您可以以更具吸引力和个性化的方式与客户或受众进…...
:基本概念、创建表)
【大数据 - Doris 实践】数据表的基本使用(一):基本概念、创建表
数据表的基本使用(一):基本概念、创建表 1.创建用户和数据库2.Doris 中数据表的基本概念2.1 Row & Column2.2 Partition & Tablet 3.建表实操3.1 建表语法3.2 字段类型3.3 创建表3.3.1 Range Partition3.3.2 List Partition 1.创建用…...
剑指Offer || 038.每日温度
题目 请根据每日 气温 列表 temperatures ,重新生成一个列表,要求其对应位置的输出为:要想观测到更高的气温,至少需要等待的天数。如果气温在这之后都不会升高,请在该位置用 0 来代替。 示例 1: 输入: temperatures…...
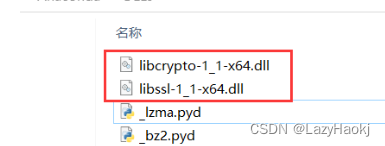
URL because the SSL module is not available
Could not fetch URL https://pypi.org/simple/pip/: There was a problem confirming the ssl certificate: HTTPSConnectionPool(host‘pypi.org’, port443): Max retries exceeded with url: /simple/pip/ (Caused by SSLError(“Can’t connect to HTT PS URL because the…...
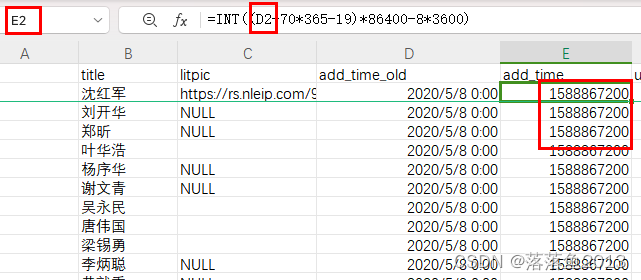
excel 日期与时间戳的相互转换
1、日期转时间戳:B1INT((A1-70*365-19)*86400-8*3600)*1000 2、时间戳转日期:A1TEXT((B1/10008*3600)/8640070*36519,"yyyy-mm-dd hh:mm:ss") 以上为精确到毫秒,只精确到秒不需要乘或除1000。 使用以上方法可以进行excel中日期…...

MongoDB中的嵌套List操作
前言 MongoDB区别Mysql的地方,就是MongoDB支持文档嵌套,比如最近业务中就有一个在音频转写结果中进行对话场景,一个音频中对应多轮对话,这些音频数据和对话信息就存储在MongoDB中文档中。集合结构大致如下 {"_id":234…...
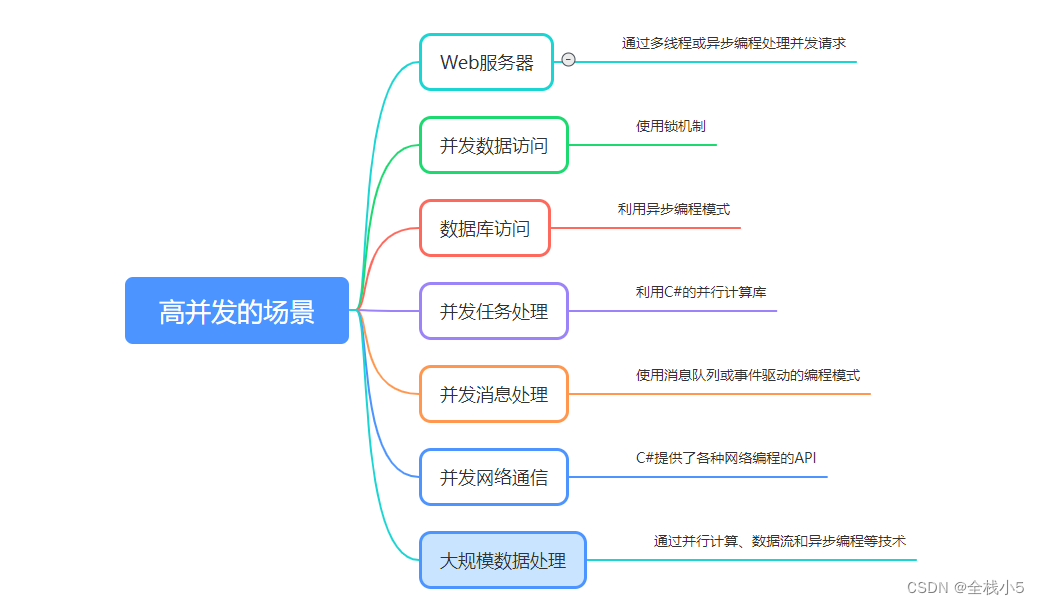
【C#】什么是并发,C#常规解决高并发的基本方法
给自己一个目标,然后坚持一段时间,总会有收获和感悟! 在实际项目开发中,多少都会遇到高并发的情况,有可能是网络问题,连续点击鼠标无反应快速发起了N多次调用接口, 导致极短时间内重复调用了多次…...
MySQL双主一从高可用
MySQL双主一从高可用 文章目录 MySQL双主一从高可用环境说明1.配置前的准备工作2.配置yum源 1.在部署NFS服务2.安装主数据库的数据库服务,并挂载nfs3.初始化数据库4.配置两台master主机数据库5.配置m1和m2成为主数据库6.安装、配置keepalived7.安装部署从数据库8.测…...

#力扣:2894. 分类求和并作差@FDDLC
2894. 分类求和并作差 - 力扣(LeetCode) 一、Java class Solution {public int differenceOfSums(int n, int m) {return (1n)*n/2-n/m*(mn/m*m)/2;} } 二、C class Solution { public:int differenceOfSums(int n, int m) {return (1n)*n/2-n/m*(mn…...
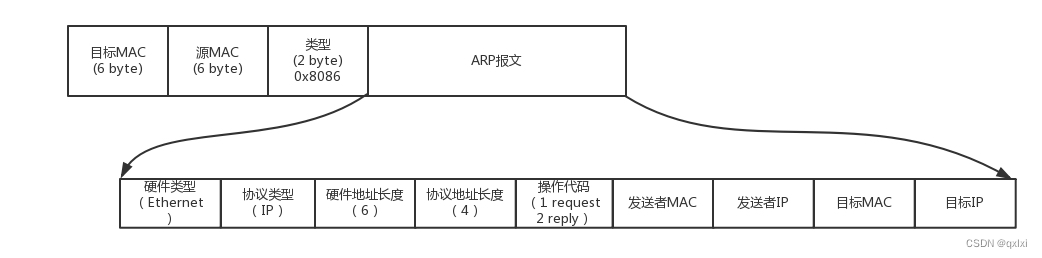
【网络协议】聊聊从物理层到MAC层 ARP 交换机
物理层 物理层其实就是电脑、交换器、路由器、光纤等。组成一个局域网的方式可以使用集线器。可以将多台电脑连接起来,然后进行将数据转发给别的端口。 数据链路层 Hub其实就是广播模式,如果A电脑发出一个包,B、C电脑也可以收到。那么数据…...
WordPress插件 WP-PostViews 汉化语言包
WP-PostViews汉化语言包 WP-PostViews是一款很受欢迎的文章浏览次数统计插件,记录每篇文章展示次数、根据展示次数显示历史最热或最衰的文章排行、展示范围可以是全部文章和页面,也可以是某些目录下的文章和页面。本文还介绍了一些隐藏的功能࿰…...
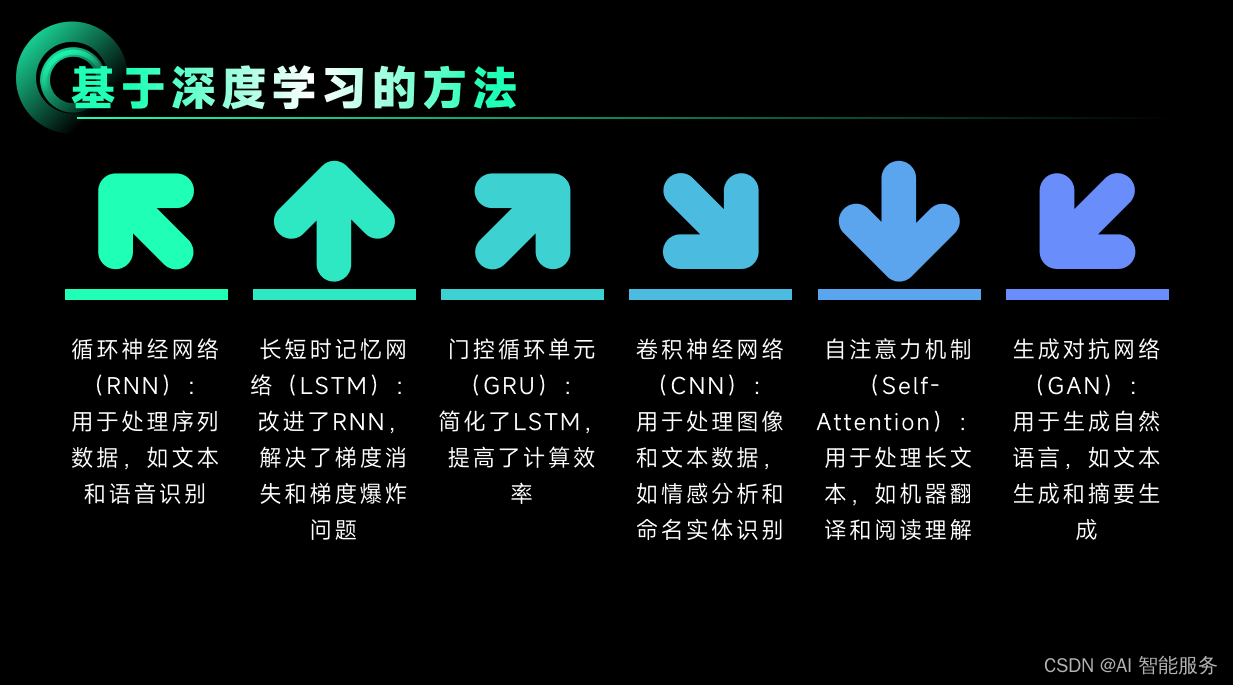
基础课2——自然语言处理
1.概念 自然语言处理(Natural Language Processing, NLP)是计算机科学领域与人工智能领域中的一个重要方向,它研究能实现人与计算机之间用自然语言进行有效通信的各种理论和方法。 自然语言处理的主要研究方向包括: 语言学研究&…...

有趣的GPT指令
1 从现在开始,你的回答必须把所有字替换emoji,并保持原来的含义。你不能使用任何汉字或英文。如果有不适当的词语,将它们替换成对应的emoji。下面是一个例子: 原文:爷吐啦 翻译:👴ὃ…...

小样本学习--(1)概论
目录 一、概述 二、小样本学习的数据集 1、Omniglot 2、MiniimageNet 三、孪生网络 四、三元组损失函数 一、概述 小样本学习用于处理训练数据集中样本数量少的情况,一般来说,小样本学习流程是这样的,从一个多种类少量样本的巨大数据集…...
数据结构之手撕顺序表(讲解➕源代码)
0.引言 在本章之后,就要求大家对于指针、结构体、动态开辟等相关的知识要熟练的掌握,如果有小伙伴对上面相关的知识还不是很清晰,要先弄明白再过来接着学习哦! 那进入正题,在讲解顺序表之前,我们先来介绍…...

小微企业是怎样从客户管理系统中获益的?
大企业普遍拥有成熟的客户管理系统,而对小微企业而言,客户管理系统的重要性更为突出。这是因为小微企业管理相对薄弱,资源有限,人力资金需要更加精细化的管理。那么,小微企业如何从客户管理系统中获益? 一…...

mysql整库备份表结构和数据
命令 mysqldump -P 端口 -h 主机 -u 用户名 -p 数据库 > xxxxbak.sql 将导出数据库的表结构及数据(建表语句和insert语句) 举例 mysqldump -P 3306 -h 100.120.56.23 -u my_username-p sys > system-230510.sql...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...

Golang dig框架与GraphQL的完美结合
将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用,可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器,能够帮助开发者更好地管理复杂的依赖关系,而 GraphQL 则是一种用于 API 的查询语言,能够提…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

Selenium常用函数介绍
目录 一,元素定位 1.1 cssSeector 1.2 xpath 二,操作测试对象 三,窗口 3.1 案例 3.2 窗口切换 3.3 窗口大小 3.4 屏幕截图 3.5 关闭窗口 四,弹窗 五,等待 六,导航 七,文件上传 …...

FFmpeg:Windows系统小白安装及其使用
一、安装 1.访问官网 Download FFmpeg 2.点击版本目录 3.选择版本点击安装 注意这里选择的是【release buids】,注意左上角标题 例如我安装在目录 F:\FFmpeg 4.解压 5.添加环境变量 把你解压后的bin目录(即exe所在文件夹)加入系统变量…...

多元隐函数 偏导公式
我们来推导隐函数 z z ( x , y ) z z(x, y) zz(x,y) 的偏导公式,给定一个隐函数关系: F ( x , y , z ( x , y ) ) 0 F(x, y, z(x, y)) 0 F(x,y,z(x,y))0 🧠 目标: 求 ∂ z ∂ x \frac{\partial z}{\partial x} ∂x∂z、 …...

2.2.2 ASPICE的需求分析
ASPICE的需求分析是汽车软件开发过程中至关重要的一环,它涉及到对需求进行详细分析、验证和确认,以确保软件产品能够满足客户和用户的需求。在ASPICE中,需求分析的关键步骤包括: 需求细化:将从需求收集阶段获得的高层需…...
