PA2019 Terytoria
洛谷P5987 [PA2019] Terytoria
题目大意
在一个平面直角坐标系上,有一个长度为 X X X,宽度为 Y Y Y的地图,这个地图的左边界和右边界是连通的,下边界和上边界也是连通的。
在地图中,有 X × Y X\times Y X×Y个格子以及 n n n个矩形,这些矩形的边与坐标轴平行。你只知道每个矩形两个对顶点的坐标,求被所有矩形覆盖住的格子数量的最大值?
1 ≤ n ≤ 5 × 1 0 5 , 2 ≤ X , Y ≤ 1 0 9 1\leq n\leq 5\times 10^5,2\leq X,Y\leq 10^9 1≤n≤5×105,2≤X,Y≤109
题解
因为每个矩形在横坐标上是取两边或中间,在纵坐标上也是取两边或中间,所以横坐标和纵坐标是不相关的。我们把这些矩形分成映射在 x x x轴的线段和映射在 y y y轴的线段,则最终的答案为 x x x轴上能被所有线段覆盖的最大长度 × y \times y ×y轴上能被所有线段覆盖的最大长度。那么,我们就可以将横坐标和纵坐标分开来做。
对横纵坐标进行离散化,对于离散化后的两个相邻的离散点连成的线段。那么,每种线段只有唯一的取法(取中间或者两边)才能覆盖这条由两个离散点连成的线段。我们用 01 01 01状态来表示每个矩形的覆盖情况( 0 0 0表示取两边, 1 1 1表示取中间),状态可以用哈希和差分来维护,然后用哈希表来存储对应状态的长度,边维护边取最大值。
时间复杂度为 O ( n log n + P ) O(n\log n+P) O(nlogn+P),其中 P P P为哈希表的大小。
code
#include<bits/stdc++.h>
using namespace std;
const int N=500000,P=19260817,base=7;
const long long mod1=998244353,mod2=1e9+7;
int n,X,Y,tot=0,l[2*N+5],r[P+5],hv[2*N+5],w1[2*N+5],w2[2*N+5];
long long re,ans=0,pw1[N+5],pw2[N+5];
struct node{int x,w,id;
}x[2*N+5],y[2*N+5];
bool cmp(node ax,node bx){return ax.x<bx.x;
}
void add(int x,int h1,int h2,int vt){l[++tot]=r[x];w1[tot]=h1;w2[tot]=h2;hv[tot]=vt;r[x]=tot;
}
void pl(int h1,int h2,int vt){int u=h1%P;for(int i=r[u];i;i=l[i]){if(w1[i]==h1&&w2[i]==h2){hv[i]+=vt;re=max(re,1ll*hv[i]);return;}}add(u,h1,h2,vt);re=max(re,1ll*vt);
}
long long solve(node *a,int mx){memset(r,0,sizeof(r));re=0;tot=0;long long h1=0,h2=0;pl(0,0,a[1].x);for(int i=1;i<2*n;i++){h1=(h1+pw1[a[i].id]*a[i].w+mod1)%mod1;h2=(h2+pw2[a[i].id]*a[i].w+mod2)%mod2;pl(h1,h2,a[i+1].x-a[i].x);}pl(0,0,mx-a[2*n].x);return re;
}
int main()
{
// freopen("globe.in","r",stdin);
// freopen("globe.out","w",stdout);scanf("%d%d%d",&n,&X,&Y);for(int i=1,dx,dy,ux,uy;i<=n;i++){scanf("%d%d%d%d",&dx,&dy,&ux,&uy);if(dx>ux) swap(dx,ux);if(dy>uy) swap(dy,uy);x[i*2-1]=(node){dx,1,i};x[i*2]=(node){ux,-1,i};y[i*2-1]=(node){dy,1,i};y[i*2]=(node){uy,-1,i};}sort(x+1,x+2*n+1,cmp);sort(y+1,y+2*n+1,cmp);pw1[0]=pw2[0]=1;for(int i=1;i<=N;i++){pw1[i]=pw1[i-1]*base%mod1;pw2[i]=pw2[i-1]*base%mod2;}ans=solve(x,X)*solve(y,Y);printf("%lld",ans);return 0;
}
相关文章:

PA2019 Terytoria
洛谷P5987 [PA2019] Terytoria 题目大意 在一个平面直角坐标系上,有一个长度为 X X X,宽度为 Y Y Y的地图,这个地图的左边界和右边界是连通的,下边界和上边界也是连通的。 在地图中,有 X Y X\times Y XY个格子以及…...

内容分发网络CDN分布式部署真的可以加速吗?原理是什么?
Cdn快不快?她为什么会快?同样的带宽为什么她会快?原理究竟是什么,同学们本着普及知识的想法,我了解的不是很深入,适合小白来看我的帖子,如果您是大佬还请您指正错误的地方,先谢谢大佬…...
微服务docker部署实战
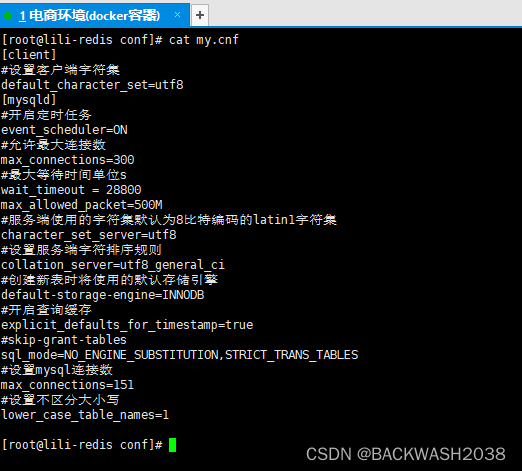
docker基础和进阶(*已掌握的可以跳过 *) 基础 docker基础 进阶 docker进阶 准备工作 提前准备好mysql和redis的配置,如下 在/zzq/mysql/conf目录下配置mysql配置文件my.cnf [client] #设置客户端字符集 default_character_setutf8 [mysqld] #开启定时任务 event_s…...

js实现拖拽功能
基于onMouseDown 、onMouseMove 、onMouseUp 使用 mousedown、mousemove 和 mouseup 事件来实现拖拽的基本思路是: 在 mousedown 事件中,开始追踪拖拽操作并记录鼠标按下的位置。 在 mousemove 事件中,根据鼠标的移动,更新被拖拽…...

数据库主从切换过程中Druid没法获取连接错误
背景: 今天dba在进行DB的主从切换,导致应用一直报错,获取不到DB连接,druid的错误信息如下: Could not open JDBC Connection for transaction; nested exception is com.alibaba.druid.pool.GetConnectionTimeoutExc…...
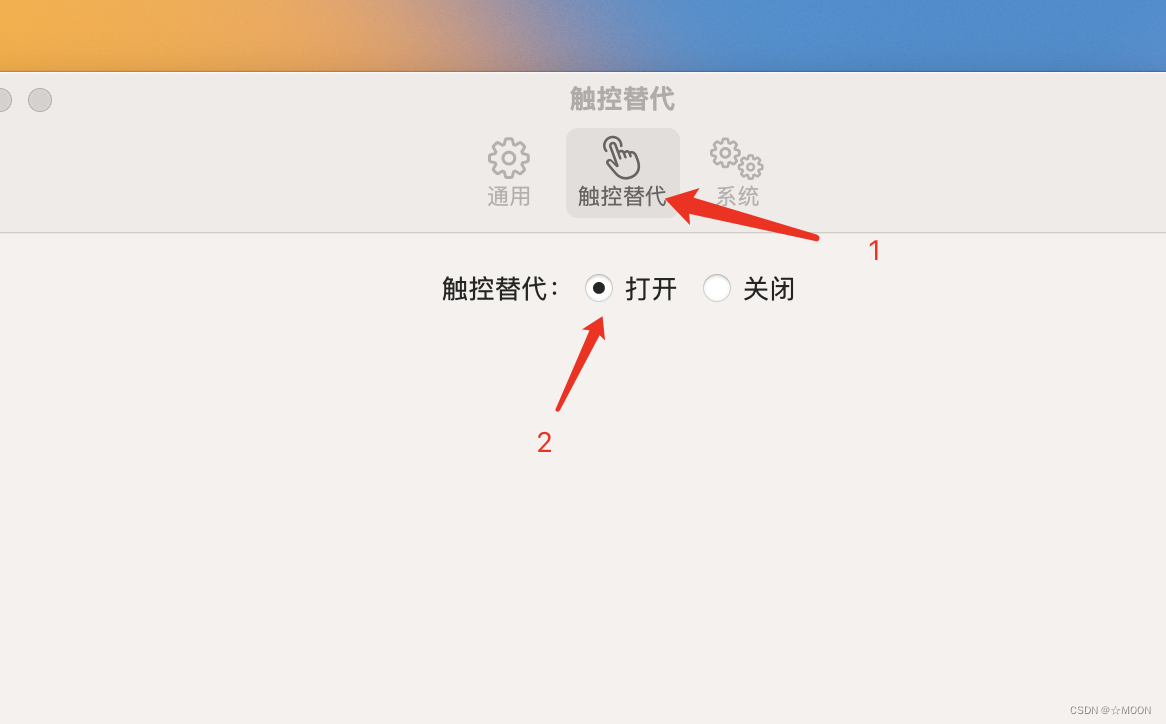
【iOS】Mac M1安装iPhone及iPad的app时设置问题
【iOS】Mac M1安装iPhone及iPad的app时设置问题 简介一,设置问题二,适配问题 简介 由于 苹果M1芯片的Mac可用安装iPhone以及iPad应用,因为开发者并没有适配Mac,因此产生了很多奇怪问题,这里总结归纳Mac M1安装iPhone和…...
Springboot 启动报错@spring.active@解析错误
Caused by: org.yaml.snakeyaml.scanner.ScannerException: while scanning for the next token found character that cannot start any token. (Do not use for indentation)in reader, line 10, column 13:active: spring.active^查看是否勾选...

【算法挨揍日记】day15——560. 和为 K 的子数组、974. 和可被 K 整除的子数组
560. 和为 K 的子数组 560. 和为 K 的子数组 题目描述: 给你一个整数数组 nums 和一个整数 k ,请你统计并返回 该数组中和为 k 的连续子数组的个数 。 子数组是数组中元素的连续非空序列。 解题思路: 我们可以很容易想到暴力解法…...

数字时代的探索与革新:Socks5代理的引领作用
在当今快速发展的数字时代,技术创新推动着社会的变革与进步。Socks5代理作为一项重要的网络技术,正引领着跨界电商、爬虫数据分析、企业全球化和游戏体验优化等领域的发展。本文将深入探讨Socks5代理技术在这些领域中的引领作用,以及它如何塑…...
算法-堆/归并排序-排序链表
算法-堆/归并排序-排序链表 1 题目概述 1.1 题目出处 https://leetcode.cn/problems/sort-list/description/?envTypestudy-plan-v2&envIdtop-interview-150 1.2 题目描述 2 优先级队列构建大顶堆 2.1 思路 优先级队列构建小顶堆链表所有元素放入小顶堆依次取出堆顶…...
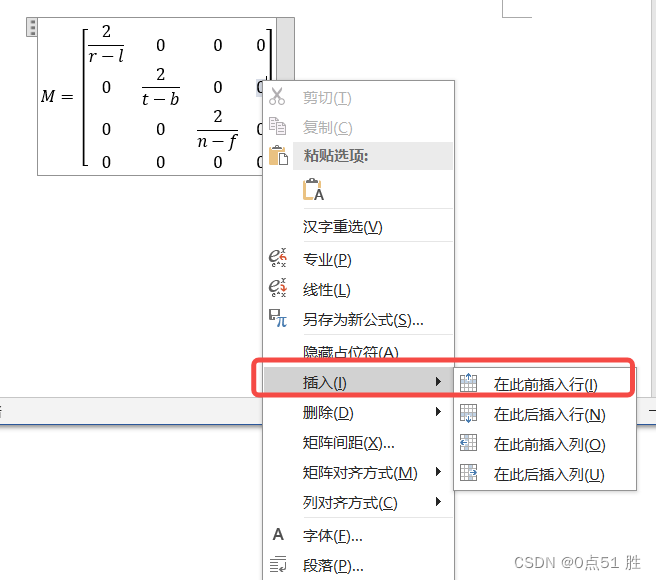
word 如何编写4x4矩阵
百度上给的教程,打印出来没有对齐 https://jingyan.baidu.com/article/6b182309995f8dba58e159fc.html 百度上的方式试了一下,不会对齐。导致公式看起来很奇怪。 下面方式会自动对齐 摸索了一下发现可以用下面这种方式编写 4x4 矩阵。先创建一个 3x3…...
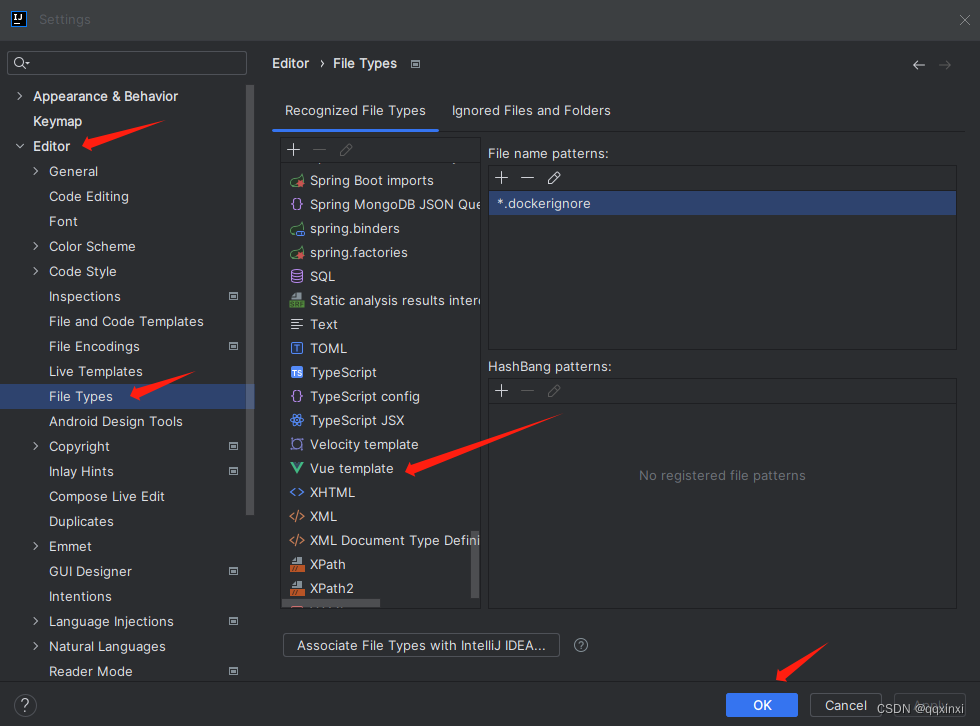
INTELlij IDEA编辑VUE项目
菜单中选择setting–>Plugins 或者快捷键 ctrlalts 搜索vue,但有些情况会搜索不出来,先说搜索到的情况 如下图所示: 如果没有vue.js则说明过去已经安装了。 搜索到了后点击Install安装即可, 但即使搜索成功了,也不…...
linux进程间通讯--信号量
1.认识信号量 方便理解:信号量就是一个计数器。当它大于0能用,小于等于0,用不了,这个值自己给。 2.特点: 信号量用于进程间同步,若要在进程间传递数据需要结合共享内存。信号量基于操作系统的 PV 操作&am…...

VS Code连接远程Linux服务器开发c++项目
1.在远程 Linux 上安装包 yum groupinstall "development tools" -y yum install cmake -y2.在 VSCode 上安装插件 C/CC/C Extension PackCMakeCMake ToolsCMake Language Support 3.连接远程Linux服务器...

stable diffusion的模型选择,采样器选择,关键词
一、Stable Diffusion的模型选择: 模型下载地址:https://civitai.com/,需要科学上网。 Deliberate:全能模型,prompt越详细生成的图片质量越好Realistic Vision:现实模型,生成仿真式图片&#…...

BI零售数据分析:以自身视角展开分析
随着零售业务不断扩展,市场竞争不断加剧,各层级的销售管理人员都急需一张能快速查看销售数据分析报表,能从中知道自己管辖内的业务最近或过去的情况,并依次为依据科学优化销售管理措施。这就要求零售数据分析报表信息足够多、数据…...
)
Maven 使用教程(三)
一、如何使用外部依赖项? 您可能已经注意到POM中的一个dependencies元素,我们一直在使用它作为示例。事实上,您一直在使用外部依赖项,但在这里我们将更详细地讨论它是如何工作的。有关更全面的介绍,请参阅我们的依赖机…...

行秋找工作的记录
2023-10-17 15:35-16:00 中移(苏州)研发中心面试 问了项目,还有一些我没准备到的Java八股文:Java类的加载过程,发射机制,redis存储结构,二叉平衡树等。但我也都没回答上来。应该无了。 2023-1…...
vue项目打包,使用externals抽离公共的第三方库
封装了一个插件,用来vue打包抽离公共的第三方库,使用unplugin进行插件开发,vite对应的功能使用了vite-plugin-externals进行二次开发 github地址 npm地址 hfex-auto-externals-plugin 自动注入插件,使用 unplugin 和 html-webpack-plugin进…...

九阳真经之各大厂校招
大学计算机系的同学要怎么努力才能校招进大厂? 秋招的大公司非常多,也是非常好的,赶上了秋招,你基本工作就敲定了,在整个应届毕业生的人群中你就占据很大的优势了。 如何准备应届校招? 一、做好规划,把…...

基于Flask实现的医疗保险欺诈识别监测模型
基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施,由雇主和个人按一定比例缴纳保险费,建立社会医疗保险基金,支付雇员医疗费用的一种医疗保险制度, 它是促进社会文明和进步的…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...

JUC笔记(上)-复习 涉及死锁 volatile synchronized CAS 原子操作
一、上下文切换 即使单核CPU也可以进行多线程执行代码,CPU会给每个线程分配CPU时间片来实现这个机制。时间片非常短,所以CPU会不断地切换线程执行,从而让我们感觉多个线程是同时执行的。时间片一般是十几毫秒(ms)。通过时间片分配算法执行。…...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...

Java面试专项一-准备篇
一、企业简历筛选规则 一般企业的简历筛选流程:首先由HR先筛选一部分简历后,在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如:Boss直聘(招聘方平台) 直接按照条件进行筛选 例如:…...

【Android】Android 开发 ADB 常用指令
查看当前连接的设备 adb devices 连接设备 adb connect 设备IP 断开已连接的设备 adb disconnect 设备IP 安装应用 adb install 安装包的路径 卸载应用 adb uninstall 应用包名 查看已安装的应用包名 adb shell pm list packages 查看已安装的第三方应用包名 adb shell pm list…...

Qt 事件处理中 return 的深入解析
Qt 事件处理中 return 的深入解析 在 Qt 事件处理中,return 语句的使用是另一个关键概念,它与 event->accept()/event->ignore() 密切相关但作用不同。让我们详细分析一下它们之间的关系和工作原理。 核心区别:不同层级的事件处理 方…...
