机器学习——奇异值分解二(特征分解+SVD纯理解)
矩阵的特征分解
特征值和特征向量的定义
抄来的:奇异值分解
困惑1:特征值和特征向量,和原矩阵是怎样的关系,需要一个栗子进行更具象的认识
困惑2:为什么多个特征向量组合成的矩阵,可以构成矩阵A的特征分解?需要推导
困惑3:为什么要特征向量标准化?
困惑4:标准正交基是什么,为什么满足 W T W = I W^TW=I WTW=I
为什么。。。。
太多why,只能自己来解决吗。。。涕泪横流。。。
先来看看特征值和特征向量
特征值与特征向量的推导
求解特征向量与特征值
A x = λ x Ax=λx Ax=λx,λ是特征值,但特征值可能会有多个,每个特征值都有对应的特征向量
根据 ( A − λ E ) x = 0 (A-λE)x=0 (A−λE)x=0,而需要x是非零向量,则要求A-λE的行列式为0,即 ∣ A − λ E ∣ = 0 |A-λE|=0 ∣A−λE∣=0,就可以求出多个λ值
分别将λ值代入 ∣ A − λ E ∣ x = 0 |A-λE|x=0 ∣A−λE∣x=0,就可以求出对应的特征向量x
question:为什么x是非零向量, ∣ A − λ E ∣ = 0 |A-λE|=0 ∣A−λE∣=0的行列式就为0呢?而不是 A − λ E = 0 A-λE=0 A−λE=0向量呢?
still,why?
毫不避讳地说:我大学线性代数是老师给的同情分,60分飘过
但我后来,有自己学习过的,现在也忘个精光了,现在还是重新梳理一遍吧,省的回头海马体又不争气
非零解与行列式值的关系
首先,先从求解矩阵的行列式方法,推导出【非零解与行列式值的关系】
求解行列式,要从【消元法】求解齐次方程组的权重系数w的过程讲起:
- w 1 x 11 + w 2 x 12 + w 3 x 13 = 0 w_1x_{11}+w_2x_{12}+w_3x_{13}=0 w1x11+w2x12+w3x13=0 式子①
- w 1 x 21 + w 2 x 22 + w 3 x 23 = 0 w_1x_{21}+w_2x_{22}+w_3x_{23}=0 w1x21+w2x22+w3x23=0 式子②
- w 1 x 31 + w 2 x 32 + w 3 x 33 = 0 w_1x_{31}+w_2x_{32}+w_3x_{33}=0 w1x31+w2x32+w3x33=0 式子③
通过消元法,求解 w 1 、 w 2 、 w 3 w_1、w_2、w_3 w1、w2、w3:
- 式子①保持: w 1 x 11 + w 2 x 12 + w 3 x 13 = 0 w_1x_{11}+w_2x_{12}+w_3x_{13}=0 w1x11+w2x12+w3x13=0
- 式子②【数乘】【数加】消去 w 1 w_1 w1项
- 数乘: w 1 x 21 x 11 x 21 + w 2 x 22 x 11 x 21 + w 3 x 23 x 11 x 21 = 0 w_1x_{21}\frac{x_{11}}{x_{21}}+w_2x_{22}\frac{x_{11}}{x_{21}}+w_3x_{23}\frac{x_{11}} {x_{21}}=0 w1x21x21x11+w2x22x21x11+w3x23x21x11=0
- 数加①: 式子② -式子①可得 w 1 ∗ 0 + w 2 ( x 22 x 11 x 21 − x 12 ) + w 3 ( x 23 x 11 x 21 − x 13 ) = 0 w_1*0+w_2(x_{22}\frac{x_{11}}{x_{21}}-x_{12})+w_3(x_{23}\frac{x_{11}}{x_{21}}-x_{13})=0 w1∗0+w2(x22x21x11−x12)+w3(x23x21x11−x13)=0
- 即简化为 w 1 ∗ 0 + w 2 b 2 + w 3 b 3 = 0 w_1*0+w_2b_{2}+w_3b_3=0 w1∗0+w2b2+w3b3=0
- 式子③【数乘】【数加】消去 w 1 、 w 2 w_1、w_2 w1、w2项
- 数乘: w 1 x 31 x 11 x 31 + w 2 x 32 x 11 x 31 + w 3 x 33 x 11 x 31 = y 3 x 11 x 31 w_1x_{31}\frac{x_{11}}{x_{31}}+w_2x_{32}\frac{x_{11}}{x_{31}}+w_3x_{33}\frac{x_{11}}{x_{31}}=y_3\frac{x_{11}}{x_{31}} w1x31x31x11+w2x32x31x11+w3x33x31x11=y3x31x11
- 数加①:式子③ -式子①可得 w 1 ∗ 0 + w 2 ( x 32 x 11 x 31 − x 12 ) + w 3 ( x 33 x 11 x 31 − x 13 ) = 0 w_1*0+w_2(x_{32}\frac{x_{11}}{x_{31}}-x_{12})+w_3(x_{33}\frac{x_{11}}{x_{31}}-x_{13})=0 w1∗0+w2(x32x31x11−x12)+w3(x33x31x11−x13)=0
- 数乘再数加消除 w 2 w2 w2,最终可化简为: w 1 ∗ 0 + w 2 ∗ 0 + w 3 c 3 = 0 w_1*0+w_2*0+w_3c_3=0 w1∗0+w2∗0+w3c3=0
通过消元法后:
稍微整理,下列的a\b\c系列都是已知数,求出w
- w 1 a 1 + w 2 a 2 + w 3 a 3 = 0 w_1a_1+w_2a_2+w_3a_3=0 w1a1+w2a2+w3a3=0
- w 1 ∗ 0 + w 2 b 2 + w 3 b 3 = 0 w_1*0+w_2b_{2}+w_3b_3=0 w1∗0+w2b2+w3b3=0
- w 1 ∗ 0 + w 2 ∗ 0 + w 3 c 3 = 0 w_1*0+w_2*0+w_3c_3=0 w1∗0+w2∗0+w3c3=0
这种情况下,方程只有无解,零解和非零解三种情况
将系数写成矩阵 ∣ a 1 a 2 a 3 0 b 2 b 3 0 0 c 3 ∣ \begin{vmatrix}a_{1}&a_{2}&a_{3}\\0&b_{2}&b_{3}\\0&0&c_{3}\\\end{vmatrix} a100a2b20a3b3c3 ,要使w1、w2、w3三个中有非零解,那就至少需要c3=0-
我觉得我在放屁。。。应该不是这样的,我再衡量衡量
还是偷别的up主教学吧
找个正解的线性代数(三)行列式的来历
好,即使上述关系能体现出,行列式不为零,则有非齐次线性方程组有非零解
但跟求特征根有什么关系呢? ( A − λ E ) x = 0 (A-λE)x=0 (A−λE)x=0
求特征根是求齐次线性方程组的解,但原本求行列式时的方程是非齐次方程组
特征根λ的行列式是:
∣ x 11 − λ x 12 x 13 x 21 x 22 − λ x 23 x 31 x 32 x 33 − λ ∣ \begin{vmatrix}x_{11}-λ&x_{12}&x_{13}\\x_{21}&x_{22}-λ&x_{23}\\x_{31}&x_{32}&x_{33}-λ\\\end{vmatrix} x11−λx21x31x12x22−λx32x13x23x33−λ
然后我又去翻其他的资料,果然。。。前边的分析方向搞错了,只能证明非齐次线性方程组的非零解条件是:行列式≠0

继续论证,齐次线性方程组的非零解条件是:行列式=0,才能说明行列式与特征根的关系



所以,求解非零特征根,是要求齐次线性方程组对应的系数矩阵的秩小于元素个数,也就等同于矩阵的行列式为0。
衍生出新的问题:为什么行列式是这样算的,行列式的本质到底是什么?它的计算有什么代数或几何意义吗?
我觉得,我需要知道它。。。然后去找到知乎一篇文行列式本质
我粗看一遍,感觉这篇文章一定藏着我想要的答案,但首先,我要能看懂它…
我很绝望,行列式的定义是总结归纳出来的吗?
它没有个因果关系吗?
头疼。。。。。
任意矩阵,都可以通过【交换】、【倍乘】、【倍加】的方式,变成上三角矩阵,且不改变行列式的值
B站up主的俗说矩阵,非常好!

穿插理解:行列式
呜呜呜呜呜呜,经过我坚持不懈地在B站摸鱼划水,终于在众说纷纭中,打通了任督二脉
我好像是懂了,懂了n阶行列式的定义,为什么是这样的了!!!!
先摆上二阶行列式的定义:
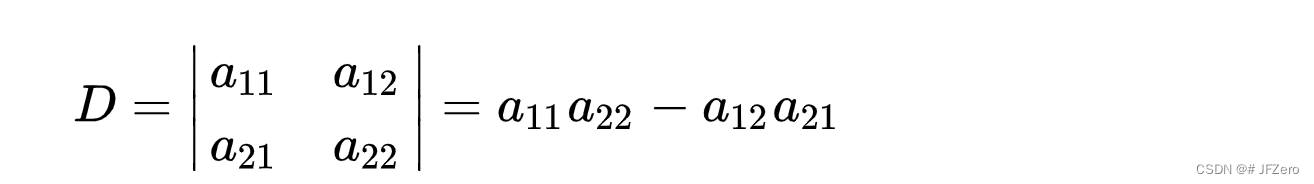
再摆上三阶行列式的定义:
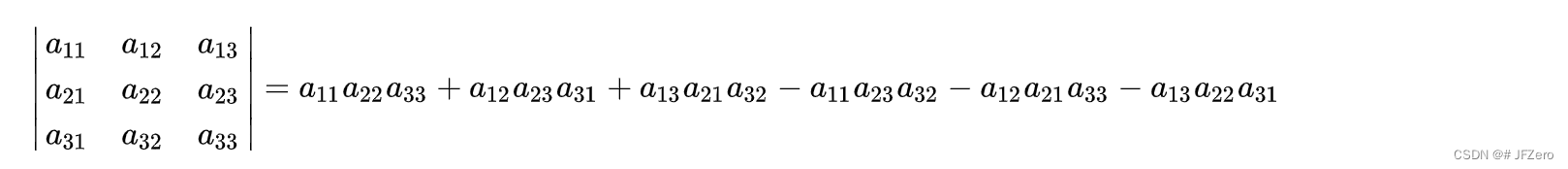
再摆上n阶行列式的定义:

I don’t know why,how,what
二阶、二阶推导到三阶,我还能理解,但是怎么推出n阶的???
非常头疼,看了很多解释,有些看起来很专业,但我还是不理解
直到回顾到B站的俗说矩阵的行列式按行按列展开
我才有种灵光一闪的开窍!!!哦!!!!
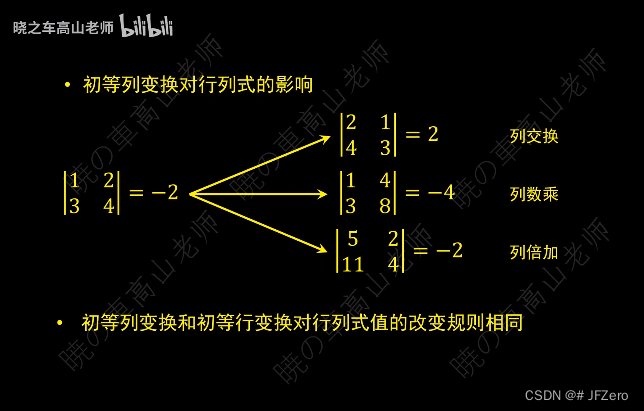
首先,在行列式的二、三阶定义中,可以推导出【数乘】【交换】【数加】三种变换时的行列式变化
- 【行或列数加】:行列式值无改变
- 【行或列数乘】:行列式值乘相同数
- 【行或列相邻交换】:行列式值为相反值
二阶可以由余子式累加得到
通过拆分成三角形式的行列式,可以更好地求的行列式
∣ a b x 21 x 22 ∣ = ∣ a 0 x 21 x 22 ∣ + ∣ 0 b x 21 x 22 ∣ \begin{vmatrix}a&b\\x_{21}&x_{22}\\\end{vmatrix}=\begin{vmatrix}a&0\\x_{21}&x_{22}\\\end{vmatrix}+\begin{vmatrix}0&b\\x_{21}&x_{22}\\\end{vmatrix} ax21bx22 = ax210x22 + 0x21bx22
下三角无需更换行列,直接求得行列式
∣ a 0 x 21 x 22 ∣ = a ∣ x 22 ∣ = a x 22 \begin{vmatrix}a&0\\x_{21}&x_{22}\\\end{vmatrix}=a\begin{vmatrix}x_{22}\\\end{vmatrix}=ax_{22} ax210x22 =a x22 =ax22
将行列式通过【变换】,变换成下三角后,再求行列式
∣ 0 b x 21 x 22 ∣ = − ∣ b 0 x 22 x 21 ∣ = − b ∣ x 21 ∣ = − b x 21 \begin{vmatrix}0&b\\x_{21}&x_{22}\\\end{vmatrix}=-\begin{vmatrix}b&0\\x_{22}&x_{21}\\\end{vmatrix}=-b\begin{vmatrix}x_{21}\\\end{vmatrix}=-bx_{21} 0x21bx22 =− bx220x21 =−b x21 =−bx21
相邻变换,行列式值会变为相反值,因此变换过程有负号产生
三阶也是如此,但三阶是可以由二阶推导来的
∣ x 11 x 12 x 13 x 21 x 22 x 23 x 31 x 32 x 33 ∣ = ∣ x 11 0 0 x 21 x 22 x 23 x 31 x 32 x 33 ∣ + ∣ 0 x 12 0 x 21 x 22 x 23 x 31 x 32 x 33 ∣ + ∣ 0 0 x 13 x 21 x 22 x 23 x 31 x 32 x 33 ∣ \begin{vmatrix}x_{11}&x_{12}&x_{13}\\x_{21}&x_{22}&x_{23}\\x_{31}&x_{32}&x_{33}\\\end{vmatrix}=\begin{vmatrix}x_{11}&0&0\\x_{21}&x_{22}&x_{23}\\x_{31}&x_{32}&x_{33}\\\end{vmatrix} +\begin{vmatrix}0&x_{12}&0\\x_{21}&x_{22}&x_{23}\\x_{31}&x_{32}&x_{33}\\\end{vmatrix}+\begin{vmatrix}0&0&x_{13}\\x_{21}&x_{22}&x_{23}\\x_{31}&x_{32}&x_{33}\\\end{vmatrix} x11x21x31x12x22x32x13x23x33 = x11x21x310x22x320x23x33 + 0x21x31x12x22x320x23x33 + 0x21x310x22x32x13x23x33
第一个直接构成下三角
- ∣ x 11 0 0 x 21 x 22 x 23 x 31 x 32 x 33 ∣ = x 11 ∣ x 22 x 23 x 32 x 33 ∣ = x 11 ∣ x 22 0 x 32 x 33 ∣ + x 11 ∣ 0 x 23 x 32 x 33 ∣ \begin{vmatrix}x_{11}&0&0\\x_{21}&x_{22}&x_{23}\\x_{31}&x_{32}&x_{33}\\\end{vmatrix}=x_{11}\begin{vmatrix}x_{22}&x_{23}\\x_{32}&x_{33}\\\end{vmatrix}=x_{11}\begin{vmatrix}x_{22}&0\\x_{32}&x_{33}\\\end{vmatrix}+x_{11}\begin{vmatrix}0&x_{23}\\x_{32}&x_{33}\\\end{vmatrix} x11x21x310x22x320x23x33 =x11 x22x32x23x33 =x11 x22x320x33 +x11 0x32x23x33
- x 11 ∣ x 22 0 x 32 x 33 ∣ + x 11 ∣ 0 x 23 x 32 x 33 ∣ = x 11 ∣ x 22 0 x 32 x 33 ∣ − x 11 ∣ x 23 0 x 33 x 32 ∣ x_{11}\begin{vmatrix}x_{22}&0\\x_{32}&x_{33}\\\end{vmatrix}+x_{11}\begin{vmatrix}0&x_{23}\\x_{32}&x_{33}\\\end{vmatrix}=x_{11}\begin{vmatrix}x_{22}&0\\x_{32}&x_{33}\\\end{vmatrix}-x_{11}\begin{vmatrix}x_{23}&0\\x_{33}&x_{32}\\\end{vmatrix} x11 x22x320x33 +x11 0x32x23x33 =x11 x22x320x33 −x11 x23x330x32
- 最终得到: x 11 ∗ x 22 x 33 − x 11 x 23 x 32 x_{11}*x_{22}x_{33}-x_{11}x_{23}x_{32} x11∗x22x33−x11x23x32
第二个需要变换1次,才成为下三角
- ∣ 0 x 12 0 x 21 x 22 x 23 x 31 x 32 x 33 ∣ = − ∣ x 12 0 0 x 22 x 21 x 23 x 32 x 31 x 33 ∣ = − x 12 ∣ x 21 x 23 x 31 x 33 ∣ \begin{vmatrix}0&x_{12}&0\\x_{21}&x_{22}&x_{23}\\x_{31}&x_{32}&x_{33}\\\end{vmatrix}=-\begin{vmatrix}x_{12}&0&0\\x_{22}&x_{21}&x_{23}\\x_{32}&x_{31}&x_{33}\\\end{vmatrix}=-x_{12}\begin{vmatrix}x_{21}&x_{23}\\x_{31}&x_{33}\\\end{vmatrix} 0x21x31x12x22x320x23x33 =− x12x22x320x21x310x23x33 =−x12 x21x31x23x33
- − x 12 ∣ x 21 x 23 x 31 x 33 ∣ = − x 12 ( ∣ x 21 0 x 31 x 33 ∣ + ∣ 0 x 23 x 31 x 33 ∣ ) = − x 12 ( ∣ x 21 0 x 31 x 33 ∣ − ∣ x 23 0 x 33 x 31 ∣ ) = − x 12 ∗ ( x 21 ∗ ∣ x 33 ∣ − x 23 ∗ ∣ x 31 ∣ ) = − x 12 ∗ x 21 ∗ x 33 + x 12 ∗ x 23 ∗ x 31 -x_{12}\begin{vmatrix}x_{21}&x_{23}\\x_{31}&x_{33}\\\end{vmatrix}= -x_{12}(\begin{vmatrix}x_{21}&0\\x_{31}&x_{33}\\\end{vmatrix}+\begin{vmatrix}0&x_{23}\\x_{31}&x_{33}\\\end{vmatrix}) =-x_{12}(\begin{vmatrix}x_{21}&0\\x_{31}&x_{33}\\\end{vmatrix}-\begin{vmatrix}x_{23}&0\\x_{33}&x_{31}\\\end{vmatrix}) =-x_{12}*(x_{21}*\begin{vmatrix}x_{33}\\\end{vmatrix}-x_{23}*\begin{vmatrix}x_{31}\\\end{vmatrix})=-x_{12}*x_{21}*x_{33}+x_{12}*x_{23}*x_{31} −x12 x21x31x23x33 =−x12( x21x310x33 + 0x31x23x33 )=−x12( x21x310x33 − x23x330x31 )=−x12∗(x21∗ x33 −x23∗ x31 )=−x12∗x21∗x33+x12∗x23∗x31
第三个需要变换2次,才成为下三角
- ∣ 0 0 x 13 x 21 x 22 x 23 x 31 x 32 x 33 ∣ = − ∣ 0 x 13 0 x 21 x 23 x 22 x 31 x 33 x 32 ∣ = ∣ x 13 0 0 x 23 x 21 x 22 x 33 x 31 x 32 ∣ = x 13 ∣ x 21 x 22 x 31 x 32 ∣ \begin{vmatrix}0&0&x_{13}\\x_{21}&x_{22}&x_{23}\\x_{31}&x_{32}&x_{33}\\\end{vmatrix} =-\begin{vmatrix}0&x_{13}&0\\x_{21}&x_{23}&x_{22}\\x_{31}&x_{33}&x_{32}\\\end{vmatrix} =\begin{vmatrix}x_{13}&0&0\\x_{23}&x_{21}&x_{22}\\x_{33}&x_{31}&x_{32}\\\end{vmatrix} =x_{13}\begin{vmatrix}x_{21}&x_{22}\\x_{31}&x_{32}\\\end{vmatrix} 0x21x310x22x32x13x23x33 =− 0x21x31x13x23x330x22x32 = x13x23x330x21x310x22x32 =x13 x21x31x22x32
- 同理可推导得: x 13 ∗ x 21 ∗ x 32 − x 13 ∗ x 22 ∗ x 32 x_{13}*x_{21}*x_{32}-x_{13}*x_{22}*x_{32} x13∗x21∗x32−x13∗x22∗x32
为什么要变换的这么详细呢?因为这个过程,恰好展现了n阶行列式的定义!
首先,每一次的变换,都是先把首行中的元素,逐一变换到左上角,这个变换的过程主要与列有关
如果首行元素在奇数列(如第3列),则变换到左上角时,行列式值是不变号的
如果首行元素在偶数列(如第2列),则变换到左上角时,行列式值会变成负号

但除了首行元素的列问题,还有次行元素的列问题
因此,我脑子不够用了,但好在世界上有很多优秀的阿婆主,能讲清楚一些
n阶特征公式解释
具体的,还是看up主的分析会比较有领悟
当然,可能我只是哦!但实际还不是很清晰,但。。。不想特别去深究行列式的定义,大概理解就好
我。。。又快要忘记前边思考的是什么问题了
已理解:行列式是什么,行列式和非零解的关系,可知道当行列式不为零时,求解特征值时,特征值也是非零解
特征值和特征向量的推导
如果从坐标系固定,矩阵向量变换的角度看,矩阵A与向量x相乘 A x Ax Ax,通常是对向量x进行【旋转】+【伸缩】的变换,这个变换过程中,并伴随有【升降维】的作用。
如果从矩阵向量固定,坐标系变换的角度看,矩阵A与向量x相乘 A x Ax Ax,则表示向量x是在A坐标系下,(相当于声明:x是火星A上的人)
而矩阵与特征向量、特征值的关系 A x = λ x Ax=λx Ax=λx,右侧的 λ x λx λx没有矩阵相乘,则表示标准正交基坐标系 I I I下的向量x,只不过这个向量x中每个值都乘以λ倍
而 A x = λ x Ax=λx Ax=λx,则表示,在A坐标系下的特征向量x,实际等同于标准正交基坐标系 I I I里的向量x伸缩λ倍,相当于当坐标系A旋转伸缩变换成标准正交基坐标系 I I I后,向量x的方向没有发生旋转,只是进行了伸缩变换。
向量x,正是特征向量,而特征值λ相当于向量x伸缩的倍数
例如A有一个特征向量 x 1 x_1 x1及对应特征值 λ 1 λ_1 λ1,则 A x 1 = λ 1 x 1 Ax_1=λ_1x_1 Ax1=λ1x1
∣ a 11 x 12 a 13 a 21 a 22 a 23 a 31 a 32 a 33 ∣ ∣ x 11 x 21 x 31 ∣ = λ 1 ∣ x 11 x 21 x 31 ∣ \begin{vmatrix}a_{11}&x_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\\\end{vmatrix}\begin{vmatrix}x_{11}\\x_{21}\\x_{31}\\\end{vmatrix}=λ_1\begin{vmatrix}x_{11}\\x_{21}\\x_{31}\\\end{vmatrix} a11a21a31x12a22a32a13a23a33 x11x21x31 =λ1 x11x21x31
再例如A的第2 个特征向量 x 2 x_2 x2及对应特征值 λ 2 λ_2 λ2,则 A x 2 = λ 2 x 2 Ax_2=λ_2x_2 Ax2=λ2x2
∣ a 11 x 12 a 13 a 21 a 22 a 23 a 31 a 32 a 33 ∣ ∣ x 12 x 22 x 32 ∣ = λ 1 ∣ x 12 x 22 x 32 ∣ \begin{vmatrix}a_{11}&x_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\\\end{vmatrix}\begin{vmatrix}x_{12}\\x_{22}\\x_{32}\\\end{vmatrix}=λ_1\begin{vmatrix}x_{12}\\x_{22}\\x_{32}\\\end{vmatrix} a11a21a31x12a22a32a13a23a33 x12x22x32 =λ1 x12x22x32
将A的所有特征向量x组成矩阵W,则有
W = ∣ x 11 x 12 x 13 x 21 x 22 x 23 x 31 x 32 x 33 ∣ W=\begin{vmatrix}x_{11}&x_{12}&x_{13}\\x_{21}&x_{22}&x_{23}\\x_{31}&x_{32}&x_{33}\\\end{vmatrix} W= x11x21x31x12x22x32x13x23x33
要让 λ 1 、 λ 2 、 λ 3 λ_1、λ_2、λ_3 λ1、λ2、λ3对应乘以到W中,则需要将λ形成对角矩阵
Σ = ∣ λ 1 0 0 0 λ 2 0 0 0 λ 3 ∣ Σ=\begin{vmatrix}λ_1&0&0\\0&λ_2&0\\0&0&λ_3\\\end{vmatrix} Σ= λ1000λ2000λ3
则 W Σ = ∣ λ 1 x 11 λ 2 x 12 λ 3 x 13 λ 1 x 21 λ 2 x 22 λ 3 x 23 λ 1 x 31 λ 2 x 32 λ 3 x 33 ∣ WΣ=\begin{vmatrix}λ_1x_{11}&λ_2x_{12}&λ_3x_{13}\\λ_1x_{21}&λ_2x_{22}&λ_3x_{23}\\λ_1x_{31}&λ_2x_{32}&λ_3x_{33}\\\end{vmatrix} WΣ= λ1x11λ1x21λ1x31λ2x12λ2x22λ2x32λ3x13λ3x23λ3x33
而 A W = ∣ a 11 x 12 a 13 a 21 a 22 a 23 a 31 a 32 a 33 ∣ ∣ x 11 x 12 x 13 x 21 x 22 x 23 x 31 x 32 x 33 ∣ = W Σ = ∣ x 11 x 12 x 13 x 21 x 22 x 23 x 31 x 32 x 33 ∣ ∣ λ 1 0 0 0 λ 2 0 0 0 λ 3 ∣ AW=\begin{vmatrix}a_{11}&x_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\\\end{vmatrix}\begin{vmatrix}x_{11}&x_{12}&x_{13}\\x_{21}&x_{22}&x_{23}\\x_{31}&x_{32}&x_{33}\\\end{vmatrix}=WΣ=\begin{vmatrix}x_{11}&x_{12}&x_{13}\\x_{21}&x_{22}&x_{23}\\x_{31}&x_{32}&x_{33}\\\end{vmatrix}\begin{vmatrix}λ_1&0&0\\0&λ_2&0\\0&0&λ_3\\\end{vmatrix} AW= a11a21a31x12a22a32a13a23a33 x11x21x31x12x22x32x13x23x33 =WΣ= x11x21x31x12x22x32x13x23x33 λ1000λ2000λ3
A W W − 1 = W Σ W − 1 AWW^{-1}=WΣW^{-1} AWW−1=WΣW−1,因此就有 A = W Σ W − 1 A=WΣW^{-1} A=WΣW−1
这就是矩阵特征分解的推导
因此,一个矩阵,可以由它的所有特征向量和特征值来表示
矩阵特征分解的意义
矩阵(方阵),可以由它的所有特征向量和特征值来表示,
例如A是mxm的方阵,它所有的特征向量为mxm的方阵W,对应的特征值矩阵为mxm的对角矩阵Σ
则 A = W Σ W T A = WΣW^T A=WΣWT
特征分解后,可以选择删除一些不重要的特征,对方阵A进行降维。
那怎么知道哪些特征是不重要的呢?
这里的特征,其实指的就是特征向量和特征值,主要看特征值。
如果特征值相对而言特别特别小,接近于0,则这个特征向量对原方阵A的影响相应比较小。
A = ∣ a 11 x 12 a 13 a 21 a 22 a 23 a 31 a 32 a 33 ∣ = ∣ x 11 x 12 x 13 x 21 x 22 x 23 x 31 x 32 x 33 ∣ ∣ λ 1 0 0 0 λ 2 0 0 0 λ 3 ∣ ∣ x 11 x 21 x 31 x 12 x 22 x 32 x 13 x 23 x 33 ∣ A=\begin{vmatrix}a_{11}&x_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\\\end{vmatrix}=\begin{vmatrix}x_{11}&x_{12}&x_{13}\\x_{21}&x_{22}&x_{23}\\x_{31}&x_{32}&x_{33}\\\end{vmatrix}\begin{vmatrix}λ_1&0&0\\0&λ_2&0\\0&0&λ_3\\\end{vmatrix}\begin{vmatrix}x_{11}&x_{21}&x_{31}\\x_{12}&x_{22}&x_{32}\\x_{13}&x_{23}&x_{33}\\\end{vmatrix} A= a11a21a31x12a22a32a13a23a33 = x11x21x31x12x22x32x13x23x33 λ1000λ2000λ3 x11x12x13x21x22x23x31x32x33
A = ∣ λ 1 x 11 λ 2 x 12 λ 3 x 13 λ 1 x 21 λ 2 x 22 λ 3 x 23 λ 1 x 31 λ 2 x 32 λ 3 x 33 ∣ ∣ x 11 x 21 x 31 x 12 x 22 x 32 x 13 x 23 x 33 ∣ A=\begin{vmatrix}λ_1x_{11}&λ_2x_{12}&λ_3x_{13}\\λ_1x_{21}&λ_2x_{22}&λ_3x_{23}\\λ_1x_{31}&λ_2x_{32}&λ_3x_{33}\\\end{vmatrix}\begin{vmatrix}x_{11}&x_{21}&x_{31}\\x_{12}&x_{22}&x_{32}\\x_{13}&x_{23}&x_{33}\\\end{vmatrix} A= λ1x11λ1x21λ1x31λ2x12λ2x22λ2x32λ3x13λ3x23λ3x33 x11x12x13x21x22x23x31x32x33
A = ∣ λ 1 x 11 2 + λ 2 x 12 2 + λ 3 x 13 2 λ 1 x 11 x 21 + λ 2 x 12 x 22 + λ 3 x 13 x 23 λ 1 x 11 x 31 + λ 2 x 12 x 32 + λ 3 x 13 x 33 λ 1 x 21 x 11 + λ 2 x 22 x 12 + λ 3 x 23 x 13 λ 1 x 21 x 21 + λ 2 x 22 x 22 + λ 3 x 23 x 23 λ 1 x 21 x 31 + λ 2 x 22 x 32 + λ 3 x 32 x 33 λ 1 x 31 x 11 + λ 2 x 32 x 12 + λ 3 x 33 x 13 λ 1 x 31 x 21 + λ 2 x 32 x 22 + λ 3 x 33 x 23 λ 1 x 31 x 31 + λ 2 x 32 x 32 + λ 3 x 33 x 33 ∣ A=\begin{vmatrix} λ_1x^2_{11}+λ_2x^2_{12}+λ_3x^2_{13} &λ_1x_{11}x_{21}+λ_2x_{12}x_{22}+λ_3x_{13}x_{23} &λ_1x_{11}x_{31}+λ_2x_{12}x_{32}+λ_3x_{13}x_{33}\\ λ_1x_{21}x_{11}+λ_2x_{22}x_{12}+λ_3x_{23}x_{13} &λ_1x_{21}x_{21}+λ_2x_{22}x_{22}+λ_3x_{23}x_{23} &λ_1x_{21}x_{31}+λ_2x_{22}x_{32}+λ_3x_{32}x_{33}\\ λ_1x_{31}x_{11}+λ_2x_{32}x_{12}+λ_3x_{33}x_{13} &λ_1x_{31}x_{21}+λ_2x_{32}x_{22}+λ_3x_{33}x_{23} &λ_1x_{31}x_{31}+λ_2x_{32}x_{32}+λ_3x_{33}x_{33}\\\end{vmatrix} A= λ1x112+λ2x122+λ3x132λ1x21x11+λ2x22x12+λ3x23x13λ1x31x11+λ2x32x12+λ3x33x13λ1x11x21+λ2x12x22+λ3x13x23λ1x21x21+λ2x22x22+λ3x23x23λ1x31x21+λ2x32x22+λ3x33x23λ1x11x31+λ2x12x32+λ3x13x33λ1x21x31+λ2x22x32+λ3x32x33λ1x31x31+λ2x32x32+λ3x33x33
如果将特征值非常小的特征值和对应的特征向量去掉,如删掉λ1和x2,则有
A = ∣ λ 2 x 12 λ 3 x 13 λ 2 x 22 λ 3 x 23 λ 2 x 32 λ 3 x 33 ∣ ∣ x 12 x 22 x 32 x 13 x 23 x 33 ∣ A = \begin{vmatrix}λ_2x_{12}&λ_3x_{13}\\λ_2x_{22}&λ_3x_{23}\\λ_2x_{32}&λ_3x_{33}\\\end{vmatrix}\begin{vmatrix}x_{12}&x_{22}&x_{32}\\x_{13}&x_{23}&x_{33}\\\end{vmatrix} A= λ2x12λ2x22λ2x32λ3x13λ3x23λ3x33 x12x13x22x23x32x33
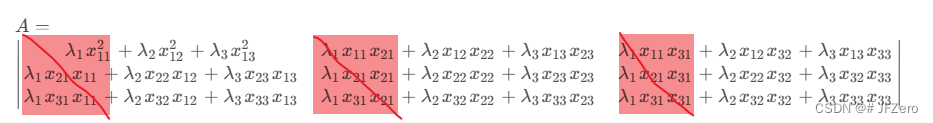
这样还原出来的A,就不是完完全全的A矩阵了,但相对而言,如果λ1比较小,那么还原出来的矩阵与A矩阵差别也不会太大
奇异值分解SVD
看过一个推导的非常详实的知乎大神:奇异值分解(SVD)
看过理解,不代表真的理解,自己去推导一下吧,搞不好会有一些新的认识
A是mxn的矩阵,U是mxm的方阵,V是nxn的方阵,∑是一个mxn的矩阵,且只有对角线上的元素为非零元素。
那么A、U、V、∑之间有什么关系,才能形成奇异值分解 A = U Σ V T A=UΣV^T A=UΣVT的关系呢?
首先,U是 A A T AA^T AAT方阵的特征向量,特征值为 λ u λ_u λu: A A T U = λ u U AA^TU=λ_uU AATU=λuU
其次,V是 A T A A^TA ATA方阵的特征向量,特征值为 λ v λ_v λv: A T A V = λ v V A^TAV=λ_vV ATAV=λvV
要知道,不同特征值对应的特征向量是线性无关的,因此,它的转置乘以它本身 V T V = U T U = E V^TV=U^TU=E VTV=UTU=E
进而,可以求出奇异矩阵∑, A = U Σ V T → A V = U Σ V T V = U Σ A=UΣV^T→AV=UΣV^TV=UΣ A=UΣVT→AV=UΣVTV=UΣ
Σ Σ Σ只有对角线上的元素是非零,因此逐一求出对角线上的元素 α i α_i αi即可
A v 1 = U α 1 Av_1=Uα_1 Av1=Uα1、 A v 2 = U α 2 Av_2=Uα_2 Av2=Uα2…
又或者, A = U Σ V T → A T = V Σ U T A=UΣV^T→A^T=VΣU^T A=UΣVT→AT=VΣUT, A A T = U Σ V T V Σ U T = U Σ 2 U T AA^T=UΣV^TVΣU^T=UΣ^2U^T AAT=UΣVTVΣUT=UΣ2UT
由于U是 A A T AA^T AAT的特征向量,因此 A A T U = λ u U → A A T = U Σ u U T = U Σ 2 U T AA^TU=λ_uU→AA^T=UΣ_uU^T=UΣ^2U^T AATU=λuU→AAT=UΣuUT=UΣ2UT
因此有 Σ 2 = Σ u Σ^2=Σ_u Σ2=Σu,奇异值²=特征值
奇异值可以直接通过特征值开根号得到。
奇异值分解的降维意义
为什么奇异值分解,可以进行降维呢?
主要还是参考矩阵的特征分解时的降维意义。
不过,这只是一种比较数理方面的解释,B站有个博主,用了非常生动形象的动画效果,演示了降维的操作及意义!
B站小学长课堂
当时我在高铁的渣渣网络上看到时,虽然卡的一匹,但依然惊叹到:世间有如此博主,实乃学渣之幸事!
总之,到这里,奇异值分解内容,算是学习结束了
撒花~🌼
相关文章:
机器学习——奇异值分解二(特征分解+SVD纯理解)
矩阵的特征分解 特征值和特征向量的定义 抄来的:奇异值分解 困惑1:特征值和特征向量,和原矩阵是怎样的关系,需要一个栗子进行更具象的认识 困惑2:为什么多个特征向量组合成的矩阵,可以构成矩阵A的特征分解…...

牛客:FZ35 滑动窗口最小值
FZ35 滑动窗口最小值 文章目录 FZ35 滑动窗口最小值题目描述题解思路题解代码 题目描述 题解思路 遍历数组,然后遍历窗口找到最小值,加入到结果集里面 题解代码 func minSlidingWindow( nums []int , k int ) []int {// write code heren : len(nums…...
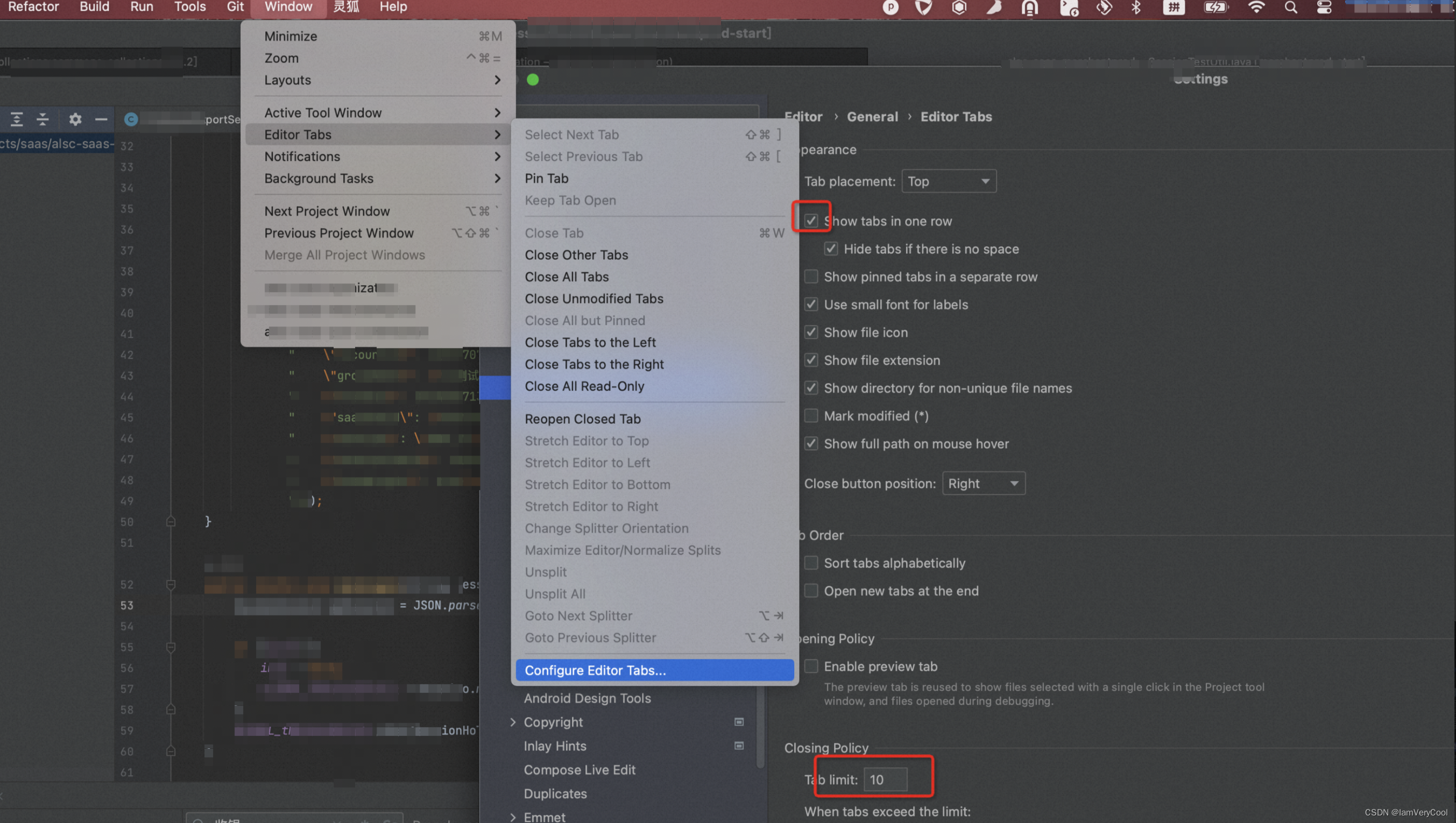
MAC上设置IDEA如何一个窗口打开多个项目,多个tab
1、IDEA一个窗口打开多个项目 如果你打开了多个项目、每次切换都要半天,想让项目都汇聚到top栏 点击 Window - Merge All Project Windows 即可 但是这样比较挫,每次打开新的项目都还是会重新打开一个IDEA窗口 so,如何设置项目在同一个窗口…...
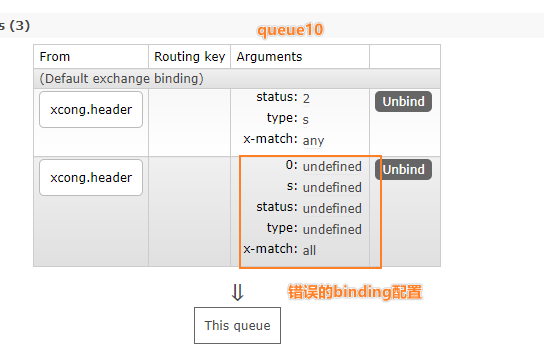
【学习笔记】RabbitMQ02:交换机,以及结合springboot快速开始
参考资料 RabbitMQ官方网站RabbitMQ官方文档噼咔噼咔-动力节点教程 文章目录 四、RabbitMQ :Exchange 交换机4.1 交换机类型4.2 扇形交换机 Fanout Exchange4.2.1 概念4.2.1 实例:生产者4.2.1.1 添加起步依赖4.2.1.2 配置文件4.2.1.3 JavaBean进行配置4.…...

【Python机器学习】零基础掌握OPTICS聚类
你是否曾经困扰于这样的如何将相似的商品以最优的方式推荐给你的客户? 假设你是一个电商网站的运营经理,有成千上万的商品和用户,但不知道如何有效地将相似的商品分组以便推荐。或者是一个环保组织的数据分析师,希望找出那些具有相似环境影响的地区。这些问题都需要一种可…...

【HuggingFace文档学习】Bert的token分类与句分类
BERT特性: BERT的嵌入是位置绝对(position absolute)的。BERT擅长于预测掩码token和NLU,但是不擅长下一文本生成。 1.BertForTokenClassification 一个用于token级分类的模型,可用于命名实体识别(NER)、部分语音标记…...
)
354 俄罗斯套娃信封问题(贪心+二分)
题目 链接 给你一个二维整数数组 envelopes ,其中 envelopes[i] [wi, hi] ,表示第 i 个信封的宽度和高度。 当另一个信封的宽度和高度都比这个信封大的时候,这个信封就可以放进另一个信封里,如同俄罗斯套娃一样。 请计算 最多…...

Vue页面结构
Vue页面结构 App.vue <!--html标签--> <template><div><h1>饿了么?</h1></div><HelloWorld msg"Vite Vue" /> </template> <!--js代码 vue3的语法--> <script setup> import HelloWorld f…...

【广州华锐互动】利用VR开展高压电缆运维实训,提供更加真实、安全的学习环境
VR高压电缆维护实训系统由广州华锐互动开发,应用于多家供电企业的员工培训中,该系统突破了传统培训的限制,为学员提供了更加真实、安全的学习环境,提高了培训效率和效果。 传统电缆井下运维培训通常是在实际井下环境中进行&#x…...
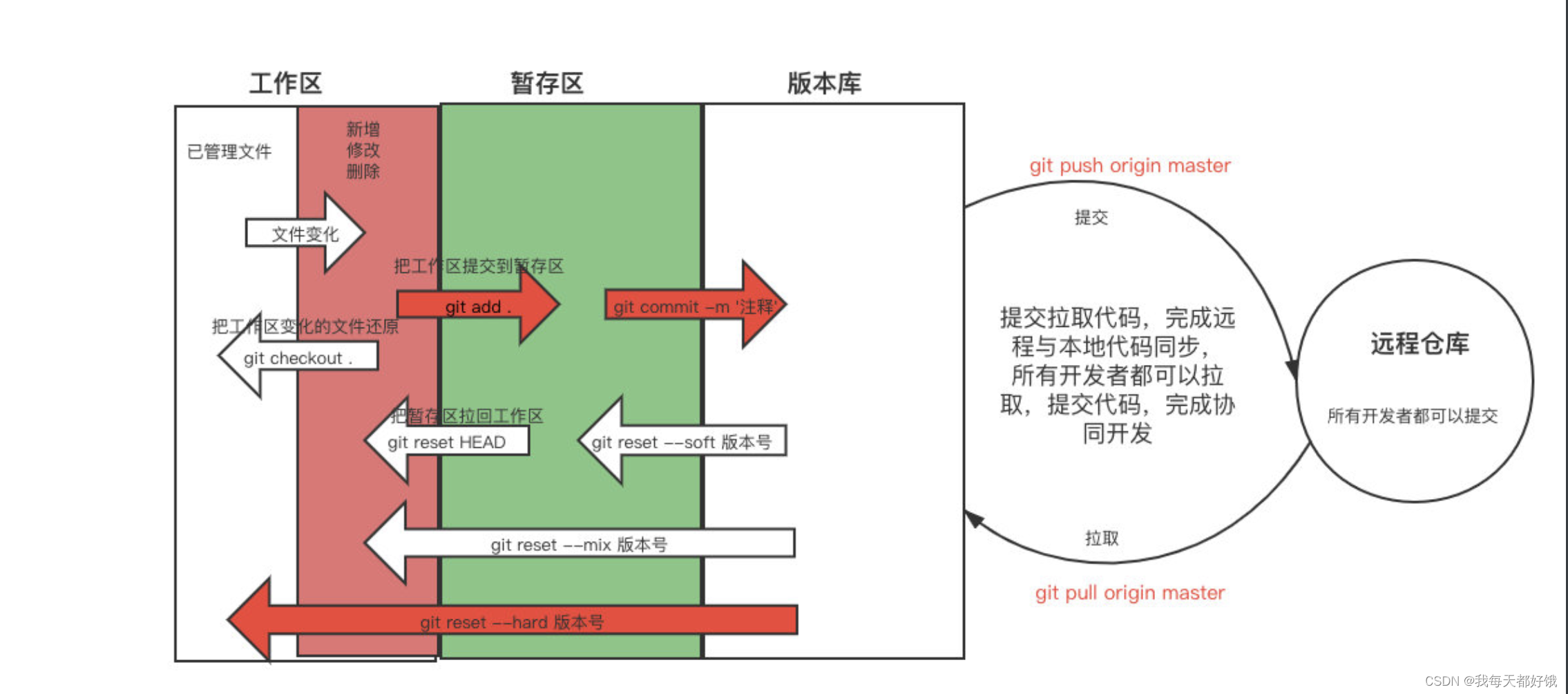
git的介绍和安装、常用命令、忽略文件、分支
git介绍和安装 首页功能写完了 ⇢ \dashrightarrow ⇢ 正常应该提交到版本仓库 ⇢ \dashrightarrow ⇢ 大家都能看到这个 ⇢ \dashrightarrow ⇢ 运维应该把现在这个项目部署到测试环境中 ⇢ \dashrightarrow ⇢ 测试开始测试 ⇢ \dashrightarrow ⇢ 客户可以看到目前做的…...
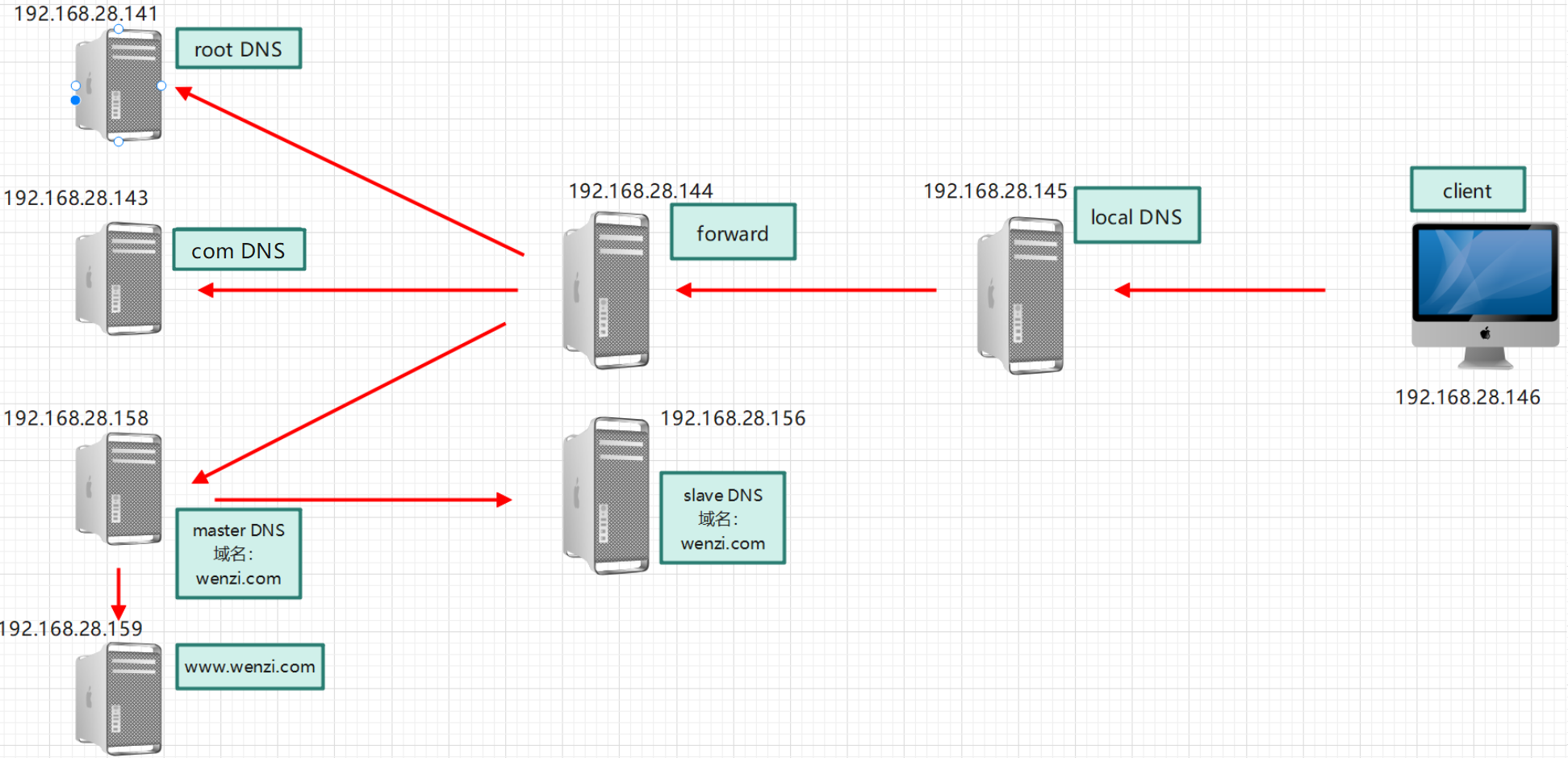
DNS(二)
实现 Internet DNS 架构 架构图 实验环境 关闭SELinux、Firewalld。时间保持一致 主机名IP角色client192.168.28.146DNS客户端,DNS地址为192.168.28.145localdns192.168.28.145本地DNS服务器(只缓存)forward192.168.28.144转发目标DNS服务…...
win 10怎么录屏?教你轻松捕捉屏幕活动
在当今科技快速发展的时代,录屏已成为信息分享、教学、游戏直播等方面的重要工具。无论是为了制作教程、分享游戏过程还是保存重要信息,录屏功能都发挥着举足轻重的作用。可是很多人不知道win 10怎么录屏,本文将详细介绍win10的三种常用录屏方…...
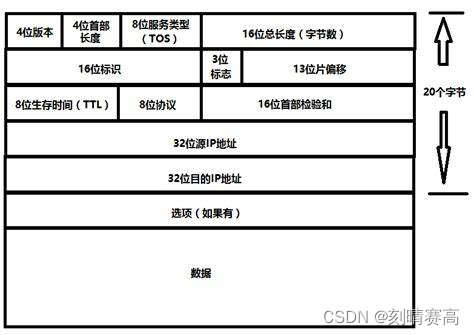
IP 协议的相关特性(部分)
IP 协议的报文格式 4位版本号: 用来表示IP协议的版本,现有的IP协议只有两个版本,IPv4,IPv6。 4位首部长度: 设定和TCP的首部长度一样 8位服务类型: (真正只有4位才有效果)…...

Java设计模式之代表模式
代表模式(Mediator Pattern)是一种行为型设计模式,它通过封装一组对象之间的交互方式,使得这些对象之间的通信变得松散耦合,从而降低了对象之间的直接依赖关系。代表模式通过引入一个中介者(Mediator&#…...
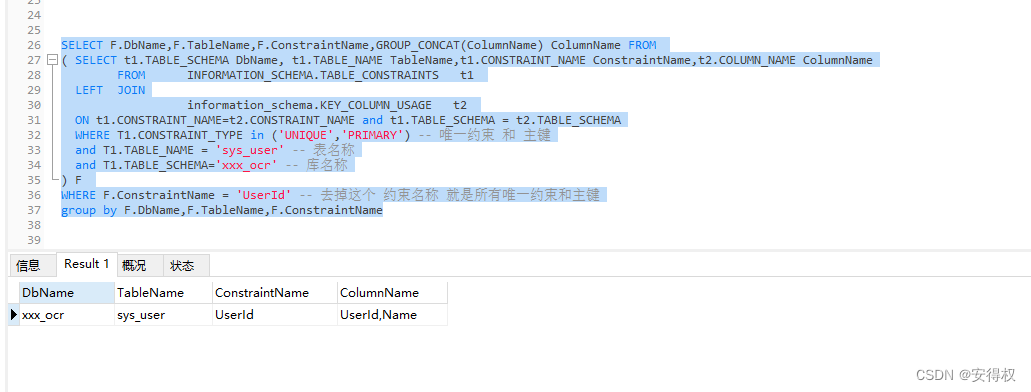
MySQL 查询 唯一约束 对应的字段,列名称合并
MySQL 查询 唯一约束 对应的字段,列名称合并 SELECT F.DbName,F.TableName,F.ConstraintName,GROUP_CONCAT(ColumnName) ColumnName FROM ( SELECT t1.TABLE_SCHEMA DbName, t1.TABLE_NAME TableName,t1.CONSTRAINT_NAME ConstraintName,t2.COLUMN_NAME ColumnNam…...
JDBC-day05(DAO及相关实现类)
七:DAO及相关实现类 1. DAO介绍 DAO:全称Data Access Object,是数据访问对象.在java服务器开发的三层架构中分成控制层(Controller),表示层(Service),数据访问层(Dao),数据访问层专门负责跟数据库进行数据交互.,包括了对数据的CRUDÿ…...

华为汪涛:5.5G时代UBB目标网,跃升数字生产力
[阿联酋,迪拜,2023年10月12日] 在2023全球超宽带高峰论坛上,华为常务董事、ICT基础设施业务管理委员会主任汪涛发表了“5.5G时代UBB目标网,跃升数字生产力”的主题发言,分享了超宽带产业的最新思考与实践,探…...
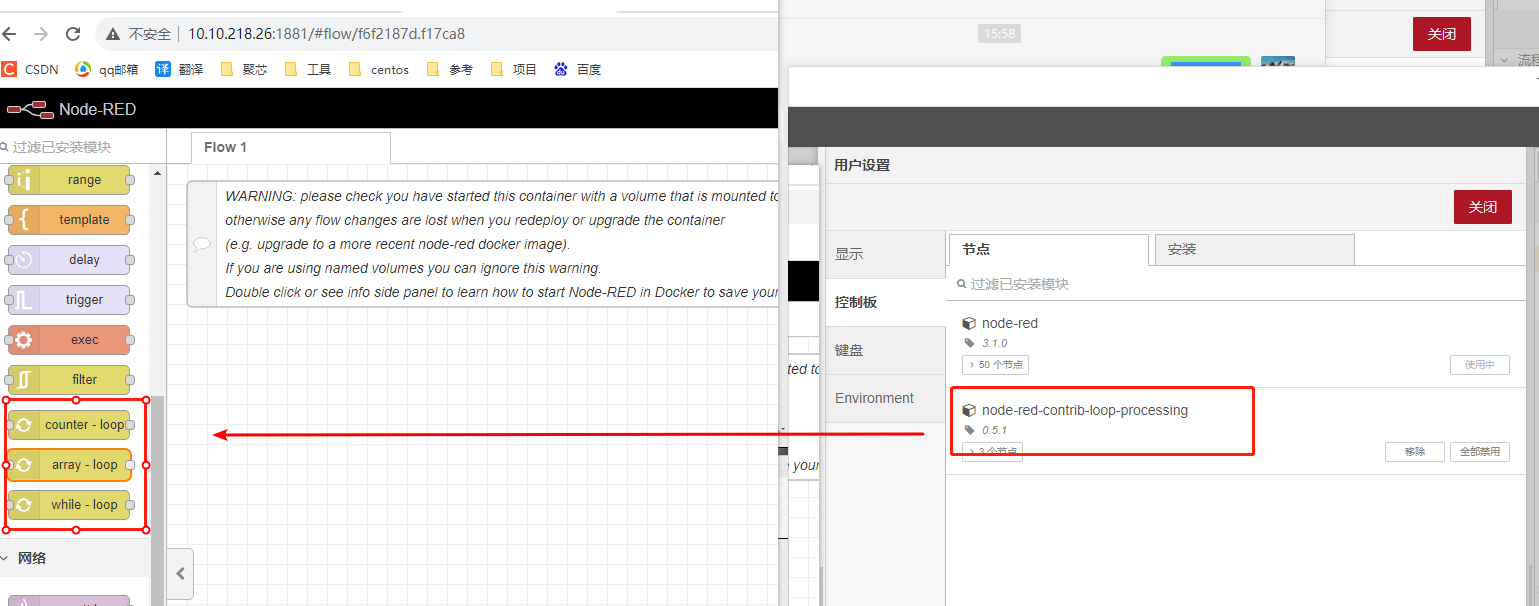
docker部署多个node-red操作过程
docker部署多个node-red操作过程 一、docker安装教程二、docker安装node-red2.1 在线安装node-red镜像2.1.1 拉取镜像2.1.2 创建目录并分配权限 2.2 离线安装node-red镜像 三、 docker操作node-red3.1 部署node-red3.2 查看\关闭\删除容器 四、Docker删除Redis镜像五、离线安装…...

王兴投资5G小基站
边缘计算社区获悉,近期深圳佳贤通信正式完成数亿元股权融资,本轮融资由美团龙珠领投。本轮融资资金主要用于技术研发、市场拓展等,将进一步巩固和扩大佳贤通信在5G小基站领域的技术及市场领先地位。 01 佳贤通信是什么样的公司? 深…...
】54 - /ifs/bin/startupmgr 程序工作流程分析 及 script.c 介绍)
【SA8295P 源码分析 (一)】54 - /ifs/bin/startupmgr 程序工作流程分析 及 script.c 介绍
【SA8295P 源码分析】54 - /ifs/bin/startupmgr 程序工作流程分析 及 script.c 介绍 一、startupmgr 可执行程序工作解析1. startupmgr\src\script.c 入口 main 函数:调用 init_loader_and_launcher 解析 scripts 数组二、ifsloader镜像加载流程分析:init_loader_and_launche…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

Opencv中的addweighted函数
一.addweighted函数作用 addweighted()是OpenCV库中用于图像处理的函数,主要功能是将两个输入图像(尺寸和类型相同)按照指定的权重进行加权叠加(图像融合),并添加一个标量值&#x…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

视频字幕质量评估的大规模细粒度基准
大家读完觉得有帮助记得关注和点赞!!! 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用,因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型(VLMs)在字幕生成方面…...